基于BP神經網絡的輪帶系統的變結構控制

程翔，張偉

(福州大學 機械工程及自動化學院，福建 福州 350108)

基于BP神經網絡的輪帶系統的變結構控制

程翔，張偉

(福州大學 機械工程及自動化學院，福建 福州 350108)

采用變結構離散指數趨近律設計出有效的控制律,通過控制張緊臂的狀態，從而抑制輪帶的橫向振動。運用BP神經網絡自適應調整控制律的參數，抑制了系統抖振問題。仿真結果表明，基于BP神經網絡離散指數趨近律的滑模控制律有效抑制了輪帶的橫向振動和系統在滑模面的抖振。

軸向運動弦線；變結構控制；離散指數趨近律；BP神經網絡

0 引言

輪帶系統在現代自動化工業中有著很廣泛的應用，如汽車發動機平帶驅動系統、高樓電梯纜繩、動力傳動帶等，但其振動卻限制了有效應用。因此有必要對其振動進行分析和控制。典型的輪帶系統包含有皮帶、滾輪和一個作動器。其中作動器由張緊臂和張緊輪組成，而皮帶因其抗彎剛度極小，可以模型化為一軸向運動弦線。

Ulsoy首次將模態控制應用于軸向運動弦線的橫向振動控制[1]。Ulsoy等[2]首次考慮了軸向運動弦線的橫向振動與張緊器的耦合振動。Beikmann[3]等學者最早提出了有著兩個滑輪和一個張緊裝置構成的典型模型，并證明輪帶系統的固有頻率與速度有關，弦線的橫向振動的模態與張緊臂狀態有關。Fung等[4]用Galerkin方法離散控制方程，用自變模型空間控制的變結構控制方法設計軸向運動弦線系統的控制規律。Fung等[5]研究了一升降機纜繩，采用變結構控制耦合振動。

現將作動器動力學方程離散化，運用神經網絡離散指數趨近律設計合適的控制器來控制張緊臂的轉動角度，通過對張緊臂的控制從而間接控制弦線的橫向振動，仿真驗證控制方法的有效性。

1 軸向運動弦線動力學方程

軸向運動弦線的模型如圖1所示，主要由一根弦線和一個作動器(張緊臂和張緊輪)組成。其中軸向運動弦線速度為c，單位密度為ρ，軸向張力為P。

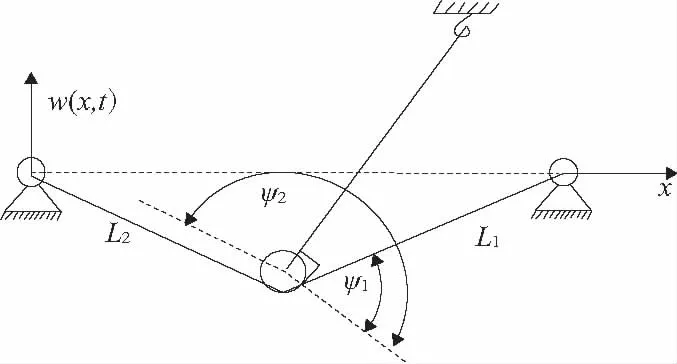
圖1 軸向運動弦線模型

為簡化模型，作以下假設：

1) 忽略系統各元件之間的阻尼；

2) 系統在運動中不打滑；

3) 忽略弦線的抗彎剛度。

運用Hamilton原理可推導出弦線和張緊器的動力學方程[6-7]：

(1)

邊界條件為：

(2)

作動器動力學方程：

(3)

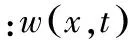
(4)

將式(4)代入弦線運動方程式(1)中，消去eiωt后可得：

(5)

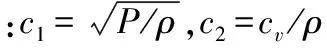
解二階復系數齊次線性微分方程[8]式(5)可得：

(6)

其中：

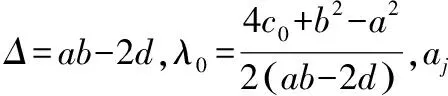
聯立方程式(1)、式(2)、式(4)和式(6)，可得弦線橫向振動位移：

(7)

聯立方程式(2)和式(7)，則容易得到：

(8)

作動器動力學方程可化為：

(9)

其中：

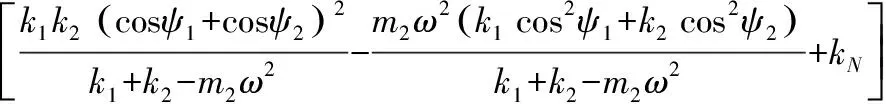
(10)

2 控制器設計

變結構控制對系統攝動及外部干擾有較好的魯棒性，且具有快速響應、無需系統在線辨識、物理實現簡單等優點，是一種易于實現的綜合控制方法。而隨著計算機技術的高速發展和工業自動化等領域的實際需要，控制算法的實現經常采用數字計算機，但當采用數字計算機實現變結構控制算法時，由于采樣過程的限制，理想的滑動模態不存在，狀態軌跡以抖動形式沿著滑平面運動。因此，研究離散時間系統變結構控制方法具有重要的理論價值和實際意義。

人工神經網絡具有較強的學習能力和高度的并行運算能力，能充分逼近任意復雜的非線性關系并具有較強的魯棒性和容錯性。神經網絡和滑模變結構控制相結合，可以使得系統在保持對攝動和外部干擾強魯棒性的同時盡量消除抖振。

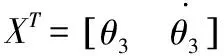
(11)

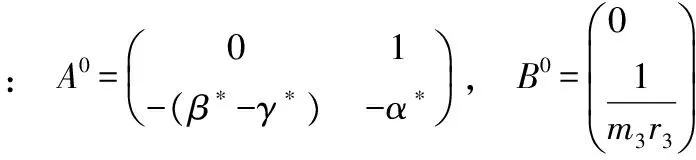
(12)

采樣周期T=0.01，方程離散化可得：

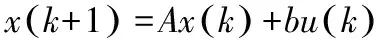
(13)

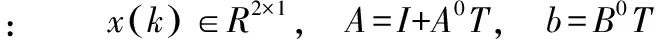
(14)

對于離散指數趨近律[9-10]：

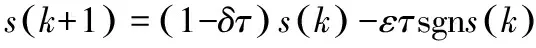
(15)

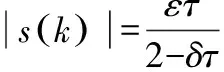
采用3-m-1的3層BP神經網絡來實現參數ε和δ的實時估計，其結構如圖2所示。其中wij表示網絡輸入層第i個節點(i=1,2,3)到隱含層第j個節點(j=1,2,…,m)的連接權值；wj表示隱含層第j個節點到輸出節點的連接權值。則網絡對ε輸出：

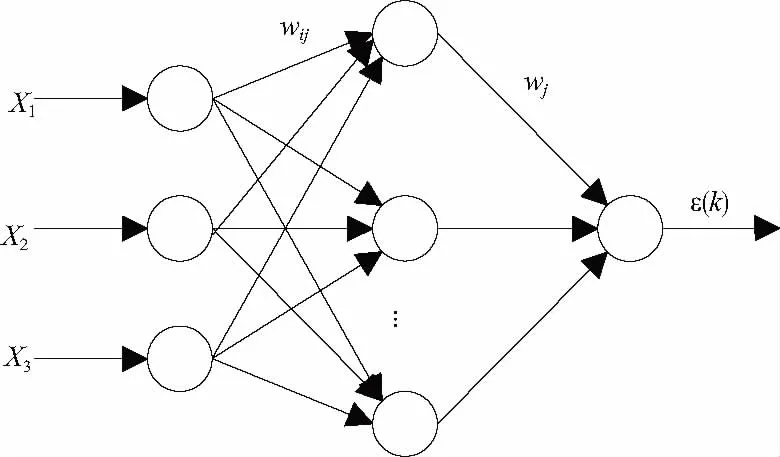
圖2 神經網絡結構圖

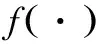
則神經網絡指數趨近律可表示為:

(16)

針對式(9)的離散時間系統，定義滑模切換函數：

(17)

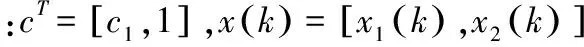
(18)

基于神經網絡指數趨近律式(15)，由式(13)和式(17)可得神經網絡滑模變結構控制器：

(19)

由于ε>0，0<δ<1/τ,所以網絡輸出層神經元激勵函數取sigmoid函數。采用系統狀態變量和控制變量作為網絡的輸入矢量，即設:

則神經網絡輸出分別為：

(20)

(21)

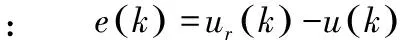
(22)

根據梯度下降法，由式(19)-式(22)，可得附加動量項的權值修改公式：

(23)

其中：0<η<1為學習速率，0<α<1為動量系數。

3 數值仿真

圖3中可以看出切換函數s快速趨近于0，且抖振很小，表明該控制律有效的改善了變結構控制系統的動態性能。通過比較圖4與圖5中未控系統和受控系統的角位

移和橫向振動可知，文中的控制律有效的抑制了軸線運動弦線的橫向振動。

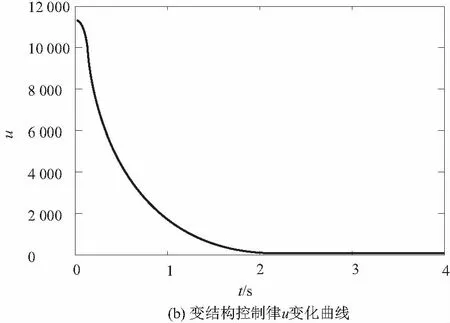
圖3 變化曲線

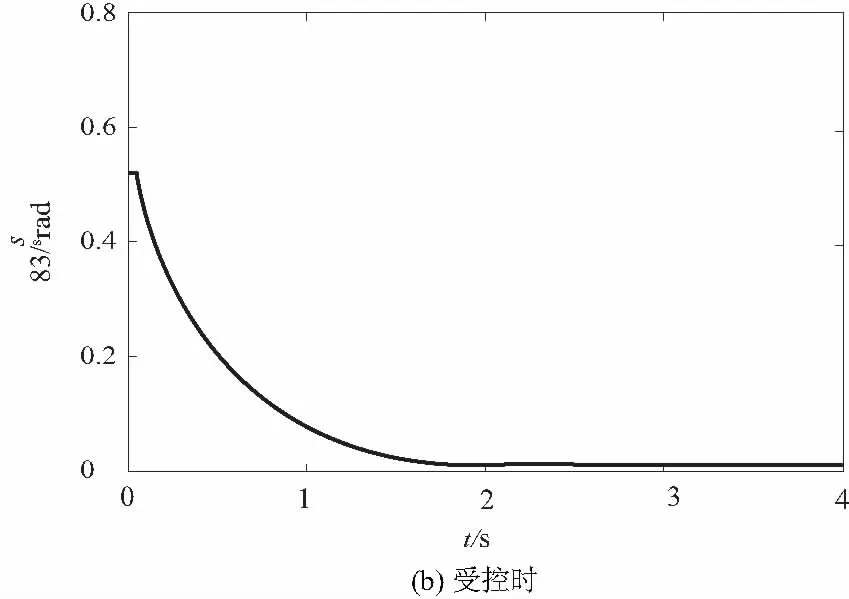
圖4 張緊臂角位移變化曲線

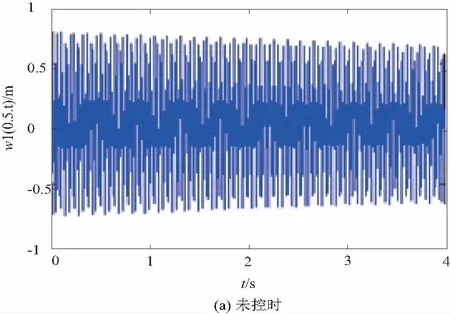
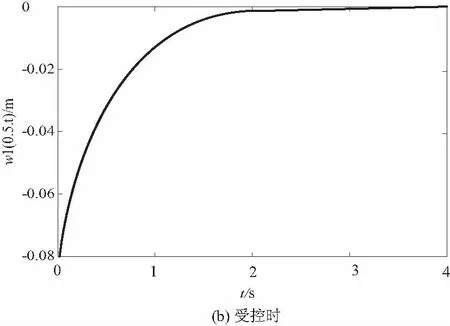
圖5 x=0.5處弦線的橫向振動位移

4 結語

結合輪帶系統的橫向振動與張緊臂角位移相耦合的動力學方程，通過神經網絡控制，自適應調整離散指數趨近律參數，設計的變結構控制器有效地抑制了張緊臂角位移的變化，從而達到抑制輪帶系統橫向振動的目的。變結構控制系統的抖振較小，動態品質和魯棒性能良好。文中所采用的離散方法物理上易于實現，張緊臂的角位移與角速度可通過傳感器測出。仿真結果驗證了控制律的有效性。

[1] A. Galip Ulsoy. Vibration Control in Rotating or Translating Elastic Systems[J]. Journal of Dynamic Systems, Measurement and control, 1984,106(1):6-14.

[2] A. G. Ulsoy,J. E. Whitesell,M. D. Hooven. Design of Belt-Tensioner Systems for Dynamic Stability[J]. Journal of Vibration and acoustics,1985, 107(3):282-290.

[3] Beikmann, R.S.Perkins, N.C. Free vibration of serpentine belt drive systems[J]. Journal of Vibration and Acoustics, 1996, 118(3):406-406.

[4] Rong-Fong Fung and Cheng-Chan Liao. Application of variable structure control in the nonlinear string system[J]. International journal of Mechanical Sciences, 1995, 37(9):985-993.

[5] Fung RF,Yao CM.Lin JH. VIBRATION ANALYSIS AND SUPPRESSION CONTROL OF AN ELEVATOR STRING ACTUATED BY A PM SYNCHRONOUS SERVO MOTOR[J]. Journal of Sound and Vibration, 1997, 206(3):399-423.

[6] Zhang L,Zu J W. Model analysis of serpentine belt drive systems[J]. Journal of Sound and Vibration,1999,222(2):259-279 .

[7] 余小剛，張偉. 軸向運動弦線橫向振動的變結構控制[J]. 福州大學學報(自然科學版)，2012，(2)：72-75.

[8] 湯光宋，甘欣榮. 復系數復數方程的求根及復系數常微分方程的通解公式[J]. 江漢大學學報，1996，13(3):80-82.

[9] 高為炳. 離散時間系統的變結構控制[J]. 自動化學報，1995，21(2)：154-160.

[10] 陳志梅，王貞艷，張井岡. 滑模變結構控制理論與應用[M]. 北京：電子工業出版社，2012.

Variable Structure Control of Belt Drive Systems via BP Neural Network Methods

CHENG Xiang,ZHANG Wei

(College of Mechanical Engineering and Automation，Fuzhou University，Fuzhou 350108，China)

in order to control the state of the tension arm, a discrete index reaching law of the variable structure is used to design an effective sliding mode control law. As a result, the transverse vibration of the belt is restrained. By using BP neural network methods, the chattering of the variable structure is controlled. Simulation results show that the chattering and the transverse vibration of the belt are well suppressed by the sliding mode control law.

axially moving string; variable structure control; discrete index reaching law; BP neural network

福州大學科研啟動基金資助項目(826230)；福州大學科技發展基金資助項目(826807)

程翔(1989-)，男，湖北宜昌人，碩士研究生，研究方向為機械振動與控制。

O321

B

1671-5276(2015)05-0176-04

2014-03-18