噴嘴結構對水射流性能影響的分析

李俊, 張慶，周一睜

(南京理工大學,江蘇 南京 210094)

噴嘴結構對水射流性能影響的分析

李俊, 張慶，周一睜

(南京理工大學,江蘇 南京 210094)

介紹了水射流理論及其計算流體力學的數學模型，運用FLUENT軟件對不同結構噴嘴的水射流流場進行仿真分析。通過仿真結果比較得出：錐直形噴嘴整流段長度對噴射速度具有一定影響，且有利于噴嘴出口流量的增加；當噴嘴收縮角為14°時，水射流性能最佳。

水射流；噴嘴結構；流場仿真

0 序言

隨著計算機和流體數值技術的快速發展以及許多湍流模型的成功建立，應用數值模擬的方法對水射流流動特性和物理量的分布規律進行研究具有更準確、可靠、迅速的優點。從20世紀30年代起，人們就利用理論，實驗等多種手段對水射流進行了廣泛的研究，而噴嘴是形成水射流的直接元件，其作用是將水的壓力能轉化為動能，因此噴嘴的結構直接決定著水射流的性能[1]。

1 水射流理論介紹

目前對于水射流已經形成了一套比較完整的分析方法。工程所用的水射流絕大數是湍流流動，其實際整體結構相當復雜，為了便于分析，眾多學者將射流過程分為初始段、基本段、和耗散段3個階段[2]。

初始段是射流的核心段，水流一離開噴嘴就與空氣發生劇烈的動量交換和紊動擴散，但中心線附近的水射流在初始段仍保持噴嘴出口初始速度。初始段長度決定了水射流噴射的距離。

基本段是水射流的主體段，在這個階段絕大部分為充分發展的紊動混摻區，且段內射流的軸向流速和動壓力逐漸減少。

消散段也稱為水射流的霧化段，此時射流已經變成水滴與空氣的混合物或已霧化，軸向速度與動壓力相對較低。

2 建立水射流數學模型

由于文中研究的是自由非淹沒紊動射流，考慮水的粘性，且認為水射流過程中水流是不可壓的。則在空間直角坐標系中，對于不可壓流體，水射流連續方程為：

在空間直角坐標系中，對于不可壓流體的N-S方程為[3]：

直接求解上述瞬態的控制方程難度很大，則采用時間平均處理的方法，從而引入了雷諾方程，雷諾方程相比N-S方程多了應力項，稱為雷諾應力，此時形成的方程組不封閉，必須使用新的湍流模型使方程封閉，因此引入湍動能方程和湍流耗散率方程，便形成了不可壓縮流體的標準k-ε模型[4]：

Gk+Gb-ρε-YM+Sk

其中：湍流粘度μt=ρCμk/ε，Gk為由平均速度梯度引起的湍動能的產生項；Gb為由浮力引起的湍動能的產生項；YM代表可壓湍流中脈動擴張的貢獻；C1ε、C2ε、C3ε為經驗公式，σk和σε分別為與湍動能和耗散率對應的Prandtl數；Sk和Sε是用戶定義的源項。

水射流基本方程由連續方程，雷諾方程和標準k-ε方程共同組成。

3 噴嘴的選擇

噴嘴是形成水射流的核心部件。噴嘴結構主要指噴嘴的長徑比、收縮角和流道形狀[5]。不同結構的噴嘴所形成的流量系數，射流的擴散角和等速核長度都不相同。噴嘴的流道形狀有橢圓形、流線型、圓弧型和錐形等，這些噴嘴的水力特性如表1。綜合考慮噴嘴性能和加工，常使用錐形噴嘴，因此文中選擇錐形噴嘴進行研究。當錐形噴嘴的收縮角取較大值時，在減小流體在噴嘴入口處的阻力的同時，也會使流動得不到充分發展，最終影響水射流的性能；當收縮角取值小時，又將給流動帶來過大阻力。而錐直型噴嘴的整流段可改善流體從噴嘴中噴出前的狀態，使噴出后的射流在空氣中更穩定。

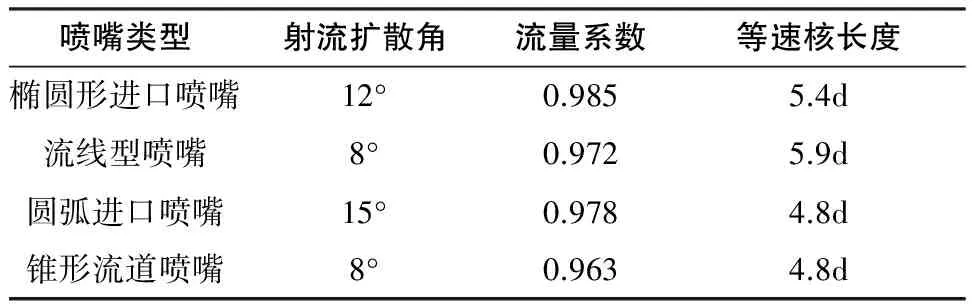
表1 各種噴嘴的水力特性對比

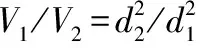
4 噴嘴射流流場仿真

4.1 幾何建模與網格劃分

直接運用ICEM對二維噴嘴水射流流場建模并進行網格劃分。采用結構化網格劃分，因為結構化網格比非結構化網格更容易收斂，計算速度更快，也更準確。以d型噴嘴為例，網格劃分后的結果如圖1所示。

圖1 d型噴嘴的網格劃分

4.2 模型選擇與邊界條件確定

文中考慮的屬于非淹沒自由水射流，噴射出的水在空氣中運動并與空氣發生劇烈的能量傳遞和動量交換，因此采用氣液兩相流模型[8]。根據雷諾數求解公式Re=vdH/υ，可得水射流運動狀態為湍流，因此采用標準的k-ε模型。

設置計算域邊界條件，取d型噴嘴的射流流場計算域為例，如圖2所示，其中邊A設置為速度入口，將第二相水的體積分數設置為1，表示入口充滿水；邊B設置為自由出口；CDEC1D1E1設置為固體壁面，采用FLUENT中默認的無滑移條件，且對近壁處的流體應用近壁函數。二維水射流流場參數尺寸分別為：噴嘴入口長度為20 mm，噴嘴出口長度為10 mm，噴嘴入口速度為1 m/s。

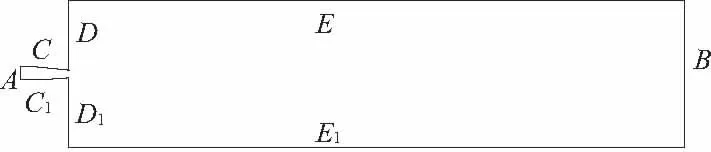
圖2 二維噴嘴水射流流場

4.3 仿真結果及其分析

分別對上述4種噴嘴進行水射流流場仿真，結果如圖3所示。

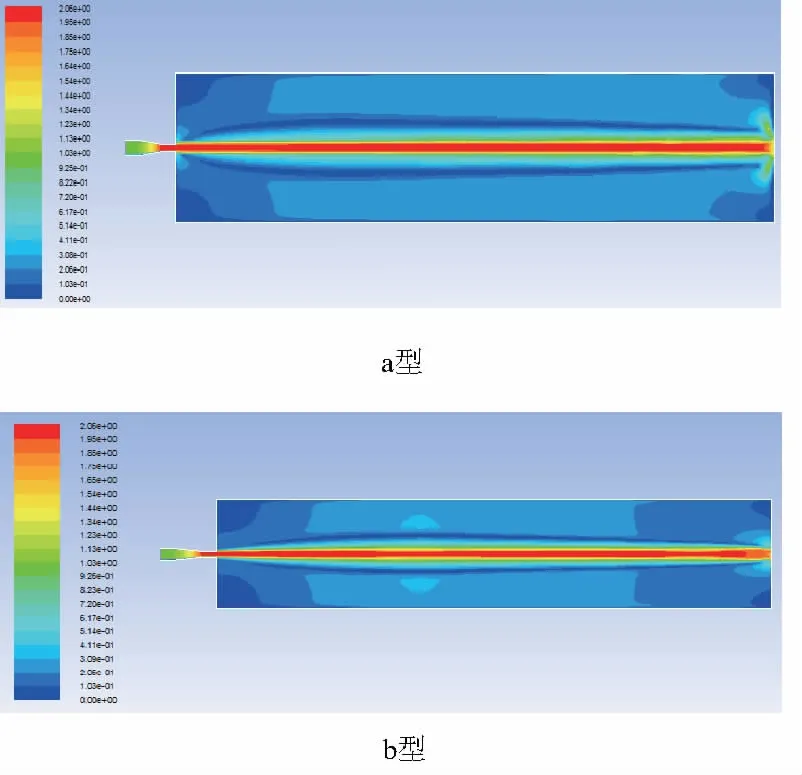
圖3 噴嘴水射流流場速度云圖

由圖3可得水流從噴嘴中噴出后的速度均為2m/s左右，而根據連續性方程可知，噴嘴出口的速度為2m/s，仿真出的結果與理論公式求解出的結果近似相等。

當錐直形噴嘴的收縮角不同時，噴嘴出口速度和噴嘴出口靜壓會發生變化，其關系分別如圖4和圖5所示。

圖4 噴嘴收縮角對噴嘴出口速度的影響

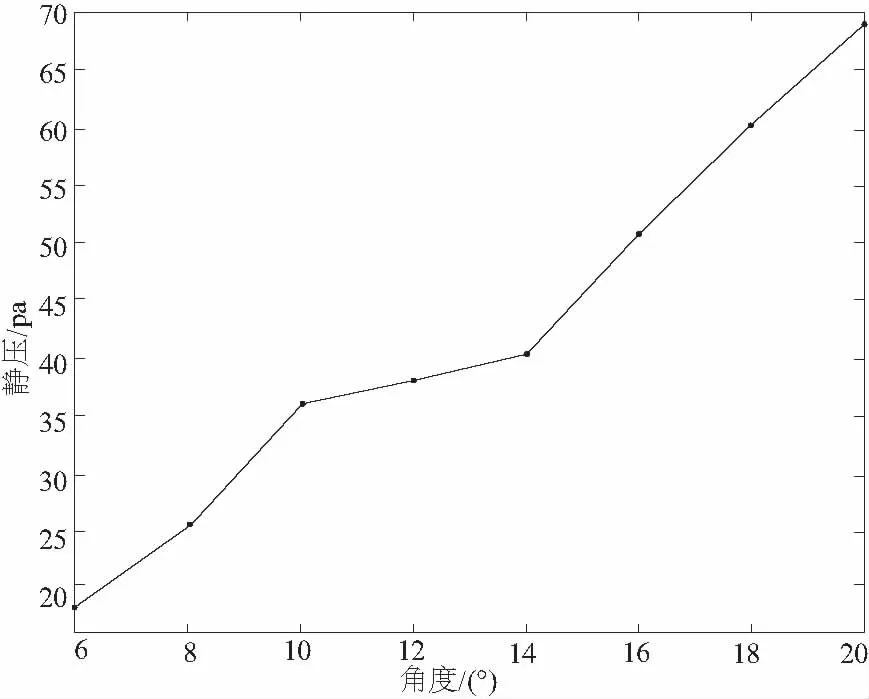
圖5 噴嘴收縮角對噴嘴出口靜壓的影響

比較a型和b型噴嘴水射流流場的仿真結果可得：a型噴嘴內部流場相比b型的更紊亂；b型噴嘴整流段內的流體也比a型噴嘴的平緩。比較c型和b型噴嘴水射流流場的靜壓，發現收縮角為8°的噴嘴在出口處靜壓要小于收縮角為14°的噴嘴。這很好地證明了理論，即收縮角越小在收縮斷面形成的阻力就越大，從而導致能量耗散的增加，根據能量守恒定律，流體能量的耗散主要體現在靜壓的變化上。綜合考慮噴嘴出口速度與靜壓的影響，通過圖4和圖5得到：收縮角為14°的噴嘴對水射流性能提高更有利。

當錐直型噴嘴的長徑比不同時，噴嘴出口速度不同，通過仿真得到其關系如圖6所示。

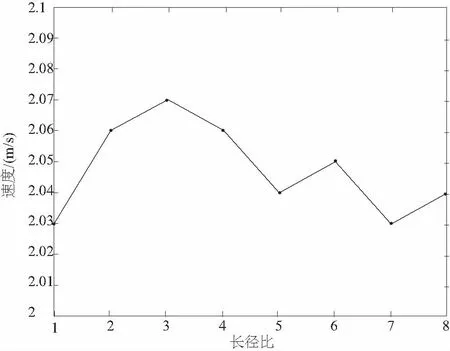
圖6 噴嘴長徑比對噴嘴出口速度的影響

比較b型和d型噴嘴形成的水射流流場，有整流段的噴嘴出口速度與沒有整流段的大致相同，但從b型噴嘴中噴射出的水流更加平穩。經過大量仿真得到圖6所示規律，則當長徑比為2～4時，噴嘴出口的速度最大。在噴嘴直徑變化處，由于水流流線不能夠轉折，射流會發生收縮，但射流在受到阻力后要發生擴散。當有適當長度的整流段時，擴散的射流就會發生附壁，在離開噴嘴前，液體已充滿整個截面，即收縮斷面發生在噴嘴的整流段內部，使噴嘴的截面收縮系數ε=1。同時收縮斷面處存在一定的真空度，因此對于錐直型噴嘴形成的水射流，不僅有動壓的驅動作用，而且還有真空抽吸作用，從而使出口流量有所增加，即具有整流段的噴嘴噴射出的水流流量一定大于沒有整流段時的流量。但當收縮斷面上的絕對壓力低于當地的飽和蒸汽壓力時，水流又將會在流過該截面處發生氣化，應避免出現這種情況。

5 結語

1) 選用FLUENT中的vof模型和標準的k-ε模型對不同結構噴嘴進行水射流流場仿真，仿真出的結果與理論值相似。

2)不同噴嘴結構對水射流性能具有較大影響。對于錐直形噴嘴而言，當收縮角為14°且噴嘴長徑比為2～4時，水射流性能最好。

[1] 魏德軍，曹仲文，李萍. 噴嘴形狀對噴射能力的影響[J]. 遼寧化工，2006，35(7)：416-418.

[2] 薛勝雄. 高壓水射流技術工程[M]. 合肥：合肥工業大學出版社，2006.

[3] 楊友勝，張建平，聶松林. 水射流噴嘴能量損失研究[J]. 機械工程學報，2013，49(2)：139-144.

[4] 劉沛清. 自由紊動射流理論[M]. 北京：北京航空航天大學出版社，2007.

[5] 裴二榮，柴金城. 噴嘴水力性能分析及設計[J]. 排灌機械，2004，22(5)：29-31.

[6] 孫德志，楊周，劉煒麗，等. 基于FLUENT的不同噴嘴輪廓線形對流出系數影響分析[J]. 理論與實驗，2007(12)：3-6.

[7] 王福軍. 計算流體動力學分析—CFD軟件原理與應用[M]. 北京：清華大學出版社，2005.

[8] 羅惕乾. 流體力學[M]. 北京：機械工業出版社，2007.

Analysis of Influence of Nozzle Convergence on Water-jet Capacity

LI Jun, ZHANG Qing，ZHOU Yizheng

(Nanjing University of Science and Technology, Nanjing 210094，China)

This paper introduces the theory of water-jet and mathematical model of its computational fluid dynamics and uses FLUENT solfware to simulate and analyae the water-jet flow fields with different nozzles. According to the compared result of the simulation，the rectifying section of nozzle not only has influences on the water-jet velocity, but also prompts the increase of the nozzle outlet flow. When the convergence angle of the nozzles is 14 degree, the performance of the water-jet is the best.

water jet; nozzle configuration; flow field simulation

李俊(1990-)，男，江蘇揚州人，碩士研究生，研究方向為機械設計。

TP391.9

B

1671-5276(2015)05-0102-03

2014-03-04