基于EOQ 下我國航材存儲模型的實例研究

蘇 濤，曹文靜，趙 敏

(海軍航空工程學院 a.控制工程系; b.研究生管理大隊，山東煙臺 264001)

人們在生產和日常生活中往往將所需的物資、用品和事物暫時的儲存起來，以備將來使用或消費。這種儲存物品的現象是為了解決供應(生產)與需求(消費)之間的不協調的一種措施，若是航材需求與供應、消耗與存儲之間存在著不協調性，其結果會產生2 種情況:一是供過于求，由于航材的積壓，造成航材保障經費的大幅增加和過期航材的報廢;二是供不應求，航空裝備完好率得不到有效保證，以此為研究對象，利用運籌學方法去解決最合理、最經濟的儲存問題。

1 傳統EOQ 模型的單一性與局限性

目前各航空公司多使用簡單EOQ 模型(如圖1 所示)來制訂采購計劃。此模型的運用基于下面的假設:

1)需求量是常量，反復出現并且是已知的;

2)準備時間是常量，也是已知的;

3)不允許缺貨。因為需求和準備時間是常量，人們可以準確地確定訂貨時間來避免缺貨;

4)訂貨或生產都是批量進行的，并且整個批量同時到達倉庫進行存儲;

5)使用的成本結構如下所示:貨物成本是固定的，對大批量的購買也沒有折扣。倉儲成本是由存儲平均水平線性地決定的。每批的訂貨成本是固定的，它與每批貨物的數量無關;

6)貨物是單一產品，和其他產品不發生相互作用。

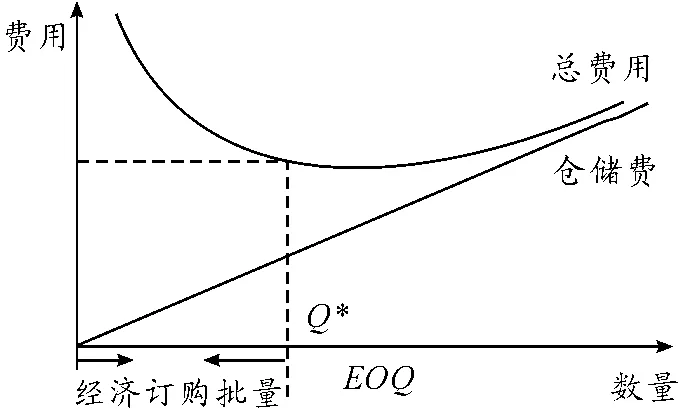
圖1 航材年倉儲費、訂購費和總費用曲線

Q*為在以上各條假設的基礎上，訂貨成本、倉儲成本之和最低時的訂貨批量。考慮到航材本身的實際特點，無法滿足以上各條假設，因此需要對簡單EOQ 模型進行修正。

在上述假設條件下，存貨的相關成本包括以下2 項:

1)訂貨成本。訂貨成本是指為組織進貨所發生的各種費用，包括采購人員的差旅費、通訊費、運輸費、檢查費等、這些費用一般與訂貨的次數有關。在存貨的全年需求量一定的情況下，一次訂貨量最多，全年的訂貨次數越少，訂貨費用越低。

2)存儲成本。存儲成本是指企業為持有存貨而發生的費用，包括存貨資金占用費用或機會成本、倉儲費用、存貸保險費用等。這些費用一般與平均存貨水平的高低成正比。在存貨的全年需求量一定的情況下，一次訂貨量越多，全年的平均存貨水平越高，存儲費用越高。

2 存儲數學模型的建立與求解

2.1 不允許缺貨的成批供應模型(EOQ 模型)

不允許缺貨，即設定缺貨損失費為無窮大。設存儲系統的輸出是連續均勻的，需求量為常數(單位時間的需求量為λ、年需求量為D);當存儲降到零時可以在提前訂貨時間T內得到補充，不會產生缺貨現象;提前訂貨時間T 固定不變，所訂購器材可以一次成批到達，存儲量變化如圖2 所示。

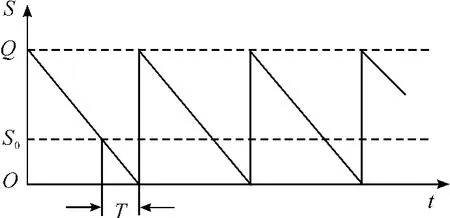
圖2 不允許缺貨的成批供應模型存儲量變化曲線

圖2中S0為訂貨點，即存儲量下降至S0時提前訂貨，S0=λT。

全年的存儲管理費為訂貨費與存儲費之和，即

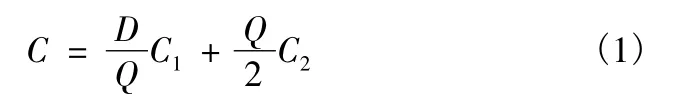
式中:Q 為訂貨量;D/Q 為全年訂貨次數;C1為每次訂貨費;Q/2 為平均存儲量;C2為單位器材的平均存儲量。

計算得，使全年存儲管理費最少的最佳訂貨量為

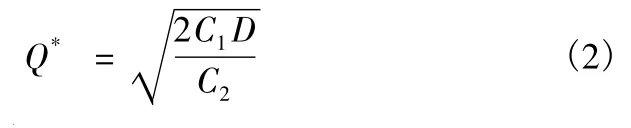
全年最少存儲管理費為

全年最佳訂貨次數為

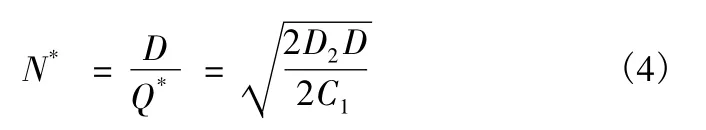
2.2 不允許缺貨的分批供應模型

不允許缺貨的成批供應模型適用于所訂購器材可以一次成批到達。由于生產或運輸等多方面原因，所訂購器材多數是逐次分批到達的，其存儲是邊補充邊陸續消耗的，存儲量變化如圖3 所示。

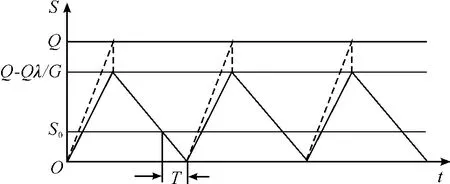
圖3 不允許缺貨的分批供應模型

圖3中，G 為到貨率，即單位時間內的到貨量;Q -Qλ/G為量大存儲量。

由于存儲量上升率與下降率均為線性，得平均存儲量為

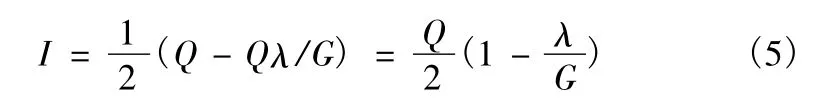
全年存儲費為

全年存儲管理費為

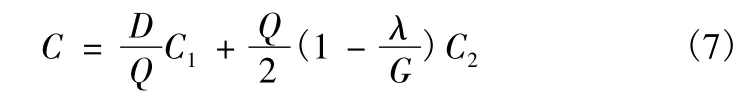
計算得使全年存儲管理費最少的最佳訂貨量為

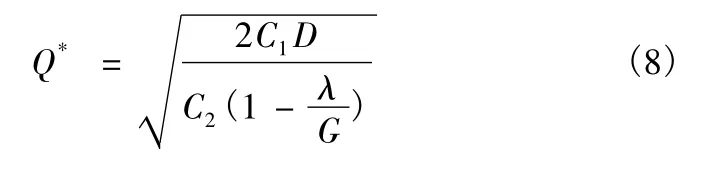
全年最少存儲管理費為

全年最佳訂貨次數為

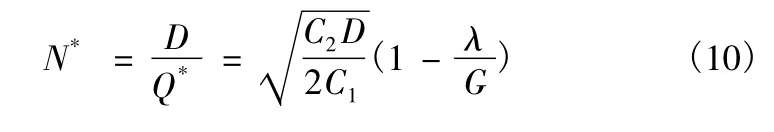
3 擴展的允許缺貨供應模型

3.1 允許缺貨的成批供應模型

允許缺貨的成批供應模型是不允許缺貨的成批供應模型的基礎上，在存儲管理總費用中加入了缺貨損失費，其存儲量變化如圖4 所示。

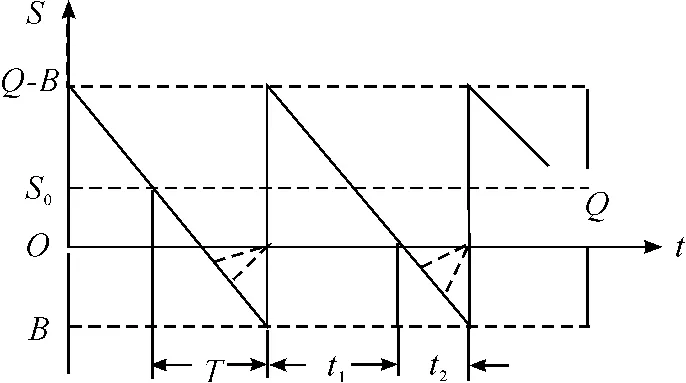
圖4 允許缺貨的成批供應模型存儲量變化曲線

圖4中:t1為存儲有貨時間;t2為允許供應缺貨時間;B為允許缺貨量;Q-B 為最大存儲量。全年存儲管理費為

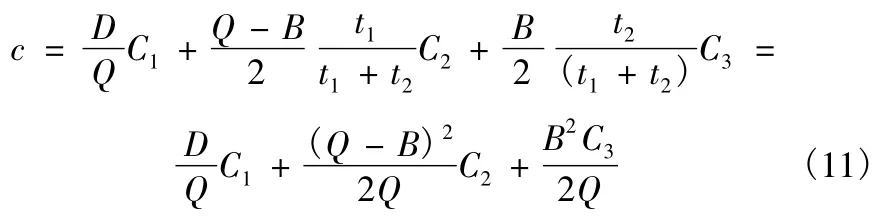
計算得，使全年存儲管理費最少的最佳訂貨量為

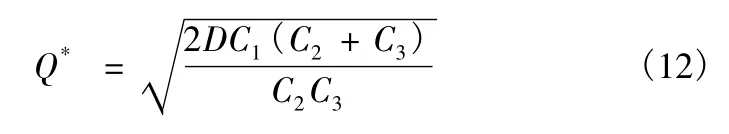
全年最少存儲管理費為

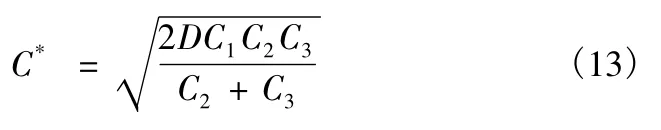
全年最佳訂貨次數為

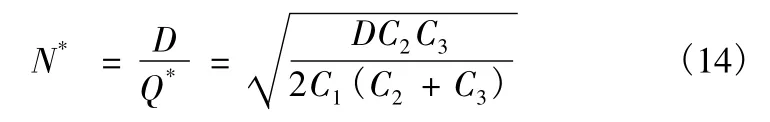
比較允許缺貨的成批供應模型和不允許缺貨的成批供應模型，允許缺貨的成批供應比不允許缺貨的成批供應的最佳訂貨量增加了倍，全年最佳訂貨次數和最少存儲管理費均下降了倍。

3.2 允許缺貨的分批供應模型

允許缺貨的分批供應模型，其存儲量變化如圖5 所示。

圖5 允許缺貨的分批供應模型存儲量變化曲線

圖5中:t1為存儲量從0 增加到全部到貨(存儲量最大)所需時間;t2為存儲量從最大值下降到0 所需時間;t3為存儲量為0 到訂貨開始到達所需時間;t4為從訂貨開始到達至補夠缺貨所需的時間;Q-B 無實際物理意義;Q-B-(t1+t4)λ為最大存儲量。

建立模型，解得使全年存儲管理費最少的最佳訂貨量為

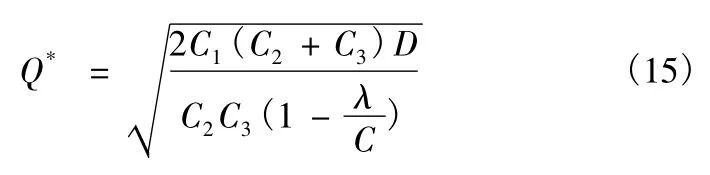
全年最少存儲管理費為

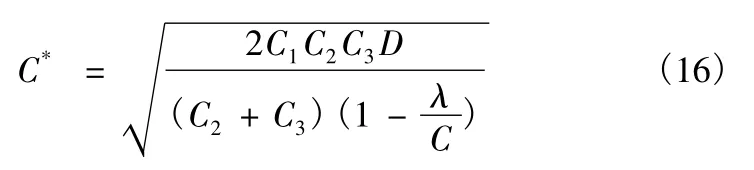
全年最佳訂貨次數為

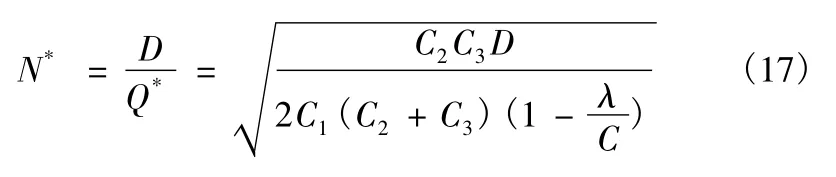
比較允許缺貨的分批供應模型和不允許缺貨的分批供應模型，允許缺貨的分批供應比不允許缺貨的分批供應的最佳訂貨量增加了倍，全年最佳訂貨次數和最少存儲管理費均下降了倍。

4 實例求解

1)例1 設某部每天所需要的某型航材量是相同的，每年需要1 000 kg，每年該型器材的存儲費為5 元/kg，每次外出訂貨需要訂貨費100 元，若每次訂貨數量不限，訂貨后能夠在存儲量為零時一次成批到貨，怎樣組織訂貨才能使該型航材的存儲管理費最少。

根據題意，已知D=1 000，C1=100，C2=5，計算得，最佳訂貨量為

全年最佳訂貨次數為

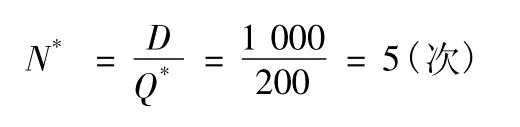
全年最少存儲管理費為

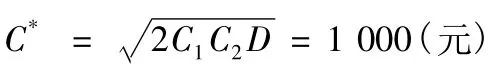
2)例2 承例1，若訂購航材為陸續到達，每天到貨量為30 kg，試求最佳訂貨量Q*。

根據題意，已知D =1 000，C1=100，C2=5，λ =1 000/365≈2.74(每年按365 天計算)，G =30，計算得，最佳訂貨量為

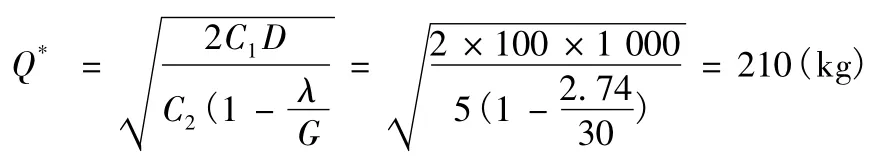
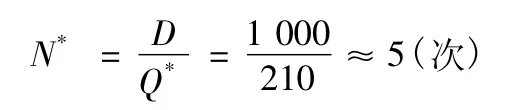
全年最佳訂貨次數為全年最少存儲管理費為

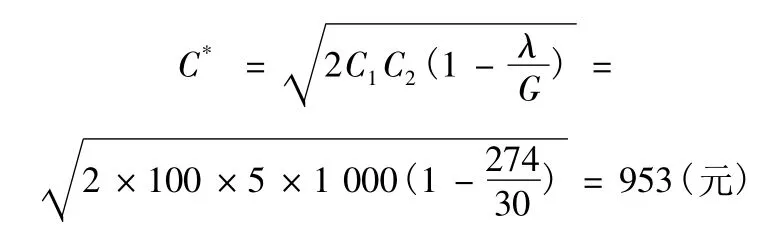
3)承例1，若訂購航材允許缺貨，可在下批貨到時補上，但缺貨損失為每年每件損失費為100。根據式(12)、式(13)、式(14)可以得到:

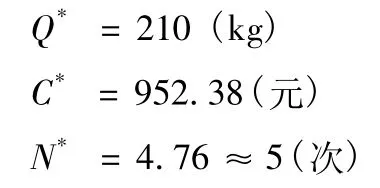
4)承例2，若訂購航材允許缺貨，可在生產需要一定時間情況下，缺貨損失費為每年每件損失費為100。根據式(15)、式(16)、式(17)可以得到:

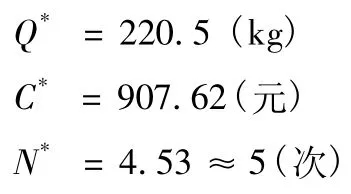
5 結果分析

1)通過以上對比研究可以得出，分批供應要比成批供應節省存儲管理費，但是分批供應一般會增加庫存管理工作量。允許缺貨條件下的模型比不允許缺貨條件下的模型的最佳訂貨量增加了倍，全年最佳訂貨次數和最少存儲管理費均下降了倍。

2)建立的模型是確定性的，即一個周期內的需求量是已知的。如果不是這樣的話，更合適的模型將是隨機的(或概率的)，也就是一個周期內的需求量是一個已知分布的隨機變量。

3)本文不僅考察了基本經濟批量模型的確定型庫存問題的研究，對EOQ 模型的進一步擴展也有所展開，比如允許缺貨條件下的分批供應模型和允許缺貨條件下的成批供應模型等，對有效降低總的存儲費用有較好的研究價值。

［1］韓伯棠.管理運籌學［M］.北京:高等教育出版社，2003.

［2］魏國華，傅家良，周仲良.實用運籌學［M］.北京:清華大學出版社，2000.

［3］胡運權，郭耀煌.運籌學教程［M］.北京:清華大學出版社，2002.

［4］鄧成梁.運籌學的原理和方法［M］.2 版.武漢:華中科技大學出版社，2002.

［5］余興無，李旭東.確定性存儲基本模型的幾個推廣［J］.甘肅科學學報，2002(02):76- 79.

［6］陳曉芳，岳才保.動態存儲模型研究［J］.武漢理工大學學報，2003(01):88- 91.

［7］胡運權，郭耀煌.運籌學教程［M］.北京:清華大學出版社，2003.

［8］姜啟源，謝金星，葉俊.數學模型［M］.北京:高等教育出版社，2003.

［9］杜廷松.訂貨問題的一個最優存儲模型［J］.商場現代化，2007.

［10］趙經成，祝華遠，王文秀.航空裝備技術保障運籌分析［M］.北京:國防工業出版社，2010.

［11］左洪福，蔡景，吳昊，等.航空維修工程學［M］.北京:科學出版社，2011.

［12］李曉陽.從航材倉儲看成本管理［J］.民航經濟與技術，2001(1):28-30.

［13］何愛云.淺談美聯航材庫存管理［J］.民航經濟與技術，2000(11):11-14.

［14］周潔敏.民用航空特色專業系統教材［M］.北京:科學出版社，2010.

［15］王曉迪. 高等學校教育裝備管理決策支持研究［EB/OL］.［2011 -12 -01］. http://cdmd. cnki. com. cn/Article/CDMD-10217-1012518514.htm.