采用馬爾科夫鏈的裝備狀態維修檢測間隔期動態決策模型研究

【后勤保障與裝備管理】

采用馬爾科夫鏈的裝備狀態維修檢測間隔期動態決策模型研究

張光明1，王勇1，范渭榮1，牛星星2

(1.武漢軍代局 駐焦作地區軍代室，河南 焦作454001； 2. 63981部隊， 武漢430312)

摘要：針對傳統狀態維修中存在的不足，分析了裝備狀態維修檢測間隔期動態決策的基本思路，研究了基于馬爾科夫鏈的裝備狀態維修檢測間隔期動態決策的關鍵技術，并在此基礎上建立了基于馬爾科夫鏈的裝備狀態維修檢測間隔期動態決策模型。

關鍵詞：狀態維修；馬爾科夫鏈；維修決策；最小交叉熵

收稿日期：2014-10-20

作者簡介：張光明(1988—)，男，碩士，助理工程師，主要從事武器系統與運用工程研究。

doi:10.11809/scbgxb2015.04.023

中圖分類號：TJ07

文章編號：1006-0707(2015)04-0081-04

本文引用格式：張光明，王勇，范渭榮，等.采用馬爾科夫鏈的裝備狀態維修檢測間隔期動態決策模型研究[J].四川兵工學報，2015(4):81-84.

Citationformat:ZHANGGuang-ming,WANGYong,FANWei-rong,etal.ResearchonStateofEquipmentMaintenanceInspectionIntervalsDynamicDecision-MakingModelUsingMarkovChain[J].JournalofSichuanOrdnance,2015(4):81-84.

ResearchonStateofEquipmentMaintenanceInspectionIntervals

DynamicDecision-MakingModelUsingMarkovChain

ZHANGGuang-ming1, WANG Yong1, FAN Wei-rong1, NIU Xing-xing2

(1.JundaishiinJiaozuoArea,WuhanJundaiju,Jiaozuo454001,China;

2.TheNo. 63981stTroopofPLA,Wuhan430312,China)

Abstract:: This paper analyzed the defects of traditional state maintenance and the state of equipment maintenance inspection interval dynamic decision-making basic train of thought. The key technology of dynamic decision-making test interval of equipment maintenance inspection based on Markov chain was discussed. Based on the above analysis, equipment state maintenance inspection interval dynamic decision-making model was established.

Keywords:statemaintenance;Markovchain;maintenancedecision;minimumcrossentropy

隨著現代武器裝備復雜性的不斷提高，其故障規律也逐漸呈現多種狀態。在現有裝備中，具有明顯耗損期情況的項目僅占很小比例。與此同時，傳統定時維修僅適用于故障率曲線具有明顯耗損期的項目，使得此種維修方式無法有效適用于現有裝備。依據RCM思想，根據不同故障規律采取不同維修方式，對于上述項目，可采用狀態維修(conditionbasedmaintenance，CBM)加以保障。

美軍給出的狀態維修的定義為：設備(武器系統)預報初始故障的主動維修的一種形式[1]。在國內狀態維修的定義為：對產品的技術狀態參數及其變化進行連續或定期的檢測，及時發現潛在故障，并預測產品的剩余壽命或功能故障將在何時發生，在功能故障發生之前或運行經濟性下降到極限時，先期制訂維修預案，有目的、有計劃地適時適度維修的一種維修方式[2]。分析上述定義可知，狀態維修是一種預防性維修，它通過定時或非定時的評估裝備狀態來判斷是否需要進行維修。在進行狀態維修時除了要決策是否需要進行維修更重要的是決策檢測間隔期。針對檢測間隔期的決策，現有的研究主要有：文獻[3]中提出了延遲時間的概念，為狀態維修建模及間隔期的確定奠定了基礎；文獻[2]中針對裝備不完全檢測過程建立了裝備等故障風險變間隔期檢測模型，然而該模型需事先了解裝備潛在故障發生時間分布；文獻[4-6]中分別采用不同方法在不同約束條件下確定了狀態維修檢測間隔期，然而此類文獻中確定的檢測間隔期均為一定值，無法適用于裝備動態狀態維修過程中；文獻[7]中對狀態維修中的評估及預測技術進行了分類，為狀態維修提供了思路。

本文主要從裝備檢測間隔期動態決策角度出發，利用類似裝備先驗信息，建立檢測間隔期動態決策模型，該模型可根據裝備實時技術狀態及時修正檢測間隔，解決缺少當前項目相關概率分布信息的檢測間隔期動態決策問題。

1傳統狀態維修決策過程分析

傳統狀態維修的基礎理論是P-F間隔期，基本方法是采取定期檢測的方式確定潛在故障發生時刻，進而采取措施避免功能故障發生。其原理如圖1所示。

圖1中：P點為潛在故障發生時刻；F點為功能故障發生時刻；二者之間時間間隔為P-F間隔期TPF。

兩次檢測時間間隔為ΔT，凈剩P-F間隔期為TC。其中，TC應大于從發現潛在故障到停機所需最大時間TS。

如圖1所示，任意時刻檢測出裝備潛在故障則進行預防性維修。該方法可有效預防裝備功能故障的發生。然而，當裝備本身可靠性較好時，過多的檢測不僅會有失經濟性而且會影響裝備性能。增長檢測間隔期或許可以減緩這一狀況，但是這又帶來一個更嚴重的問題，即可能導致某些P-F間隔期較短的裝備無法及時維修，從而導致更大的損失。

2基于馬爾科夫鏈的動態狀態維修決策建模

針對傳統狀態維修過程中存在的問題，本文將建立動態決策模型加以解決。

2.1建立馬爾科夫鏈

令：

1) 產品可靠壽命為Tr，且在壽命周期內共截取n個時間點估計其技術狀態情況；

2) 在某一狀態上存在一定的停留時間。如第i個狀態的停留時間為Δti；

3) 產品在各截取時間點的技術狀態為C1,C2,…,Cn(狀態C1為裝備啟用時對應的技術狀態；狀態Cn為可靠壽命Tr所對應的裝備技術狀態)，對應的產品可靠度為R1,R2,…,Rn；

4) 產品發生故障為狀態D，亦可當作裝備的第n+1個技術狀態。

則產品的狀態變化可由各時間節點的技術狀態之間的轉變間接表示，并且可假設各狀態之間轉變存在一定的規律。

由于產品的技術狀態是一個漸變的過程且不可逆轉，因此可假設技術狀態由較好狀態Ci轉變到較差狀態Cj的概率為Pij。當然，裝備的技術狀態也可能在下一時刻并不發生變化，如狀態Ci到Ci的概率為Pii。與此同時，裝備任意非故障狀態Ci到故障狀態D的概率為Pi(n+1)=(1-Ri)。構建馬爾科夫鏈如圖2所示。

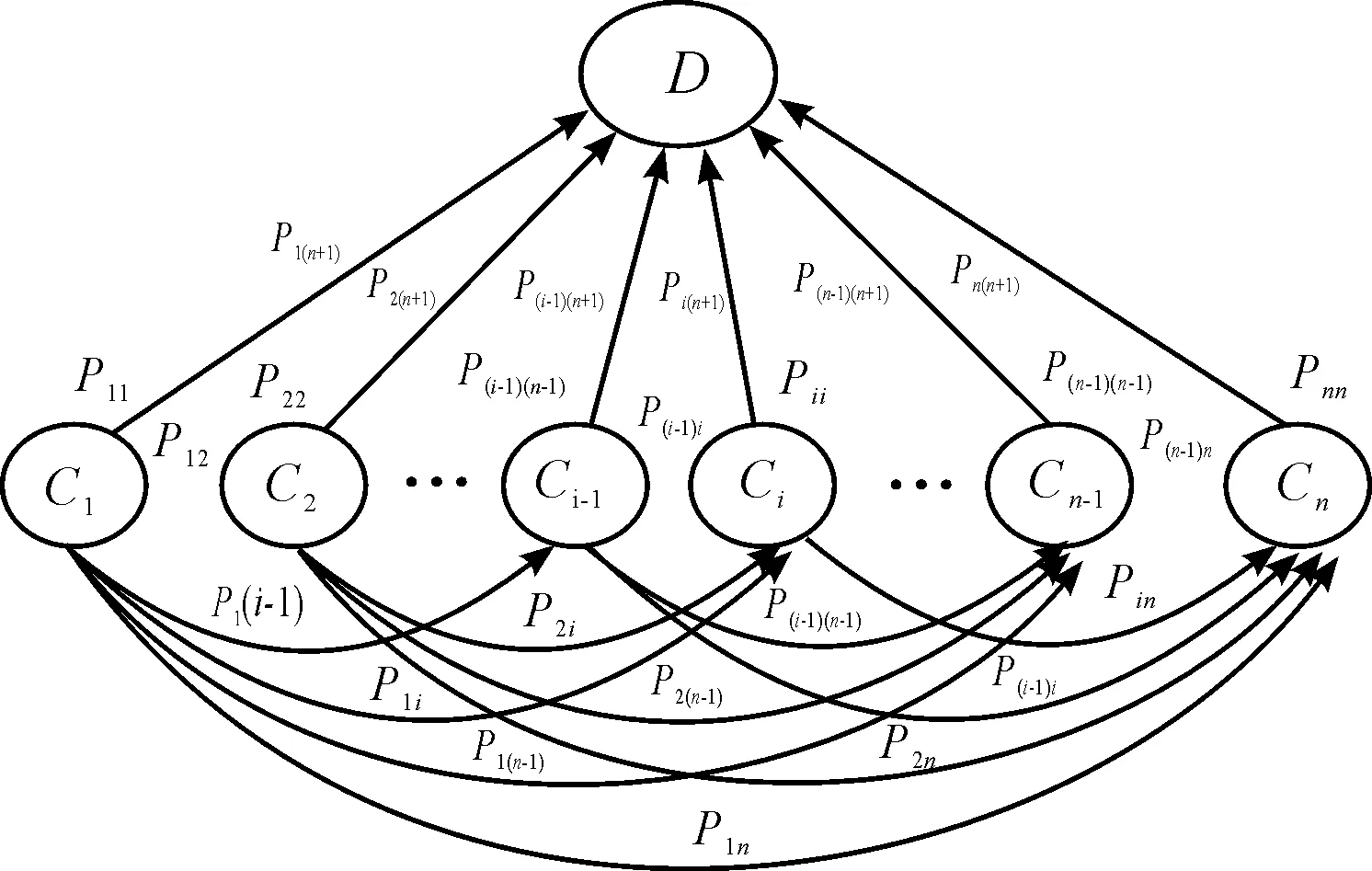
圖2　馬爾科夫鏈示意圖

2.2故障預測

假設初始狀態為Ci，時間為ti。則由該狀態到故障狀態D之間可能經歷的狀態有Ci，Ci+1，…，Cn。因為僅故障狀態D為吸收態，所以要預測故障狀態發生時刻，僅需計算故障狀態發生前所經歷的其他狀態的總停留時間即可。

設轉移矩陣為P，其(i,j)位置上的元素P(i,j)=Pij。將轉移矩陣中狀態順序重排得

其中，Q中狀態均為非常返態(非故障狀態)。

考慮訪問非故障狀態Cj的次數Yj

則

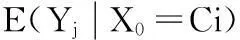
由矩陣的基本知識可知，I+Q+Q2+Q3+…=(I-Q)-1。令M=(I-Q)-1，則M在(i,j)位置上的元素Mij代表了從狀態Ci開始，訪問狀態Cj的平均次數。

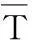
即由狀態Ci開始到達故障狀態D的最短平均步數。在各狀態停留時間已知的情況下，容易得到故障發生時間。

2.3基于馬爾科夫鏈的動態狀態維修決策模型

在進行裝備動態狀態維修時，應首先確定狀態維修的對象，然后對該對象進行狀態檢測得到信息特征量，判斷其所處狀態。繼而將該狀態與狀態集合相對比，判斷其在狀態集合中的位置，從而根據由狀態集合構建的馬爾科夫鏈進行故障預測。最后根據預測結果，決定下一步的工作。基于馬爾科夫鏈的動態狀態維修決策模型如圖3所示。

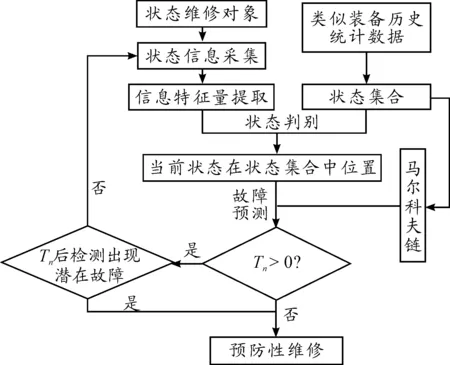
圖3　基于馬爾科夫鏈的動態狀態維修決策模型

3示例分析

對裝備建立馬爾科夫狀態時，可根據類似裝備的歷史統計信息分析結果確定馬爾科夫鏈中的狀態及其先驗轉移概率，然后利用最小交叉熵原理得出后驗轉移概率，進而確定馬爾科夫鏈。

假如，分析某裝備同類裝備歷史數據得10種裝備狀態(馬爾科夫狀態)信息如表1所示。

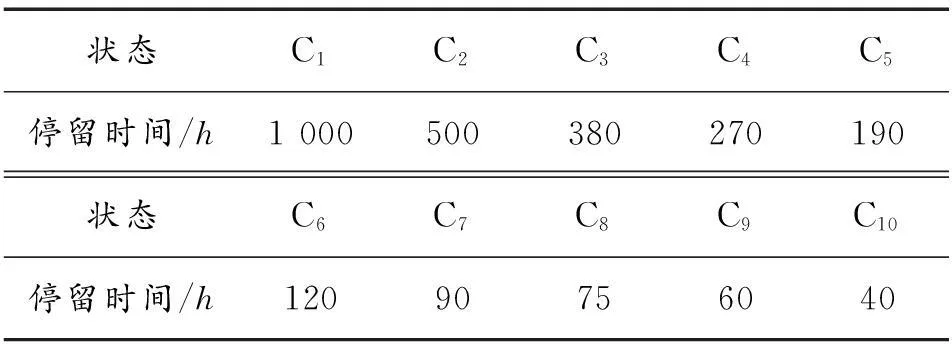
表1　10種裝備狀態(馬爾科夫狀態)信息

隨機抽樣歷史數據中某時刻處于狀態C7的裝備100臺。則以這100臺裝備為例進行分析，得90h后裝備數目與狀態對照表如表2所示。

表2　90 h后裝備數目與狀態對照

可知，初始狀態為C7時，發生一次轉移，轉移到狀態C7、C8、C9、C10、D的先驗概率分別為0.39、0.45、0.1、0.05、0.01。

為方便計算，現將狀態C7、C8、C9、C10、D分別用數值1、2、3、4、5表示。考慮所有該類裝備在歷史上2 100h時所處狀態期望值為1.9的情況下，可根據最小交叉熵原理進行如下計算

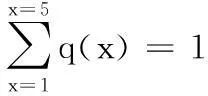
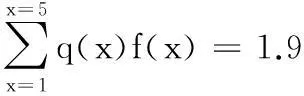
其中:p(x)為先驗概率分布; q(x)為后驗概率分布;x為狀態的數值表示形式且f(x)=x;λ0、λ1為待定系數。

經計算得初始狀態為C7時，發生一次轉移，轉移到狀態C7、C8、C9、C10、D的先驗概率分別為0.36、0.46、0.11、0.06、0.01。

依據此方法類推，即可得到轉移矩陣為

已知某裝備可靠壽命Tr=T0.8=3 000h。TS=20h，TM=30h。假設該裝備在2 000h時所處技術狀態為C7。則可建立馬爾科夫鏈如圖4所示。

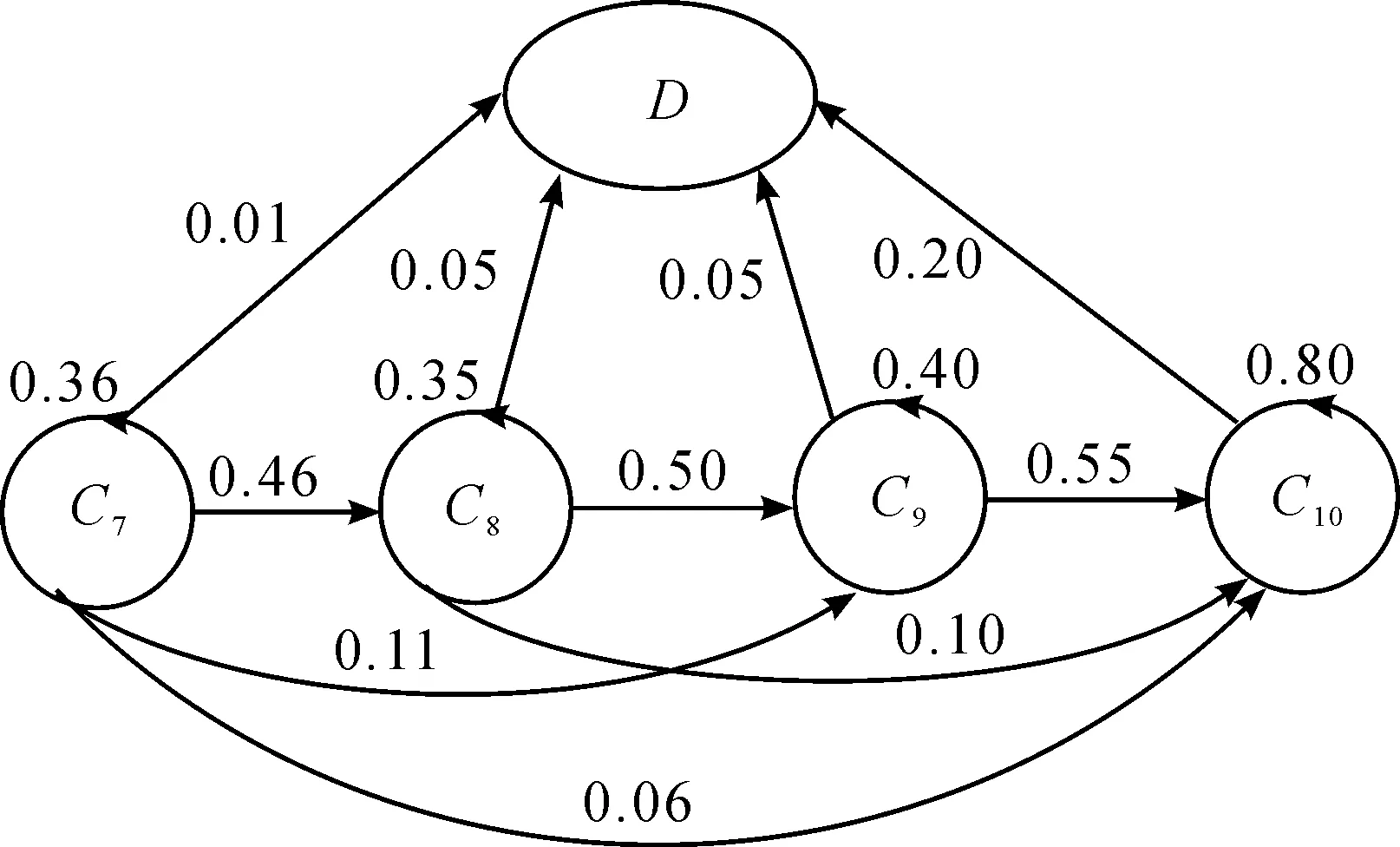
圖4　建立的馬爾科夫鏈

矩陣轉換得

計算得

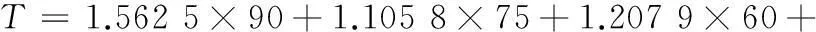
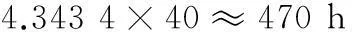
所以該裝備暫時不用進行預防性維修，在2 320 h需進行一次檢測。若再次檢測時發現潛在故障，則立刻進行預防性維修；若未發現潛在故障，則重復上述過程。

4結束語

本研究主要研究了基于馬爾科夫鏈的裝備動態狀態維修基本方法，建立了相關模型，并舉例進行了分析。文中方法可有效優化檢測間隔期，具有一定的啟發意義。在后續研究中，預測結果的精度問題值得進一步討論。

參考文獻：

[1]張偉，康建設，溫亮,等.基于信息神經網絡的狀態維修[J].儀器儀表學報，2005，26(8)：617-619.

[2]張耀輝，郭金茂，徐宗昌,等.基于估值風險的狀態維修檢測間隔期確定[J].中國機械工程，2008，19(5)：555-557.

[3]Christer A H.Innovatory Decision Making,the Role and Effectiveness of Theories of Decision in Practice [R].London:Hodder & stoughton，1973：369-377.

[4]張仕新，梅勇飛，張耀輝.基于不完善檢測的狀態維修間隔期建模[C]//裝備保障過程建模理論方法與應用學術研討會論文集.北京：兵器工業出版社，2009.

[5]陳武，張耀輝.基于多目標約束的裝備狀態維修檢測間隔期模型[C]//裝備保障過程建模理論方法與應用學術研討會論文集.北京：兵器工業出版社，2009.

[6]張仕新，劉義樂，陳杰翔.基于威布爾比例故障率模型的裝備檢測間隔期多屬性模糊決策方法[J].裝甲兵工程學院院報，2012，26(2)：20-23.

[7]孫凱，袁培賢，張耀輝,等.狀態維修中的評估預測技術研究與展望[J].質量與可靠性，2009(5)：12-15.

[8]余超， 陳夫凱，周浩. 馬爾可夫更新過程在武器裝備可靠性方面的應用[J].重慶理工大學學報：自然科學版，2014(7):137-141.

(責任編輯楊繼森)