大面積帶狀區域高程擬合方法研究

黎峻宇，劉立龍，韋相任

(1.桂林理工大學廣西礦冶與環境科學實驗中心，廣西 桂林 541004;2.桂林理工大學測繪地理信息學院，廣西 桂林 541004;3.廣西空間信息與測繪重點實驗室，廣西 桂林 541004;4.廣東省有色金屬地質局九三三隊勘測公司，廣東 肇慶 526060)

1 引 言

當前，GPS 測量技術已經在國家基礎性建設中得到廣泛應用。在這些基礎設施中，鐵路、公路、石油與燃氣管道，水渠與排灌管道，電力設施中的輸電線路，能源開發項目中的石油物探等等，往往集中在一些大面積的帶狀區域內［1］。GPS 測量直接獲得的高程是相對于WGS－84 橢球面的大地高，實際生產過程中使用的卻是相對于似大地水準面的正常高，如何直接利用GPS 大地高來獲得滿足工程需要的正常高，以便節省人力、物力和時間，一直是測量界關注和研究的一個重點，對大面積帶狀區域高程擬合方法的研究對國家基礎性建設更是具有十分重要的現實意義。然而除了文獻［1］等少數文獻涉及帶狀高程擬合研究之外，鮮有人詳細探討涉及大面積帶狀區域的高程擬合方法。高程異常轉換方法主要有四類:幾何解析法、物理大地測量法、人工智能法和混合轉換法，其中BP 神經網絡、二次曲面擬合等方法在高程擬合中得到比較廣泛的應用［2］。最小二乘支持向量機具有結構簡單、全局最優，泛化能力較好的優點，能夠很好地解決小樣本、非線性、高維數、局部極小等問題，同時還克服了神經網絡等一般學習機器中存在過學習、局部優化和樣本數量要求多的弊端，基于以上原因文獻［3］［4］等開始將其應用到高程擬合中。本文使用一個大面積帶狀的GPS 網數據為基礎，經最小二乘支持向量機、BP 神經網絡、二次曲面擬合三種方法進行高程擬合，就不同方法擬合結果進行對比分析，獲得一些具有一定價值的理論結果。最后根據這些理論結果，為國家基礎性建設中大面積帶狀區域高程擬合提出一些實用性建議。

2 擬合方法

2.1 最小二乘支持向量機

最小二乘支持向量機原理是將最小二乘引入支持向量機中，采用等式約束代替不等式約束作為損失函數。訓練過程由二次規劃問題求解轉化為線性方程組求解，同時使誤差平方項達到最小化的計算過程［3］。設給定一個有M 個訓練樣本的集合(xi，yi)，i=1，2…～M，其中訓練m 維向量，xi∈Rm，輸出數據yi∈R。按照結構風險最小化原則，函數擬合問題可轉為下列函數的約束優化問題:

約束條件為:

式中:W∈Rm為權矢量;g(xi)是將x 從輸入空間映射到特征空間的函數;ξi為誤差項;C 為正規化參數，控制對超出誤差樣本的懲罰程度，b 為偏置量。

經過簡化后得到最小二乘支持向量機函數為:

為了解決高維計算問題，引入一核函數K(xk，xj)來等效高維空間的內積形式［g(xk)g(xi)］，即:

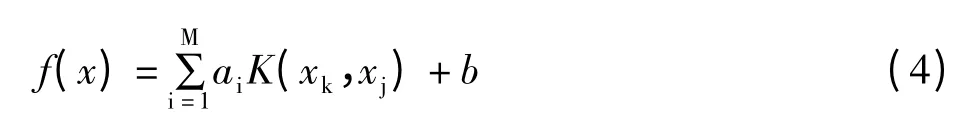
目前常用的核函數主要有多項式核函數K(x，x)=(x* y+1)p、徑向基核函數(Radial Basis Function，RBF)K(x，x)=exp［－‖x－y‖2/(2σ2)］和Sigmoid核函數k(x，xi)=tanh［v(x* xi)+c］等形式。根據數值限制條件和參數較少以及優秀的局部逼近特征，本文選擇RBF 作為支持向量機核函數。最小二乘支持向量機模型的確定最重要的是核函數參數σ 和正規化參數的選擇，廣泛采取的方法是試算法、交叉驗證法、留一法［5］。我們輸入的訓練樣本為三維向量，分別為高程點平面坐標和高程異常;輸出向量只有一維，即高程異常;基于MATLAB 工具箱中最小二乘支持向量機自帶的尋優函數進行參數尋優σ、C。

2.2 BP 神經網絡

BP 神經網絡是一個多層前向型神經網絡，其權值調整采用誤差反向傳播算法，該網絡由輸入層、隱含層和輸出層組成。設神經網絡的輸入向量為X=(X1，…，Xn)T，期望輸出為d=(d1，…，dm)T，輸入層與隱含層的權為W，其維數為n×s，閥值為θ1，維數為s×1，隱含層與輸出層的權W'，其維數為s×m，閥值為θ2，維數為m×1，其中n、s 和m 為別為輸入層、隱含層和輸出層的神經元節點數［6～7］。神經網絡的正向傳輸的計算過程如下:

隱含層的輸出計算公式為:

輸出層的輸出計算公式為:

上式中，f1(I1)、f2(I2)為隱含層與輸出層的傳遞函數，f1(I1)通常為Sigmoid 函數。f2(I2)可以為Sigmoid 函數或Purelin 函數，y2為最終的輸出值。

常用BP 神經網絡通常采用誤差反向傳播法調整連接權。神經網絡的目標函數為:

式中p 表示第p 個樣本，k 表示第k 個節點，dk表示期望輸出。

本文BP 神經網絡在MATLAB 程序環境下建立，BP 神經網絡構造各項內容如下:

(1)輸入層神經元個數3 個，分別為高程點平面坐標和高程異常;

(2)輸出層神經元個數1 個，即高程異常;

(3)訓練函數取:tansig、purelin、trainlm．

(4)設置訓練參數net．tranParam．show=100，net．tranParam．epochs=1000，net．tranParam．lr=0．01，net．tranParam．goal=1e－3，其他參數使用MATLAB 神經網絡工具箱默認的取值。

2.3 二次曲面擬合

二次曲面擬合公式為:

在(10)式中ξ 表示高程異常，(x，y)為已知點平面坐標，ε 是誤差。在式(11)中有6 個參數，此時需要重合點不少于6 個。重合點個數多于6 個，采用最小二乘原理進行數學模擬，確定模型。

將式(11)寫成矩陣形式:

對每個重合點，都可以列以上方程，在∑ε2=min的條件下，解出ai，再通過式(11)求取未知點的ξ，從而解算得各點正常高。

3 實例分析

3.1 實例數據來源

本文采用某大型工程的D 級GPS 控制網點作為樣本數據，該控制網共有點41 個，控制面積約為1 387.342 km2，控制網呈帶狀分布(點位分布如圖1所示)，水準按照二等水準測量要求施測。取33 個分布相對均勻的點作為樣本點，8 個點作為擬合點。

圖1 點位分布圖

3.2 各種方法擬合結果對比分析

為了驗證不同模型的內符合精度，就擬合求取的樣本點高程異常值與實測高程異常值之差進行統計，分析模型的可塑性。驗證內符合精度的誤差最大值(max)、誤差最小值(min)、均方根誤差(RMS)、平均絕對誤差(MAE)見表1，不同方法在對應點擬合誤差如圖2 所示。

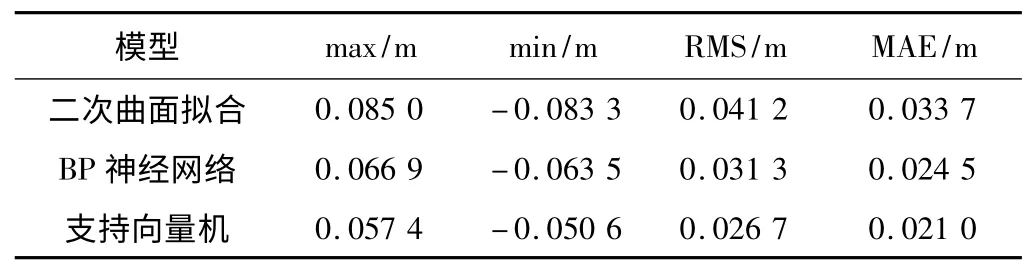
內符合精度對比 表1

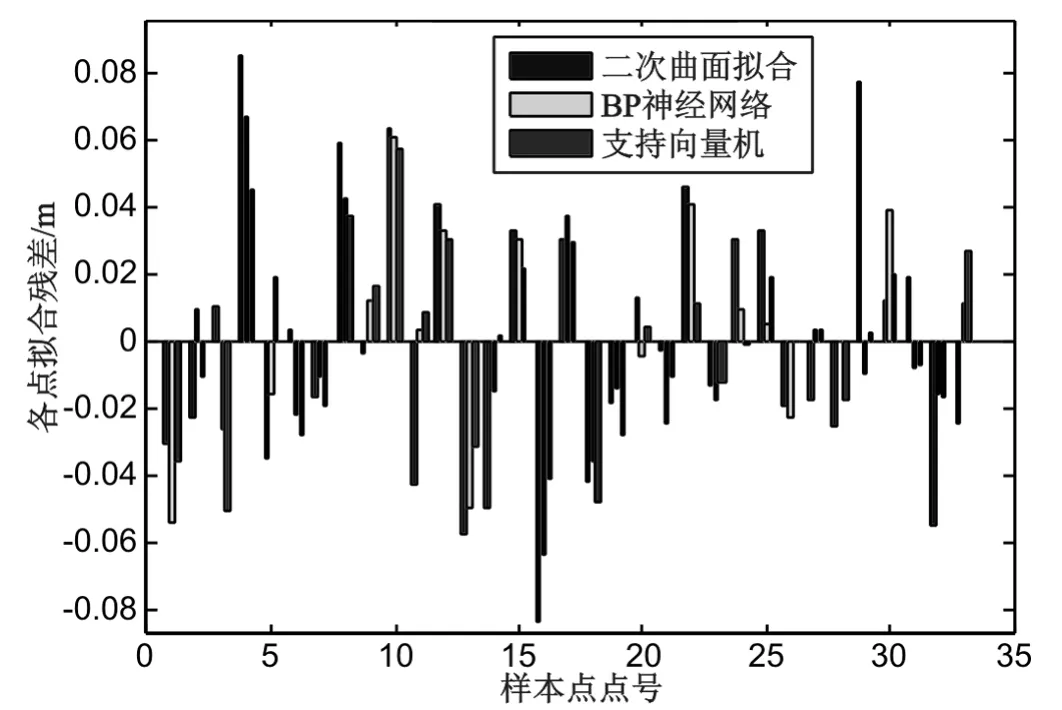
圖2 樣本點誤差分布圖

由表1、圖2 知:支持向量機的誤差最大值最小值之差在3 種方法中最小，MAE 最小，RMS 也最小;支持向量機與其他兩種方法相比，進行高程擬合可以很好地控制較大的誤差出現，同時支持向量機擬合誤差變化范圍更小，支持向量機擬合誤差更好地控制在某一范圍內;最小二乘支持向量機誤差變化最小，內符合精度最高，相對其他的擬合方法提高了約1 cm，模型具有很好的可塑性;

驗證模型的內符合精度只能達到分析模型可塑性的目的，為了充分說明各模型在大面積區域的泛化能力，還需要對模型的外符合精度進行驗證。分析了各種方法在擬合點高程異常值與實測高程異常值之差，各種方法的max、min、RMS、MAE 如表2、圖3 所示。

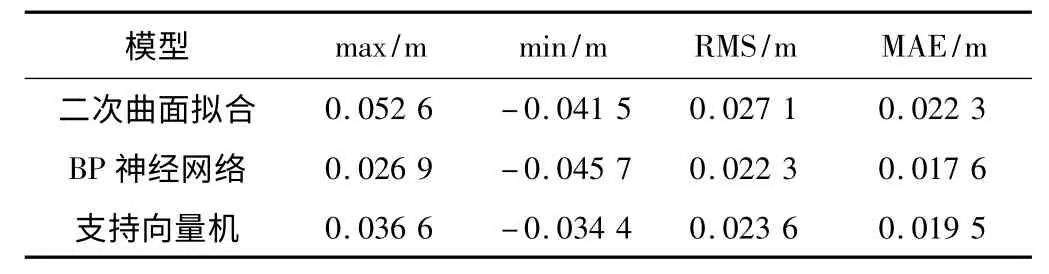
外符合精度對比 表2

圖3 擬合點誤差分布圖

通過表2、圖3 可以清晰地看到，支持向量機的誤差最大值最小值之差在3 種方法中最小;3 種方法外符合精度比較接近，支持向量機MAE 比最小的BP 神經網絡僅差1.9 mm，RMS 較最小的BP 神經網絡也僅差1.3 mm;支持向量機與其他兩種方法相比，進行高程擬合可以很好地控制較大的誤差出現，最小二乘支持向量機誤差變化較小，RMS 等于0.023 6 m，外符合精度可達cm 級精度，模型具有較好的泛化能力;

綜上，對于本文所選實例區域，最小二乘支持向量機模型的內外符合精度可以達到厘米級精度，內符合精度為0.026 7 m，外符合精度為0.023 6 m，達到高程擬合的精度要求，可應用于大面積帶狀區域高程擬合。最小二乘支持向量機擬合模型同時獲得較高的內外符合精度，具備較好的可塑性和泛化能力。

4 結 論

本文以大面積帶狀區域GPS 控制網為實驗區域，使用最小二乘支持向量機、BP 神經網絡、二次曲面擬合三種方法實施高程擬合，進行大面積帶狀區域高程擬合方法研究。通過探討得出:

(1)最小二乘支持向量機可應用于大面積帶狀區域高程擬合，在本文大面積帶狀區域中擬合精度達到較理想的厘米級，且三種擬合方法的泛化能力很接近，BP 神經網絡最強，最小二乘支持向量機次之。

(2)最小二乘支持向量機在大面積帶狀區域高程擬合中具有相當的優勢，可同時獲得較高的內外符合精度，該方法在可塑性優勢明顯的同時也具有較強的泛化能力。

(3)同一區域，不同方法擬合精度不同，本文試驗獲取數據具有局域性，不同的高程擬合方法在其他區域的適用性有待進一步驗證。

綜上所述，在大面積區域，進行高程擬合，建議可采用最小二乘支持向量機模型。

［1］高西峰．GPS 水準在帶狀區域似大地水準面精化中的應用研究［D］．長安，長安大學，2007．

［2］任超，吳偉，黃征凱等人．基于ACI 準則的徑向基函數網絡在GPS 高程轉換中的應用［J］．測繪科學，2013(2):77～79．

［3］黃磊，張書畢，王亮亮等人．粒子群最小二乘支持向量機在GPS 高程擬合中的應用［J］．測繪科學，2010(5):190～192．

［4］姬張建，袁運斌，盛傳貞．混沌粒子群支持向量機并考慮地形改正的GPS 高程擬合［J］．大地測量與地球動力學，2010(2):95～98．

［5］吳吉賢，杜海燕，張耀文．LSSVM 回歸模型在局部區域GPS 高程擬合中的應用［J］．測繪科學，2013(6):66～68．

［6］張德豐．MATLAB 神經網絡應用設計［M］．北京:機械工業出版社，2011:137～139．

［7］王小輝，王琪潔，丁元蘭等人．基于二次曲面和BP 神經網絡組合模型的GPS 高程異常擬合［J］．大地測量與地球動力學，2012(6):103～106．

［8］張昊，王琪潔，朱建軍等人．樣本數據預處理對基于BP神經網絡的高程轉換的影響［J］．大地測量與地球動力學，2011(2):125～128．

［9］邱衛寧．具有穩健初值的選權迭代法［J］．武漢大學學報·信息科學版，2003(4):452～454．

［10］張恒璟，程鵬飛．基于GPS 高程時間序列粗差的抗差探測與插補研究［J］．大地測量與地球動力學，2011(4):71～75．