不動產測量中的環玦狀房地產面積計算方法
徐興彬
(1.廣東工貿職業技術學院 測繪系,廣東 廣州 510510)
廣州某住宅區開發建設持續10余a,其中有一片別墅區規劃建設成數條環玦狀地帶(圖1),測量時發現同一條環玦帶的同一條弧線上各地塊的圓弧長相等,但面積卻不一定相等。規劃時設計人員只將各段圓弧平均分配再依次相連成各個單位地塊,而且認定各單位地塊的面積均等。在管理廣州市寸土寸金的別墅用地時,要體現不動產測量登記工作的科學性與嚴肅性,就必須計算出每一塊地的面積準確值[1,2]。
圖1所示為別墅住宅區某一部分的實地情況,規劃設計人員先在地形圖上確定數條沿直徑方向的放射狀縱向主干道(例如,其中2條主干道中線為ABEO與CDFO)。將中線分別往兩邊平移獲得道路寬度(中線退縮后分別為2am和2bm),與縱向主干道垂直的各條道路的中線或邊線均為同心圓弧,各圓弧均有確定的半徑。將各段路邊線圓弧等弧長劃分并依次相連,便得到各個環玦狀小地塊(宗地范圍),各小地塊的測量放線同樣先計算出各平均小段圓弧的弦長,然后用鋼尺按距離放線。現在要求計算環玦中各小地塊的面積準確值。先利用初等幾何計算出圖中玦形A0B0C0D0所包含的面積(即圖2中的A0B0BnAn),整理得到:
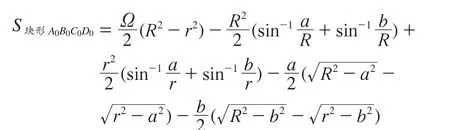
此時,如果假定圖2中各小地塊具有相同的面積,則可以將上述面積S玦形A0B0C0D0除以A0B0C0D0中地塊的個數n,即得各小地塊的面積。根據下面的推導分析,可證明此假設是錯誤的。
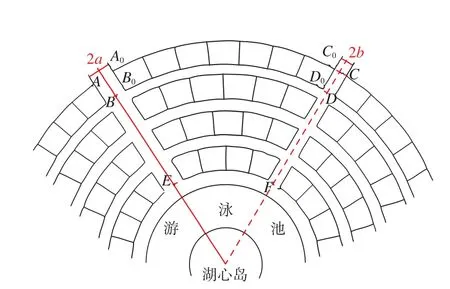
圖1 小區別墅平面圖

圖2 面積推算示意圖
1 公式推導
圖2中,2條縱向道路的路中線AB、CD之間的夾角為Ω,路寬分別為2a和2b,該地段總地塊數為n,各地塊前后圓弧半徑分別為r、R。建立如圖中的獨立直角坐標系oxy,針對圖中第i個地塊,則有:

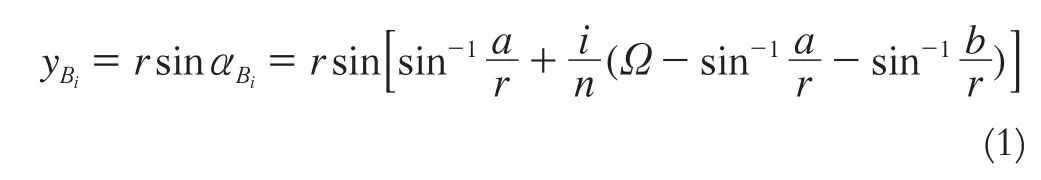
因此,直線Ai Bi和Ai-1Bi-1的方程式為:
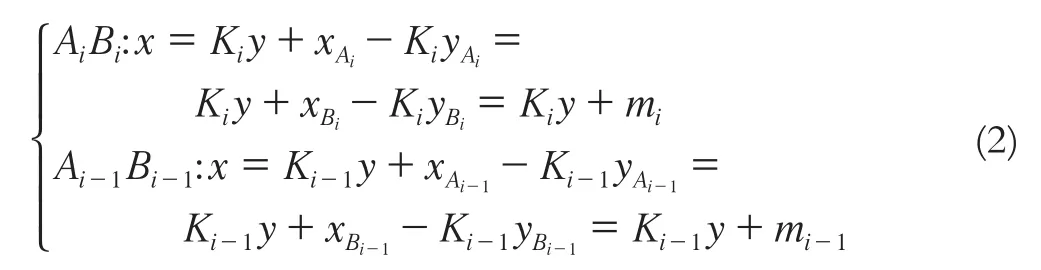
其 中,Ki =(xAi-xBi)/(yAi-yBi);Ki-1=(xAi-1-xBi-1)/(yAi-1-yBi-1)。
根據二重積分的幾何原理,則該塊面積為[3]:
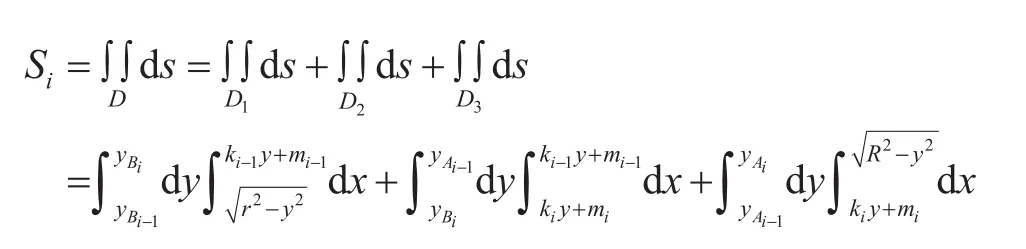
積分后將式(1)、(2)代入,整理得:
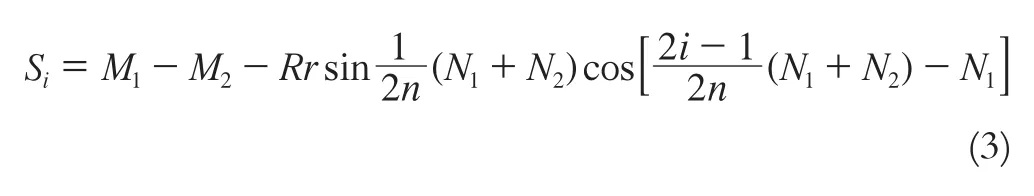
它們均為常量,其幾何意義為:M1為大圓弧Ai-1Ai所圍成扇形OAi-1Ai的面積;M2為小圓弧Bi-1Bi所圍成扇形OBi-1Bi的面積;N1、N2則均為一夾角(見圖2)。根據式(3),當i發生變化時,各小塊的面積Si依據它的位置變化而有所不同。
2 分析討論
2.1 關于函數Si=f(i)的極值
對于式(3),因為Si=f(i)為連續函數,對i求微分并令其等于0:
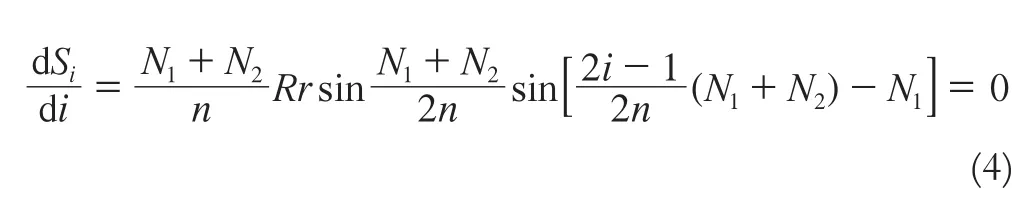
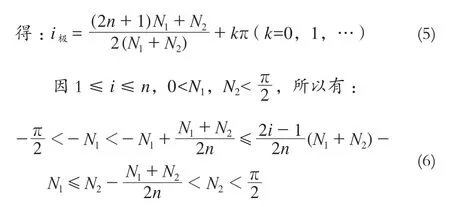
則式(5)中k≡0,即Si=f(i),當1≤i≤n時只有
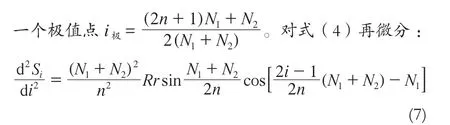
根據式(6),有 d2Si /di2>0,即函數Si=f(i)在i屬于[1,n]時具有向上凹的連續曲線,且在處有極小值:
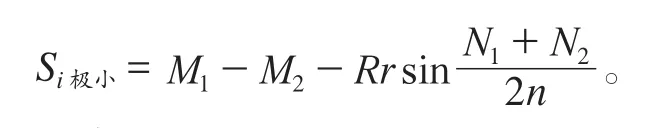
2.2 函數Si = f(i)的圖形
令1≤i≤j≤n,根據式(3)有:
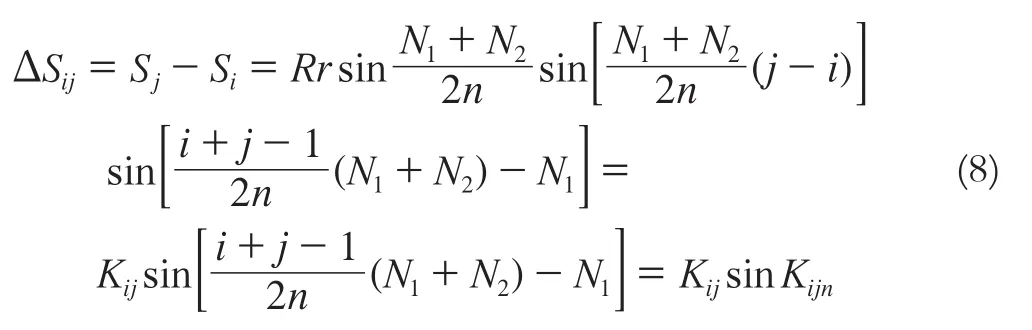
令i=1,j=n,則
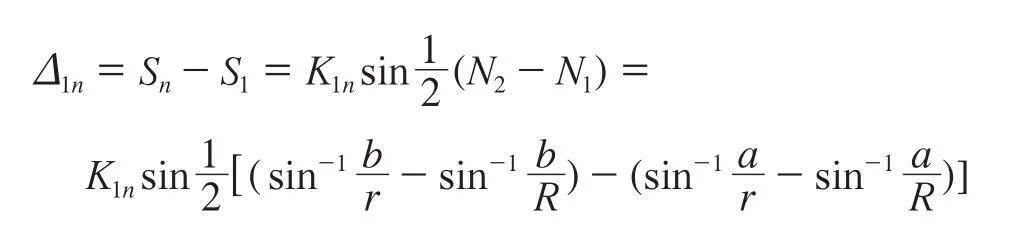
令j=n代入式(8),再令

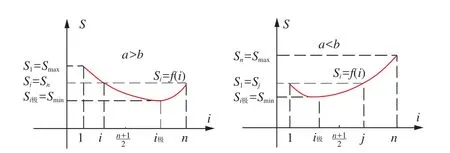
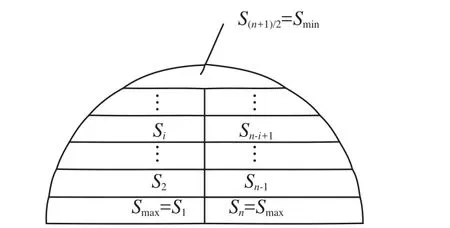
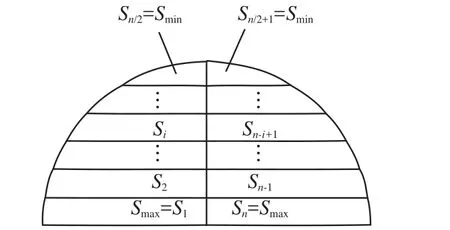
圖3 a>b時Si=f(i)的圖形 圖4 a 最后再考慮圖2中最大塊與最小塊的面積差值。 參照圖3,將i=1、j=i極代入式(8)得: 同樣,參照圖4,將i=i極,j=n代入式(8),得: a=b,即N1=N2=N,代入式(3)得: 將N1=N2=N代入式(5)得: 將N1=N2=N代入式(8),得: 式(14)的幾何意義見圖5、圖6,它們可以比較形象直觀地反映出各個小地塊面積的大小及其相互關系:當a=b時,靠路邊的2塊地面積最大且相等,然后逐漸向中部縮小(且Si=Sn-i+1=Sj),最后收斂于最中部的地塊。如果n為奇數,則收斂于第(n+1)/2塊(圖5);如果n為偶數,則收斂于第n/2塊和n/2+1塊(Sn/2=Sn/2+1),如圖6。 圖5 n為奇數時地塊面積的變化趨勢 圖6 n為偶數時地塊面積的變化趨勢 將N1=N2=N代入式(9)或式(10),則可得到當a=b時,最大塊與最小塊的面積差值: 當a=b時, 設i=n=1并 代入式(3), 則 圖2中A0B0BnAn的面積為: 此式與本文開頭推導結果完全相同。 當a=b=0,i=n=1, 代入式(3), 則(圖2),此即為標準圓玦面積。 綜上所述,可以得出如下結論: 1)將一段環玦按等弧長均勻劃分后(見圖2,要求a、b不能同時為0),各個小環玦狀地塊面積并不一定相等,它們具有面積最大值和最小值(同時也是極小值)。最大值總是靠近縱向路較寬的一邊(路邊第一塊為最大),最小值地塊則靠近中央部位附近偏向路較窄的一邊(a、b相差越小時越接近中央)。 2)當a=b時,靠近2條縱向路邊的2小塊面積最大且相等,最小者為最中央的一塊(n為奇數塊時)或2塊(n為偶數塊時),其余小塊由縱向路邊向中央位置方向推算時,對應相等并逐漸縮小。 3)式(3)適用于各種圓曲線(小區道路一般無需設緩和曲線)道路的路邊建筑物地塊的面積計算。如將圓曲線設計為緩和曲線,則只需將圓曲線方程替換為緩和曲線方程,之后按同樣方法計算推導即可。 [1]GB/T17986-2000.房產測量規范[S]. [2]CJJ/T 8-2011.城市測量規范[S]. [3]同濟大學數學系.高等數學[M].北京:高等教育出版社,2007 [4]藍悅明,康雄華.不動產測量與管理[M].武漢:武漢大學出版社,2008 [5]徐興彬,邱錫寅,黃維章,等.基礎測繪學[M].廣州:中山大學出版社,2014 [6]王勝兵,戴明強,黃登斌.基于雙線性插值擬合的山形曲面面積計算[J].兵工自動化,2012,31(3):42-43 [7]王小昆,馮仲科,聶玉藻.應用三次樣條法進行林地面積量算的研究[J].測繪科學,2004,29(4):57-60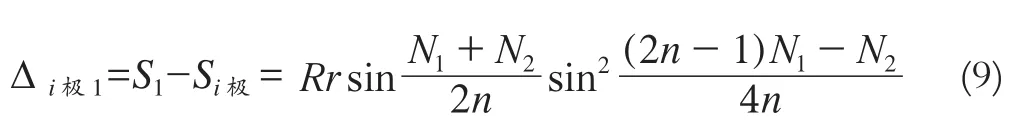
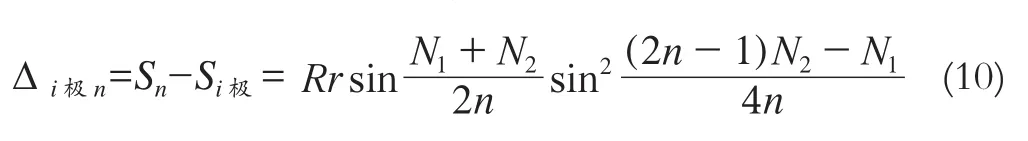
2.3 分析a=b的情況
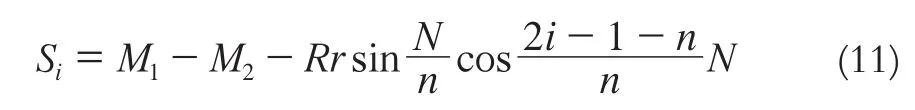


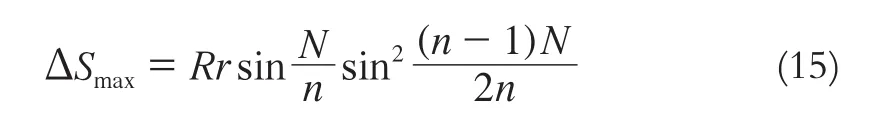
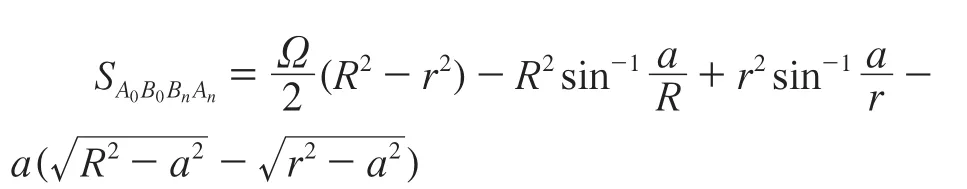
3 結 語

