基于仿生學(xué)的高速列車減阻機(jī)理數(shù)值模擬＊

王志強(qiáng)

（中國民航大學(xué)財(cái)務(wù)處，300300，天津∥講師）

很多大型海洋生物快速游動(dòng)時(shí)，其理論做功消耗是實(shí)際攝食能量的7倍以上。這是著名的雷格悖論。深入研究表明，這些大型的海洋生物體表覆蓋著一層微小尺度的溝槽，在其快速游動(dòng)時(shí)，這些溝槽能有效減小水阻，從而降低海洋生物對能量的依賴度，獲得極高的速度。這一發(fā)現(xiàn)引發(fā)人們對海洋生物減阻仿生學(xué)的研究［1－2］。其中鯊魚皮表面呈現(xiàn)出良好的剛性結(jié)構(gòu)并具有規(guī)律的排列特性，便于仿制設(shè)計(jì)與生產(chǎn)加工，逐漸成為減阻仿生學(xué)研究的主要對象［3］。

本文將鯊魚皮表面溝槽結(jié)構(gòu)應(yīng)用到高速列車減阻領(lǐng)域中，采用格子Boltzmann方法（LBM）［4］研究微小尺度溝槽表面流動(dòng)特性。LBM是近幾十年來發(fā)展迅速的一種計(jì)算流體力學(xué)新方法，本質(zhì)上是一種介于宏觀與微觀之間的模擬方法。其使用運(yùn)動(dòng)分子的分布函數(shù)來代替格子中的運(yùn)動(dòng)分子，既保留了微觀層次的自動(dòng)演化特性，又兼有宏觀層次的方程易于數(shù)值求解的優(yōu)勢。本文采用LBM中最常用的Bhatnagar－Gross－Krook（BGK）［5］模型模擬水在盾鱗形溝槽表面的流動(dòng)特性，獲得了溝槽表面內(nèi)流線變化規(guī)律；分析溝槽減阻機(jī)理，計(jì)算阻力損失系數(shù)，得到不同雷諾數(shù)下的溝槽表面減阻能力。

1 數(shù)學(xué)模型

本文采用文獻(xiàn)［6］提出的二維九速（D2Q9）正方形格子模型。格子的時(shí)空演化方程為：

式中：

fi（x，t）——質(zhì)點(diǎn)在x處t時(shí)刻沿著ei方向的粒子分布函數(shù)；

c——粒子遷移速度，c＝δx／δt（δx為格子長度，δt為時(shí)間步長）；

fi，（eq）（x，t）——局部平衡態(tài)分布函數(shù)；

τ——單松弛時(shí)間，用來控制fi（x，t）趨近于fi，（eq）（x，t）的速率；

ei——離散速度矢量。

D2Q9模型示意圖如圖1所示，每個(gè)格點(diǎn)的速度離散成9個(gè)方向。即：

圖1 D2Q9模型示意圖

fi，（eq）（x，t）遵 循 Maxwell平衡態(tài)分布函數(shù)，即：

式中：

wi——權(quán)系數(shù)，i＝0時(shí)，wi＝4／9；i＝1，2，3，4時(shí)，wi＝1／9；i＝5，6，7，8時(shí)，wi＝1／36；

ρ——密度；

ueq——粒子平衡狀態(tài)速度。

流體的宏觀密度、速度和壓力可以表示為分布函數(shù)的統(tǒng)計(jì)平均，即：

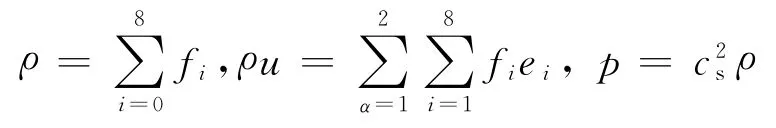
式中：

cs——等溫音速

使用LBM模擬時(shí)，參數(shù)的設(shè)置應(yīng)遵循LBM方法與實(shí)際流場的相似關(guān)系。即需要保證它們的Euler、Reynolds、Strouhal和Froude數(shù)相等。

式中：

λl，λu，λp，λρ，λv，λt——分別為長度相似比、速度相似比、壓力相似比、密度相似比、運(yùn)動(dòng)粘度相似比、時(shí)間相似比。

假定實(shí)際流場的參數(shù)分別為特征長度L、特征速度u0、波速C、時(shí)間t、壓力P、密度ρ，、運(yùn)動(dòng)粘度v，LBM方法模擬該流場時(shí)取特征長度為l，則有：其它參數(shù)可按相似率確定。于是得到LBM的參數(shù)如下：

對應(yīng)的τ根據(jù)運(yùn)動(dòng)粘性系數(shù)來確定：

2 數(shù)值模擬

本文模擬流體流經(jīng)二維通道的流動(dòng)特性。流通通道長40 mm，高8 mm，上表面為光滑壁面，下表面均勻布置微小尺度的仿鯊魚皮表面的溝槽。研究表明，鯊魚皮表面呈盾鱗形狀（見圖2），盾鱗長度為1 mm左右。根據(jù)鯊魚皮表面形狀特點(diǎn)，將其簡化為便于生產(chǎn)加工的形狀，如圖3a）所示。圖中，s＝2 mm，h＝1 mm，s1＝1 mm。則流通通道如圖3b）所示。選用干空氣（20℃）為流動(dòng)介質(zhì)。干空氣密度為1.25 kg／m3，粘度為15.06 m2／s。

編寫LBM代碼進(jìn)行模擬計(jì)算。網(wǎng)格劃分采用800×100個(gè)格子，邊界條件設(shè)置如下：

（1）上壁面和下壁面溝槽表面均設(shè)置為反彈邊界。直邊固體邊界使用標(biāo)準(zhǔn)反彈格式，復(fù)雜的曲邊固體邊界則使用具有二階精度的BFL格式［7］。該格式按照反彈方向?qū)Ψ植己瘮?shù)做碰撞后插值。

式中：

δf′——相應(yīng)的壁面運(yùn)動(dòng)速度引起的校正，取壁面速度為0。

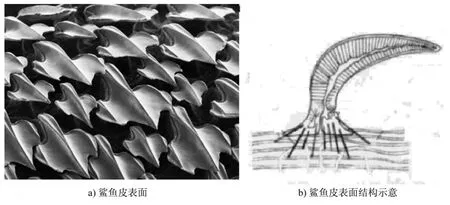
圖2 鯊魚皮盾鱗形溝槽表面

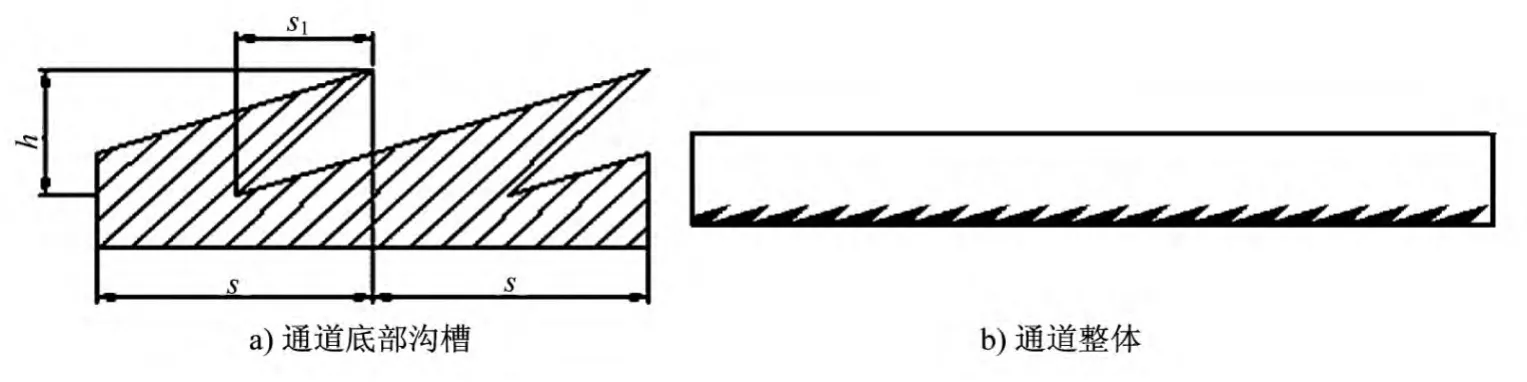
圖3 通道結(jié)構(gòu)示意圖

（2）左邊界設(shè)置為速度入口邊界，右邊界設(shè)置為自由出流邊界：當(dāng)x＝0時(shí)，u＝f（uin），v＝0；當(dāng)其中速度邊界采用非平衡外推方式［6］，即：

3 模擬結(jié)果

本文模擬不同的雷諾數(shù)下盾鱗形溝槽內(nèi)表面通道流動(dòng)特性，并根據(jù)模擬結(jié)果計(jì)算不同雷諾數(shù)下的阻力損失系數(shù)。計(jì)算公式如下：

式中：

D——流通通道當(dāng)量直徑；

ua——流動(dòng)穩(wěn)定狀態(tài)下流體的平均流速；

Δp——通道入口與出口的壓力差。

為了更好地分析盾鱗形溝槽的減阻能力，模擬了水在光滑通道內(nèi)的流動(dòng)特性。定義η為減阻系數(shù)，其計(jì)算式為：

式中：

Δpsmooth——水流經(jīng)光滑通道的壓力損失；

Δpgrooved——水流經(jīng)溝槽通道的壓力損失。

模擬雷諾數(shù)Re分別為20、50、100、150和200時(shí)水的流動(dòng)，并計(jì)算不同雷諾數(shù)時(shí)的阻力損失系數(shù)和減阻系數(shù)。計(jì)算結(jié)果如表1所示。

表1 盾鱗形溝槽表面阻力損失系數(shù)與減阻能力模擬結(jié)果

由表1可知，隨著雷諾數(shù)的增大，溝槽表面的減阻能力也隨之增強(qiáng)。

圖4所示盾鱗形溝槽表面流道內(nèi)的流場圖可進(jìn)一步分析盾鱗形溝槽表面的減阻機(jī)理。由圖中流線分布可以看出，溝槽結(jié)構(gòu)的存在改變了表面近壁區(qū)的流場特性，在溝槽中形成穩(wěn)定的低速漩渦，且漩渦的大小、形狀和位置基本相同，渦的上部與來流方向相同，渦的下部與來流方向相反。這些渦穩(wěn)定在波谷，沒有向周圍擴(kuò)散，互相之間無影響，形成了低速流動(dòng)的“第二渦群”，使得自由來流不與通道表面接觸，而是在平行人工渦上流動(dòng)，起到了類似“滾動(dòng)軸承”的作用，從而減小流體與固體壁面的接觸。即溝槽減小了流體流動(dòng)過程中與固體壁之間的摩擦阻力，起到了減阻的作用。

4 結(jié)構(gòu)優(yōu)化設(shè)計(jì)

對盾鱗形表面結(jié)構(gòu)進(jìn)行優(yōu)化設(shè)計(jì)。改變盾鱗形溝槽s與h的取值，進(jìn)行變參數(shù)模擬。模擬結(jié)果如表2所示。

圖4 盾鱗形溝槽表面流場局部放大圖

表2 不同盾鱗形溝槽表面結(jié)構(gòu)參數(shù)對減阻系數(shù)的影響

由表2可看到，當(dāng)h固定不變（h＝1 mm）時(shí)，隨著s1的增加，溝槽的減阻系數(shù)η先增加后減弱，但總體變化不大；當(dāng)s1固定不變（s1＝1 mm）時(shí)，h的變化對溝槽減阻系數(shù)η的影響較大，隨著h的增加，η也隨之增加，當(dāng)h＞1 mm時(shí)，增加程度明顯減弱。改變s1和h，使得溝槽內(nèi)部體積變化，從而影響了溝槽內(nèi)部旋渦的形成。獲得最佳的二次旋渦可有效減小流動(dòng)過程中的阻力損失。

5 結(jié)語

盾鱗形溝槽結(jié)構(gòu)的減阻仿生研究是一門交叉的學(xué)科，本文采用LBM模擬方法研究了盾鱗形溝槽表面的減阻機(jī)理與不同雷諾數(shù)下的減阻能力。盾鱗形結(jié)構(gòu)的優(yōu)化設(shè)計(jì)有待進(jìn)一步的研究。我國是能耗大國，節(jié)能減排刻不容緩，迫切需要開發(fā)節(jié)能降耗的創(chuàng)新技術(shù)，因此，積極開展仿生溝槽表面的開發(fā)與應(yīng)用具有重要意義。

［1］Wahidi R，Chakroun W，Al－Fahed S.The behavior of the skin friction coefficient of a turbulent boundary layer flow over a flat plate with differently configured transverse square grooves［J］.Experimental Thermal and Fluid Science，2005，30（2）：141.

［2］Wainwright S A，Vosburgh F，Hebrank J H.Shark skin：function in locomotion［J］.Science（New York，NY），1978，202（4369）：747.

［3］Russo R A.Notes on the external parasites of California in shore sharks［J］.California Fish and Game，1975，61：228.

［4］He Xiaoyi，Luo Lishi.Theory of the lattice Boltzmann method：from the Boltzmann equation to the lattice Boltzmann equation［J］.Physical Review E，1997，56（6）：6811.

［5］Chen Shiyi，Doolen G D.Lattice Boltzmann method for fluid flows［J］.Annual Review of Fluid Mechanics，2003，30（1）：329.

［6］Bhatnagar P L，Gross E P，Krook M.A model for collision processes in gases，I.Small amplitude processes in charged and neutral one component systems［J］.Physical Review，1954，94（3）：511.

［7］Qian Yuehong，d＇Humieres D，Lallemand P.Lattice BGK models for Navier Stokes equation［J］.EPL（Europhysics Letters），1992，17（6）：479.