基于跟馳數據采集分析的各異性跟馳模型

敬 明，王 昊，王文靜

(1.交通運輸部公路科學研究院，國家智能交通系統工程技術研究中心，北京100088;2.交通運輸部公路科學研究院，智能交通技術交通行業重點實驗室，北京100088;3.東南大學 交通學院，南京210096)

0 引 言

交通流中車輛和駕駛員的個體差異導致跟馳行為中車輛的軌跡不一致，反映到交通流跟馳模型中，表現為不同車輛的參數標定結果出現差異。依據車輛跟馳數據對跟馳模型參數進行標定和分析是將交通調查數據與車輛和駕駛員特性聯系起來的方法之一。Newell 于2002 年提出一個簡化的跟馳模型，模型中只包含兩個參數，但是可以提供足夠的仿真精確度［1-2］。該模型的提出隱含了一個觀點，即通過兩組相互獨立的變量就可以描述車輛和駕駛員在跟馳行為中的特性。文獻［3-4］對調查采集的跟馳數據直接進行因子分析，并用4 個因子來描述車輛和駕駛員的特性，其中前3 個因子提供的信息量約占據信息總量的95%。許多經典跟馳模型方程中含有數量較多的參數，例如智能駕駛模型(Intelligent driver model，IDM)方程中有7 個參數。如果只需要4 個或更少的因子就可以描述車輛和駕駛員特性，則模型的參數間可能存在一定的相關關系，通過分析模型參數在不同個體間的變化規律，可以將參數歸納為數量更少的因子，從而簡化描述車輛和駕駛員的個體特征。文獻［5-8］對各異性跟馳模型進行了研究，但是在描述個體特征時，沒有考慮到模型參數間的相關性，參數都以相互獨立的方式離散，并且也沒有進行跟馳數據的采集分析工作。

本文在上述研究的基礎上，提出了一種基于跟馳數據研究車輛和駕駛員特性分布的方法，以優化速度模型(Optimal velocity，OV)［9］和IDM 模型［10］為例，基于模型參數的相關性提出了特征因子的概念，根據跟馳模型參數取值研究了特征因子(即車輛和駕駛員特性)的分布情況。在已知特征因子分布時，通過特征因子與模型參數的換算建立了各異性IDM 模型，實現了對異質交通流的仿真分析。

1 車輛跟馳數據的采集和處理

1.1 跟馳數據采集

在江蘇省南京市，于天氣晴朗的工作日下午14∶ 00 ～17∶ 00，沿龍蟠中路-瑞金路-御道街-中山東路-龍蟠中路的路線，采用跟車調查的方法，使用車載激光測速測距一體化系統采集了25 位駕駛員(包括16 位專業駕駛員和9 位業余駕駛員)所駕駛車輛在沿全程路線行駛過程中的速度和車輛間距信息。數據采集系統包括:車載激光測距儀一臺，GPS 一個，處理機一臺。其中GPS用來測量試驗車速度;車載激光測距儀用來測量試驗車與前車的間距。對于每個駕駛員，采集的原始數據以矩陣形式存儲，矩陣的第1 列為時間(時間步長為0.1 s);第2 列為本車的速度;第3列為本車與前方車輛的間距。

1.2 數據篩選和平滑處理

車輛和駕駛員在加速、減速的行駛過程中會體現出不同的跟馳特性，因此篩選出對應不同行駛狀態的跟馳數據，并在此基礎上分別進行參數標定。

設采集到的第i 個駕駛員的數據矩陣Di共有a 行3 列，根據時間、速度和車輛間距初步將數據分段:對于數據組中任意一行k(0 ＜k ≤a－1)，如果Di(k+1，1)－Di(k，1)≥1，即時間突變超過1 s，說明采集計時出現間斷;如果Di(k+1，2)－Di(k，2)≥1，即速度突變超過1 m/s，說明采集計時可能出現間斷;如果Di(k+1，3)－Di(k，3)≥3，即間距突變超過3 m，說明前方車輛換道或者采集計時出現間斷，則在k 行后添加分隔符將數據分開。

將Di中時間持續時長≥10 s 的數據段進行保留，將其他數據刪除，從25 個駕駛員的數據中得到509 個數據段。數據篩選條件針對跟隨同一輛前車的車輛行駛過程，得到的數據組可以描述車輛的跟馳狀態，記為

對Di中的速度數據進行差分計算出車輛加速度，從加速度為正值時開始記錄時間長度，如果加速度出現0 或負值并且持續時間超過1 s，則終止記錄，記錄的時長t=te－ts－tm，te為結束記錄的時間;ts為開始記錄的時間;tm為終止條件中加速度為負數或0 狀態持續的時間。如果記錄時長≥6 s，則對該數據段進行保留，將不符合條件的數據刪除，從25 個駕駛員的數據中得到137 個數據段。數據篩選條件針對跟隨同一輛前車的車輛行駛過程中本車加速度大于0 的情況，得到的數據組可以描述車輛的加速狀態，記為

對Di中的速度數據進行差分計算出車輛加速度，從加速度為負值時開始記錄時間長度，如果加速度出現0 或正值并且持續時間超過1 s，則終止記錄，記錄的時長t=te－ts－tn，tn為記錄終止條件中加速度為正數或0 狀態持續的時間。如果記錄時長≥6 s，則對該數據段進行保留，將不符合條件的數據刪除，從25 個駕駛員的數據中得到285 個數據段。數據篩選條件針對跟隨同一輛前車的車輛行駛過程中本車加速度小于0 的情況，得到的數據組可以描述車輛跟馳過程中的減速狀態，記為

1.3 跟馳模型參數標定

式中:k 為靈敏度參數;v(xn－1(t)－xn(t))為由車輛間距決定的優化速度，本文采用Helbing 與Tilch 提出的優化速度方程［12-13］為:

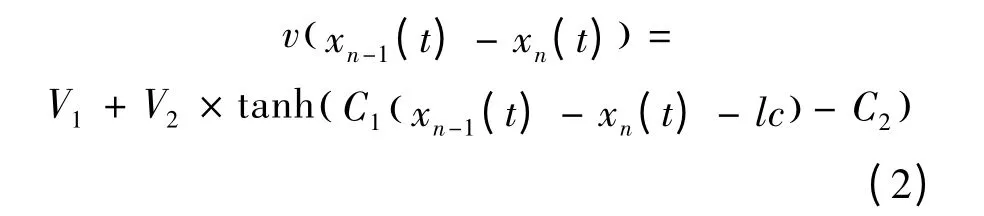
式中:lc 為車身長度，V1、V2、C1、C2為相關參數。

IDM 模型的表達式為:

式中:Δv(t)為本車與前車的速度差;s*(vn(t)，Δv(t))為當前狀態下駕駛員的期望間距;w 為起步加速度;d 為舒適減速度;δ 為加速度指數;v0為車輛的理想速度;s0為靜止安全距離參數;s1為與速度相關的安全距離參數;T 為駕駛員在剎車時需要的反應時間。

對于式(4)，當兩車速度差為較大負值時，會產生負的期望間距，而在式(3)中負的期望間距會被當做正值來處理，產生錯誤，因此本文通過式(5)對期望間距進行修正。

參數的標定過程采用最小二乘法，算法的目標是使下述目標函數取最小值:

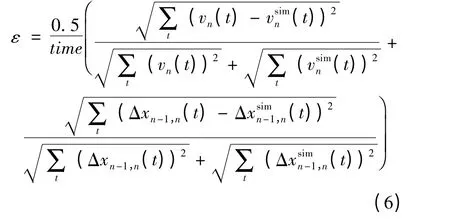
式中:time 為數據段包含的時間長度;vn(t)、分別為t 時刻實測速度和根據擬合參數計算的速度;分別為t 時刻實測車輛間距和根據擬合參數計算的車輛間距。

為了達到較好的標定效果，目標函數中綜合考慮了車速和車輛軌跡的擬合。由于加入time－1項，計算的殘差是時間段內速度和位移的擬合差值在每個時間步內的平均值，這樣便于進行時間長度不同的數據段之間的比較。

根據數據組的數據分別對OV 模型和IDM 模型進行參數標定。如果對于駕駛員n，在加速過程篩選出k 個數據段，得出了k 組參數標定結果，則該駕駛員對應加速過程的參數標定結果為:

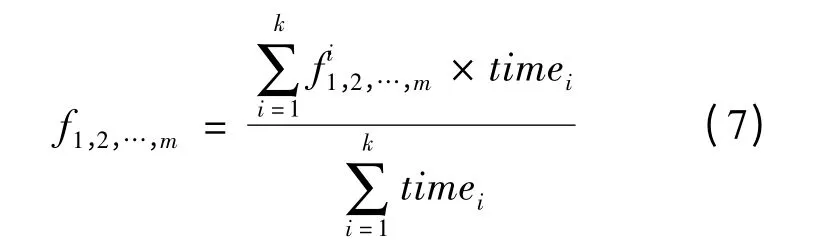
式中:f1，2，…，m表示模型第1，2，…，m 個參數的標定結果表示通過加速過程第i 段數據標定的模型第1，2，…，m 個參數。

由于數據段包含的時間越長，越能代表駕駛員的行為特征，所以在計算參數平均值時將第i段數據包含的時長timei作為該數據段標定參數的權重。根據相同方法對減速狀態和跟馳狀態數據的標定結果進行處理，得到矩陣BDac、BDdc和BDnor，分別為根據加速、減速和跟馳狀態數據得出的參數標定結果，對應的殘差平均值分別為1.9926×10－4、7.6433×10－4和4.2588×10－4。參數標定結果都為25×12 階矩陣，矩陣的每一行代表一個駕駛員的參數標定結果，第1 ～5 列分別對應OV 模型參數k、V1、V2，C1，C2;第6 ～12 列分別對應IDM 模型參數w、v0、δ，s0，s1，T，d。

2 基于跟馳數據的車輛和駕駛員特性分析

由于車輛和駕駛員具有個體特征，不同的駕駛員在車輛跟馳過程中采取的行為方式存在差異，反映到跟馳模型中，體現為模型的參數具有不同的取值。為了研究模型參數在不同車輛間的變化規律，對各個駕駛員的參數標定結果進行主成分分析、因子分析和相關分析，結果表明相關分析的效果較好，同一模型的參數間相關關系較為明顯，因此本文僅介紹相關性分析的過程:對BDac、BDdc和BDnor中的列向量進行相關分析，計算每兩個列向量間的相關系數，設有第i 列和第j 列參數向量，則相關系數的計算公式為:

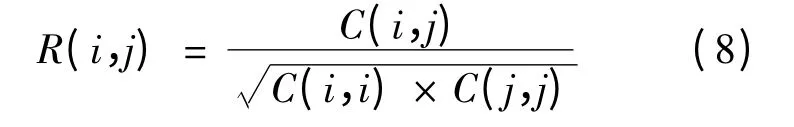
式中:C(i，j)為i，j 的協方差;R(i，j)為標準化的隨機向量和的協方差。

假設滿足相關系數R(i，j)＞0.7 或者R(i，j)＜－0.7 的向量是顯著相關的，考查BDac、BDdc和BDnor內模型不同參數間變化的相關性，得出如下結論:①不同模型的參數變化相關程度并不明顯;②同一模型內的參數變化有比較強的相關性。根據BDac得出，OV 模型中的參數V1和C1，V2和C2具有顯著相關性，IDM 模型中的參數δ、s1、d 具有顯著相關性;根據BDdc得出，OV 模型中的參數V2和C2具有顯著相關性，IDM 模型中的參數v0和s0，w、δ、s1、d 具有顯著相關性;根據BDnor得出，OV 模型中的參數V1和C1，V2和C2具有顯著相關性，IDM 模型中的參數v0和s0，δ、s1、d 具有顯著相關性。由于相關系數閾值取值較大，考慮到車輛行駛過程中隨機因素的影響，對在加速、減速或跟馳狀態中出現一次顯著相關的參數即認為其具有顯著相關關系。根據上述方法，OV 模型中的參數可根據相關情況分為3 組:k，V1和C1，V2和C2。其中V1和C1成負相關關系，而V2和C2成正相關關系。IDM 模型中的參數也可分為3 組:T，v0和s0，w、δ、s1、d。其中v0和s0，w、δ、s1、d 均成顯著的正相關關系。

在描述車輛跟馳狀態參數標定結果的矩陣BDnor中，模型參數在駕駛員間的變化情況如圖1和圖2 所示(考慮到圖形的直觀清晰，以兩個參數為一組作圖)。

圖1 OV 模型中顯著相關的參數Fig.1 Significantly related parameters in OV model

在OV 模型和IDM 模型中，參數都可以依據相關分析分為3 組。在不同駕駛員間，同一組內的參數有著高度相關的變化方式，而不同組間的參數變化相關關系并不顯著，因此本文假設三組參數分別對應車輛和駕駛員的三種特性，而不同的特性之間相互獨立。由于跟馳模型中，車輛的個體差異性完全由參數取值來體現，本文用三個相互獨立的因子來描述車輛與駕駛員在跟馳行為中的特性，稱這些因子為特征因子。相關分析表明特征因子對應的參數變化是高度相關的，考慮到判定顯著相關系數閾值取值較大、駕駛行為的隨機性和參數采集標定過程中產生的誤差，本文假設特征因子對應的相關參數間的變化方式是近似一致的(即參數的相關系數為1 或－1)，而不同特征因子對應的參數相互獨立。當參數列i，j的相關系數為1 或－1 時，標準化的隨機向量(i－和相等或互為相反數，據此提出特征因子的計算公式為:

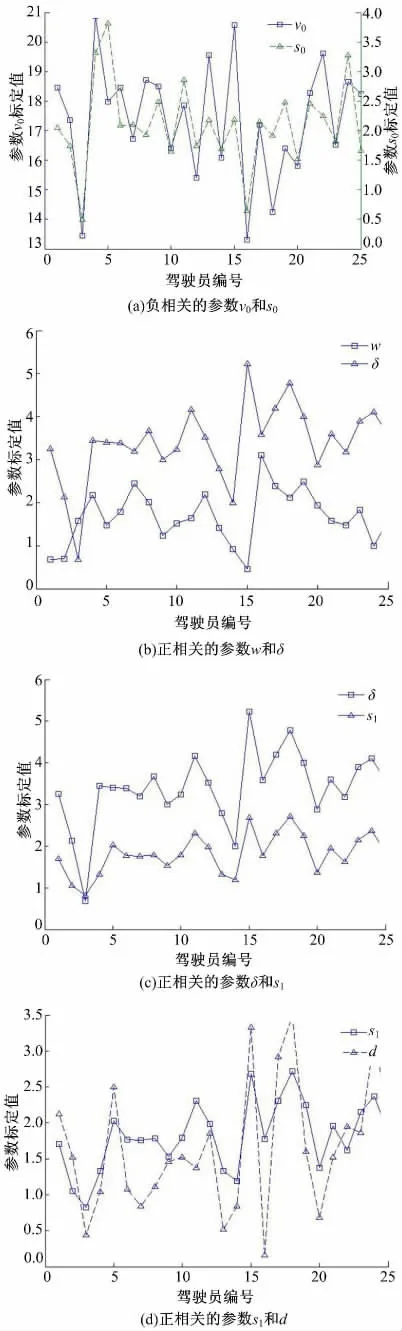
圖2 IDM 模型中顯著相關的參數Fig.2 Significantly related parameters in IDM model

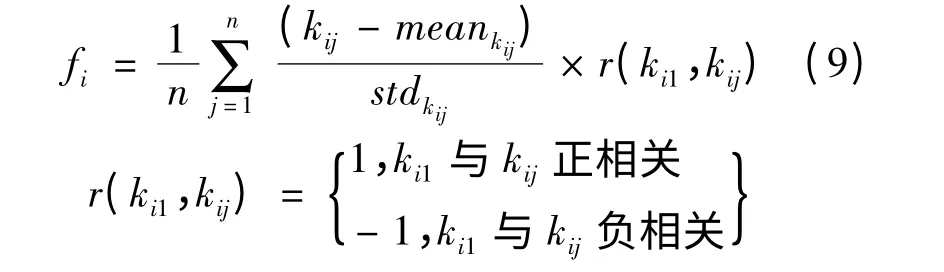
式中:fi表示由第i 組具有相關關系的參數所決定的特征因子;n 表示第i 組參數所包含的參數個數;kij為參數組i 中第j 個參數;meankij表示樣本數據中kij的均值;stdkij表示樣本數據中kij的標準差。

由式(9)可知:每個特征因子都是一個隨駕駛員編號變化的、標準化的隨機變量。特征因子和具有相關關系的參數組是一一對應的，在已知特征因子和參數在樣本中的均值和標準差的情況下，可以計算出具有相關關系的參數組中的參數值，方便特征因子在仿真過程中的應用。表1 給出了由描述車輛跟馳狀態的參數標定結果矩陣BDnor得出的特征因子取值，表中OV 模型的特征因子對應參數對應參數V1和對應參數V2和C2。IDM 模型的特征因子對應參數w、δ、s1、d對應參數v0、s0對應參數T。

由于OV 模型和IDM 模型的特征因子都可以完整地描述車輛和駕駛員的跟馳特性，可以設想，存在可逆的向量函數g，使得，以及，即不同模型的特征因子之間可以相互轉換，由于該轉換關系并沒有重要的實際應用意義，本文對其暫不進行深入研究。

IDM 模型的參數含義較為明確，因此根據IDM 模型的參數來考查該模型特征因子的實際意義。IDM 模型中與w、δ、s1、d 正相關，可見與車輛的加減速性能以及車輛在運動狀態中與速度有關的安全距離選取有較為重要的聯系，稱為動態特征因子;與v0和s0正相關，其中v0和s0都與車輛的運動狀態無關，因此稱為靜態特征因子;與參數T 正相關，稱為反應時間特征因子。

了解特征因子的意義后，可以通過特征因子的取值考查車輛和駕駛員的特性及其分布，如表1 中1 號駕駛員的動態特征因子為－0.3524，靜態特征因子為0.2339，反應時間特征因子為0.8704，可知該駕駛員駕駛的車輛加減速性能低于樣本平均水平，同時駕駛行為比較謹慎，在車輛靜止時采取較大的安全間距，在剎車時具有較長的反應時間。應當指出的是，不同模型得出的特征因子具有不同意義，對于某些模型，特征因子的含義也許難以表述，因此在研究車輛和駕駛員特性時，最好采用參數意義較為明確的模型進行標定和分析。通過對特征因子的分析可得出車輛及駕駛員的特性分布情況，由于條件所限，本文中數據樣本量較少，因此對數據樣本中車輛和駕駛員的特性分布暫不進行深入研究。

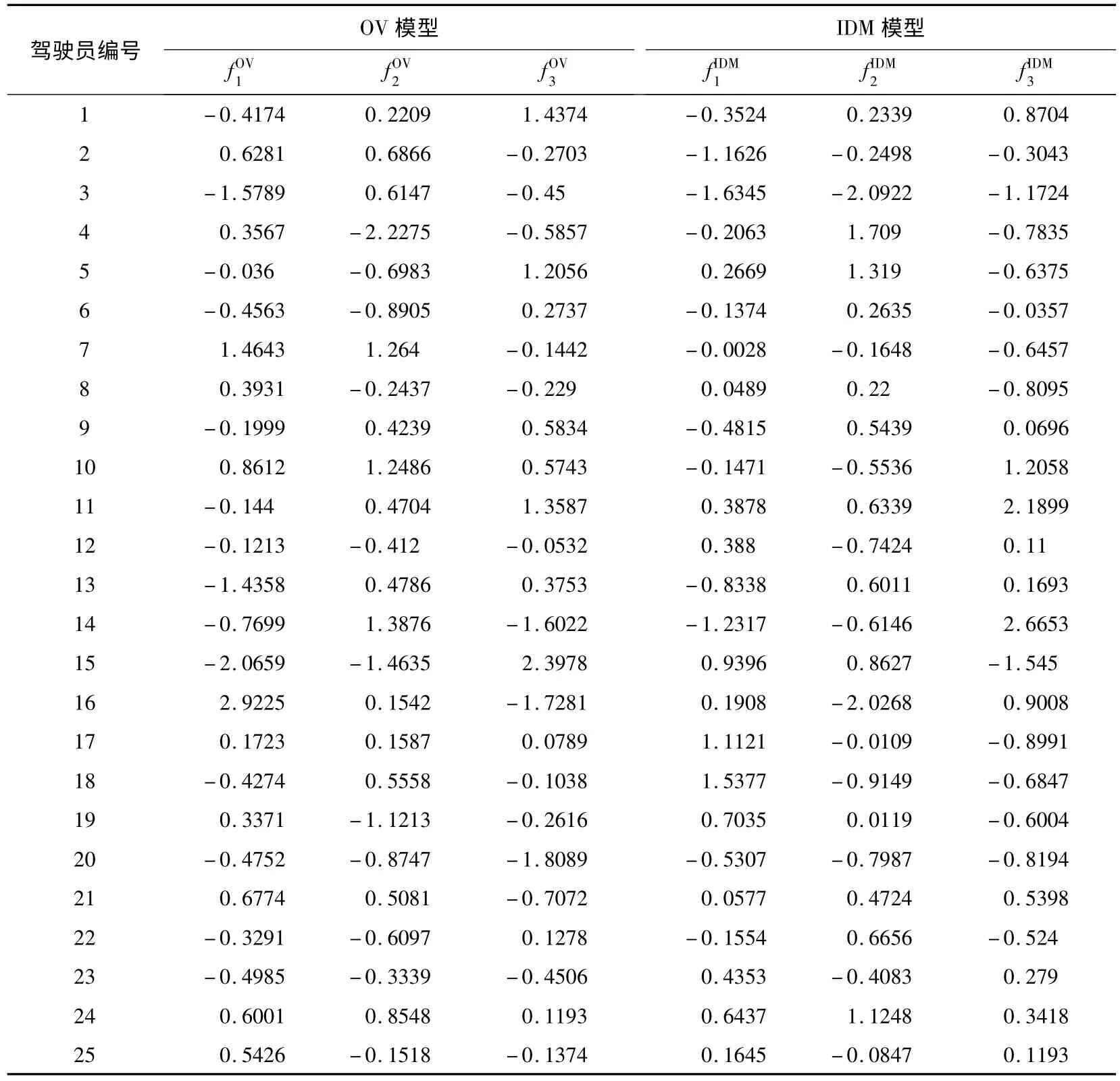
表1 OV 模型和IDM 模型中的特征因子取值Table 1 Characteristic factors in OV and IDM model

本文通過跟馳數據采集、數據處理和參數標定、參數相關性分析、特征因子計算、特征因子分布研究的步驟在跟馳數據基礎上對車輛和駕駛員特性進行分類和深入分析。當樣本的數據量較大時，可以根據特征因子的分布情況對樣本中車輛和駕駛員的特性分布進行研究。當車輛和駕駛員的特性分布情況已知時，可以通過特征因子和模型參數之間的換算將車輛特性體現在交通仿真中。

3 各異性IDM 模型及數值模擬

3.1 參數離散方法

根據第2 節中提出的車輛和駕駛員特性分析方法，在車輛和駕駛員的特性分布形式已知時，可以通過特征因子與模型參數之間的換算將車輛特性體現在交通仿真中。本文中數據樣本量較少，難以得出準確的車輛特性分布，因此在仿真中假設特征因子獨立服從標準正態分布的形式。

以IDM 模型為例，將特征因子與參數變化方式聯系起來，建立各異性跟馳模型。假設車輛的動態特征因子、靜態特征因子和反應時間特征因子在仿真對象中服從相互獨立的標準正態分布，則對于駕駛員i，模型各參數表達式為:

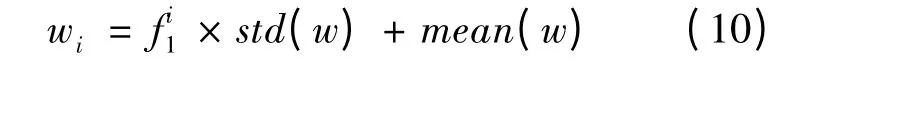
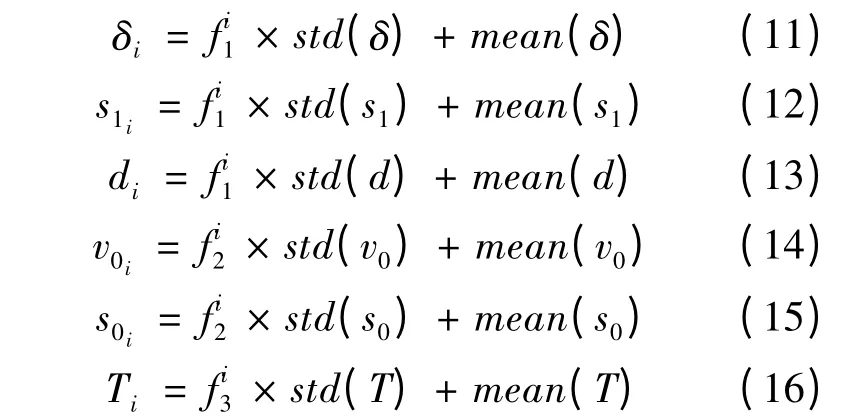
表2 IDM 模型參數的均值和標準差Table 2 Mean and standard deviation of parameters in IDM model

3.2 稠密交通流中擾動傳播的數值模擬

對稠密交通流中擾動傳播進行模擬，作如下假設:車隊由35 輛車組成，起始車頭間距為23 m，頭車初速度為12.2 m/s。頭車初始加速度為0，第6 ～7 s 加速度為－5.5 m/s2，第8 ～12 s 加速度為0，第13 ～14 s 加速度為4.25 m/s2，之后加速度恒為0，使得頭車速度由12.2 m/s 減為1.2 m/s，持續4 s 并重新加速至9.7 m/s，形成一個向后傳播的擾動。

采用各異性IDM 模型進行仿真，仿真開始時，每輛車的動態特征因子、靜態特征因子和反應時間特征因子分別由獨立服從標準正態分布的隨機數生成，根據特征因子通過式(10)～(16)計算該駕駛員-車輛單元的模型參數。通過多次模擬研究特征因子取值及分布對交通流狀態演變的影響，仿真結果如圖3 所示。

經典IDM 模型是確定性模型，同種初始條件下的模擬結果總是一致的;在參數取值相同的情況下，車輛在跟馳過程中會表現出相同的特性，時間位移曲線的線型會趨于一致。從圖中可看出，在各異性IDM 模型中，由于車輛和駕駛員的個體差異，其時間位移曲線呈現出不同的線型;隨著特征因子的不同取值和車輛及駕駛員特性在交通流中分布方式的差異，擾動在稠密交通流中的傳播會根據一定概率出現消散、穩定傳播、增大等不同情況。仿真結果說明，各異性IDM 模型可以描述在車輛及駕駛員特性的影響下，交通系統可能出現的不同演化情形，與實際交通情況相符合。

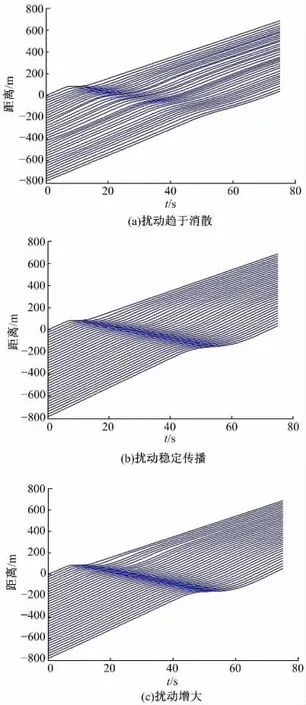
圖3 車輛及駕駛員特性對稠密交通流中擾動傳播的影響Fig.3 Influence of driver-vehicle characteristics on propagation of perturbations in dense traffic flow

4 結束語

提出了一種基于跟馳數據研究車輛和駕駛員特性的方法，方法步驟主要包括:跟馳數據采集-數據處理和參數標定-參數相關性分析-特征因子計算-特征因子分布研究。通過引入特征因子的概念，可以將車輛及駕駛員特性與模型參數取值有機聯系起來，實現基于跟馳數據的車輛特性描述和分析，以及基于車輛和駕駛員特性的交通仿真，提高了交通仿真與實測數據的契合程度。

以OV 和IDM 模型為例實現了該車輛特性分析方法。在江蘇省南京市進行跟馳數據采集，對OV 模型和IDM 模型進行參數標定。相關性分析表明:①不同模型的參數變化相關程度并不明顯;②同一模型內的參數變化有較強的相關性。根據相關分析的結果將兩種模型的參數分別分為3組，將每組高度相關的參數歸納為一個因子，計算出每個駕駛員-車輛單元的特征因子取值。由于本文采集的數據樣本量較少，因此沒有對車輛及駕駛員特性的分布形式進行深入研究。以IDM模型為例，假設車輛的3 個特征因子獨立服從標準正態分布，實現了基于車輛和駕駛員特性分析的交通仿真。仿真結果表明，各異性IDM 模型可以描述在車輛特性的影響下交通系統可能出現的不同演化情形，與實際交通情況相符合。

［1］Newell G F.A simplified car-following theory:a lower order model［J］.Transportation Research Part B，2002，36(3):195-205.

［2］Ahn S，Cassidy M J，Laval J.Verification of a simplified car-following theory［J］.Transportation Research Part B，2004，38(5):431-440.

［3］賈洪飛，雋志才，王曉原，等.利用因子分析選取車輛跟馳模型輸入變量［J］.公路交通科技，2004，21(1):81-84.Jia Hong-fei，Juan Zhi-cai，Wang Xiao-yuan，et al.Factor analysis for choosing input variables of car-following model［J］.Journal of Highway and Transportation Research and Development，2004，21(1):81-84.

［4］賈洪飛，雋志才，曹鵬.跟馳過程中駕駛員認知結構模型的建立［J］.公路交通科技，2005，22(11):130-132.Jia Hong-fei，Juan Zhi-cai，Cao Peng.A cognition structure model for drivers＇car-following behavior［J］.Journal of Highway and Transportation Research and Development，2005，22(11):130-132.

［5］王昊，王煒.各異性FVD 模型及數值模擬［J］.哈爾濱工業大學學報，2010，42(1):138-142.Wang Hao，Wang Wei.Heterogeneous FVD model and numerical simulation［J］.Journal of Harbin Institute of Technology，2010，42(1):138-142.

［6］敬明，鄧衛，劉志明，等.基于車輛個體特征的IDM模型研究［J］.交通信息與安全，2012，30(5):10-13.Jing Ming，Deng Wei，Liu Zhi-ming，et al.IDM model based on individual features［J］.Journal of Transport Information and Safety，2012，30(5):10-13.

［7］敬明，鄧衛.基于車輛個體行為的交通流跟馳模型研究［J］.交通科技，2008(6):84-87.Jing Ming，Deng Wei.Research on car following model that reflects individual differences［J］.Transportation Science＆Technology，2008(6):84-87.

［8］吳超仲，馬曉風，嚴新平.考慮駕駛員反應能力的跟馳模型［J］.武漢理工大學學報:交通科學與工程版，2007，31(4):630-632.Wu Chao-zhong，Ma Xiao-feng，Yan Xin-ping.Car following model based on drivers'reaction time［J］.Journal of Wuhan University of Technology(Transportation Science＆Engineering)，2007，31(4):630-632.

［9］Bando M，Hasebe K，Nakayama A，et al.Dynamical model of traffic congestion and numerical simulation［J］.Physical Review E，1995，51(2):1035-1042.

［10］Treiber M，Hennecke A，Helbing D.Congested traffic states in empirical observations and microscopic simulation［J］.Physical Review E，2000，62(2):1805-1828.

［11］Wang Hao，Wang Wei，Chen Jun.General Newell model and related second-order expressions［J］.Transportation Research Record，2011，2260:42-49.

［12］Herman R，Montroll E W.Traffic dynamics:studies in car following［J］.Operations Research，1958，6(2):165-184.

［13］廖惠紅，李丹，王昊，等.跟馳模型中反應延遲時間項作用機制的數值模擬［J］.交通信息與安全，2010，28(2):33-36.Liao Hui-hong，Li Dan，Wang Hao，et al.Numerical simulation of the perception/reaction delay time in carfollowing model［J］.Journal of Transport Information and Safety，2010，28(2):33-36.