四輪驅動電動汽車軸間驅動力和制動力分配

李 洋，張建偉，郭孔輝，武冬梅

(吉林大學 汽車仿真與控制國家重點實驗室，長春130022)

0 引 言

與傳統兩驅車輛相比，四輪驅動電動汽車前后軸的驅動力和制動力理論上可以任意分配，而不同的分配方式對車輛的動力學穩定性以及節能優化具有重要影響。已有暫時不考慮能量問題，從動力學穩定性角度進行研究的相關成果，如“I”曲線作為直線制動工況下的理想分配方式并被廣泛采用［1-2］，但“I”曲線是在車輪沒有產生側向力的前提下推導的，在車輛轉彎或受到干擾產生輪胎側向力時，并不能保證前、后軸車輪能同時達到附著極限，所以并不適用于車輛的整個行駛工況;文獻［3-6］以整車路面附著利用率最小為目標，進行驅動力和制動力的動態優化分配，這種方法可以保證車輛行駛時各個車輪總的路面附著利用率最小，具有較好的附著潛力，可以提高整車的穩定性，但這種方法需要利用輪胎側向力、路面附著系數、輪胎載荷、輪胎滑移率等車輛信息，容易受車輛狀態測量和估計精度的影響，在實際車輛系統中應用比較困難。

本文在考慮車輛側向穩定需求的基礎上，根據輪胎力的摩擦圓原理，以車輛前、后軸車輪同時達到附著極限、最大限度提高車輛的側向穩定性為目標。利用簡化的二輪車輛模型，通過理論推導得到四輪驅動電動汽車前、后軸驅動力和制動力的理想分配關系，并進行了仿真分析。

1 車輛簡化模型

由于只研究前、后軸的驅動力和制動力分配，所以將車輛模型簡化為二輪模型進行分析，考慮車輛沿X 軸的縱向運動和沿Y 軸的側向運動的兩個自由度，如圖1 所示。圖中:ax、ay分別為車輛的縱向、側向加速度;Fx1、Fx2分別為前、后軸的縱向力;Fy1、Fy2分別為前、后軸的側向力;a，b 分別為頂心到前軸和后軸的距離;L 為前軸和后軸之間的距離，L=a+b。

為了分析車輛主要參數和狀態的影響，作以下假設和簡化:行駛中質心的位置不變;縱向加速度由前后輪處產生的驅動力、制動力的和來決定;輪胎相對接地面總是直立狀態，輪胎摩擦圓的大小與載荷和路面摩擦因數的積成正比;側向加速度由前輪和后輪處產生的側向力的和決定，并且只考慮穩態情況下，所以前、后輪的側向力大小與其靜態載荷分布成比例。

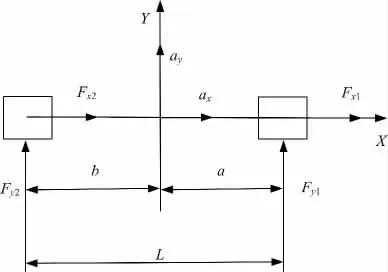
圖1 二輪車輛模型Fig.1 2-wheel vehicle model

車輛縱向和側向的動力學方程為:

式中:M 為整車質量。

根據以上假設，利用輪胎力的摩擦圓原理，車輛前、后軸車輪達到附著極限的條件分別為:

式中:μ 為路面附著系數;Fz10、Fz20分別為前、后軸的靜態載荷:

ΔFz為前、后軸的載荷轉移量:

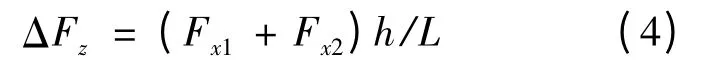
式中:h 為車輛的質心高度。

考慮穩態情況下，前、后輪的側向力關系與其靜態載荷分布關系相同，則有:

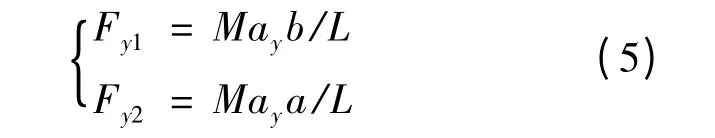
將載荷轉移量表達式(3)～式(5)代入式(2)，可得前、后軸同時達到附著極限的條件是:

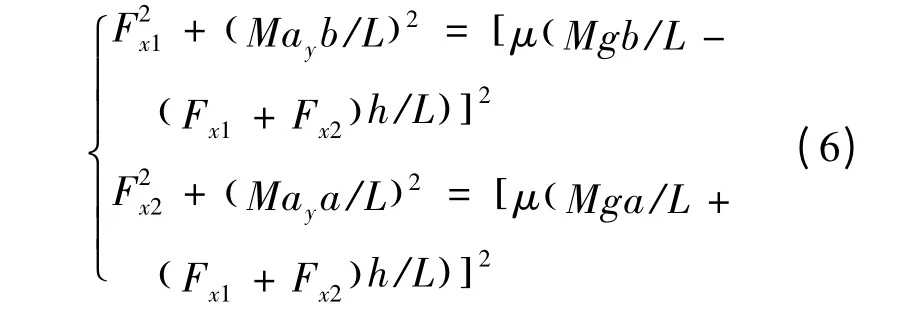
2 直線行駛時的擴展“I”曲線分配

如果只考慮直線行駛情況下，車輛沒有側向力需求，側向加速度可以認為是零，則前、后軸分別達到附著極限的條件可以寫成:

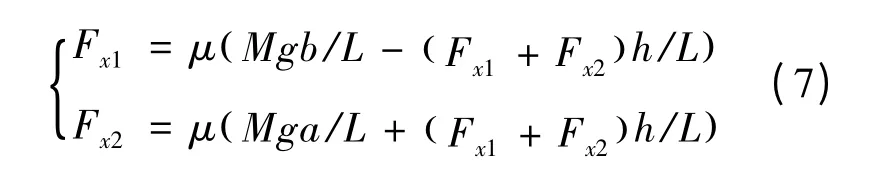
前、后軸驅動力和制動力的極限情況可以分為四種:驅動時前輪先達到附著極限;驅動時后輪先達到附著極限;制動時前輪先達到附著極限;制動時后輪先達到附著極限。考慮后兩種制動情況，根據式(7)可以畫出不同路面上的前、后軸驅動力和制動力的關系，如圖2 所示。由于只關注前、后軸力的分配比例，所以本文的驅動力和制動力都是與整車載荷的比值，是無量綱量。

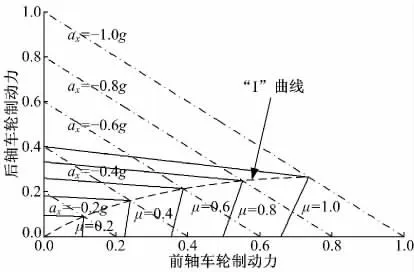
圖2 車輛直線制動時的“I”曲線Fig.2 “I”curve as braking in straight

圖2 中虛線為前輪達到附著極限和后輪達到附著極限的交點，即前、后軸同時達到附著極限的關系曲線，就是通常所說的“I”曲線。圖中一系列點劃線代表不同的縱向加速度，按“I”曲線進行制動力分配，在相同路面上，能夠使車輛達到最大的減速度。同時“I”曲線可以使前、后軸同時抱死，車輛會趨于中性轉向特性。

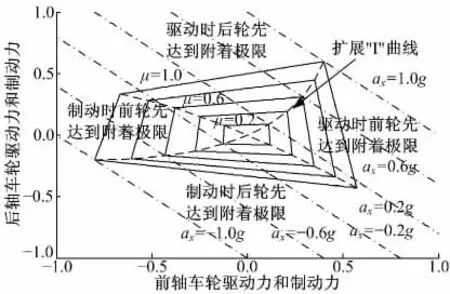
圖3 車輛直線驅動和制動時的擴展“I”曲線Fig.3 Extended“I”curve as driving and braking in straight

將驅動和制動4 種極限情況全部表示出來，如圖3 所示。圖3 中的四邊形為相同路面附著系數，從外向內路面附著系數逐漸減小，四條邊分別代表前面所說的4 種極限情況。虛線仍然是前、后軸同時達到附著極限的關系曲線，第3 象限就是制動時的“I”曲線，第1 象限則為驅動時的“I”曲線。第2 象限和第4 象限表示前后輪力矩方向相反的情況，在一些前后輪旋轉約束力強的4WD車上有時可能發生。本文只研究第1 象限和第3象限的情況，將這兩個象限內前、后軸同時達到附著極限的關系曲線統一稱作擴展“I”曲線。從圖3 中可以看出，按擴展“I”曲線進行驅動力和制動力的分配，在相同路面上，能夠使車輛達到最大的加速度和減速度。同時擴展“I”曲線可以使前、后軸同時滑轉或抱死，車輛會趨于中性轉向特性。

3 全工況下的理想分配方法

本節研究車輛在彎道行駛或受到側向干擾時，使前、后輪同時達到附著極限的理想分配方法。

根據式(6)，如果給定路面附著系數μ，則可以得到不同側向加速度需求ay下，前、后軸驅動力和制動力的關系。圖4(a)和圖4(b)分別為高附著路面μ=1.0 和低附著路面μ=0.3 時的理想分配關系圖。

圖4 高、低附著路面上的理想分配關系Fig.4 Ideal distribution on the high and low adhesion road

圖4 中的四邊形為相同最大側向加速度，從外向內最大側向加速度逐漸增大。與直線行駛時相同，圖中虛線B 為前、后軸車輪同時達到附著極限的關系曲線。可以看出，驅動時B 線有一部分延伸到了第2 象限，制動時也有一部分延伸到了第2 象限，尤其是高附著路面上更為明顯。以驅動時為例:B 線在第1 象限時，相同縱向加速度下，即在點劃線上，與B 線交點處的四邊形在最內側，所以能達到的側向加速度最大;而在相同側向加速度下，即同一個四邊形上，與B 線交點處的點劃線在最上側，所以能達到的縱向加速度最大。B 線在第2 象限時，Y 軸比B 線所處的四邊形更向內側，即按Y 軸分配能達到最大的側向加速度。同樣制動時，B 線在第2 象限時，按X 軸分配效果最好。

所以將圖中C 線作為理想分配曲線:驅動時按第1 象限B 線和相交后的Y 軸分配;制動時按第3 象限B 線和相交后的X 軸分配。可以使車輛達到最大的側向和縱向加速度，具有最好的極限性能。同時前、后軸能同時達到附著極限，車輛傾向于中性轉向，將具有良好的操縱特性。

為了求出前、后軸車輪直接的分配關系，便于在實際中的應用，定義后軸的分配比為:

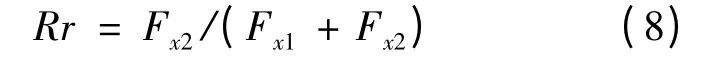
同時根據:

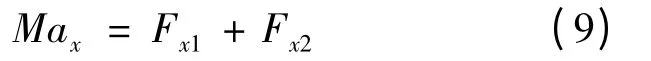
式(6)可以表示為:

式(10)中的M、a、b、L、h 都是容易獲得的車輛參數，需要的車輛狀態有μ、ax和ay，要求解的未知量是Rr。其中μ 是必需的，而ax和ay只需要其中一個就可以用式(10)中的兩個方程解出Rr。

根據對圖4 的分析可知:如果已知車輛的側向加速度ay，車輛在當前側向加速度下，可以達到最大的縱向加速度或減速度，縱向動力性能最佳;相反，如果已知車輛的縱向加速度ax，車輛在當前縱向加速度下，可以達到最大的側向加速度，側向穩定裕度最大，穩定性最佳。而無論直線行駛還是彎道行駛，車輛的側向穩定性都比縱向性能重要，應該優先得到保證。因此選擇根據當前車輛的縱向加速度需求來決策分配關系，使車輛在保證當前縱向加速度的前提下，能夠提供最大的側向穩定裕度。

根據式(10)，利用路面附著系數μ 和縱向加速度ax，求出后軸的驅動力和制動力的分配比Rr。ax可以通過縱向加速度傳感器測量得到，μ 需要進行估計，這里假設兩個狀態都是已知的。可以畫出不同路面附著系數下的后軸分配比Rr 與縱向加速度ax的關系圖，如圖5 所示。

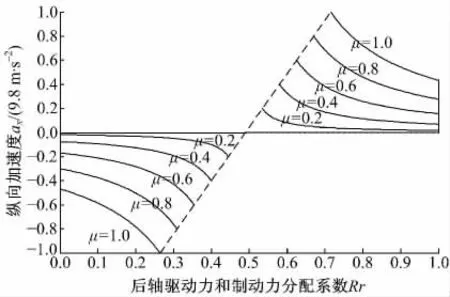
圖5 不同路面上的理想分配比Fig.5 Ideal distribution ratio on different road

從圖5 中可以看出，驅動時后輪分配較多，制動時前輪分配較多。這與驅動時載荷向后轉移，而制動時載荷向前轉移的趨勢是一致的。另外在驅動工況加速度較小時，尤其是在高附著路面上，Rr 為1，即驅動力全部分配給后輪，隨著加速度增加逐漸向前輪分配。而制動工況減速度較小時，Rr 為0，即制動力全部分配給前輪，隨著減速度增加逐漸向后輪分配。這與圖4 中C 線是一致的，即加速度較小時，就按坐標軸分配，驅動時全部分配給后輪，制動時全部分配給前輪。圖5 中的虛線為不同附著系數下的最大縱向加速度邊界線，由于受路面條件的約束，所能達到的最大縱向加速度也必須在相應的范圍內。

圖6 理想分配比的三維圖Fig.6 3D chart of ideal distribution ratio

為了進行實際應用，將分析出的理想分配方法做成三維圖表，如圖6 所示。根據路面附著系數和縱向加速度查表，可以實時動態分配前、后軸的驅動力和制動力。

4 仿真分析

為了進行仿真研究，建立了十自由度四輪驅動電動汽車車輛模型，包括車體模塊、電機模塊、電池模塊、制動模塊、輪胎模塊、車輪模塊、動態載荷模塊以及懸架K＆C 特性模塊等。利用所開發的車輛模型，對前、后軸驅動力和制動力的分配方法進行仿真分析。仿真車輛模型的相關參數設置如下:整車質量M 為1230 kg;質心至前軸距離a為1.1954 m;質心至后軸距離b 為1.2446 m;質心高h 為0.55 m。

為了進行對比分析，分別對僅前輪驅動和制動，僅后輪驅動和制動，前、后軸平均分配，按擴展“I”曲線進行分配和理想分配這5 種典型的驅動力和制動力分配方式進行了仿真。

4.1 側向穩定性仿真分析

車輛以恒定的加、減速度進行驅動或制動，方向盤固定，在車輛質心處施加一定強度的側向風干擾力，這時車輛就會產生抵抗干擾的側向力，如果側向力不足以抵抗干擾，就會產生橫擺，出現側向偏移。車輛所能產生的最大側向力越大，車輛抵抗干擾的能力越強，側向偏移越小。在相同縱向加速度下，不同分配方式的車輛能夠提供的側向力不同，側向偏移也就不同。對高、低附著路面不同工況下車輛的側向穩定進行仿真分析，結果如圖7 所示。

(1)高附著路面驅動工況:路面附著系數為0.8，縱向加速度約為0.25g，質心側向干擾力為3 kN，方向為車輛坐標系Y 軸正方向，仿真結果如圖7(a)(b)所示。從圖中可以看出，理想分配方式和僅后輪驅動的分配方式軌跡重合，偏移距離最小;其次是平均分配方式;擴展“I 曲線”分配方式比平均分配偏移稍大;僅前輪驅動的分配方式偏移最大。因此理想分配方式和后輪驅動分配方式能夠提供的側向力最大，即在車輛行駛過程中保留的側向穩定裕度最大，這兩種分配方式下的車輛側向穩定性最好。

設定縱向加速度約為0.25g，由前面理想分配方式的計算結果可知，這時后輪的分配比例為1，即是僅后輪驅動。因此，在高附著路面上車輛加速度不是特別大的情況下，理想分配方式基本與僅后輪驅動相同。

(2)高附著路面制動工況:路面附著系數為0.8，縱向減速度約為0.12g，側向風干擾力為2 kN，仿真結果如圖7(c)(d)所示。從圖中可以看出，理想分配方式和僅前輪制動的分配方式軌跡重合，偏移距離最小;其次是平均分配方式和擴展“I”曲線分配方式;僅后輪制動的分配方式偏移最大。因此高附著路面制動工況時，理想分配方式和僅前輪制動的分配方式的車輛側向穩定裕度最大。此時的縱向減速度較小，約為0.12g，后輪的分配比例為0，理想分配方式與僅前輪制動相同。

(3)低附著路面驅動工況:路面附著系數為0.3，縱向加速度約為0.1g，側向風干擾力為1 kN，仿真結果如圖7(e)(f)所示。從圖中可以看出，理想分配方式的車輛側向偏移距離最小;其次是平均分配方式和擴展“I 曲線”分配方式;僅后輪驅動的分配方式向反方向出現了較大偏移;僅前輪驅動的分配方式側向偏移最大。因此低附著路面驅動工況時，仍然是理想分配方式下的車輛側向穩定裕度最大。此時車輛加速度約為0.1g，理想分配算法決策出的前、后軸分配比，與僅后軸驅動的分配方式不再相同。

(4)低附著路面制動工況:路面附著系數為0.3，縱向減速度約為0.1g，側向風干擾力為2 kN，仿真結果如圖7(g)(h)所示。從圖中可以看出:依然是理想分配方式的車輛側向偏移距離最小;其次是僅前輪制動的分配方式;然后是擴展“I曲線”分配方式和平均分配方式;僅后輪制動的分配方式側向偏移最大。因此低附著路面驅動工況時，理想分配方式下的車輛側向穩定裕度也是最大。此時車輛減速度約為0.1g，理想分配算法決策出的前、后軸分配比，與僅前輪制動的分配方式不再相同。

在本節研究的各種工況中車輛的偏移方向不僅與側向風干擾力方向有關，還與前后輪的側滑順序有關:按車輛坐標系的定義，如果前輪先側滑則車輛會出現正方向的橫擺角速度，導致車輛向Y 軸正方向偏移，即與側向風干擾力方向一致;如果后輪先側滑則車輛會出現負方向的橫擺角速度，車輛向Y 軸負方向偏移，即與側向風干擾力方向相反。影響車輪側滑順序的主要因素是車輛的載荷轉移和驅動力、制動力的分配方式:車輪的載荷越小，分配的力越大，車輪越容易側滑;反之車輪載荷越大，分配的力越小，車輛越不容易側滑。本文的仿真工況中，由于各個工況中載荷轉移情況的不同和各種分配方法的不同，導致了車輪側滑順序和車輛側偏方向的不同。

圖7 車輛穩定性仿真結果Fig.7 Vehicle stability simulation results

4.2 操縱特性仿真分析

首先設定某個車速，車輛按固定方向盤轉角勻速行駛，計算此時的側向加速度，根據穩態情況下側向加速度ay與轉彎半徑R 的關系(見式(11))可以計算加速度為零時的轉彎半徑:

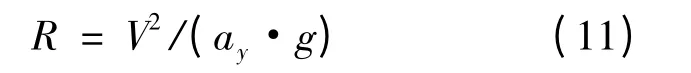
然后保持相同的方向盤轉角不變，使車輛以恒定加、減速度進行加速或減速，當車輛達到設定車速時，測量此時的瞬態側向加速度，便可以計算出當前加、減速度下車輛的轉彎半徑。車輛按不同的加、減速度行駛，便得到了轉彎半徑隨加、減速度的變化曲線如圖8 所示。轉彎半徑變化越小，車輛的操縱特性越好。

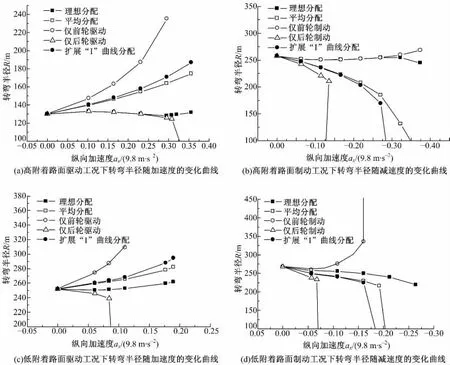
圖8 車輛操縱特性仿真結果Fig.8 Vehicle handling characteristic simulation results

(1)高附著路面驅動工況:路面附著系數為0.8，車速為60 km/h，方向盤轉角為20°，勻速時的側向加速度為0.218g，轉彎半徑為130 m。車輛以不同的加速度加速到60 km/h，轉彎半徑的變化特性如圖8(a)所示。從圖中可以看出，在加速度小于0.23g 左右時，理想分配方式與僅后輪驅動方式的轉彎半徑變化曲線相同，變化很小，當加速度大于0.23g 后，理想分配方式依然可以保持較小的變化，而僅后輪驅動方式在0.32g 后轉彎半徑急劇減小，車輛出現失穩。其他3 種分配方式的轉彎半徑隨著加速度的增加都迅速增大，其中平均分配變化較小，其次是擴展“I”曲線分配，變化最大的是僅前輪驅動的分配方式。因此在高附著路面驅動工況中，理想分配方式的轉彎半徑隨加速度的增加變化最小，車輛的操縱特性最好。

(2)高附著路面制動工況:路面附著系數為0.8，車速為60 km/h，方向盤轉角為10°，勻速時的側向加速度為0.11g，轉彎半徑為250 m。車輛以不同的減速度減速到60 km/h，轉彎半徑的變化特性如圖8(b)所示。從圖中可以看出:在減速度大于－0.27g 時，理想分配方式與僅前輪制動的轉彎半徑變化曲線相同，變化很小;當減速度小于－0.27g 后，理想分配方式的轉彎半徑開始緩慢減小，僅前輪制動的繼續增加。其他3 種分配方式的轉彎半徑隨著減速度的增加都迅速減小，其中平均分配變化較小，其次是擴展“I”曲線分配，變化最大的是僅后輪制動的分配方式。因此在高附著路面制動工況中，依然是理想分配方式的轉彎半徑隨減速度的增加變化最小，車輛的操縱特性最好。

(3)低附著路面驅動工況:路面附著系數為0.3，車速為40 km/h，方向盤轉角為10°，勻速時的側向加速度為0.05g，轉彎半徑為250 m。車輛以不同的減速度減速到40 km/h，轉彎半徑的變化特性如圖8(c)所示。從圖中可以看出:理想分配方式與僅后輪驅動方式的結果明顯不同，理想分配方式的轉彎半徑緩慢增加，變化很小，而僅后輪驅動方式先是逐漸減小，在0.08g 左右后轉彎半徑急劇減小，車輛出現失穩。其他3 種分配方式的轉彎半徑隨著加速度的增加都迅速增大，其中平均分配變化較小，其次是擴展“I”曲線分配，變化最大的是僅前輪驅動的分配方式。因此，在低附著路面驅動工況中，依然是理想分配方式的轉彎半徑隨加速度的增加變化最小，車輛的操縱特性最好。

(4)低附著路面制動工況:路面附著系數為0.3，車速為40 km/h，方向盤轉角為10°，勻速時的側向加速度為0.045g，轉彎半徑為250 m。車輛以不同的減速度減速到40 km/h，轉彎半徑的變化特性如圖8(d)所示。從圖中可以看出，理想分配方式與僅前輪制動方式的結果明顯不同，理想分配方式的轉彎半徑隨減速度增加緩慢減小，而僅后輪驅動方式先是逐漸減小，在－0.06g 左右以后轉彎半徑急劇增大，車輛出現失穩。其他3 種分配方式的轉彎半徑隨著減速度的增加都迅速減小，平均分配方式的轉彎半徑減小較慢，其次是擴展“I”曲線分配，僅前輪驅動的分配方式的轉彎半徑迅速增大。因此在低附著路面制動工況中，理想分配方式的轉彎半徑隨減速度的增加變化最小，車輛的操縱特性最好。

5 結 論

從動力學穩定性的角度出發，根據輪胎摩擦圓原理，以前、后軸車輪同時達到附著極限為目標，推導出前、后軸驅動力和制動力的理想分配關系。利用四輪驅動電動汽車車輛模型進行了仿真分析，通過與其他典型分配方式的對比可以得出以下結論:

(1)在高、低附著路面上的驅動和制動工況中，與其他典型分配方式相比，本文所研究的四輪驅動電動汽車前、后軸驅動力和制動力理想分配方法，都可以使車輛在保證當前縱向加速度的前提下，保持最大的側向穩定裕度，具有最好的側向穩定性。

(2)理想分配方式下，車輛轉彎半徑隨著加速度和減速度的增加變化最小，具有良好的操縱特性。

(3)本文研究的理想分配方法計算簡單，對車輛狀態信息的依賴程度小，便于在實際四輪驅動電動汽車控制系統中應用。

［1］鄭宏宇，許文凱，劉宗宇，等.四輪獨立驅動電動汽車再生制動控制策略［J］.吉林大學學報:工學版，2013，43(3):590-594.Zheng Hong-yu，Xu Wen-Kai，Liu Zong-yu，et al.Control strategy for regenerative braking for four-wheel-drive electric vehicle［J］.Journal of Jilin University(Engineering and Technology Edition)，2013，43(3):590-594.

［2］孫大許，蘭鳳崇，陳吉清.基于I 線制動力分配的四驅純電動汽車制動能量回收策略的研究［J］.汽車工程，2013，35(12):1057-1061.Sun Da-xu，Lan Feng-chong，Chen Ji-qing.A study on the braking energy recovery strategy for a 4WD batter electric vehicle based on ideal braking force distribution(Curve I)［J］.Automobile Engineering，2013，35(12):1057-1061.

［3］Ono E，Hattori Y，Koibuchi K.Vehicle dynamics integrated control for four-wheel-distributed steering and four-wheel-distributed traction/braking system［J］.Vehicle System Dynamics，2006，44(2):139-151.

［4］Mokhiamar O，Abe M.How the four wheels should share forces in an optimum cooperative chassis control［J］.Control Engineering Practice，2006，14(3):295-304.

［5］鄒廣才，羅禹貢，李克強.四輪獨立電驅動車輛全輪縱向力優化分配方法［J］.清華大學學報:自然科學版，2009，49(5):111-115.Zou Guang-cai，Luo Yu-gong，Li Ke-qiang.Tire longitudinal force optimization distribution for independent 4WD EV［J］.Journal of Tsinghua University(Science and Technology)，2009，49(5):111-115.

［6］余卓平，蔣煒，張立軍.四輪輪轂電機驅動電動汽車扭矩分配控制［J］.同濟大學學報:自然科學版，2008，36(8):1115-1119.Yu Zhuo-ping，Jiang Wei，Zhang Li-jun.Torque distribution control for four wheel in-wheel-motor electric vehicle［J］.Journal of Tongji University(Natural Science)，2008，36(8):1115-1119.