利用坐標平移與坐標旋轉方法的宏程序應用

□ 李雅昔 □ 李曉莉 □ 李星恕

1.商洛職業技術學院 陜西商洛 726000

2.西北農林科技大學 機電學院 陜西楊凌 712100

3.長安大學 信息工程學院 西安 710064

機械加工中經常遇到非圓曲線 （如橢圓曲線［1、2］、拋物線［3、4］、雙曲線［5］和漸開線等）零件，隨著產品性能要求的不斷提高，非圓曲線零件的作用日益重要，其加工質量往往成為產品制造的關鍵。數控機床的數控系統一般只具有直線插補和圓弧插補功能，并不具備此類非圓曲線的插補功能，采用普通的手工編程方法幾乎不可能完成這些輪廓的加工。若采用軟件自動編程，生成的程序往往很復雜，且缺乏靈活性和通用性。通過宏程序編程可以實現普通編程難以實現的功能，且編寫的程序具有極好的易讀性、修改性和通用性。機床在執行宏程序時，相比執行CAM軟件生成的程序更加快捷，反應更迅速。

本文以華中世紀星HNC-21T數控車削系統為例，借助坐標系平移［6、7］與坐標系旋轉［8、9］的方法，對數控車床加工任意位置非圓曲線回轉面的宏程序編寫方法進行分析。

1 利用坐標平移與坐標旋轉的方法在工件坐標系中建立非圓曲線方程

在實際加工中，工件坐標系原點常與待加工的非圓曲線方程所在坐標系原點不重合［10、11］，因此要找出兩個坐標系之間的關系，以便于在工件坐標系中重新建立非圓曲線方程。由于數控車床的輪廓設在XOZ平面上，給定非圓曲線方程所在坐標系中任意一點的坐標通過坐標平移與坐標旋轉的方法，可以在工件坐標系中得到相應的新坐標。而數控車床沒有坐標平移與坐標旋轉指令，所以必須對不同坐標系中的非圓曲線方程進行相應的數學處理。

1.1 坐標平移法

當待加工非圓曲線給定方程的坐標系X1O1Z1與數控車床工件坐標系XOZ僅存在平移關系時，可通過坐標平移的方法建立這兩個坐標系之間的關系。如圖1所示，工件坐標系為XOZ，待加工非圓曲線給定方程的坐標系為X1O1Z1。假定A點在X1O1Z1坐標系中的坐標為（x1，z1）,工件坐標系XOZ的原點O在坐標系X1O1Z1中的坐標為 （i，k）， 通過式（1）建立兩坐標系之間的關系，可將X1O1Z1坐標系中的A點坐標（x1，z1）轉換為數控車床工件坐標系 XOZ 中 A點坐標（x，z）。

▲圖1 坐標系平移

▲圖2 坐標系旋轉

▲圖3 坐標系平移與旋轉

1.2 坐標旋轉法

當待加工非圓曲線給定方程的坐標系X1O1Z1與數控車床工件坐標系XOZ僅存在旋轉關系時（即兩坐標系坐標原點重合），可通過三角函數關系建立這兩個坐標系之間的關系。如圖2所示，假定A點在原坐標系 X1O1Z1中的坐標為（x1，z1）,線段 OA 與 Z1軸的夾角為 α，則：

當原坐標系X1O1Z1繞坐標原點O1順時針方向旋轉角度θ后與工件坐標系XOZ重合時，點A在工件坐標系XOZ中的坐標為（x，z）。OA與Z軸的夾角為（αθ），可得：

由三角函數的運算法則可得A點在工件坐標系XOZ中的坐標值為：

當原坐標系X1O1Z1繞坐標原點O逆時針方向旋轉角度θ后與工件坐標系XOZ重合時，A點在工件坐標系XOZ中的坐標值為：

1.3 同時使用坐標平移法與坐標旋轉法

當待加工非圓曲線給定方程的坐標系X1O1Z1與數控車床工件坐標系XOZ既存在坐標系平移又存在坐標系旋轉時，可先按坐標系旋轉進行分析，再按坐標系平移進行分析，建立這兩個坐標系之間的關系。如圖3所示，坐標系X2O2Z2與坐標系X1O1Z1僅存在旋轉關系，同時坐標系X2O2Z2與工件坐標系XOZ僅存在平移關系，且工件坐標系原點O在坐標系X2O2Z2中的坐標為（i，k）。 假定 A 點在 X1O1Z1中的坐標為（x1，z1）, 由式（4）、（5）可得出 A 點在坐標系 X2O2Z2中的坐標（x1cosθ?z1sinθ，z1cosθ±x1sinθ） , 由式 （1） 可得 A 點在工件坐標系XOZ的坐標值：

式（6）中正負號的規定與式（4）、式（5）中正負號的規定相同。

2 車削非圓曲線輪廓宏程序編程思路

2.1 宏程序簡介

使用變量編寫可進行算術或邏輯運算，并能控制程序段流向的程序，稱為用戶宏程序。華中世紀星HNC-21T數控車削系統為用戶配備了類似于高級語言的宏程序功能，用戶可以使用變量進行算術運算、邏輯運算和函數的混合運算，此外宏程序還提供了循環語句、分支語句和子程序調用語句，利于編制各種復雜的零件加工程序，減少乃至免除手工編程時進行繁瑣的數值計算，精簡程序量。常用的語句主要有以下兩種。

（1）條件判別語句。

格式1：IF（條件表達式）… ELSE… ENDIF

格式2：IF（條件表達式）… ENDIF

（2）循環語句。

格式：WHILE（條件表達式）…ENDW

2.2 公式表達非圓曲線宏程序編制的一般步驟

（1）在工件坐標系XOZ中建立待加工非圓曲線的表達式，選定自變量并確定自變量的取值范圍。根據給定的非圓曲線方程進行坐標系平移或坐標系旋轉，將待加工非圓曲線方程轉變為工件坐標系XOZ中新的表達式。選擇合適的自變量來表示曲線上各關鍵點的坐標表達式，這一點在宏程序的編寫過程中尤為重要。自變量的選擇一般根據曲線方程方便情況來選定，自變量選定后，還需進一步確定其取值范圍。

（2）選擇擬合方式并確定自變量的步距。選擇擬合方式，即選擇采用直線段還是圓弧段來擬合非圓曲線。在確定自變量的步距時，一般根據所用機床的性能和工藝裝備，確定自變量的步距。步距取值越小，輪廓表面的擬合誤差越小，加工精度越高，但加工效率很低。步距取值越大，輪廓表面的擬合誤差越大，加工精度越低，但加工效率很高。一般情況下，自變量的步距取 0.05～0.2 mm。

（3）自變量的賦值與加工的終點判別。給定自變量的初值與終值，機床每移動一個步距后，自變量遞變，根據加工終值判別條件，與加工終值進行判別，當條件不滿足（即未加工到非圓曲線終點）時，執行新的步距，繼續循環加工，當條件滿足（即加工到非圓曲線終點）時，完成非圓曲線輪廓的加工，退出循環。非圓曲線輪廓數控加工流程圖如圖4所示。

▲圖4 橢圓輪廓數控加工流程圖

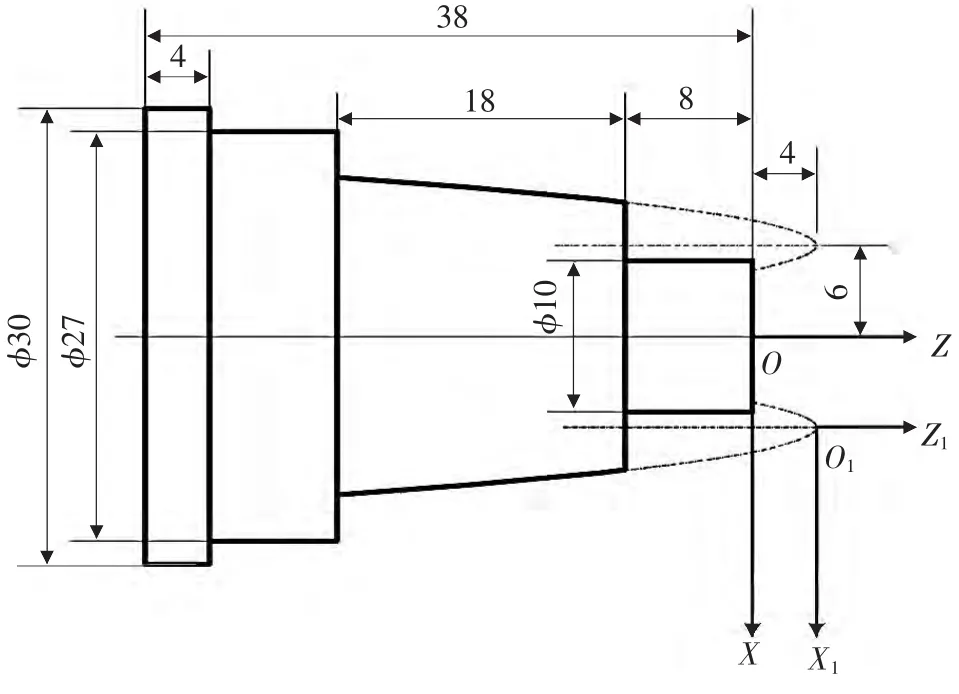
▲圖5 平移關系的零件加工圖

▲圖6 數控仿真結果

（4）編寫程序。因為一般毛坯存在較大的加工余量，故一般需采用粗車循環指令［12］與宏程序嵌套［13、14］的方法編寫程序。

3 非圓曲線輪廓宏程序編寫實例

3.1 僅存在平移關系時的宏程序編寫方法

零件加工圖如圖5所示，工件坐標系XOZ的原點為φ10 mm圓柱右端面中心，與給定拋物線方程的坐標系X1O1Z1的原點不重合，工件坐標系原點O在原坐標系 X1O1Z1中的坐標為（-6，-4），根據式（1），可以得出此時在工件坐標系XOZ中拋物線表達式為：z-4=-1.5（x-6）2，因 z的取值范圍容易確定，故取 z為自變量，在工件坐標系XOZ中，建立待拋物線方程：x=6+，其中自變量z的初值為-8，終值為-26。

根據上述數學分析，編寫待加工非圓曲線的宏程序，其子程序如下：

%0003

#5=-1.5 //拋物線方程系數賦值

#6=-8 //自變量z的初始值賦值

#7=-26 //自變量z的終止值賦值

WHILE#6 GE#7//建立循環條件：判斷自變量z是否達到加工終值-26

#8=6+SQRT［ ［#6-4］/#5］ //給因變量 x 賦值，即

G01 X［2*［#8］］ Z［#6］ F0.2//小段直線插補，逼近拋物線輪廓

#6=#11-0.05 //z步進為0.05，自變量遞減

ENDW

M99

數控仿真加工結果如圖6所示。

3.2 平移關系、旋轉關系并存時的宏程序編寫方法

零件加工圖如圖7所示，待加工非圓曲線（橢圓）在坐標系X1O1Z1中的方程為：。 因下側待加工橢圓的x值均為負值，故原橢圓方程可用方程x來表示,由式（6）可得待加工橢圓輪廓在工件坐標系XOZ中的坐標值為：

借助各種繪圖軟件，可方便地捕捉待加工斜橢圓自變量z1初值為15.008，終值為-19.890，在工件坐標系XOZ中相應的自變量z初 值 為 0， 終 值 為-31.799。

▲圖7 平移、旋轉關系的零件加工圖

▲圖8 數控仿真結果

編寫宏程序，其子程序如下：

%0005

#10=15 //短半軸賦值

#11=25 //長半軸賦值

#13=0 //在工件坐標系中，z的初值

#14=-31.799 //在工件坐標系中，z的終值

#15=-11.996 //在原方程坐標系中，x1的初值

#16=15.008 //在原方程坐標系中，z1的初值

WHILE#13 GE［#14］//建立循環條件：判斷自變量z是否達到加

工終值-31.799

#17=-［#10］*SQRT［1-#16*#16/#11/#11］ //在原坐標系中，計算變量x1，x1由方程 x1=-15×確定

#18=#17*cos［20*PI/180］-#16*sin［20*PI/180］+20//工件坐標系中，變量x的函數計算

#13=#16*cos［20*PI/180］+#17sin［20*PI/180］-10 //工件坐標系中，變量z的函數計算

#20=2*#18//工件坐標系中，變量x2為直徑編程

G01 X［#20］ Z［#13］ F0.2 //擬合加工，小段直線插補，逼近橢圓

輪廓

#16=#16-0.05//原坐標系中，自變量z1遞減變化步長ENDW

M99

數控仿真加工結果如圖8所示。

4 結束語

本文通過數學建模（坐標系平移與坐標系旋轉）的方法，將任意位置非圓曲線方程所在的坐標系與數控車床的工件坐標系建立聯系，以拋物線、橢圓為例，結合車削復合循環指令，借助本文坐標系平移與坐標系旋轉的結果，編寫了簡捷有效的宏程序，并通過數控仿真加工與實際加工，驗證了程序的正確性和可行性。

文中坐標系平移與坐標系旋轉的方法，對各類非圓曲線、不同位置的非圓曲線車削加工編程均具有借鑒作用。

［1］ 王西建,冀勉.宏程序在非圓曲線輪廓車削加工中的應用［J］.組合機床與自動化加工技術,2013（7）:110-111.

［2］ 何玉山.數控車床加工非圓曲線宏程序編寫技巧［J］.CAD/CAM與制造業信息化,2009（10）:88-89.

［3］ 岳秋琴.宏程序在非圓曲線數控車削加工中的應用［J］.煤礦機械,2013,34（7）:131-133.

［4］ 呼剛義,劉振.基于華中數控車宏程序的橢圓輪廓“插補指令”構建與實現［J］.制造業自動化,2008,34（5）:35-36.

［5］ 孟生才.數控車床宏程序在不同系統循環中的應用［J］.金屬加工（冷加工）,2010（22）:66-68.

［6］ 葉海見.斜橢圓宏程序在數控車床上的應用［J］.機床與液壓,2009,37（1）:194-195.

［7］ 賈春揚,杜海清.用于斜橢圓車削的模塊化宏程序開發［J］.輕工機械,2012,30（5）:84-85.

［8］ 王紅梅,王文友,葛曉陽.利用數控車床加工橢圓曲線的方法［J］.機床與液壓,2012,40（22）:13-14.

［9］ 陳銀,黃俞淇.巧用宏程序實現旋轉加工功能［J］.金屬加工（冷加工）,2012（22）:60-61.

［10］曹智梅.數控車床曲線方程的宏程序編制［J］.機床與液壓,2012,40（14）:141-143.

［11］薛明,趙薇.基于數控車削非圓二次曲線零件加工的研究［J］.組合機床與自動化加工技術,2013 （4）:129-131.

［12］王鋒波,孫士彬.FANUC系統宏程序在拋物線類零件中的應用［J］.煤礦機械,2011,32 （10）:148-150.

［13］韓全立,王宏穎.宏程序在數控編程中的應用技巧及編程實例［J］.機床與液壓,2010,38（12）:29-32.

［14］霍蘇萍,張月樓.宏程序在數控加工中的應用分析［J］.煤礦機械,2007,28（9）:121-123.