直線特征測量數據的平滑去噪*
□ 馮興輝 □ 張 旭 □ 陳禮貴 □ 宋 杰
上海工程技術大學 機械工程學院 上海 201620
直線特征測量數據的平滑去噪*
□ 馮興輝 □ 張 旭 □ 陳禮貴 □ 宋 杰
上海工程技術大學 機械工程學院 上海 201620
在逆向工程中,二維截面數據的重構是曲面重構的基礎,為得到擬合精度較高的截面曲線,需對所測數據進行處理。針對直線段離散數據,先利用均值平滑處理方法對其進行平滑去噪,再利用最小二乘法擬合出精度較高的直線,實例證明該平滑方法可行有效。
直線 離散數據 均值平滑 去噪
在逆向工程中,二維截面數據的重構是曲面重構的基礎,其重構的精確與否、質量好壞直接關系到三維重構模型外觀重現及功能復原效果的優劣。截面幾何特征一般由直線段、圓弧段和自由曲線段這些不同類型的曲線段拼接而成,直線作為二維截面特征之一,其重構精度的高低至關重要。由測量設備獲取的截面離散數據點,其精度受到產品制造誤差、測量誤差等影響,通常與理論點具有一定的偏差,根據這些具有偏差的數據擬合直線,其精度通常不夠理想。為擬合出精度較高的直線,筆者先利用均值平滑處理方法對測量的直線段數據進行平滑去噪,再利用最小二乘法擬合出精度較高的直線,實例證明該平滑方法可行有效。
1 均值平滑去噪
由測量設備獲取的截面離散數據點,通常與理論點存在一定的偏差,為了減少偏差,首先應對離散數據進行平滑去噪。均值平滑處理[1]是目前常用的一種方法,算法簡單,平滑效果明顯。均值平滑的主要目的是:改變由測量設備獲得的截面離散數據點的位置,使其盡可能減少與理論點的誤差,以便能夠重構出精度較高的直線。均值平滑公式[2]為:
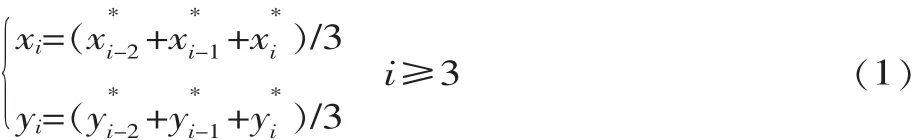
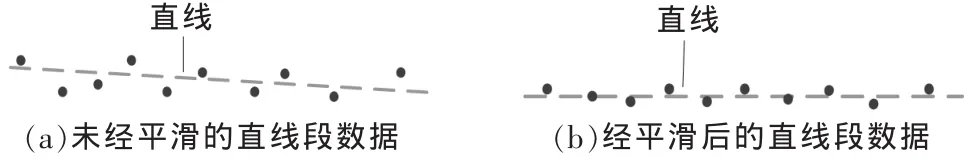
▲圖1 直線段數據平滑前后的變化
2 直線的重構
目前,在諸多試驗和工程實際問題中都會遇到直線擬合問題,其本質為:對于給定的n個測量點[(xi,yi),i=0,1,...,n]來尋找一條最佳的擬合直線,使其盡可能通過或靠近這些點。擬合的實質是求直線參數斜率和截距的最佳估計,擬合方法通常是采用最小二乘法[3]來求解擬合參數,該方法簡單實用,應用廣泛。直線的解析表達式[4]為:

式中:l0、l1、l2為直線方程的未知系數。
點到直線的有向代數距離d=l0x+l1y+l2,點到直線的歐氏距離[5]為:
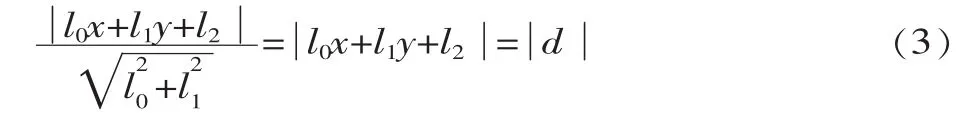
直線最小二乘擬合的目標函數[6]:
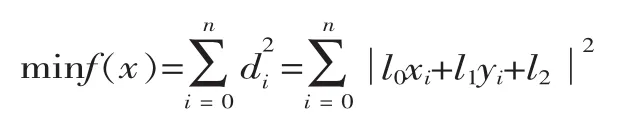
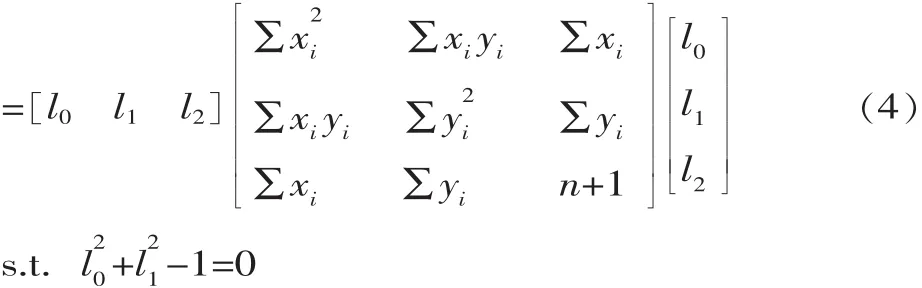
式中:di為各個數據點到直線的有向代數距離。
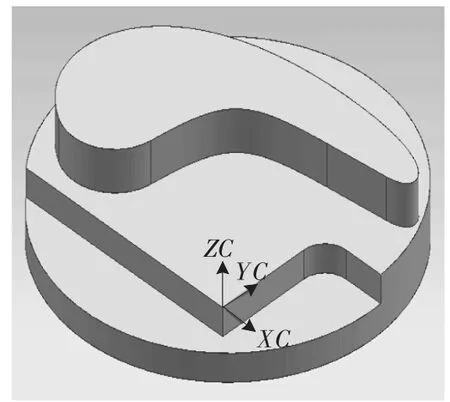
▲圖2 UG NX8.5設計的模型圖

▲圖3 實際加工和測量的工件
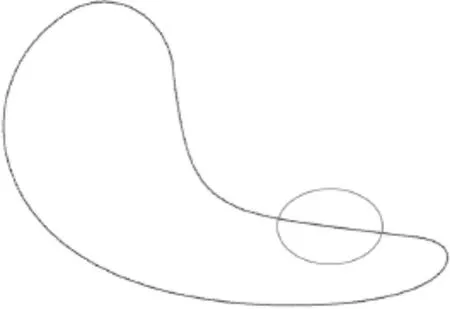
▲圖4 三坐標測量的全部點云數據
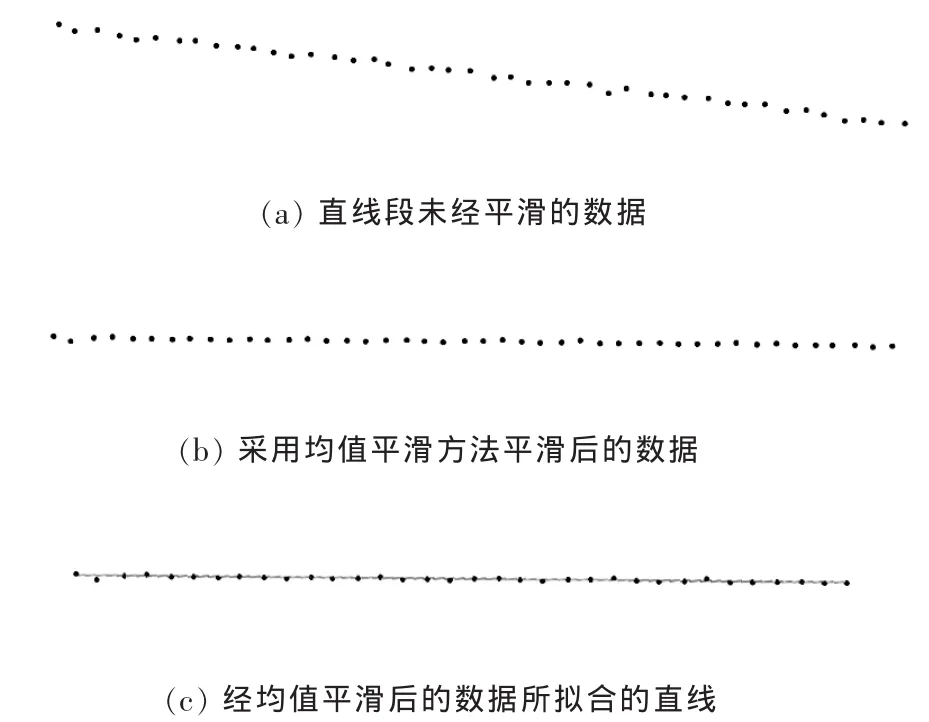
▲圖5 直線段數據的平滑與重構

▲圖6 未經平滑處理的數據所擬合的直線
3 實例分析
為有效檢驗該方法的可行性,先利用UG NX8.5設計包含各種截面線的模型,如圖2所示,再加工得到實際模型,如圖3所示,最后利用三坐標測量機測量得到各點坐標(采樣密度為0.5),點云數據如圖4所示。
具體操作方法是:首先利用本文方法對直線段數據進行均值平滑,然后再利用最小二乘法擬合平滑后的數據,平滑與擬合的具體情況如圖5所示,其中,圖5(a)表示未經平滑的直線段數據放大圖,圖5(b)表示利用均值平滑方法處理后的直線段數據,圖5(c)表示利用均值平滑方法后直線段數據所擬合的直線。
同時,為了對均值平滑的方法進行有效性檢驗,本文又對原始數據即未經均值平滑方法處理的直線段數據,利用最小二乘法進行擬合,并計算每個數據點到擬合直線的距離,圖6所示為未經平滑的直線段數據所擬合的直線。
為了檢驗經平滑后所擬合直線的精度,比較平滑前后每個數據點到所擬合直線的距離,并將其作為評判擬合精度的標準,具體結果見表1。

表1 平滑前后結果對比
由表1可知,平滑后所有數據點到所擬合直線的距離有明顯改善,平滑效果明顯,重構直線精度提高。
4 結論
本文主要針對截面數據為直線段的情況,對由三坐標測量所得的數據利用均值平滑方法進行處理,有效地減少了與理論數據的誤差,從而在接下來直線的重構過程中,可以擬合出精度較高的直線,同時也較好地反映了工件的原始特征信息。
[1]李家才.反求工程中一種數據平滑的方法[J].機械電子,2005(11).
[2]朱炬波,冉承其,賀明科.匹配數據的平滑濾波技術[J].中國空間科學技術,2002(4).
[3]李增兵,張曉帆,李瑞華,等.直線擬合快速實現的一種新算法[J].計算機測量與控制,2006,14(11):1524-1525.
[4]丁克良,沈云中,歐吉坤.整體最小二乘法直線擬合[J].遼寧工程技術大學學報,2010,29(1):44-47.
[5]田垅,劉宗田.最小二乘法分段直線擬合[J].計算機科學,2012,39(6A).
[6]徐海濤,高彩霞.直線擬合算法 [J].電腦知識與技術,2009,5(4):864-867.
(編輯 禾 禾)
TH123+.1;O212.1
B
1000-4998(2015)04-0071-02
*大學生科研訓練計劃資助項目(編號:HZJYKY20140001)
2014年10月

