圓、橢圓、三角形的一個相關性質的證明

●蔡玉書 (蘇州市第一中學 江蘇蘇州 215006)

?

圓、橢圓、三角形的一個相關性質的證明

●蔡玉書 (蘇州市第一中學 江蘇蘇州 215006)

2009年東南地區數學奧林匹克競賽有一道平面幾何試題如下：

例1 如圖1，已知⊙O,⊙I分別是△ABC的外接圓和內切圓，證明：過⊙O上任意一點D，都可以作一個△DEF，使得⊙O,⊙I分別是△DEF的外接圓和內切圓.

圖1

《數學通報》2011年第6期徐道老師利用解析法證明了命題1：

《數學通報》2011年第10期“對一道例題的探求與發現”中研究了這樣的試題：

例2 已知P，Q，R為拋物線y=x2-2上3個不同的點，求證：當直線PQ與PR都和圓x2+y2=1相切時，直線QR也和該圓相切.

該文得到并證明了：

命題2 過拋物線C1:x2=2py上的點A向⊙C2:x2+(y-b)2=r2(其中p>0，b>0，r>0)引2條切線AB，AC,分別交拋物線C1于點B，C，聯結BC，則直線BC是⊙C的切線的充要條件是2pb=r2+2pr.

該文最后得到了一個猜想,筆者證明之:

證明 設A(acosθ1,bsinθ1)，B(acosθ2,bsinθ2)，C(acosθ3,bsinθ3)，則直線AB的方程為

a(cosθ2-cosθ1)(y-bsinθ1)=b(sinθ2-sinθ1)(x-acosθ1)，

即

因為AB與圓x2+y2=r2相切，所以

即

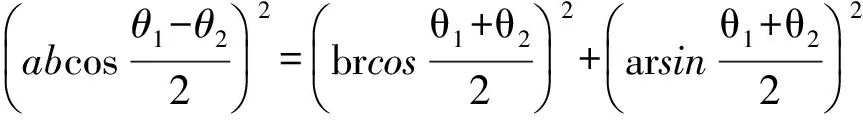
從而

[a2b2+(a2-b2)r2]cosθ1cosθ2+[a2b2-(a2-b2)r2]sinθ1sinθ2+[a2b2-(a2+b2)r2]=0，

(1)同理，由直線AC與x2+y2=r2相切，得

(2)

b2[a2b2+(a2-b2)r2]x1x+a2[a2b2-(a2-b2)r2]y1y+a2b2[a2b2-(a2+b2)r2]=0，

從而直線BC與圓x2+y2=r2相切的充要條件是

(3)

b[a2b2+(a2-b2)r2]=a[a2b2-(a2-b2)r2]，

圖2

1)求圓G的半徑r；

2)過點M(0,1)作⊙G的2條切線交橢圓于點E，F，證明：直線EF與⊙G相切．

(2009年江西省數學高考文科壓軸題)

進一步研究得到:

a2r2(a+m+r)2=b2(a+m+r)2(a+m-r)(a-m-r)，

注意到(a+m+r)2>0，得a2r2=b2[(a-r)2-m2]，整理得

(a2-b2)r2+2ab2r+b2(m2-a2)=0.

(充分性)設A(acosθ1,bsinθ1)，B(acosθ2,bsinθ2)，C(acosθ3,bsinθ3)，即A(x1,y1)，B(x2,y2)，C(x3,y3)，則直線AB的方程為

a(cosθ2-cosθ1)(y-bsinθ1)=b(sinθ2-sinθ1)(x-acosθ1)，

即

因為AB與圓(x-m)2+y2=r2(其中m≥0，r>0)相切，所以

即

亦即

從而b2(m2-r2)[1+cos(θ1+θ2)]-a2r2[1-cos(θ1+θ2)]-2ab2m(cosθ1+cosθ2)+a2b2[1+cos(θ1-θ2)]=0，

即 [b2(m2-r2)+a2(r2+b2)]cosθ1cosθ2+ [a2(-r2+b2)-b2(m2-r2)]sinθ1sinθ2-

2ab2m(cosθ1+cosθ2)+b2(m2-r2)+a2(b2-r2)=0.

因為(a2-b2)r2+2ab2r+b2(m2-a2)=0，所以

ab2(a-r)cosθ1cosθ2+ab2rsinθ1sinθ2-ab2m(cosθ1+cosθ2)+a2(b2-r2)-ab2r=0，

即

b2(a-r)x2cosθ1+abry2sinθ1-b2m(acosθ1+x2)+a2(b2-r2)-ab2r=0.

同理，直線AC與圓(x-m)2+y2=r2(其中m≥0，r>0)相切，得

b2(a-r)x3cosθ1+abry3sinθ1-b2m(acosθ1+x3)+a2(b2-r2)-ab2r=0，

從而點B，C在直線b2(a-r)xcosθ1+abrysinθ1-b2m(acosθ1+x)+a2(b2-r2)-ab2r=0上，此直線方程可以寫成

b2[(a-r)cosθ1-m]x+abrysinθ1+a2(b2-r2)-ab2r-ab2mcosθ1=0.

注意到(a2-b2)r2+2ab2r+b2(m2-a2)=0，得

a2r2+b2m2=[b(r-a)]2， [b(r-a)]2-a2r2=b2m2，

從而圓心C2到直線BC的距離為

圖3

這說明直線BC與⊙C2相切.

有趣的是我們還可以繼續研究一個圓錐曲線的外接多邊形是另一個圓錐曲線內切多邊形的問題(如圖3).

但是要獲得一般結論，初等數學可能無能為力，希望讀者進一步研究.

(本文得到胡曉昊老師的支持，在此一并感謝.)