分布參數雙層隔振系統建模及其振動傳遞特性*

楊明月， 孫玲玲， 王曉樂

(山東大學高效潔凈機械制造教育部重點實驗室 濟南，250061)

?

分布參數雙層隔振系統建模及其振動傳遞特性*

楊明月， 孫玲玲， 王曉樂

(山東大學高效潔凈機械制造教育部重點實驗室 濟南，250061)

從振動能量傳遞觀點及工程實際隔振設計的角度出發，建立了中間連續筏體和中間分散質量兩類雙層隔振系統的解析模型。考慮連續筏體、隔振器及安裝基礎的分布參數特性，基于導納矩陣理論對兩類雙層隔振系統的動態特性傳遞方程進行了理論推導。以功率流為價值函數揭示了系統振動傳遞機理并闡述了實際雙層隔振設計需遵循的一般規律。實例研究表明：力矩激勵在隔振系統能量傳輸中扮演著重要角色，應盡量減少力矩擾動帶來的能量注入；在能耗效率及安裝空間允許條件下，適當放大中間質量可獲得更佳的隔振效果；中間筏體的柔性、隔振器的分布參數特性以及安裝基礎的非剛性因素使得中高頻隔振性能惡化，采用中間分散質量方案可有效避免筏體柔性模態影響，并能顯著降低隔振器駐波同柔性筏體模態間的耦合交互引起的能量峰值。

雙層隔振； 中間質量； 導納矩陣； 分布參數； 駐波效應

引言

在能源日益緊張的當今，為提高能耗利用效率，大量輕薄化結構廣泛應用在車輛、艦船、航空航天器中，加之動力裝置的高速重載化趨勢，使得安裝基礎的柔性特質凸顯，由此激發的基礎結構高頻振動及其輻射噪聲成為亟待解決的工程實際問題。在振動控制措施當中，最常用的是振動隔離技術[1]。高頻域的隔振研究開始較早，Unger等[2]及Snowdon[3]給出了高頻隔振設計應遵循的一般準則，即隔振器的駐波效應、基礎的模態特性均需考慮，并指出為提升高頻隔振效果可采取雙層隔振措施。在隔振器駐波效應研究方面，文獻[4-5]將橡膠隔振器模化為分布參數的均直桿結構，以闡述隔振器的內共振對系統功率流、力傳遞率及輻射聲功率的影響。文獻[6-7]分別將安裝基礎考慮成分布參數的梁、板類結構，探討了單層隔振系統中隔振器駐波效應及基礎柔性對系統傳遞率、功率流特性的影響。

雙層隔振系統的隔振效果主要取決于插入的中間質量大小。在車船等運載工具內，動力裝置連同輔機設備往往通過隔振支承安裝在大型筏體上，受限于機組維度及安裝空間，筏體的柔性特質在中高頻段極易被激發[8]。因而，相較于單層隔振系統，雙層隔振系統中多出的中間質量結構同上、下兩層隔振支承以及安裝基礎結構間的耦合振動機理更加復雜。以往對于雙層隔振系統的理論分析及試驗研究大多采用近似處理方法，主要表現在外擾激勵僅考慮垂向力，忽視力矩激勵成分的影響[9-10]。忽略隔振器的分布參數特性，以復剛度彈簧模型表征其動態特性[11-14]；中間質量考慮成簡單剛體結構[12-14]；安裝基礎認為絕對剛性[9-13]。盡管這些近似處理方法在特定條件下就所研究對象取得了較為滿意的結果，但難以精確闡明高頻域隔振器駐波效應與中間質量的柔性以及安裝基礎彈性模態之間的耦合作用影響機理。鑒于當前雙層隔振系統建模分析的不健全，對雙層隔振系統進行完備的分布參數化建模十分必要。

筆者針對工程實際采用的兩類由多向復合擾動振源(包含力、力矩激勵)、橡膠隔振器、中間質量(柔性連續筏體或分散質量塊)、彈性基礎結構組成的雙層被動隔振系統，建立其分布參數分析模型。基于導納矩陣理論推導總體系統的動態特性傳遞方程。結合實例，以功率流為價值函數探討雙層隔振系統的振動傳遞機理及隔振效果。

1 雙層隔振系統解析模型

從工程實際隔振設計的角度出發，大中型動力機械或發電機組的隔振裝置一般相對坐標平面yOz呈彈性對稱布置。建立圖1 所示的雙層隔振系統解析模型。將其沿結構耦聯界面分為機器A、上層隔振支承B、中間質量C、下層隔振支承D和柔性安裝基礎E五個子系統。中間質量C以其不同的配置形式可劃為兩類[12]：連續筏體結構和分散質量結構。兩類模型中，上層隔振支承包含m個隔振器，下層隔振支承包含n個隔振器。

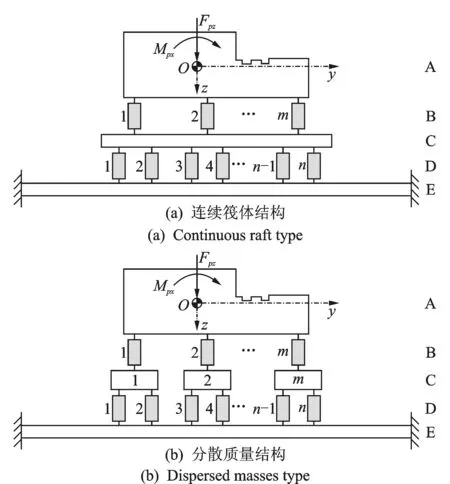
圖1 隔振系統示意圖Fig.1 Scheme of a complete isolation system

為便于分析與綜合，各子系統采用局部坐標系。局部坐標系的建立以及與全局坐標系的轉化關系同文獻[14]。按照振動傳遞方向定義各子系統的輸入輸出端及其廣義擾動力和速度矢量，建立總體系統的耦合振動傳遞模型，如圖2所示。

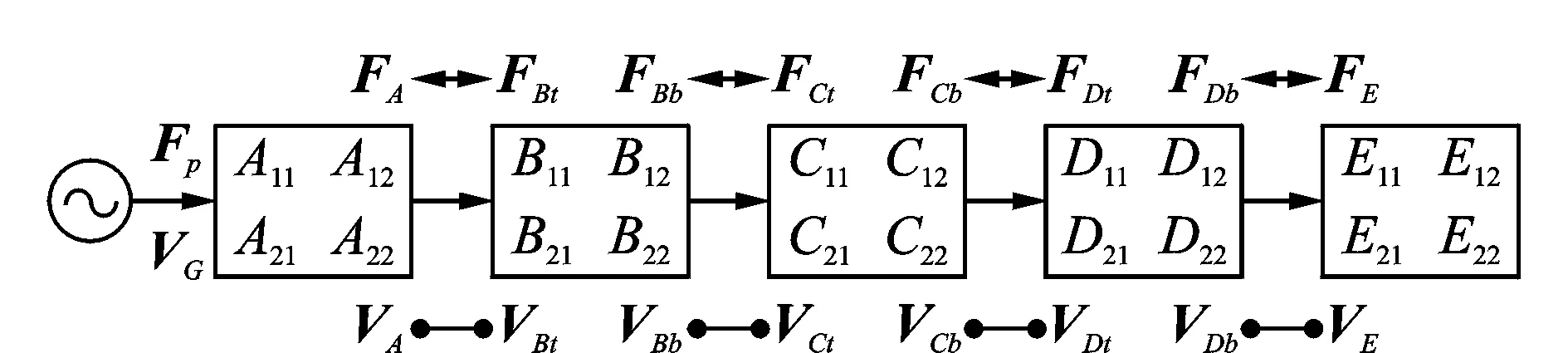
圖2 隔振系統耦合振動傳遞模型Fig.2 Coupled vibration transfer model of isolation system

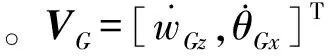
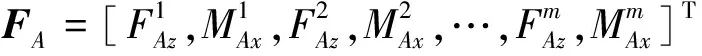
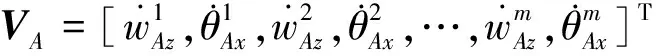
上層隔振支承子系統中m個隔振器輸入、輸出端的廣義力與速度響應矢量分別為

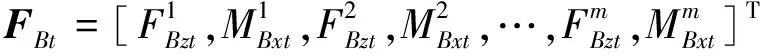
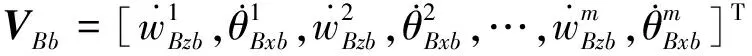
上層隔振支承輸入到中間質量子系統的廣義力及相應速度矢量分別為

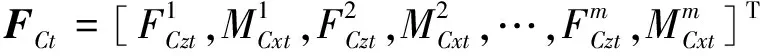
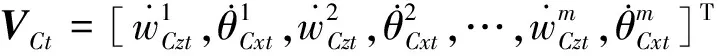
中間質量子系統對下層隔振支承輸出的力與相應的速度矢量分別為

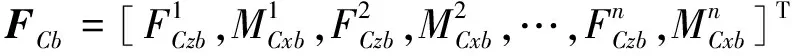
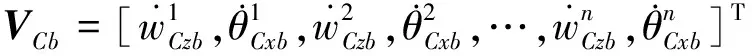
下層隔振支承子系統中n個隔振器輸入、輸出端的廣義力與速度響應矢量分別為

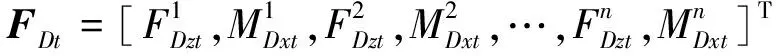
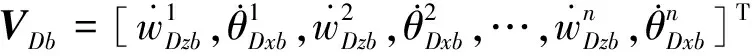
安裝基礎上n個輸入接點處的力與速度矢量分別為

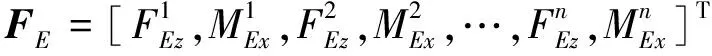
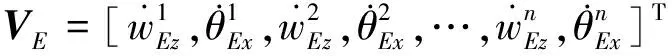
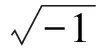
2 子系統分析與綜合

2.1 機器子系統

通常，機器(尤其是大型設備)的基頻遠大于外擾頻率，可視為一般剛性結構。根據牛頓運動定律及結構幾何關系，建立機器子系統在外擾激勵下的動態方程，以導納矩陣形式表述為

(1)

2.2 隔振支承子系統

因黏彈性橡膠隔振器的分布參數特性會在高頻誘發駐波效應，降低隔振效率。傳統的集總參數模型無法準確預估此時的隔振效果，故將其模化為具有分布質量和遲滯阻尼的圓筒形桿。

導納矩陣形式描述的上、下層隔振支承子系統動態特性傳遞方程分別為

(2)

(3)

Mij中元素為兩端同時受力與力矩激勵自由桿的原點導納(i=j)及跨點導納(i≠j)函數，具體表達式詳見文獻[7]。

2.3 基礎子系統

充分考慮安裝基礎的柔性，以兩端固定細長梁模擬基礎子系統E。描述其結構振動特性的導納矩陣方程為

VE=EFE

(4)

其中：導納矩陣E中具體元素為

其中：l為激勵點；k為響應點。

ek,l中各導納元素可采用模態疊加法獲得，具體表達式為

(5)

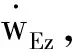
2.4 中間質量子系統

當中間質量子系統為連續筏體時，不能僅視為剛性結構，其柔性特質必須計及，故而模化為兩端自由邊界條件細長梁，以導納矩陣形式描述的整體動態特性方程為

(6)

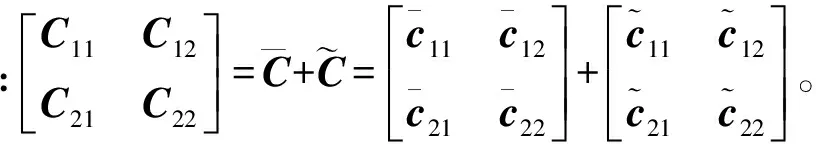
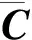
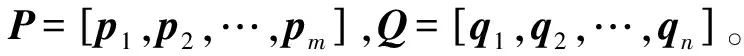
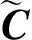
其中：l為激勵點；k為響應點。

(7)

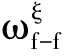
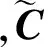
當中間質量子系統為分散質量時，視各分散質量塊為剛體結構。由剛體運動理論，得到第h個分散質量塊的動態特性傳遞方程為

(8)

2.5 子系統動態特性綜合

根據各子系統的動態特性分析, 按照子系統間作用力平衡及速度相等的原則，可推導出整體系統輸入、輸出端的傳遞力與速度響應表達式

VG=[H11-H12(E+H22)-1H21]Fp

(9)

FE=(E+H22)-1H21Fp

(10)

VE=E(E+H22)-1H21Fp

(11)

式(9)～ (11)中，各矩陣具體包含元素為H11=G11-G12(G22+D11)-1G21，H12=G12(G22+D11)-1D12，H22=D22-D21(G22+D11)-1G12，H21=D21(G22+D11)-1G21；G11=F11-F12(F22+C11)-1F21，G12=F12(F22+C11)-1C12，G21=C21(F22+C11)-1F21，G22=C22-C21(F22+C11)-1F12；F11=A11-A12(A22+B11)-1A21，F12=A12(A22+B11)-1B12，F21=B21(A22+B11)-1A21，F22=B22-B21(A22+B11)-1B12。此時，機器復合擾動下輸入到整個系統及通過上、下層隔振支承及中間質量后傳遞到安裝基礎的時間平均功率流可表述為

(12)

其中：上標H表示相應矢量的共軛轉置。

3 系統振動特性分析

根據力與力矩復合激勵下雙層隔振系統動態特性方程的理論推導，以功率流為價值函數，對工程實際中常用的m=2,n=4支承隔振系統進行實例分析。系統主要特征參數見表1所示。

表1中，當αC，βC，αE取0.5時，表示隔振支承相對于中間質量子系統C、安裝基礎子系統E對稱布置。結合隔振設計原則及布局要求，分別取αC=βC=0.5,αE=0.45;κ1=λ1=0.7,κ2=λ2=0.7;ε1=ε3=τ1=τ3=1.25,ε2=ε4=τ2=τ4=0.45。

依據振動基礎理論[15]，計算得到系統中機器的垂向及橫搖振動固有頻率分別為4.13 Hz和14.44 Hz。分布參數隔振器前兩階縱向振動固有頻率為403.11 Hz和806.23 Hz。安裝基礎前七階彎曲振動固有頻率為36.48，101.34，198.63，328.35，490.49，685.07和912.07 Hz。中間連續筏體的橫搖及垂向剛體振動固有頻率分別為6.77 Hz和9.94 Hz，前五階彎曲振動固有頻率為73.68，204.65，401.12，663.08和990.52 Hz。

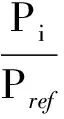
表1 隔振系統主要特征參數

圖3，4為采用中間連續筏體的雙層隔振系統在不同外擾激勵下的功率流頻譜。可以看出，由于系統的橫向穩定性不及垂向，僅傾倒力矩作用對應的功率流幅值在機器橫搖振動剛體模態(14.44Hz)以上頻段內要明顯高于僅垂向力激勵情況，且與復合激勵時的功率流譜幾乎重合。這充分表明了力矩激勵在隔振系統振動能量傳輸過程中起著重要作用，與文獻[7,16]在單層隔振系統中的研究結論一致。因此，無論在理論建模分析以及具體工程實踐中均需考慮力矩擾動成分產生的影響，安裝隔振支承時要確保機器良好的對中性，盡量減少傾倒力矩激勵帶來的能量注入。

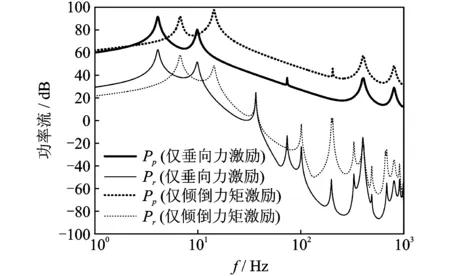
圖3 力/力矩激勵下的系統功率流譜Fig.3 Power flow spectrum under force/moment excitations

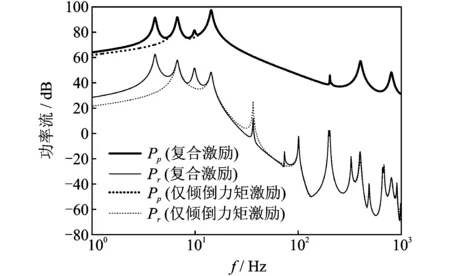
圖4 力矩/復合激勵下的系統功率流譜Fig.4 Power flow spectrum under moment/complex excitations

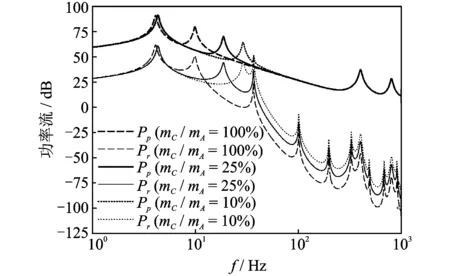
圖5 中間質量大小對系統功率流的影響Fig.5 Influence of different intermediate masses on power flow

為了闡述振動機理、突出分析主要矛盾，以下各圖中外擾激勵均僅施加垂向力。圖5為不考慮中間連續筏體柔性，中間質量mC相對機器質量mA變化時，對系統功率流譜的影響情況。可以看出，隨著質量比逐漸增大，中間筏體對應的垂向剛體振動模態左移，同時使得輸入安裝基礎的功率流幅值下降。這意味著中間質量越大，機器與中間質量的剛體振動模態更加聚攏，且其插入損失越大，系統的隔振效果越好；但過大的中間質量會增加整機負載，給設備安裝布置帶來困難，在實際隔振設計過程中需權衡利弊。

由于大型機器軸向尺寸的縱深及機器艙/室高度方向的制約，中間筏體的維度要與之匹配，使得其柔性特質愈發凸顯。圖6為中間筏體柔性對系統功率流譜的影響。可知，一旦外擾頻率高于中間筏體的彎曲振動基頻(73.68 Hz)，筏體的柔性便明顯反映到輸入基礎的功率流譜中，多出的各階彎曲共振峰(圖中尖箭頭所指，僅出現奇數階模態的原因在于上、下層隔振器均相對中間筏體對稱布置，偶數階模態未被激發)使得中高頻域隔振性能惡化。值得注意的是，中間筏體的第3階彎曲振動模態(401.12Hz)因與隔振器的第1階縱向共振頻率(403.11Hz)接近，誘發強烈的彈性耦合效應，將該階共振峰進一步放大約20 dB，大量振動能注入安裝基礎，導致基礎振動加劇，并極易同空氣介質耦合輻射噪聲。此外，在隔振器的兩階縱向內共振范圍內，安裝基礎的第5階(490.49 Hz)、第6階(685.07 Hz)、第7階(912.07 Hz)彎曲振動模態以及中間筏體的第5階彎曲振動模態(990.52 Hz)亦有不同程度的放大。同時發現，功率流譜中800 Hz左右多出一階波峰(圖中圓箭頭所指)，此附加波峰并非筏體或基礎的共振峰而是因隔振器的第2階縱向內共振(806.23Hz)所引起的能量輸入峰值。

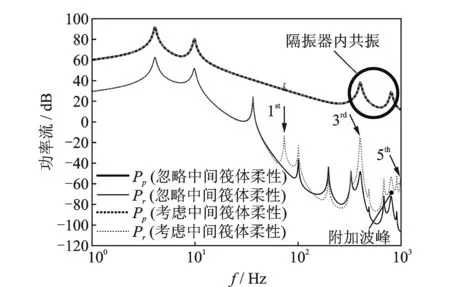
圖6 中間筏體柔性對系統功率流的影響Fig.6 Influence of flexible raft on power flow

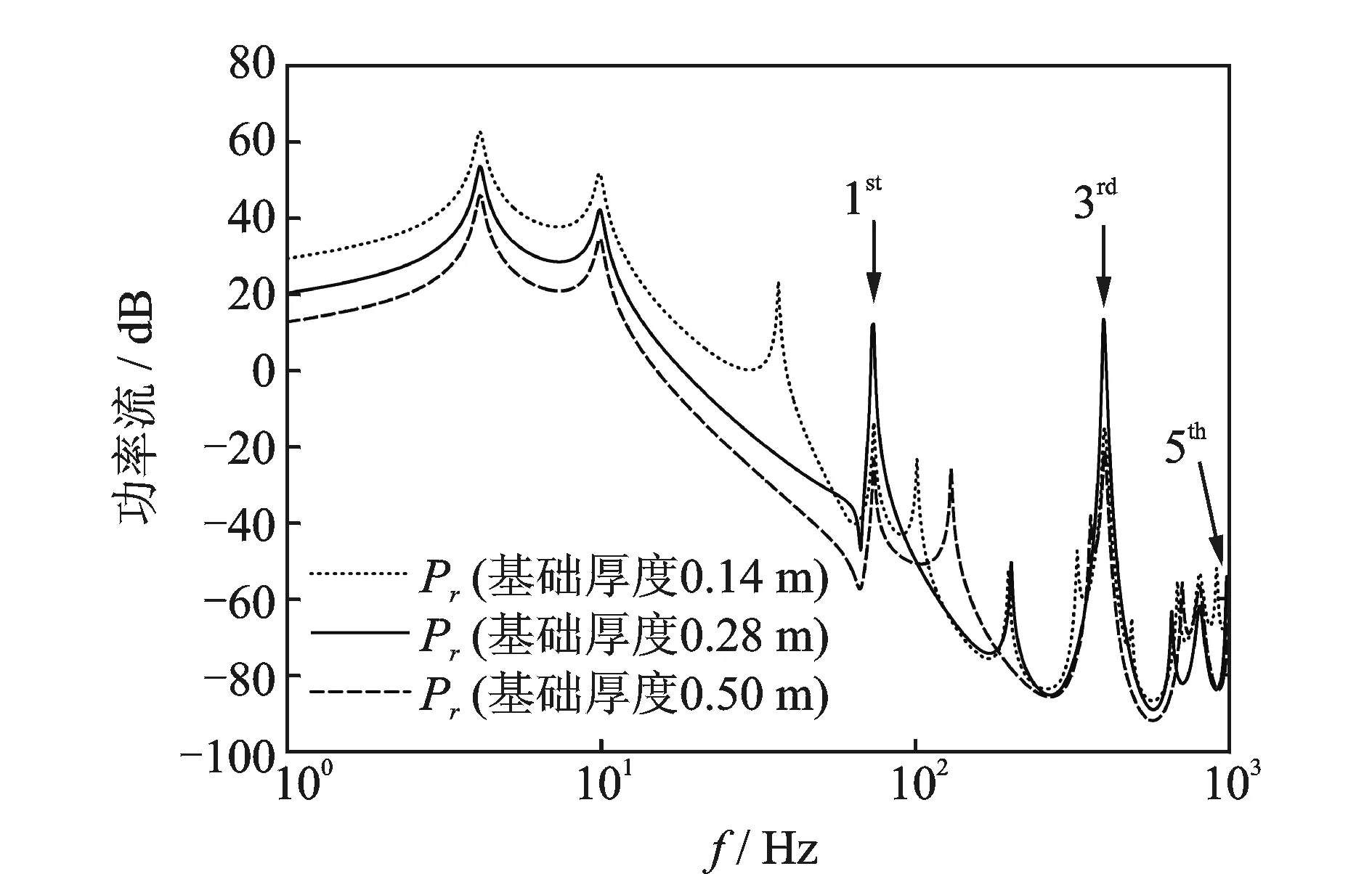
圖7 安裝基礎剛度對系統功率流的影響Fig.7 Influence of foundation stiffness on power flow

圖7為安裝基礎的非剛性在隔振系統能量傳遞過程中產生的影響。需指出的是，工程實際中基礎剛度的改變往往通過增加厚度或加筋處理實現而非改變材料彈性模量。隨著基礎厚度增大，基礎的各階共振峰逐漸移出所關心頻帶，輸入基礎的功率流在全頻段內有所降低，尤其在1～70 Hz內下降明顯。從圖中尖箭頭所指處發現，當基礎厚度為0.28 m時，因其第1階彎曲振動模態(72.97 Hz)與中間筏體的第1階彎曲振動模態(73.68 Hz)相近，誘發強烈的彈性耦合效應，從而放大了該階共振峰。更為嚴重的是，基礎的第3階彎曲振動模態(397.26 Hz)與中間筏體的第3階彎曲振動模態(401.12 Hz)以及隔振器的第1階縱向共振頻率(403.11 Hz)均相近，彈性耦合效應更為強烈，峰值峭立突出，比0.14 m厚時高出近30 dB。因此在隔振設計時，應嚴格避免基礎的彈性模態同中間筏體柔性模態以及隔振器駐波之間的耦合交互現象發生。

上述結論是以往忽略中間連續筏體柔性、安裝基礎的非剛性及隔振器分布參數特性的雙層隔振研究所無法得出的。在隔振設計時，若忽略這些導致隔振效率下降的因素，勢必會高估隔振能力，甚至導致隔振失敗。雙層隔振系統中應用連續的中間筏體有很多優勢，尤其在進行多機組隔振設計時，連續筏體更易保證機組間的同軸度；還可作為半開式的隔聲罩，阻擋機器噪聲向基礎傳播。需注意的是，引入中間筏體后增加的剛體共振峰以及上、下層隔振器駐波和筏體柔性的不利影響。為削弱隔振器的駐波效應，采取的主要措施是安裝同隔振器各階內共振頻率相協調的動力吸振器，此類多層傳遞式動力吸振器的具體實現形式及控制效果詳見文獻[17]。為減小中間連續筏體柔性的影響，可在筏體適當位置敷貼高阻尼材料或者采用含鋼聚合物混凝土結構的中間筏體；在高頻隔振(隔聲)效率要求不高的場合，可采用分散中間質量結構。

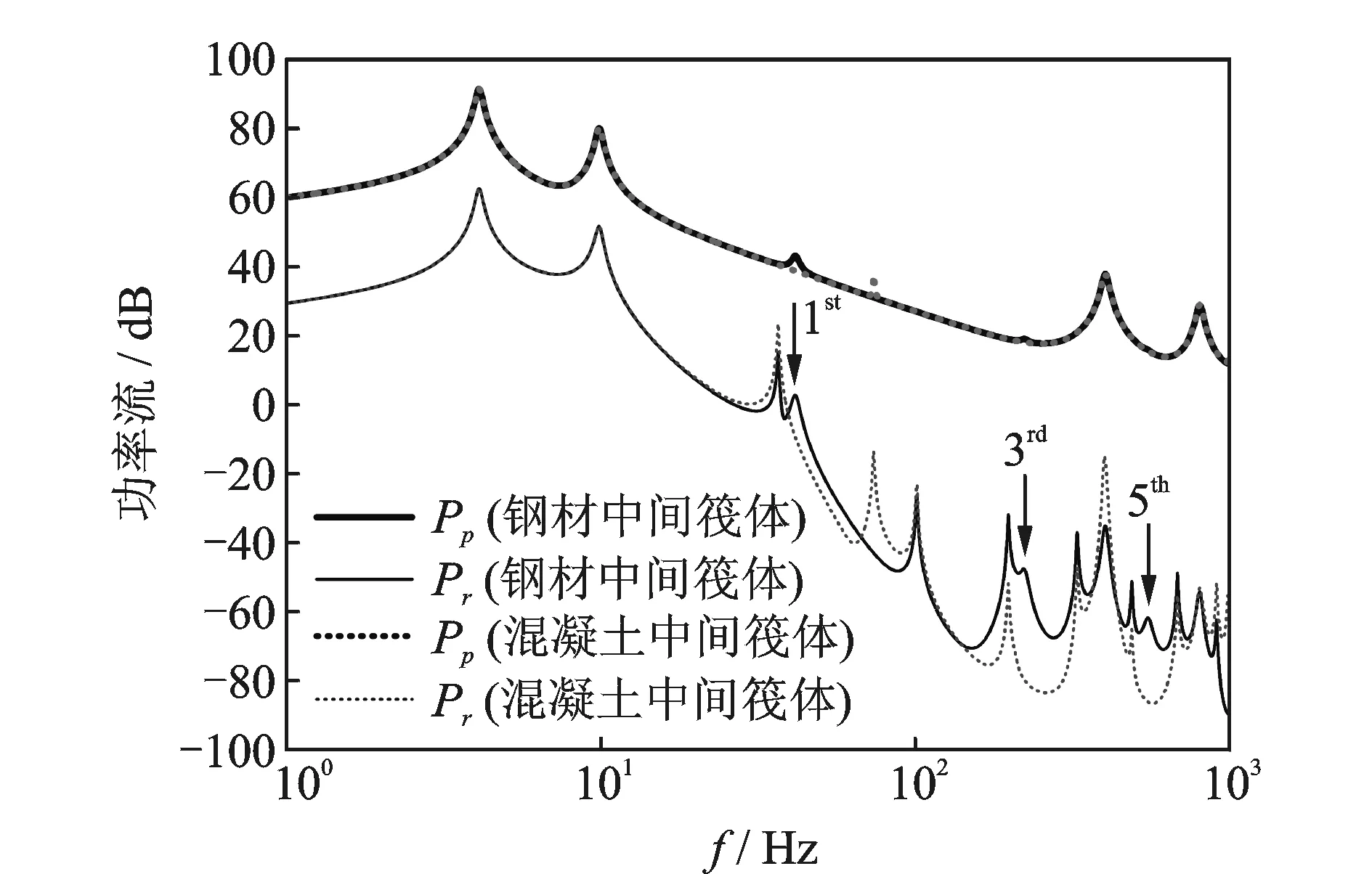
圖8 中間筏體材質對系統功率流的影響Fig.8 Influence of raft material on power flow

若采用含鋼聚合物混凝土結構的中間筏體，依據相關試驗測得數據，取筏體的密度、彈性模量、阻尼損耗因子分別為：ρC=2 800 kg·m-3，EC=2.23×1010N·m-2，ηC=0.06。圖8為兩種材質中間筏體對應的系統功率流頻譜。可見，采用阻尼更大的混凝土中間筏體可明顯削弱筏體彎曲振動各階模態峰值(圖中尖箭頭所指)。由于筏體模態避開了隔振器的各階內共振頻率，所以筏體模態同隔振器駐波的耦合交互也得到了有效抑制。值得注意的是，混凝土筏體的彈性模量通常小于鋼材類筏體一個數量級，這導致了混凝土筏體的彎曲振動模態更容易被激發，在具體隔振設計時筏體的材質及尺寸需進行綜合考量與規劃。

如圖9所示，對比分析圖1兩類雙層隔振系統的振動傳遞特性差異。為便于比較，取分散中間質量塊均等且總質量等于連續筏體質量。可見，采用分散中間質量可有效避免中間連續筏體的柔性模態對中高頻域的影響，對于輸入基礎功率流的削減效果同中間連續筏體方案中僅考慮筏體剛性時相當(對比圖6)；并且能明顯抑制分布參數隔振器及柔性中間筏體模態間的耦合效應，隔振效果優于采用連續筏體方案。此外，分散中間質量系統因無需拆裝整體中間質量，在隔振設備的安裝以及日常維護便捷性方面亦好于連續筏體方案。

4 結 論

1) 力矩激勵在隔振系統能量傳輸中扮演著重要角色，在理論建模分析以及具體工程實踐中均應充分考慮力矩擾動成分產生的影響。

2) 中間質量越大，系統的隔振效果越好，但過大的中間質量會降低能耗效率并受具體設備布置空間限制。中間筏體的材質及尺寸在隔振設計時需進行綜合考量與規劃。

3) 中間連續筏體的柔性、隔振器的分布參數特性以及安裝基礎的非剛性使得中高頻隔振性能惡化，應嚴格限制三者模態間的耦合交互發生。

4) 采用中間分散質量方案可有效避免中間連續筏體柔性模態的影響，并能顯著抑制隔振器駐波同連續筏體柔性模態耦合作用引起的能量輸入峰值。

5)盡管筆者用不同邊界條件的一維桿、梁結構來分別模擬分布參數隔振器、柔性筏體及安裝基礎僅考慮引起結構面外波傳播的激勵組分，但采用的分析方法并不受子系統導納矩陣維度延拓或縮聚的限制，可推廣到板、殼類結構及多層、多振源、面內外波耦合傳播的隔振系統振動特性的研究。對后續的雙層隔振系統靈敏度分析、參數最優化設計、主動控制策略研究以及工程隔振設計實踐具有一定的指導意義。

[1] Rivin E I. Passive vibration isolation[M]. New York：ASME Press, 2003：3-5.

[2] Unger E E, Dietrich C W. High-frequency vibration isolation[J]. Journal of Sound and Vibration, 1966, 4(2)：224-241.

[3] Snowdon J C. Vibration isolation: use and characteri-zation[J]. Journal of the Acoustical Society of Amer-ica,1979, 66(5)：1245-1274.

[4] Kim S, Singh R. Vibration transmission through an isolator modelled by continuous system theory[J]. Journal of Sound Vibration, 2001, 248(5)：925-953.

[5] Du Y, Burdissoa R A, Nikolaidis E, et al. Effects of isolators internal resonances on force transmissibility and radiated noise[J]. Journal of Sound and Vibration, 2003, 268(4)：751-778.

[6] Xiong Yeping, Song Kongjie, Ai Xing. Influence of flexible foundation on isolator wave effects[J]. Shock and Vibration,1996,3(1)：61-67.

[7] Sun L, Leung A Y T, Lee Y Y, et al. Vibrational power-flow analysis of a MIMO system using the transmission matrix approach[J]. Mechanical Systems and Signal Processing, 2007, 21(1)：365-388.

[8] Hansen C H, Snyder S D, Qiu Xiaojun, et al. Active control of noise and vibration, second edition[M]. Boca Raton: CRC Press, 2012：181-185.

[9] 楊鐵軍, 顧仲權, 劉志剛, 等. 雙層隔振系統耦合振動主動控制試驗研究[J]. 振動工程學報, 2003, 16(2)：149-152.

Yang Tiejun, Gu Zhongquan, Liu Zhigang, et al. Experimental research on active control of coupled vibration for a two-stage isolation system[J]. Journal of Vibration Engineering, 2003, 16(2)：149-152. (in Chinese)

[10]段小帥, 梁青, 陳紹青, 等. 雙層隔振系統隔振效果評價與試驗[J].振動、測試與診斷, 2010, 30(6)：694-697.

Duan Xiaoshuai, Liang Qing, Chen Shaoqing, et al. Evaluation and experiment on vibration-isolation effect of double-stage vibration-isolation system[J]. Journal of Vibration，Measurement & Diagnosis, 2010, 30(6)：694-697. (in Chinese)

[11]Xie S, Or S W, Chan H L A, et al. Analysis of vibration power flow from a vibrating machinery to a floating elastic panel[J]. Mechanical Systems and Signal Processing, 2007, 21(1)：389-404.

[12]Moore S. Analytical modelling of single and two-stage vibration isolation systems[C]∥Proceeding of Acoustics 2011. Gold Coast：[s.n.], 2011：1-8.

[13]肖斌, 李彪, 夏春艷, 等. 基于功率流法雙層隔振系統振動傳遞[J]. 機械工程學報,2011,47(5)：106-113.

Xiao Bin, Li Biao, Xia Chunyan, et al. Power flow method used to vibration transmission for two-stage vibration isolation system[J]. Journal of Mechanical Engineering, 2011, 47(5)：106-113. (in Chinese)

[14]史冬巖, 孔令成, 石先杰, 等. 導納理論的隔振系統功率流分析[J]. 哈爾濱工程大學學報,2013,34(6)：748-752.

Shi Dongyan, Kong Lingcheng, Shi Xianjie, et al. Power flow analysis of vibration isolation system with admittance theory[J]. Journal of Harbin Engineering University, 2013, 34(6)：748-752. (in Chinese)

[15]Fahy F J, Gardonio P. Sound and structural vibration: radiation, transmission and response[M]. Oxford：Academic Press, 2007：115-121.

[16]Sanderson M A. Vibration isolation: moments and rotations included[J]. Journal of Sound and Vibration, 1996, 198(2)：171-191.

[17]Dylejko P G, MacGillivray I R. On the concept of a transmission absorber to suppress internal resonance[J]. Journal of Sound and Vibration, 2014, 333(10)：2719-2734.

*國家自然科學基金資助項目(51174126)

2014-04-17；

2014-07-16

10.16450/j.cnki.issn.1004-6801.2015.01.027

TB55; TH138

楊明月，女，1989年4月生，碩士研究生。主要研究方向為振動噪聲分析與控制和現代隔振減振方法。 E-mail：sduyangmy@163.com 通信作者簡介：孫玲玲，女，1967年12月生，博士、教授。主要研究方向為振動理論與應用、結構振動噪聲控制策略。 E-mail：sunll@sdu.edu.cn