用集成過程神經(jīng)網(wǎng)絡預測民航發(fā)動機振動趨勢*

雷 達， 鐘詩勝

(哈爾濱工業(yè)大學機電工程學院 哈爾濱，150001)

?

用集成過程神經(jīng)網(wǎng)絡預測民航發(fā)動機振動趨勢*

雷 達， 鐘詩勝

(哈爾濱工業(yè)大學機電工程學院 哈爾濱，150001)

提出了一種集成過程神經(jīng)網(wǎng)絡預測模型用于民航發(fā)動機振動信號趨勢預測。首先，對AdaBoost.RT算法的誤差函數(shù)進行了改進，并采用自適應調(diào)整策略在訓練過程中自動調(diào)節(jié)算法的分類閾值；然后，以改進的AdaBoost.RT算法為集成學習框架構建集成過程神經(jīng)網(wǎng)絡(process neural network,簡稱PNN)預測模型。通過對兩組實際民航發(fā)動機振動信號序列的預測對集成模型的預測效果進行了評估。結果表明，在具有更加簡單網(wǎng)絡結構的情況下，集成PNN模型的預測效果好于單一PNN模型。此外，提出的改進AdaBoost.RT算法的效果優(yōu)于原始AdaBoost.RT以及僅改進了閾值調(diào)整方法的AdaBoost.RT算法。對比結果表明，提出的集成PNN模型適用于民航發(fā)動機振動信號變化趨勢預測。

航空發(fā)動機； 振動信號； 趨勢預測； 集成學習； AdaBoost.RT； 過程神經(jīng)網(wǎng)絡

引言

對排氣溫度、轉子振動等健康狀態(tài)參數(shù)進行監(jiān)測和趨勢預測是民航發(fā)動機健康狀態(tài)監(jiān)控的重要內(nèi)容。時間序列分析、人工神經(jīng)網(wǎng)絡(artificial neural network,簡稱ANN)[1]和過程神經(jīng)網(wǎng)絡[2]等方法都被用來對民航發(fā)動機健康狀態(tài)參數(shù)變化趨勢進行預測。PNN由于模擬了實際生物神經(jīng)元的時間聚合特性，能夠有效處理實際系統(tǒng)中存在的時間累積效應，具有較好的預測效果[3-4]。

目前，一般通過建立全局模型的方法進行發(fā)動機健康狀態(tài)參數(shù)預測，即采用全部的訓練樣本建立一個單一預測模型進行預測。然而，全局模型可能難以完整描述發(fā)動機健康狀態(tài)參數(shù)時間序列的某些局部特性，且模型結構比較復雜。例如，ANN和PNN等神經(jīng)網(wǎng)絡模型在實際應用中難以確定合適的網(wǎng)絡結構，網(wǎng)絡訓練有可能陷入局部最優(yōu)，導致難以獲得最佳的預測精度。集成學習通過組合一組“弱學習機”，即非最佳預測效果的學習機獲得更高的預測精度。AdaBoost就是一種有效的集成學習算法[5]。AdaBoost賦予上一次學習中錯誤樣本更大的權重，按照權值從訓練樣本中選擇一部分“硬”樣本訓練新的學習機，使得各個學習機適應于當前選擇的局部樣本。通過不同學習機對不同局部樣本的學習，AdaBoost可以克服全局模型的不足，在不追求單個學習機最佳預測精度的同時獲得較好的總體預測效果。可見，采用集成學習模型可以減少模型優(yōu)化的相關工作，容易獲得比單一模型更好的預測效果。

有鑒于此，筆者針對民航發(fā)動機振動信號趨勢預測問題，對面向回歸問題的AdaBoost.RT[6]算法進行了改進，以改進的AdaBoost.RT算法作為集成學習框架，以PNN作為弱學習機構建集成PNN預測模型對民航發(fā)動機振動信號進行趨勢預測。

1 過程神經(jīng)網(wǎng)絡

前饋過程神經(jīng)網(wǎng)絡模型是最為常用的過程神經(jīng)網(wǎng)絡模型，圖1即為一種典型的三層前饋過程神經(jīng)網(wǎng)絡模型。該模型的隱層由過程神經(jīng)元[2]組成，而輸出層由普通神經(jīng)元組成。過程神經(jīng)元以時變函數(shù)作為輸入，以模擬生物神經(jīng)元的持續(xù)輸入刺激，其連接權也為時變函數(shù)，通過積分算子來實現(xiàn)時間聚合運算。

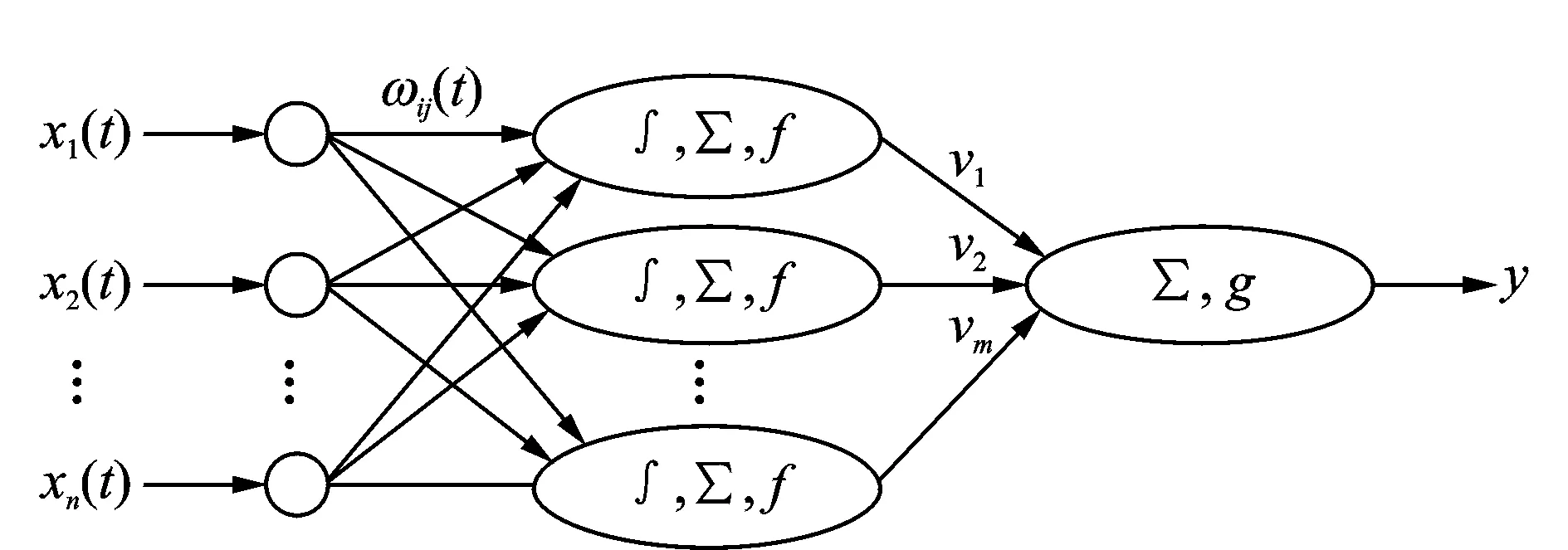
圖1 過程神經(jīng)網(wǎng)絡模型Fig.1 PNN model

假設輸出層的激勵函數(shù)為線性函數(shù)g(z)=z，則圖1所示的過程神經(jīng)網(wǎng)絡模型的系統(tǒng)輸出為

(1)

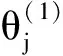
同傳統(tǒng)人工神經(jīng)網(wǎng)絡一樣，過程神經(jīng)網(wǎng)絡可以采用梯度下降法、Levenberg Marquardt算法等進行訓練。同時，為了簡化積分運算，需要將過程神經(jīng)網(wǎng)絡的輸入函數(shù)和權函數(shù)進行正交基展開[7]。

2 集成過程神經(jīng)網(wǎng)絡預測模型

2.1 改進的AdaBoost.RT算法

AdaBoost.RT是從AdaBoost發(fā)展而來的一種面向回歸問題的集成學習算法。AdaBoost.RT計算訓練樣本的相對誤差，引入一個分類閾值φ將回歸問題轉化為分類問題，從而依照AdaBoost框架進行模型訓練。由于其使用的直觀性和簡便性，AdaBoost.RT得到了廣泛的應用[8-9]。因此，筆者采用AdaBoost.RT作為集成過程神經(jīng)網(wǎng)絡模型的基本框架。

由于AdaBoost.RT使用的是相對誤差，因此在實際使用中具有較小值的訓練樣本，在絕對誤差較小的情況下也可能產(chǎn)生較大的相對誤差，導致算法可能集中于具有較小值的樣本，從而失效。為克服上述不足，構造誤差函數(shù)為

(2)

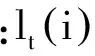
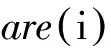
(3)

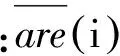
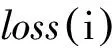
(4)

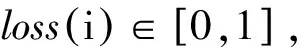
另外，分類閾值φ的大小直接影響AdaBoost.RT的使用效果，過大或者過小的φ都會對算法的預測效果造成影響，導致難以選擇合適的φ[10]。筆者提出一種根據(jù)誤差變化自適應調(diào)整閾值的改進方法。首先，賦予φ一個合適的初始值；然后，讓φ隨著實際訓練誤差的變化而自適應調(diào)整，具體為

(5)

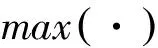
如果訓練誤差變大，則應當增加φ值，反之則減小φ值。另外，為了保證算法的有效性，應當對φ的取值范圍進行限定。當φ值大于訓練誤差lt的最大值或者小于lt的最小值時，筆者取φ為lt的中值。

2.2 集成預測模型構造

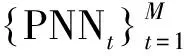
改進的AdaBoost.RT算法步驟如下。

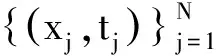
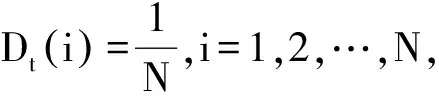
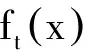
按照下式更新權值Dt

其中：Zt為標準化因子。

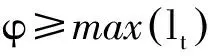
4) 輸出

3 應用實例

3.1 數(shù)據(jù)預處理與模型建立

民航發(fā)動機轉子振動狀態(tài)體現(xiàn)了發(fā)動機的健康狀態(tài)，一般通過與基線的偏差值(百分比)來描述。振動偏差值越大，表明發(fā)動機偏離基線越多，發(fā)動機的性能可能發(fā)生了衰退。因此，有必要對發(fā)動機振動信號的變化趨勢進行預測。

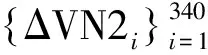
筆者采用平均絕對百分誤差(mean absolute percentage error,簡稱MAPE)以及均方根誤差(root mean square error，簡稱RMSE)描述預測誤差。MAPE和RMSE的計算公式分別為

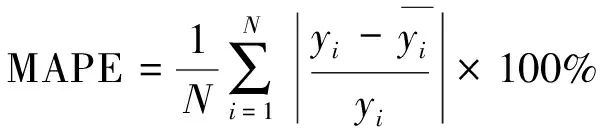
(6)

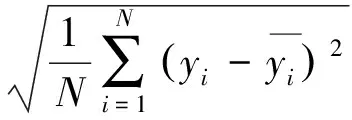
(7)

3.2 測試結果

為了進行對比，在采用本研究方法進行預測的同時采用單一PNN、原始AdaBoost.RT以及文獻[8]的改進AdaBoost.RT算法進行預測。為方便起見，記文獻[8]的改進AdaBoost.RT算法為Ref方法。在實驗中，本研究方法和Ref方法的閾值初始值為φ=0.2，原始AdaBoost.RT的閾值φ通過試探確定。另外，3種集成預測模型的迭代次數(shù)(弱學習機個數(shù))及弱學習機隱層神經(jīng)元個數(shù)通過試探確定。單一PNN的隱層神經(jīng)元個數(shù)通過交叉驗證確定。以上方法均采用選定的相同參數(shù)設置進行5次重復試驗，取平均值作為最終預測結果。

各模型對ΔVN2序列的預測結果如圖2～4所示。模型參數(shù)設置和誤差見表1。各模型對ΔVN1序列的預測結果如圖5～7所示。模型參數(shù)設置和誤差見表2。

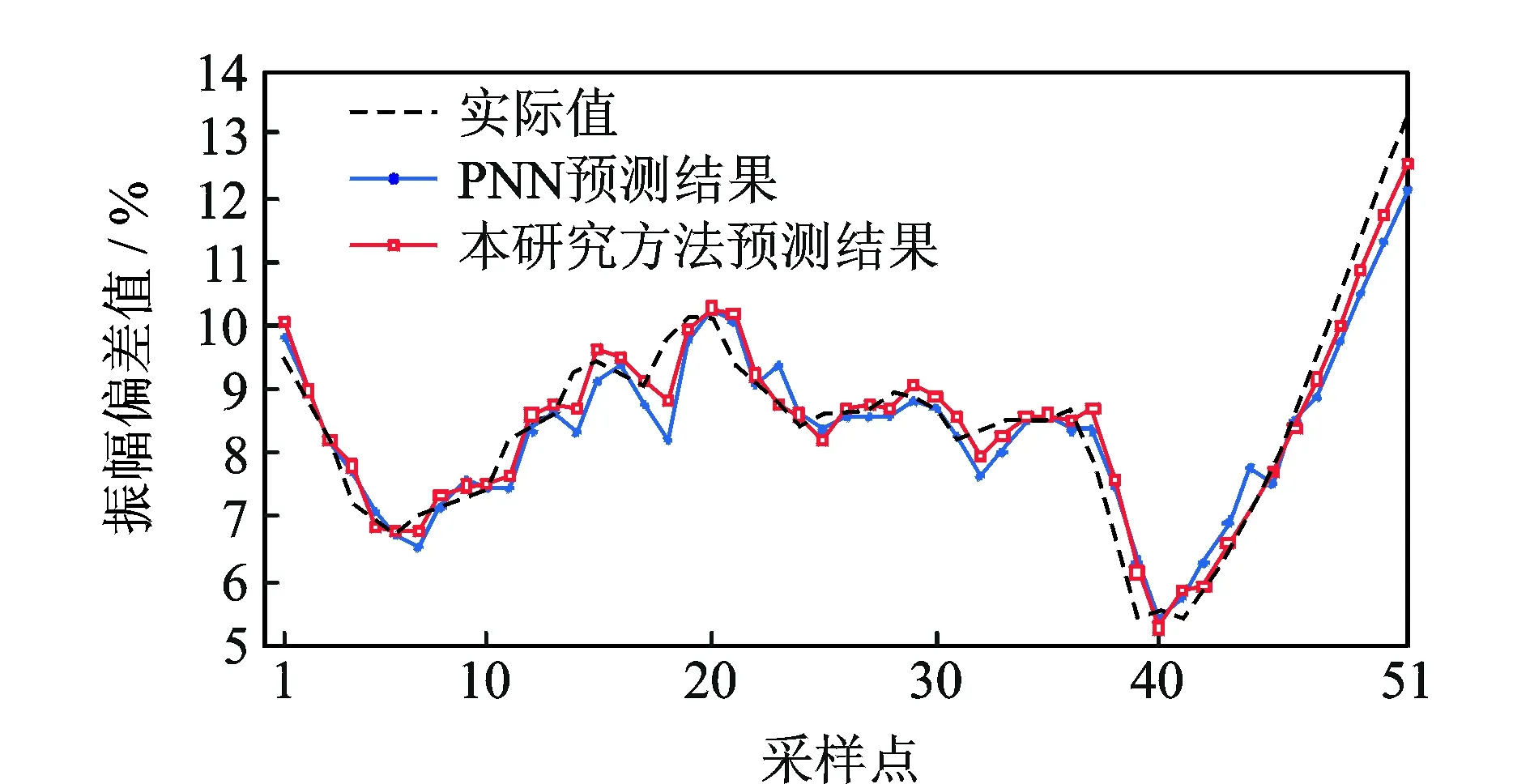
圖2 采用本研究方法的ΔVN2預測結果Fig.2 Prediction results of ΔVN2 using the proposed method

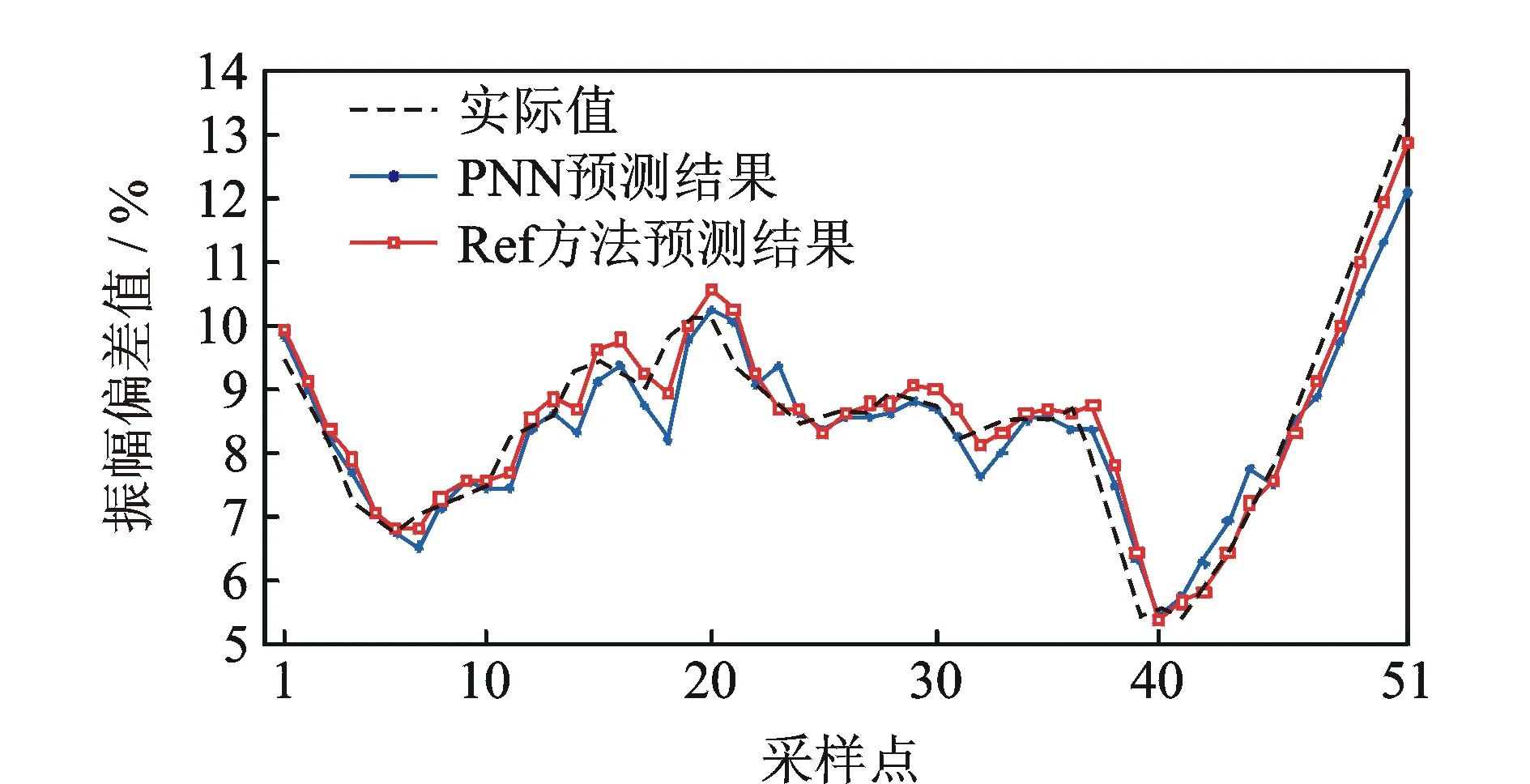
圖3 采用Ref方法的ΔVN2預測結果Fig.3 Prediction results of ΔVN2 using the reference method

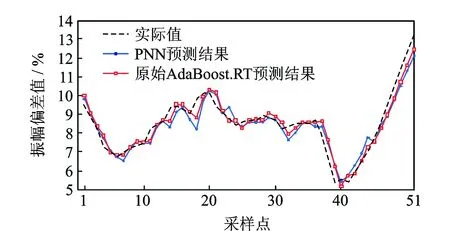
圖4 采用原始AdaBoost.RT方法的ΔVN2預測結果Fig.4 Prediction results of ΔVN2 using the original AdaBoost.RT

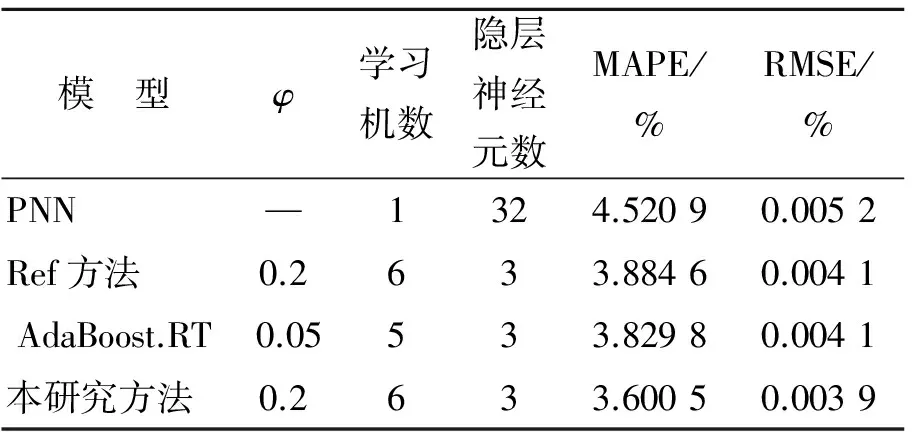
表1 模型參數(shù)設置和ΔVN2預測誤差

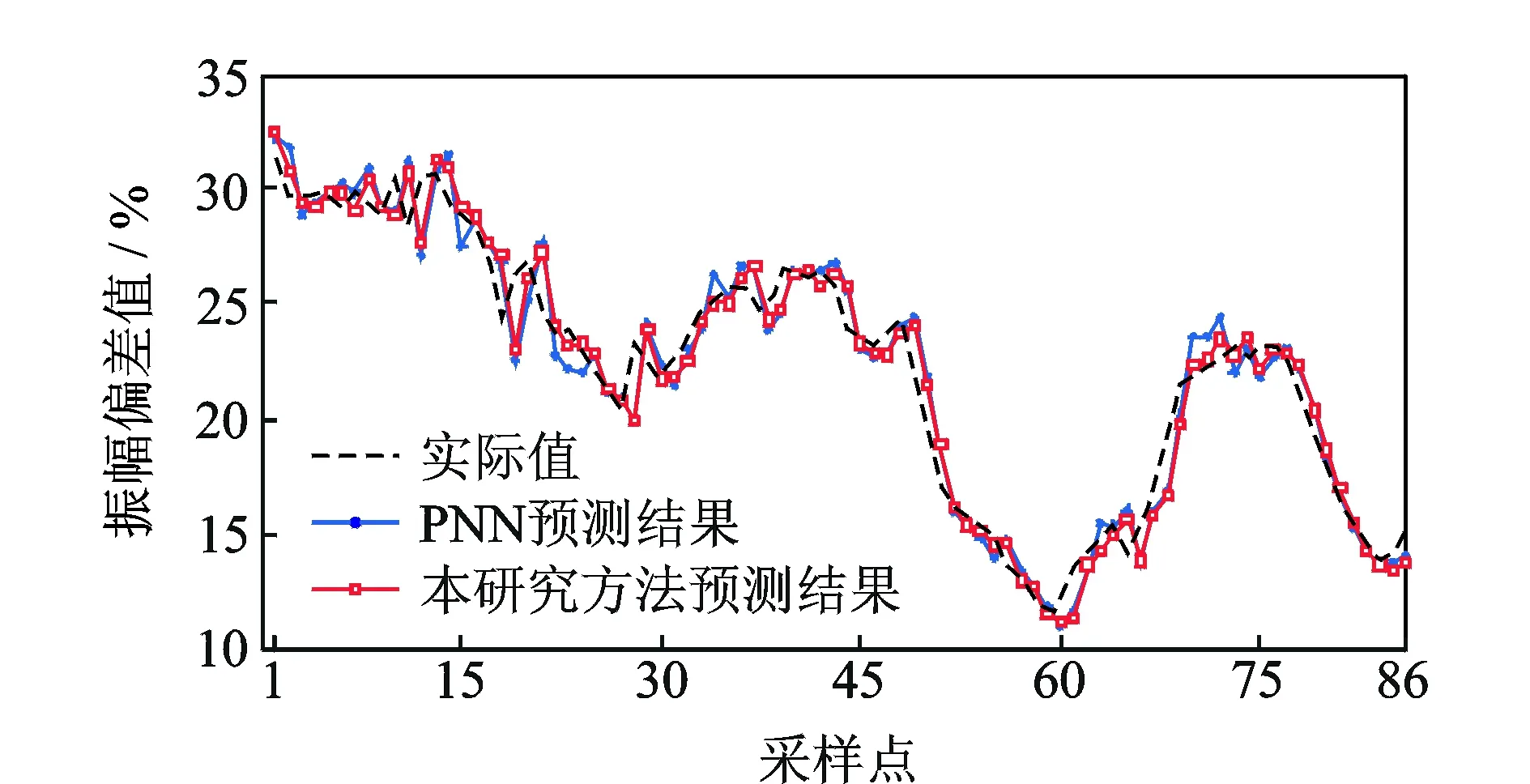
圖5 采用本研究方法的ΔVN1預測結果Fig.5 Prediction results of ΔVN1 using the proposed method

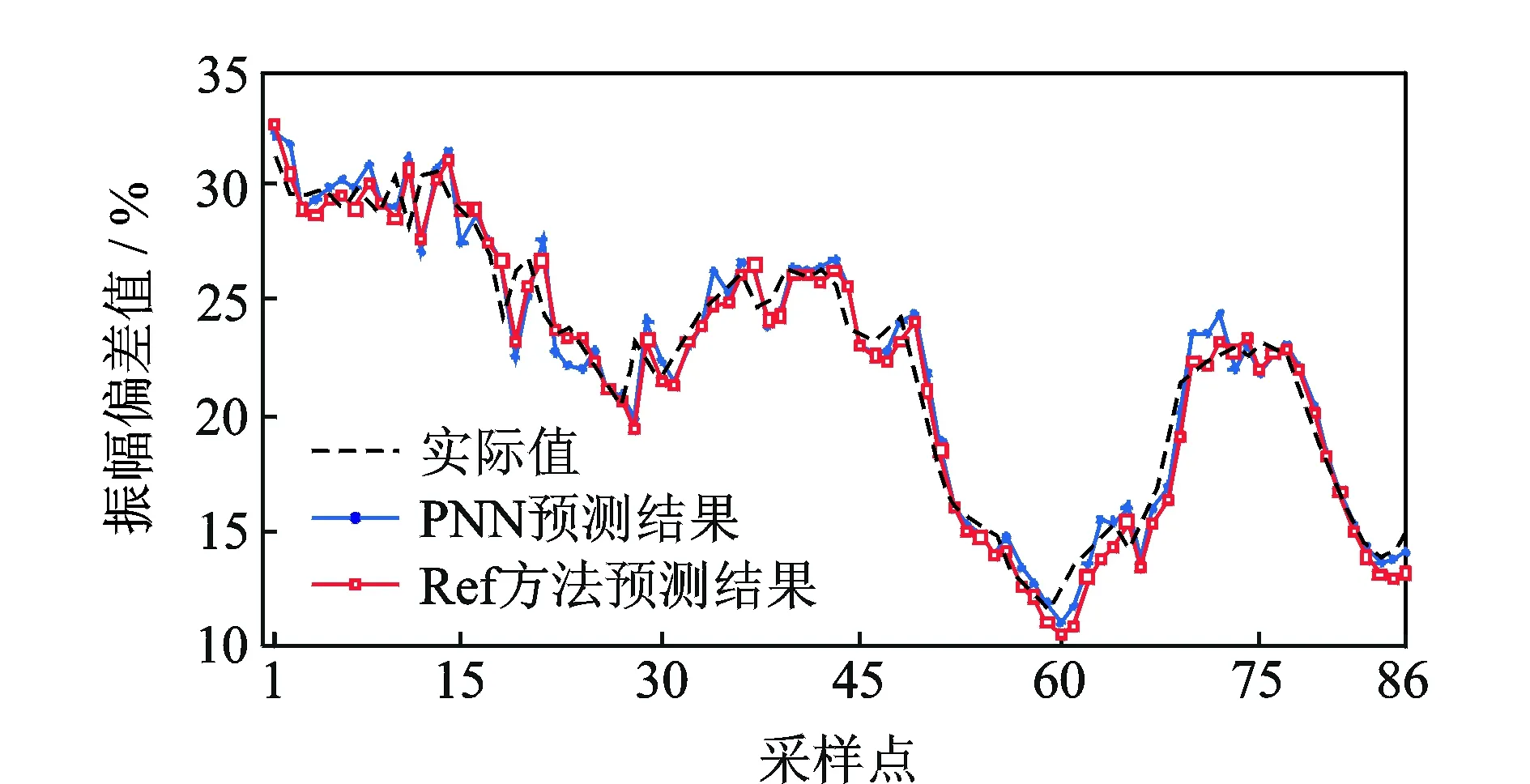
圖6 采用Ref方法的ΔVN1預測結果Fig.6 Prediction results of ΔVN1 using the reference method

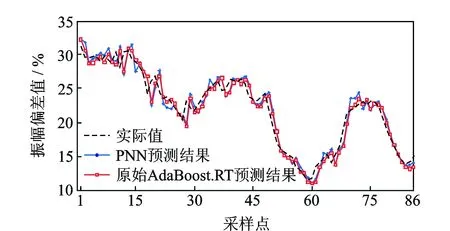
圖7 采用原始AdaBoost.RT方法的ΔVN1預測結果Fig.7 Prediction results of ΔVN1 using the original AdaBoost.RT

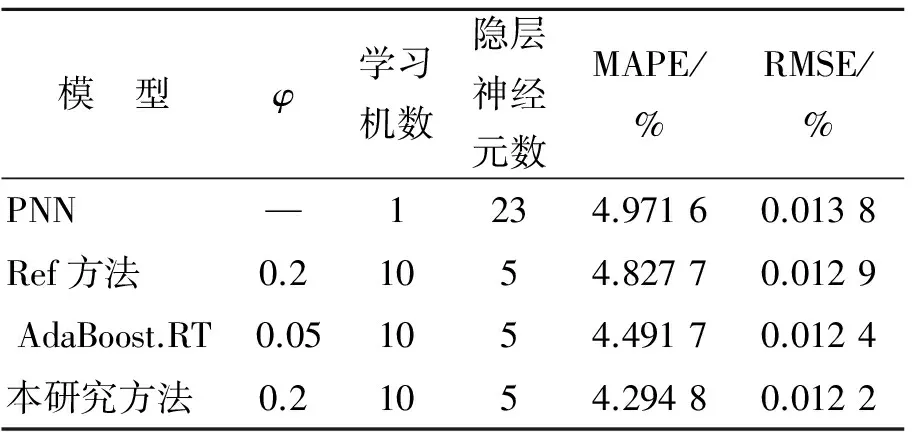
表2 模型參數(shù)設置和ΔVN1預測誤差

可以看出，對于兩種不同類型的振動信號時間序列，在不同訓練樣本和測試樣本比例的條件下，集成PNN預測模型的預測效果都好于單一PNN的預測效果，且作為弱學習機的PNN的網(wǎng)絡結構比單一PNN的網(wǎng)絡結構簡單，證明了通過集成次優(yōu)PNN模型獲得較好預測效果的方法是可行的，從而可以有效簡化民航發(fā)動機健康狀態(tài)預測建模中模型優(yōu)化工作。

雖然文獻[8]改進算法的預測效果實際上比原始AdaBoost.RT的預測效果略差，但該算法只需給定初始閾值，大大減少了閾值優(yōu)化的相關工作，因此其改進是有效的。筆者提出的集成預測模型對于兩種類型振動信號的預測效果好于未改進的AdaBoost.RT算法以及文獻[8]的改進算法。這是因為本研究對AdaBoost.RT算法的改進采用了更加合理的誤差函數(shù)和自適應閾值調(diào)整方法，易取得較好的預測效果。該結果同時也表明了該模型對于實際發(fā)動機振動信號趨勢預測具有良好的適應性。

4 結 論

1) 提出了一種改進的AdaBoost.RT集成學習算法，該方法采用改進的誤差函數(shù)以避免算法在訓練中向具有較小值的樣本集中，保證了算法的有效性。另外，該方法在訓練過程中可以自適應調(diào)整分類閾值，使用更為方便。

2) 以過程神經(jīng)網(wǎng)絡作為弱學習機，采用改進的AdaBoost.RT算法構建集成模型對民航發(fā)動機振動信號變化趨勢進行預測，并且與單一PNN模型、基于原始AdaBoost.RT以及只改進了閾值調(diào)整方法的AdaBoost.RT算法的集成PNN模型進行了對比。結果表明，本研究方法的預測效果好于對比方法，對民航發(fā)動機振動信號變化趨勢預測具有更好的適應性。

[1] 陳果. 用結構自適應神經(jīng)網(wǎng)絡預測航空發(fā)動機性能趨勢[J].航空學報, 2007, 28(3): 535-539.

Chen Guo. Forecasting engine performance trend by using structure self-adaptive neural network[J]. Acta Aeronautica Et Astronautica Sinica, 2007, 28(3): 535-539. (in Chinese)

[2] 何新貴,梁久禎.過程神經(jīng)網(wǎng)絡的若干理論問題[J].中國工程科學, 2000, 2(12): 40-44.

He Xingui, Liang Jiuzhen. Some theoretical issues on procedure neural networks[J]. Engineering Science, 2000, 2(12): 40-44. (in Chinese)

[3] 金向陽, 林琳, 鐘詩勝, 等. 航空發(fā)動機振動趨勢預測的過程神經(jīng)網(wǎng)絡法[J]. 振動、測試與診斷, 2011,31(3):331-334.

Jin Xiangyang, Lin Lin, Zhong Shisheng, et al. Prediction of aeroengine vibration trend using process neural network[J]. Journal of Vibration, Measurement & Diagnosis, 2011, 31(3):331-334. (in Chinese)

[4] Ding Gang, Zhong Shisheng. Approximation capability analysis of parallel process neural network with application to aircraft engine health condition monitoring [J]. Lecture Notes in Computer Science, 2007, 4493(3): 66-72.

[5] Freund Y, Schapire R. A desicion-theoretic generalization of on-line learning and an application to boosting computational learning theory[J]. Lecture Notes in Computer Science, 1995, 904:23-37.

[6] Solomatine D P, Shrestha D L. AdaBoost.RT: a boosting algorithm for regression problems[J]. Neural Networks, 2004, 2: 1163-1168.

[7] 何新貴,梁久禎,許少華. 過程神經(jīng)網(wǎng)絡的訓練及其應用[J].中國工程科學,2001,3(4):31-35.

He Xingui, Liang Jiuzhen, Xu Shaohua. Learning and applications of procedure neural networks[J]. Engineering Science, 2001, 3(4):31-35.(in Chinese)

[8] Tian Huixin, Mao Zhizhong. An ensemble elm based on modified AdaBoost.RT algorithm for predicting the temperature of molten steel in ladle furnace[J]. IEEE Transactions on Automation Science and Engineering, 2010, 7(1):73-80.

[9] Schclar A, Tsikinovsky A, Rokach L, et al. Ensemble methods for improving the performance of neighborhood-based collaborative filtering[C]∥Proceedings of the Third ACM Conference on Recommender Systems. New York: [s.n.], 2009.

[10]Shrestha D L, Solomatine D P. Experiments with AdaBoost.RT, an improved boosting scheme for regression[J]. Neural Computation, 2006, 18(7): 1678-1710.

[11]Schafer R W. What is a savitzky-golay filter[J]. Signal Processing Magazine, IEEE, 2011, 28(4): 111-117.

*國家高技術研究發(fā)展計劃(“八六三”計劃)資助項目(2012AA040911-1)；國家自然科學基金資助項目(60939003)

2013-01-21；

2013-05-02

10.16450/j.cnki.issn.1004-6801.2015.01.023

TH183； TH263.6

雷達，男，1984年11月生，博士研究生。主要研究方向為復雜裝備健康狀態(tài)監(jiān)測與預測方法。曾發(fā)表《卷積和離散過程神經(jīng)網(wǎng)絡及其在航空發(fā)動機排氣溫度預測中的應用》(《航空學報》2012年第33卷第3期)等論文。 E-mail:leidame@163.com