一種基于可變網格劃分的離群點檢測算法

馬菲，朱昌杰*，鄭穎，鄧杰

(1.淮北師范大學計算機科學與技術學院，安徽淮北 235000;2.江南大學物聯網工程學院，江蘇無錫 214122)

一種基于可變網格劃分的離群點檢測算法

馬菲1，朱昌杰*1，鄭穎1，鄧杰2

(1.淮北師范大學計算機科學與技術學院，安徽淮北 235000;2.江南大學物聯網工程學院，江蘇無錫 214122)

LOF(Local Outlier Factor)算法是常用的離群點檢測算法，但是該算法在面對大規模數據集時往往需要高昂的時空開銷，基于固定網格的離群點檢測算法雖然在一定程度上可以解決該問題，但是它的執行效果易受到網格劃分粒度的影響。對此提出一種基于可變網格劃分的離群點檢測算法。該算法首先根據數據點在空間的實際分布情況來動態構建與原始數據集分布大體一致的網格空間，然后刪除網格中數據點數目超過設定閾值的網格中所有數據點，最后在剩余的數據點集上執行LOF算法。實驗結果顯示，相對于固定網格的離群點檢測算法，所提算法的執行效率明顯提高并且檢測精確度亦有所提高。

局部離群因子;離群點檢測;可變網格;大規模數據集

隨著越來越多的數據被收集并存儲到數據庫中，有效和高效地分析并挖掘包含在這些大規模數據集中的信息具有重要意義［1］。在大規模數據集包含的信息中，由于離群點常常包含潛在有用的信息，對其檢測越來越受到人們的重視。離群點一般被定義為數據集中與其他數據對象差異較大的那些數據對象。離群點檢測目的是發現數據集中的離群點并根據這些離群點推斷潛在的、有價值的知識。隨著大數據時代的到來，離群點檢測在實際生活中得到了廣泛的應用，如在金融領域用來檢測信用卡的異常使用、在工業控制系統中對數據的預處理、網絡監管系統中網絡異常識別、網絡健壯性分析、在醫療領域的公共健康分析、圖形圖像的處理等［2-4］。

LOF(Local Outlier Factor)算法于2000年被Breunig等［5］人提出，它是一個基于密度的算法。LOF算法通過計算數據點的局部離群因子來表征該數據點的偏離程度，使得對離群點的檢測不再是二元結果。LOF算法在進行局部離群因子計算時，檢測精確度常常受到用戶給定參數的影響［6］。同時，在進行大規模數據集中的離群點檢測時，該算法往往需要高昂的時空開銷。

為了解決這些問題，薛安榮等人［7］提出一種改進的局部離群點檢測算法。首先將對象屬性分為固有屬性和環境屬性，然后通過環境屬性確定鄰域對象、固有屬性計算離群因子的方法，有效地避免了參數的輸入，但是該算法對鄰域的確定仍然需要消耗大量的時間。Zhang Ke等人［8］提出一種新的計算局部離群因子算法，與LOF算法相比，該算法時間效率有所提高并且對參數的敏感度也有所降低。Rajendra Pamula等人［9］提出一種基于聚類的離群點檢測算法，該算法首先使用K-means方法進行聚類，然后刪除離聚類中心較近的數據點，最后對剩余的數據點計算局部離群因子。由于該算法刪除了部分的數據點，算法的執行效率相應地得到提高，但是在聚類時使用K-means方法進行聚類，導致算法對初始聚類中心較為敏感。文獻［10］中提出基于網格技術的高維大數據集離群點挖掘算法(Outlier Mining Algorithm based on Grid Techniques，OMAGT)，該算法將網格思想引入其中，把空間劃分為大小相同的網格單元，從而將對數據集中數據點處理轉化為對空間中有限網格單元的處理。通過這種方式能有效地提高算法的執行效率，但是由于該算法使用的是固定網格劃分，所以易受網格劃分粒度的影響，并且它并沒有考慮數據集中數據點的實際分布，這會導致計算結果有一定的偏差。

鑒于此，文中在LOF算法與OMAGT算法基礎上，提出一種基于可變網格劃分的離群點檢測算法(Outlier Detecting Algorithm based on Variab le Grid，ODAVG)。

ODAVG算法首先根據數據集在空間的實際分布情況，將每一維非等寬地劃分成數段，進而在空間中形成大小不一的網格單元;然后統計每個網格單元中數據點的數目，刪除網格中數據點數目大于設定閾值網格中的所有數據點;最后對剩余的數據點利用LOF算法進行離群點檢測。在多個數據集的實驗結果表明，相對于OMAGT算法，ODAVG算法執行效率明顯提高并且準確率也有所提高。

1 LOF算法

1.1 LOF算法的基本概念

在離群點檢測領域，LOF算法常常被用來計算數據點的離群程度，它不再簡單地判別數據點是不是離群點，而是給出數據點的離群程度，實際上反應了該數據點是否偏離相對集中的區域。下面介紹LOF算法的一些基本概念。

定義1(對象p的k距離)

在數據集D中，對于任何一個正整數k，以k-distance(p)來表示對象p的k距離，以d(p，0)表示對象p到對象o(o∈D)的距離。滿足下面兩個條件，則k-distance(p)=d(p，o):

(1)至少有k個對象o'∈D{p}，它到p的距離d(p，o')≤d(p，o);

(2)至多有k－1個對象o'∈D{p}，它到p的距離d(p，o')＜d(p，o)。

定義2(對象p的k-distance鄰域)

已知對象p的k-distance(p)，p的k距離鄰域是指D中的對象q到p的距離不大于k-distance(p)的所有對象的集合，記為

定義3(對象p到對象o的可達距離)

設k是一個自然數，對象p到對象o的可達距離定義為

從可達距離定義可以看出，如果p遠離o，則它們的可達距離等于兩者之間的實際距離;如果p‘足夠地’地接近o，則它們的可達距離等于o的k-distance(o)。

定義4(對象p的局部可達密度)

對象p的局部可達密度定義為

可以看出，p的局部可達密度是p的MinPts個最近鄰居的平均可達距離的倒數。

定義5(對象p的局部離群因子)對象p的局部離群因子定義為

已知，p的局部離群因子顯示p的離群程度。它等于p的MinPts個最近鄰居的局部可達密度的平均值與p的局部可達密度之比。根據公式可以很清楚地看到，p的局部可達密度越小且MinPts個最近鄰居的局部可達密度越大，則離群因子越大，也就是說p越偏離MinPts個鄰居。

1.2 LOF算法的執行步驟

輸入:數據集D，離群點數目n;輸出:前n個局部離群因子值較大的數據對象。1)對于數據對象p，根據公式(1)～(4)來計算該數據對象的局部離群因子;

2)循環遍歷數據集D的每一個對象，重復第一步，并將該結果依次存放到集合Col_LOF中;

3)對Col_LOF中的值用快速排序算法排序，并輸出前n個局部離群因子值較大的數據對象。

2 基于可變網格劃分的離群點檢測

2.1 固定網格劃分

固定網格劃分是基于網格劃分的離群點檢測中常用的一種方法，常與基于密度的離群點檢測算法結合，可以提高算法的執行效率［11］。固定網格劃分，簡單地說，就是將目標數據集每一維進行等間距劃分，而后在空間中形成大小相同的網格單元。設D是一個d維的數據集，其屬性(A1，A2，…，Ad)的取值在一個封閉的區間里。令第i維的取值范圍是［li，hi］，其中i={1，2，…，d}，則

是一個d維的數據空間。取數據集的每一維，將該維等間距地劃分為k段，則d維空間被劃分為kd個網格。第i維的第j個區間段的長度θi=(hi－li)/k，并且該區間段的取值范圍是Iij=(li+(j－1)×θi，li+j×θi)，其中j={1，2，…，k}。

2.2 一種新的可變網格劃分策略

固定網格劃分較易理解并且方便實現，但是如果在高維數據集中使用固定網格劃分的方法，隨著維度的增加，網格的數量以指數級在增長，導致算法的復雜度大大增加，其可用性也因此而降低［12-13］。近年來，不少研究人員展開了關于可變網格劃分技術的研究，如文獻［14］提出的可變網格劃分方法，該方法首先對每一維進行等深度地劃分，然后合并相似度較大的相鄰網格。文獻［15］進行可變網格劃分時引入了屬性維半徑向量這一概念。QIAN Xuezhong等人［16］提出根據數據集的實際分布動態構建網格空間的策略等。

文中介紹一種新的可變網格劃分方法。對于數據集的每一維，首先對其等間距劃分;其次統計該維每個區間中數據點數目并計算相鄰區間段的相似性;最后比較相鄰區間的相似性，對于相似度較高的區間段進行合并。在最后形成的網格空間中，由于每一維數據分布不盡相同，從而進行合并的區間段也不盡相同，所以最后在數據空間中就構成了大小不同的網格。

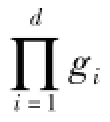
可變網格劃分的執行步驟如下所述:

1)對于第i維，采用固定網格劃分方法對其進行劃分。

2)統計該維每個區間段的數據點數目并計算相鄰段的相似性。由于每個區間段的長度是一樣的，所以采用區間段中數據點的數目Countij來表示其密度，并引入參數來量化相鄰區間段的相似性，其計算方式如下:

3)對于第i維，依次比較相鄰段的相似性是否大于閾值T(0≤T≤1)，其中T用于表示兩個區間段的相似性。如果大于T，則記錄相應的段，否則不做任何操作。比較結束后，對記錄的段進行合并。在實際操作中，如果T值接近1，則表示進行合并的段較少，最終剩余網格的數目較多，算法的執行效率相對較低，但可以保證離群點檢測的精確度;如果T值接近0，表示進行合并的段較多，則最終剩余的網格數目較少，雖然可以提高算法的執行效率，但是會影響離群點檢測的精確度。

4)對每一維均執行1)到3)。

2.3 基于可變網格劃分的離群點檢測算法

通過2.2節提出的可變網格劃分策略，可以對給定的數據集動態地進行網格劃分。劃分后的網格可以盡可能地將相似度大的數據點劃分到同一個網格，相似度小的數據點劃分到不同的網格。文中將上述網格劃分方法與LOF算法相結合，提出基于可變網格劃分的離群點檢測算法。在此引入密度閾值Min P，表示網格中數據點數目。當網格中數據點數目大于Min P時，則認為該網格中數據點是密集的，否則認為是稀疏的。該算法的具體步驟如下:

輸入:數據集D，離群點數目n，密度閾值Min P;

輸出:前n個LOF值較大的數據點。

1)掃描數據集D，采用2.2節所述可變網格劃分方法對空間進行劃分，將劃分后的網格總數記為|grid_counts|。

2)統計網格中數據點的數目Nm，m={1，2，…，|grid_counts|}，并比較Nm是否大于密度閾值M in P，如果大于，則刪除這個網格中的所有數據點，否則不做任何操作。

3)對于剩余的數據點執行LOF算法，并輸出前n個LOF值較大的數據點。

3 實驗與分析

為了測試ODAVG算法的有效可行性，在實驗環境為Matlab R2014a、操作系統W in7(CPU 3.4 Hz，內存:4.00 GB)的平臺上分別從網格劃分效果、執行時間和檢測精確度3個方面對ODAVG算法、OMAGT算法和LOF算法進行對比分析。

3.1 實驗數據集信息

選擇5組數據集對提出算法的有效性進行實驗，其中2組人工數據集Dataset1和Dataset2，3組 UCI標準數據集Shuttle、Breast和KDD Cup。對于人工數據集，采用Matlab R2014a提供的函數mvnrnd(MU，COV，M)進行生成，其中MU為均值，COV為均值對應的協方差，M表示生成數據的規模。Dataset1數據集有3種類型的離群點，共100條。Dataset2數據集有4種類型的離群點，共1 000條。Shuttle數據集共有7個類簇，其中第2類、第6類和第7類相對較少，共54條數據，視此3類為離群點。對Breast數據集中進行處理:把Malignant類減少到83條并視其為離群點。KDD Cup數據集是網絡入侵檢測數據集。5組數據集的基本信息如表1所示。

表1 各個數據集的基本信息Tab.1 Basic in formation of each dataset

3.2 網格劃分效果對比

在進行網格劃分效果對比時，采用Dataset1和Dataset2為測試集，對比OMAGT和ODAVG 2種算法進行網格劃分以及刪除密集數據點后的效果圖并進行分析。為了算法的客觀性，ODAVG算法進行網格劃分時，每一維的初始區間段個數與OMAGT算法進行網格劃分時保持一致。網格劃分的效果如圖1所示。

圖1 2種算法所畫網格效果Fig.1 Grid d ivision result using the tw o algorithm s

從圖1(a)～(d)可以看出:(1)ODAVG算法進行網格劃分后的網格數目要明顯小于OMAGT算法進行網格劃分的數目，這樣可以在后續的處理中提高算法的執行效率;(2)ODAVG算法劃分的網格空間也更加合理，畫出的網格單元更符合數據點的實際分布，這是由于在進行網格劃分時，對相似度較高的相鄰段執行了合并操作。

刪除密集區域后對應的效果如圖2(a)～(d)所示，其中圖1(a)與圖1(b)是二維數據對比結果，圖1(c)與圖1(d)是三維數據對比結果。

圖2 兩種算法刪除密集區域后Fig.2 Delete dense regions using the tw o algorithm s

當密度閾值Min P一定時，從圖2(a)～(d)可以看出，ODAVG算法刪除密集區域后剩余的數據點的數目要小于OMAGT算法剩余的數據點數目，這樣減少了參與LOF算法的數據點數目，提高了ODAVG算法的執行效率。

3.3 執行時間對比分析

首先，以Dataset1作為測試集，從Dataset1中抽取數據量不同的數據集對ODAVG算法、OMAGT算法和LOF算法進行執行時間對比。為了使以上3種算法更具有客觀性，分別執行上述3種算法5遍，選取平均執行時間，并且在網格劃分時，ODAVG算法的每一維初始區間段個數與OMAGT算法進行網格劃分時保持一致。表2表示的是在Min P=400的情況下，選擇不同數據量在ODAVG算法、OMAGT算法和LOF算法的運行時間。

從表2可以看出，ODAVG算法和OMAGT算法的執行時間明顯要低于LOF算法的執行時間，這是因為ODAVG算法和OMAGT算法刪除了大部分參與局部離群因子計算的數據點。由于ODAVG算法是根據數據集的分布將空間劃分大小不同的網格，它并不需要搜尋聚類區域，而OMAGT算法將空間進行網格劃分后，需要搜尋聚類區域，同時與OMAGT算法相比，ODAVG算法刪除較多的數據點，所以ODAVG算法的執行時間低于OMAGT算法的執行時間。

表2 不同數據量的執行時間Tab.2 Execution tim e of the differen t data size

其次，將Dataset2作為測試集，測試在數據量保持不變的情況下，通過改變密度閾值Min P的大小，來對比ODAVG算法、OMAGT算法和LOF算法的執行時間，其中密度閾值的選取分別為300，500，700，900，1 100。為了執行結果的客觀性，每個算法同樣運行5遍，然后取平均值，并且在網格劃分時，ODAVG算法的每一維的初始區間段個數與OMAGT算法進行網格劃分時保持一致。由于LOF算法沒有密度閾值，所以該算法選取執行5遍的時間平均值。表3表示不同密度閾值下3種算法的執行時間。

表3 不同密度閾值下的運行時間Tab.3 Execution time of the different density threshold

從表3可以看出，LOF算法的執行時間明顯高于ODAVG算法和OMAGT算法。當選取不同的密度閾值時，ODAVG算法隨著密度閾值增加，它的執行時間也不斷增加，這是因為當選取的密度閾值增大時，執行刪除操作后剩余的數據點相對較多，因此執行過程消耗的時間相對較多。隨著密度閾值的增大，雖然ODAVG算法的執行時間也在增加，但是增加的幅度并沒有OMAGT算法增加的幅度大。

為了進一步體現實驗結果的真實可靠性，在UCI數據集上進行了實驗。表4給出3個算法在Breast、Shuttle和KDD Cup 3個數據集上的執行時間。從表中可以看出，當數據量較小時，所提算法在時間上的優勢并不明顯(以Breast數據集為例)，但是當數據量增大時，所提算法的優勢明顯體現出來并且隨著數據量的增大，這種優勢越明顯。為了保證算法執行結果的客觀性，在實驗過程中，對于Breast數據集，ODAVG算法和OMAGT算法的密度閾值Min P均設置為10;對于Shuttle數據集，ODAVG算法和OMAGT算法的密度閾值Min P均設置為120;對于KDD Cup數據集，ODAVG算法和OMAGT算法的密度閾值Min P均設置為200。對于區間段相似性閾值T，均設置為0.5。

表4 3種數據集的運行時間Tab.4 Execution time of the three datasets

3.4 檢測精確度對比

為了測試ODAVG算法的精確度，分別采用Dataset2、Shuttle和Breast3個數據集作為測試數據集，對ODAVG算法、OMAGT算法和LOF算法進行精確度測試。為了使結果較客觀，對每一個算法分別運行5遍，然后取平均值。在網格劃分時，ODAVG算法的每一維初始的區間段個數與OMAGT算法保持一致。檢測的精確度采用以下公式進行度量:

實驗結果如表5所示。通過表4可以看出:對于離群點較少的Shuttle數據集和Breast數據集，LOF算法的檢測精確度要高于ODAVG算法和OMAGT算法，且ODAVG算法的檢測精確度要高于OMAGT算法。對于Dataset2，由于離群點較多并且以較小類簇的形式出現，導致LOF算法的精確度相對較低，但是由于ODAVG算法和OMAGT算法刪除了大部分參與LOF算法運算的數據點，使得ODAVG算法和OMAGT算法的檢測精確度相對略高。在實驗過程中，對于DataSet2數據集，ODAVG算法和OMAGT算法的密度閾值M in P均設置為300;對于Shuttle數據集，ODAVG算法和OMAGT算法的密度閾值Min P均設置為120;對于Breast數據集，ODAVG算法和OMAGT算法的密度閾值Min P均設置為10。對于區間段相似性閾值T，均設置為0.5。

表5 3種算法的精確度Tab.5 Accuracy of the three algorithm s

綜上所述，從網格劃分效果來看，相對于OMAGT算法，ODAVG算法可以根據數據集的實際分布以更少的網格數目構建出與原始數據集分布一致的網格空間;從執行時間上來看，相對于OMAGT算法和LOF算法，ODAVG算法由于使用了可變網格的策略來處理大規模數據集，因此它能夠獲得較該兩種算法更高的執行效率，并且隨著數據量的增加，這種優勢會更加明顯;從檢測精確度來看，ODAVG算法能夠保持與OMAGT算法和LOF算法較一致的精確度。因此，文中所提出的ODAVG算法能夠在保證較高檢測精確度的同時，可以獲得更高的執行效率。

4 結語

離群點檢測是數據挖掘領域中一個重要的研究方向，并且在實際生活中有著廣泛的應用。文中提出了一種新的基于可變網格劃分的離群點檢測算法。該算法首先根據數據集的分布將空間劃分為大小不一的網格，然后刪除不可能成為離群點的數據點，最后對剩余的數據點執行LOF算法。相對于固定網格劃分的離群點檢測算法與LOF算法，該算法可以在保證正確率同時提高執行效率。但是，文中研究工作仍需要繼續進行，如在高維大規模數據集的執行效率是否可以進一步減少等。

［1］DUAN L，XU L，GUO F，et al.A local-density based spatial clustering algorithm with noise［J］.Information Systems，2007，32 (7):978-986.

［2］YUAN Y，ZHANG Y，CAO H，et al.New local density definition based on m inimum hyper sphere for outlier mining algorithm using in industrial databases［C］//Control and Decision Conference(2014 CCDC)，The 26th Chinese.Changsha:IEEE，2014: 5182-5186.

［3］Aggarwal C C，YU PS.Outlier detection for high dimensional data［J］.ACM Sigmod Record，2001，30(2):37-46.

［4］古平，劉海波，羅志恒.一種基于多重聚類的離群點檢測算法［J］.計算機應用研究，2013，30(3):751-753.

GU Ping，LIU Haibo，LUO Zhiheng.Multi-clustering based outlier detect algorithm［J］.Application Research of Computers，2013，30(3):751-753.(in Chinese)

［5］Breunig M M，Kriegel H P，Ng R T，et al.LOF:identifying density-based local outliers［J］.ACM Sigmod Record，2000，29(2): 93-104.

［6］王敬華，趙新想，張國燕，等.NLOF:一種新的基于密度的局部離群點檢測算法［J］.計算機科學，2013，40(8):181-185.

WANG Jinghua，ZHAO Xinxiang，ZHANG Guoyan，et al.NLOF:a new density-based local outlier detecting algorithm［J］.Computer Science，2013，40(8):181-185.(in Chinese)

［7］薛安榮，鞠時光，何偉華，等.局部離群點挖掘算法研究［J］.計算機學報，2007，30(8):1455-1463.

XUE Anrong，JU Shiguang，HEWeihua，et al.Study on algorithms for local outlicr detection［J］.Chinese Journal of Computer，2007，30(8):1455-1463.(in Chinese)

［8］ZHANG K，Hutter M，JIN H.A new local distance-based outlier detection approach for scattered real-world data［C］//Advances in Knowledge Discovery and Data Mining.Berlin，Heidelberg:Springer，2009:813-822.

［9］Pamula R，Deka J K，Nandi S.An outlier detection method based on clustering［C］//Emerging Applications of Information Technology(EAIT)，2011 Second International Conference on.Washington，DC:IEEE，2011:253-256.

［10］曹洪其，孫志揮.基于網格技術的高維大數據集離群點挖掘算法［J］.計算機應用，2007，27(10):2369-2371.

CAO Hongqi，SUN Zhihui.Algorithm of outliers mining based on grid techniques in high dimension large dataset［J］.Computer Applications，2007，27(10):2369-2371.(in Chinese)

［11］張天佑.基于網格劃分的高維大數據集離群點檢測算法研究［D］.長沙:中南大學，2011.

［12］Hsu CM，CHEN M S.Subspace clustering of high dimensional spatial data with noises［C］//Advances in Knowledge Discovery and Data Mining.Berlin，Heidelberg:Springer，2004:31-40.

［13］賀玲，蔡益朝，楊征.高維數據的相似性度量研究［J］.計算機科學，2010，37(5):155-156.

HE Ling，CAIYichao，YANG Zheng.Researches on similarity measurement of high dimensional data［J］.Computer Science，2010，37(5):155-156.(in Chinese)

［14］盛開元，錢雪忠，吳秦.基于可變網格劃分的密度偏差抽樣算法［J］.計算機應用，2013，33(9):2419-2422.

SHENG Kaiyuan，QIAN Xuezhong，WU Qin.Density biased sampling algorithm based on variable grid division［J］.Journal of Computer Application，2013，33(9):2419-2422.(in Chinese)

［15］王敬華，金鵬.基于粗約簡和網格的離群點檢測［J］.計算機工程與應用，2015，51(3):133-137.

WANG Jinghua，JIN Peng.Outliers detecting based on rough reduction and grid［J］.Computer Engineering and App lications，2015，51(3):133-137.(in Chinese)

［16］QIAN Xuezhong，SHENG Kaiyuan，QIAN Heng，et.al.An improved density biased sampling for clustering large-scale datasets［J］.Journal of Information and Computational Science，2014，11(7):2355-2364.

(責任編輯:楊勇)

An Ou tlier Detecting A lgorithm Based on the Variable G rid Division

MA Fei1，ZHU Changjie*1，ZHENG Ying1，DENG Jie2
(1.School of Computer Science and Technology，Huaibei Normal University，Huaibei 235000，China;2.School of Internet of Things Engineering，Jiangnan University，Wuxi214122，China)

As a widely used outlier detecting algorithm，the LOF algorithm usually spendsmuch time and space on the dealing with the large-scale dataset.The outlier detecting algorithm based on the stationary grid can solve the problems to some extent，but its implementation effect can be influenced by the granularity of grid division.Aiming at the problem，this paper proposes an outlier detecting algorithm based on the variable grid division.The proposed algorithm can dynam ically construct the grid space according to the practical distribution of data points in space，then remove all of the data points in the grid when it contains the count of data pointsmore than the threshold，finally execute the LOF algorithm in the remainder data points.The experimental results show that the proposed algorithm can receive a higher efficiency and accuracy compared with the outlier detecting algorithm based on stationary grid.

local outlier factor，outlier detection，variable grid，large-scale dataset

TP 301.6

A

1671－7147(2015)06－0751－07

2015－06－21;

2015－09－24。

安徽省高校自然科學研究項目(KJ2014B24)。

馬菲(1989—)，女，河南商丘人，軟件工程專業碩士研究生。

*通信作者:朱昌杰(1963—)，男，安徽懷寧人，教授，碩士生導師。主要從事人工智能與數據挖掘等研究。Email:840486167@qq.com