基于KPCA-W LSSVM的公共建筑能耗預測

許巧玲，林躍東，嚴哲欽

(福州大學節能技術研究中心，福建福州 350108)

基于KPCA-W LSSVM的公共建筑能耗預測

許巧玲，林躍東，嚴哲欽

(福州大學節能技術研究中心，福建福州 350108)

由于建筑能耗因子間存在非線性和高度冗余特性，傳統預測方法很難消除數據之間冗余和捕捉非線性特征，導致預測精度較低。為了提高建筑能耗預測精度，建立了一種基于KPCA-WLSSVM的建筑能耗預測模型。利用核主元分析(KPCA)對輸入變量進行數據壓縮，消除變量之間的相關性，簡化模型結構;進一步采用加權最小二乘支持向量機(WLSSVM)方法建立建筑能耗預測模型，同時結合一種新型混沌粒子群-模擬退火混合優化(CPSO-SA)算法對模型參數進行優化，以提高模型的預測性能及泛化能力。通過將KPCA-WLSSVM模型方法應用于某公共建筑能耗的預測中，并與WLSSVM、LSSVM及RBFNN模型相比，實驗結果表明KPCA-WLSSVM模型方法能有效提高建筑能耗預測精度。

建筑能耗;核主元分析;加權最小二乘支持向量機;模擬退火混合優化

隨著建筑能耗在我國能源消耗中所占比重的快速增長，建筑節能受到全社會越來越多的關注，準確有效地預測建筑能耗是開展節能評估工作的重要基礎，也是進行建筑節能優化設計的主要依據。由于建筑能耗系統涉及到機理復雜的熱濕傳遞過程，是一個典型的多變量、非線性、強耦合和多擾動的復雜系統，采用機理方法建立建筑能耗預測模型十分困難。人工神經網絡由于對非線性函數具有很強的擬合和逼近能力，作為一種有效的非線性建模方法，目前已有許多學者將其成功應用于建筑能耗預測領域［1-4］。但是由于神經網絡訓練基于經驗風險最小化原則，易產生過學習導致泛化能力下降，另外還存在諸如網絡結構難以確定和過分依賴大樣本學習等缺陷，因而在建筑能耗預測領域還難以大范圍推廣。

以統計學習理論為基礎的支持向量機(Support Vector Machines，SVM)［5-6］，不僅具有良好的非線性性能和泛化能力，而且與人工神經網絡相比具有小樣本學習能力強、學習推廣性能好以及高維數據處理能力強等特性，目前作為一種新的建模預測方法已在建筑能耗預測領域得到了廣泛應用［7-8］。

作為標準SVM的擴展，最小二乘支持向量機(Least Squares Support Vector Machines，LSSVM)將SVM的二次規劃問題轉化為線性方程組求解問題，在保留SVM一般特性的前提下，大大提高了學習速度，較好地解決了大樣本數據情況下SVM計算復雜的問題［9］。文獻［10］基于LSSVM回歸方法建立了建筑空調負荷模型，并獲得了較好的預測結果。

針對LSSVM丟失支持向量稀疏性的問題，Suykens等人［11］提出了加權最小二乘支持向量機算法(Weighted Least Squares Support Vector Machines，WLSSVM)。WLSSVM在建模過程中依據訓練樣本擬合誤差分別賦予其不同權重，從而克服了噪聲對LSSVM魯棒性能的影響。文獻［12］基于該算法建立了建筑冷負荷預測模型。

盡管支持向量機及其改進算法能夠有效處理高維數據建模問題，但是建筑能耗受到氣候條件、建筑特征參數、圍護結構熱工性能、室內熱擾、新風負荷、室內環境參數、空調運行模式等眾多因素的影響，且各因素之間嚴重相關，存在大量冗余信息，如果直接使用這些能耗數據用于SVM建模，則會導致模型的預測精度和泛化能力難以達到理想的結果［13-14］。因此，有必要在建立SVM預測模型前先對能耗數據進行特征提取和數據降維，最大限度降低數據中的冗余信息和噪聲，提高預測模型的泛化能力。

主元分析(PCA)和核主元分析(KPCA)方法均屬于一類用于數據壓縮和信息抽取的多元統計分析方法。但是PCA只是一種線性降維技術，它忽略了過程數據中可能存在的非線性信息。然而包括建筑系統在內的絕大多數實際物理過程本質上是非線性的。KPCA是對PCA的非線性擴展，它采用非線性映射對過程數據進行變換，能夠有效處理非線性特征提取問題。

為了提高建筑能耗預測模型的精度和可靠性，文中基于KPCA和WLSSVM提出一種公共建筑能耗預測方法。通過機理分析確定建筑能耗主要影響因素的基礎上，采用KPCA方法對輸入變量進行特征提取，消除變量之間的相關性，降低輸入變量的維數，將新的特征信息作為WLSSVM模型的輸入變量，從而建立公共建筑能耗預測模型。考慮到LSSVM的正則化參數和核寬參數對模型擬合精度和泛化能力都有較大影響，利用混沌粒子群-模擬退火混合優化(CPSO-SA)算法對LSSVM的參數進行優化選擇，進一步提高模型的預測精度和泛化能力。最后對某一公共建筑的能耗進行預測，并與WLSSVM、LSSVM和RBF神經網絡的預測結果進行比較，結果表明KPCA-WLSSVM預測模型的性能優于其它3種預測模型。

1 KPCA-WLSSVM模型算法

1.1 核主元分析

通過非線性映射，KPCA方法首先將原空間xi=(i=1，2，…，N)映射到某個高維特征空間，之后再進行主元分析。高維特征空間的協方差矩陣R為

1.2 加權最小二乘支持向量機

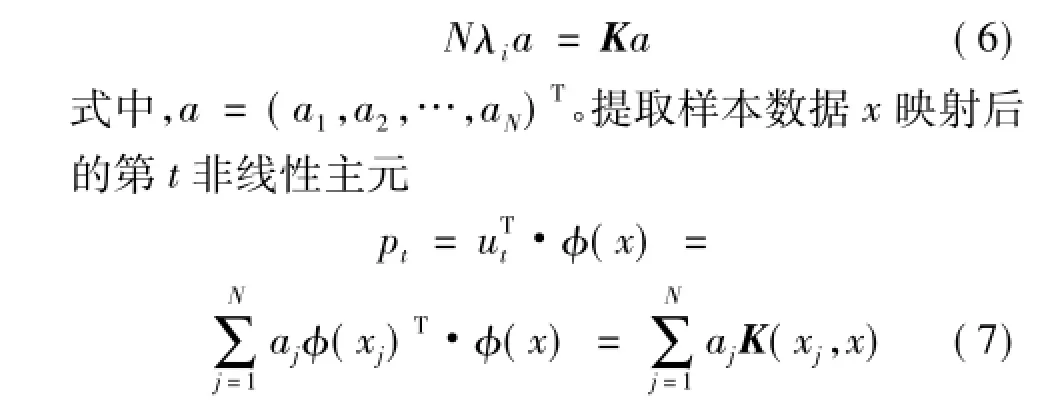
支持向量機是以統計學習理論為基礎而發展起來的一種機器學習方法，最小二乘支持向量機(LSSVM)不同于標準支持向量機的地方是它把誤差的二范數定義為損失函數，并將不等式約束改為等式約束，其優化問題為［15］

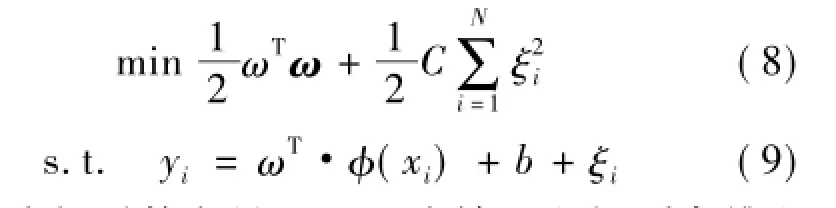
式中:ω為權系數向量;φ(·)為輸入空間到高維空間的映射;C為正則化參數;b為閾值。

同時，依據樣本訓練的重要性分別賦予其不同權重，以改善LSSVM魯棒性能欠佳的問題。對式(8)中誤差的二范數進行加權處理，設的權值為vi，則對應的優化問題變為

1.3 混沌粒子群-模擬退火混合優化算法

標準PSO算法以其簡單易行及快速收斂的特性在工程優化領域得到了快速發展，但也存在容易陷入局部最優問題，且搜索速度有待進一步提高。文中提出一種混沌粒子群-模擬退火(CPSO-SA)混合算法用于搜索最佳模型參數，該算法結合了CPSO算法的群體多樣性和SA算法的漸進收斂性優點，并保持全局搜索和局部搜索的平衡，可以有效提高算法的搜索效率，從而加快算法的收斂速度。

基于CPSO-SA的參數優化算法流程如下:

1)輸入訓練樣本集{(xi，yi)，i=1，2，…，N};設置CPSO-SA算法的控制參數:種群規模m、最大迭代次數tmax，初始溫度T=T0，終止溫度T=Tend;隨機產生m個粒子{p1，p2，…，pm}，初始化粒子的位置值和速度值。

2)計算每個粒子適應度值f(pi)。

3)比較當前粒子個體的適應度值，找出當前最優個體pbest，按式(16)的Logistic方程對pbest進行M次迭代，得到混沌變量可行解序列

式中:λ為控制參數;n為迭代次數。

4)進行PSO進化操作，即對粒子的速度和位置進行迭代進化，并獲得全局最優個體pBEST。

5)進行SA操作，取全局最優個體pBEST的一個領域值，記作best，計算

若Δf＜0，則更新pBEST，否則令s=exp(－Δf/T)，若s＞rand(0，1)，則更新pBEST，否則pBEST不變。

6)根據溫度下降函數T=T(t)，更新溫度T，若粒子溫度低于終止溫度Tend，則算法終止，粒子群全局極值個體參數即為最優參數C*和σ*，否則返回5)，進行下一步。

2 基于KPCA-WLSSVM建筑能耗預測

2.1 建筑能耗影響因素分析

建筑能耗系統是一個復雜的非線性系統，影響建筑能耗的因素眾多，主要分為4個方面:外部氣候條件、圍護結構、設備因素以及建筑運行管理模式:

1)外部氣候條件是影響建筑能耗的“自然”因素，包括溫度、濕度、日照及風速等參數，它們能夠直接影響熱量通過圍護結構的傳遞，進而對建筑能耗產生影響。

2)圍護結構可以看作是影響建筑能耗的“人為”因素，包括反映建筑熱工性能的圍護結構傳熱系數、遮陽率等參數和反映建筑體形特征的體形系數、建筑面積、朝向、窗墻比等參數，這類因素可以通過改善建筑本身的熱工性能及相關參數對建筑能耗起到積極作用。

3)設備因素，包括照度標準、燈具類型、設備功率等參數，這些參數取決于建筑的使用功能。

4)建筑運行管理模式也是影響建筑能耗的重要因素之一，它包括通風次數、人員密度、設備運行時間、新風指標等參數。

2.2 建模步驟

由于建筑能耗與眾多能耗影響因素之間存在復雜的非線性關系，并且能耗因子之間存在強相關性，在建模過程中直接影響能耗模型的預測精度。因此，文中首先利用KPCA提取能耗因子的非線性特征，消除數據冗余并降低模型輸入維數，然后采用WLSSVM方法建立能耗預測模型。模型結構如圖1所示。

圖1 KPCA-W LSSVM建模流程Fig.1 Sketch of KPCA-WLSSVM

考慮到LSSVM算法的正則化參數和核寬參數對模型擬合精度和泛化能力有較大影響［16］，文中采用1.3小節所述的CPSO-SA算法在正則化參數C及核寬參數σ的定義域內進行搜索，尋找C和σ的組合最優值。參數優化問題定義如下:其中:yi為第i個已知樣本的值;^yi為第i個樣本的模型輸出值，由預測模型計算獲得;J為正則化參數C及核寬參數σ的函數。

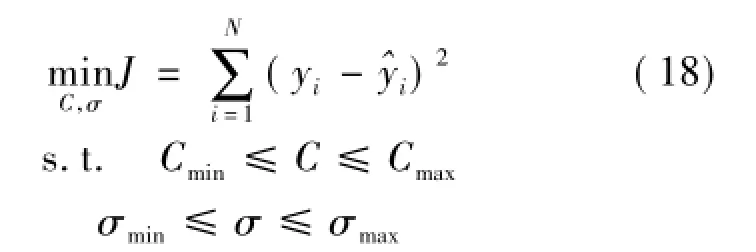
綜上所述，基于CPSO-SA優化的KPCAWLSSVM建筑能耗預測模型算法關鍵步驟總結如下:

1)樣本數據歸一化處理:為了避免計算出現飽和現象，按式(19)對建筑能耗訓練樣本進行歸一化處理:

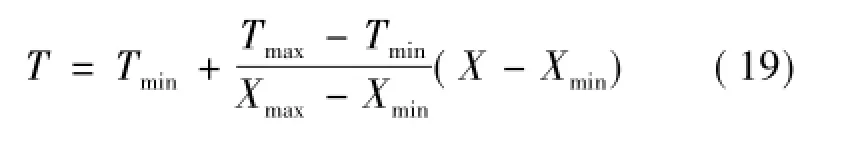
式中:X為原樣本數據;Xmax，Xmin分別為樣本數據中最大值和最小值;T為目標數據;Tmax為目標數據的最大值，取Tmax=0.9;Tmin為目標數據的最小值，取Tmin=0.1。

2)KPCA特征提取:按式(7)提取主成分，降低樣本維數，消除變量之間的相關性。

3)最優模型參數確定:初始化CPSO-SA粒子種群，每個粒子由C和σ組成;根據1.3小節步驟3)～6)獲得LSSVM模型的最優參數C*和σ*。

4)基于最優參數C*和σ*，由式(14)求解b，α*，建立WLSSVM建筑能耗預測模型。

6)反歸一化:按式(20)對模型輸出進行反歸一化處理:

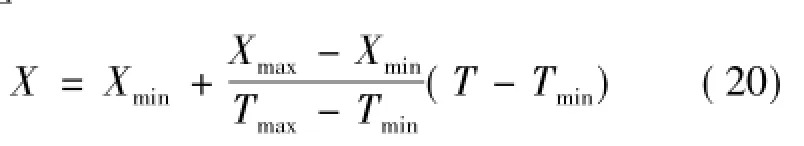
7)模型預測性能評價:采用相對誤差絕對值最大值Emax、相對誤差絕對值平均值Eave和均方根誤差RMSE 3個性能指標對模型進行評價:

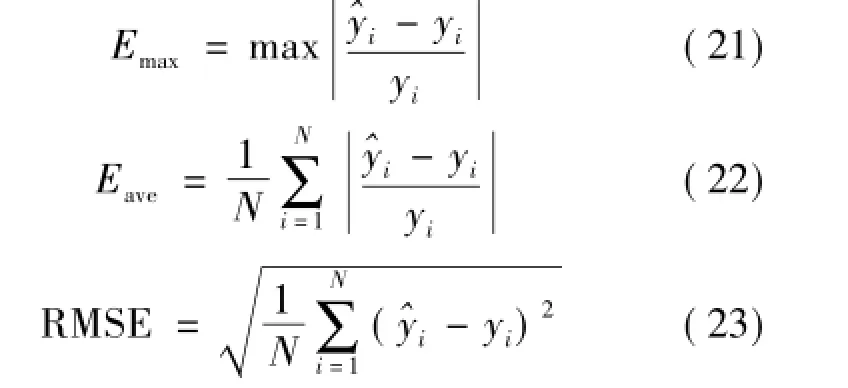
式中，N為樣本數。

2.3 實例分析

2.3.1 建筑物簡介基于南方地區一幢16層的公共建筑，采用文中所提KPCA-WLSSVM方法建立該建筑能耗預測模型。建筑物外形如圖2所示。

圖2 建筑外形示意Fig.2 Shape of an office building

該建筑總高度為57.4 m，主樓地上16層，地下1層，附樓(裙房)3層。建筑空調運行時間為8:00到17:00，總計每天運行9 h，空調季為6月1日到8月30日。總建筑面積為19 700.5 m2。地上建筑面積17 315.62 m2，地下建筑面積2 384.88 m2，標準層層高3.5 m，外窗尺寸為2.5 m×2.0 m，窗臺離地高度0.8 m。

2.3.2 構造樣本集根據能耗影響因素分析，結合《公共建筑節能設計標準》相關規定，文中在對公共建筑能耗建模過程中，主要考察以下能耗因子:最低照度(x1)，燈光熱擾(x2)，溫度(x3)，濕度(x4)，設備熱擾(x5)，電熱轉換率(x6)，人均新風指標(x7)，家具系數(x8)，外墻傳熱系數(x9)，內墻傳熱系數(x10)，玻璃遮陽系數(x11)，玻璃傳熱系數(x12)，通風次數(x13)［17］。

同時為減少試驗次數，并保證試驗的全面性，采用正交試驗方法獲取數據樣本集。DEST中影響因素的取值采用事先設定好的水平值，每個因素選取3個水平值，選用L27(313)正交表進行試驗計算，建筑物能耗的基準值采用動態負荷計算軟件DEST-C的計算值。為獲得較為理想的訓練數據，文中選用4組正交試驗，并且每組正交試驗中每個因素選取不同的水平值，經過DEST-C動態計算，獲得建筑物全年能耗結果。經DEST-C計算獲108組實驗數據，隨機取其中的3/4作為訓練樣本，余下的1/4作為測試樣本驗證模型的預測性能。

2.3.3 模型訓練通過KPCA計算，取主元個數為7個，此時累計貢獻率已經超過90%。碎石圖如圖3所示。另外，核參數和正則化參數是WLSSVM性能的重要影響因素，不同的參數組合將得到不同的學習性能和泛化性能。

為避免主觀經驗選取的盲目性，文中采用CPSO-SA算法對模型的兩個參數進行尋優，優化后的參數分別為C=378.3，σ=0.9，滿足預測模型對精度的要求，建筑能耗模型訓練結果如圖4所示，擬合值和期望值基本吻合。

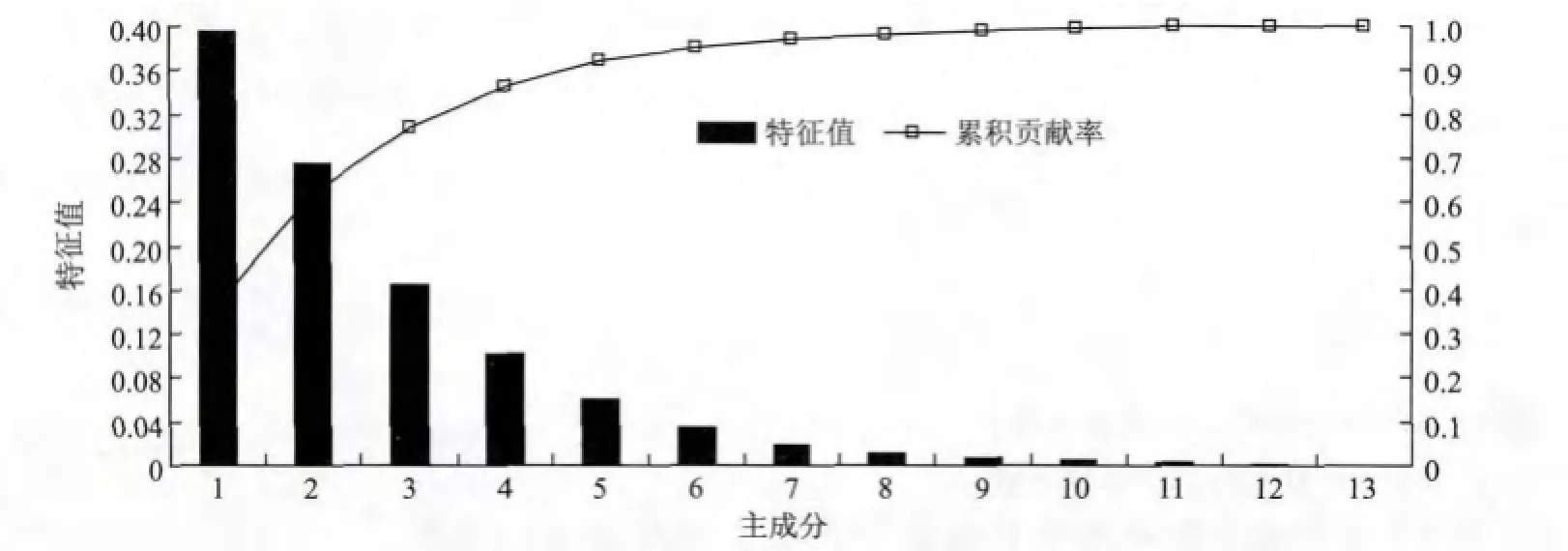
圖3 核主成分碎石Fig.3 Scree plot of the kernel p rincipal component

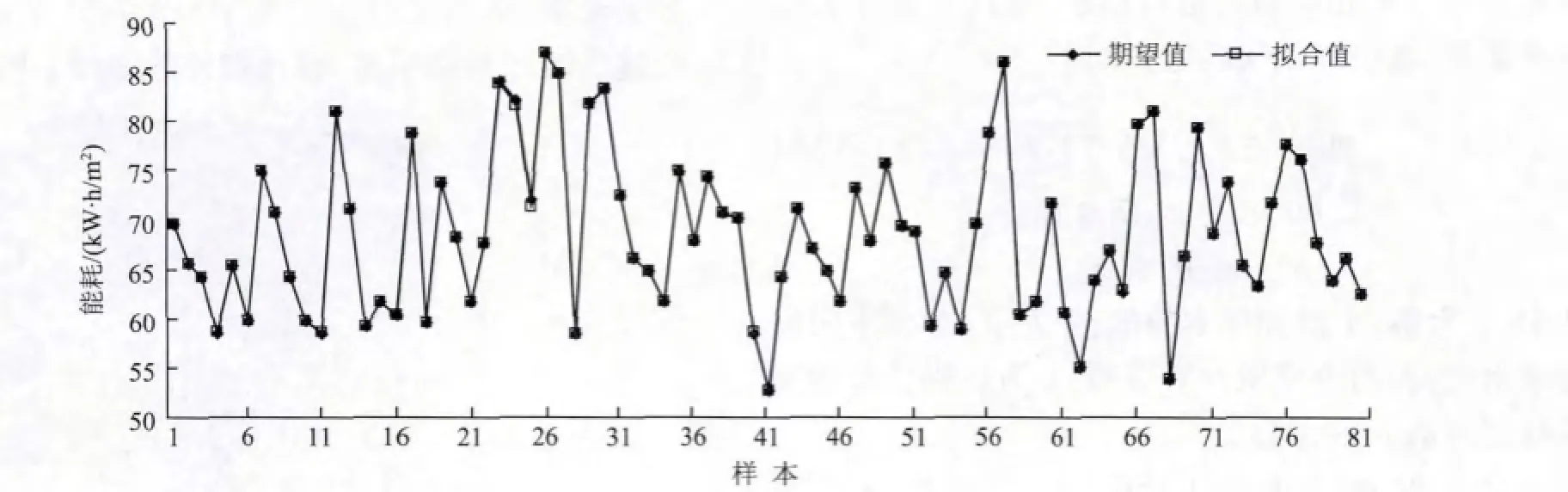
圖4 KPCA-W LSSVM模型訓練結果Fig.4 T raining resu lts of KPCA-W LSSVM

2.3.4 結果與分析為比較分析組合模型的預測效果，文中同時建立了LSSVM、WLSSVM和RBFNN神經網絡模型對建筑能耗進行預測。通過Matlab平臺實現上述4種預測模型對建筑能耗進行預測，預測值和實際值的對比如圖5所示。從圖中可以知道，4種模型的預測結果大都能夠反映能耗的變化，但有個別樣本點偏差較大，組合模型的預測值和期望值基本重合，相比于單一的LSSVM、WLSSVM和RBFNN神經網絡模型，組合預測模型的預測效果較好。

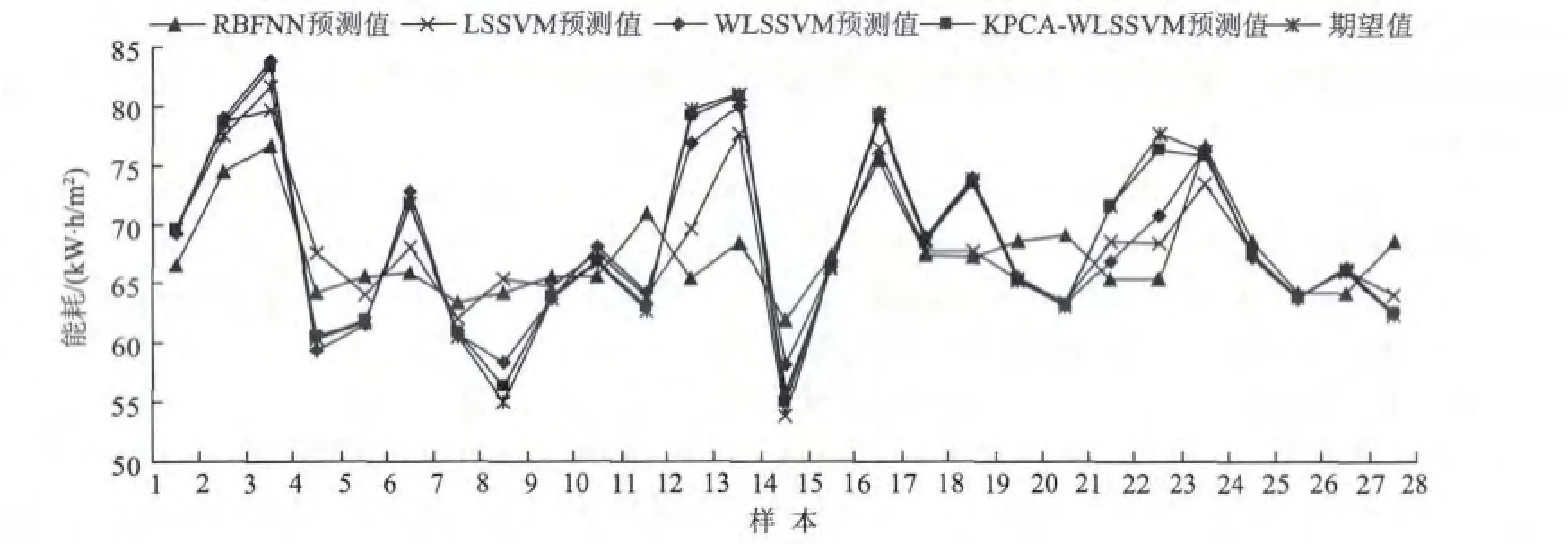
圖5 4種模型的預測結果Fig.5 Prediction of four models

為了從整體上評價4種預測模型的預測精度和穩定性，按式(21)、(22)及(23)對上述4種模型進行評價，4種模型預測結果的Emax，Eave，RMSE如表1所示。

表1 4種模型評價指標計算結果Tab.1 Prediction of four models

從表1的計算結果可以看出，采用RBF神經網絡和LSSVM方法預測雖然具有很高的訓練精度，但是當其用于預測時，誤差較大，泛化性能差，預測效果不理想;采用WLSSVM進行預測，平均預測誤差和均方根誤差比LSSVM有所降低，但預測效果仍有待提高。經過KPCA處理后，WLSSVM模型的預測效果得到了很大改善，最大相對誤差絕對值從8.84%降到2.98%，相對誤差絕對值平均值從1.43%降低到0.94%，表明組合模型具有更高的預測精度和預測穩定性，泛化能力得到顯著提高。

通過對比分析模型的性能指標，結果表明KPCA-WLSSVM模型具有更好的預測效果，是一種有效、可行的建筑能耗預測方法。

3 結語

在上述建筑能耗預測實例中，通過4個模型的預測結果及性能評價指標的比較可以看出，基于KPCA-WLSSVM能耗預測模型的預測效果要優于其它3種模型，表明KPCA-WLSSVM模型在建筑能耗預測中的有效性和優越性。主要結論如下:

1)通過KPCA提取輸入樣本的特征信息，消除建筑能耗影響因素間的冗余性和共線性，簡化模型的輸入樣本。

2)采用混沌粒子群模擬退火混合優化算法對模型的參數進行優化選擇，進一步提高建筑能耗預測模型的學習精度和推廣應用能力。

3)采用WLSSVM模型方法充分考慮了樣本對建模的影響，通過賦予建模樣本合適的權值，優化了LSSVM模型性能，使得模型具有良好的非線性處理能力。

通過KPCA方法與WLSSVM模型的有機結合，為建筑能耗預測提供了一種更為準確的途徑，為實現建筑節能分析打下了良好基礎。

［1］WONG S L，WAN K K W，Lam T N T.Artificial neural networks for energy analysis of office buildings with daylighting［J］.Applied Energy，2010，87(2):551-557.

［2］Azadeh A，Ghaderi S F，Tarverdian S，et al.Integration of artificial neural networks and genetic algorithm to predict electricalenergy consumption［J］.Applied Mathematics and Computation，2007，186(2):1731-1741.

［3］喻偉，李百戰，楊明宇，等.基于人工神經網絡的建筑多目標預測模型［J］.中南大學學報:自然科學版，2012，43(12): 4950-4955.

YUWei，LIBaizhan，YANGMingyu，et al.Buildingmulti-objective predictingmodel based on artificial network［J］.Journal of Central South University:Science and Technology，2012，43(12):4950-4955.(in Chinese)

［4］Mathieu JL，Price P N，Kiliccote S，et al.Quantifying changes in building electricity use，with application to demand response［J］.IEEE Transactions on Smart Grid，2011，2(3):507-518.

［5］Vapnik V.The Nature of Statistical Learning Theory［M］.New York:Springer，2000.

［6］Cortes C，Vapnik V.Support vector networks［J］.Machine Learning，1995，20(3):273-297.

［7］DONG Bing，CAO Cheng，Lee SE.Applying support vectormachines to predict building energy consumption in tropical region［J］.Energy and Buildings，2005，37(5):545-553.

［8］LIQiong，MENG Qinglin，CAI Jiejin，et al.Applying support vector machine to predict hourly cooling load in the building［J］.Applied Energy，2009，86(10):2249-2256.

［9］Suykens JA K，Van G T，De B J，etal.Least Squares Support Vector Machines［M］.Singapore:World Scientific，2002.

［10］LIXuemei，SHAO Ming，DING Lixing，et al.Particle swarm optimization-based Ls-Svm for building cooling load prediction［J］.Journal of Computers，2010，5(4):614-621.

［11］Suykens J A K，De Brabanter J，Lukas L，et al.Weighted least squares support vector machines:robustness and sparse approximation［J］.Neurocomputing，2002，48(1/4):85-105.

［12］GUO Yin，Nazarian E，Ko J，et al.Hourly cooling load forecasting using time-indexed arx models with two-stage weighted least squares regression［J］.Energy Conversion and Management，2014，80:46-53.

［13］LIQiong，MENGQinglin，CAIJiejin，etal.Predicting hourly cooling load in the building:a comparison of support vectormachine and different artificial neural networks［J］.Energy Conversion and Management，2009，50(1):90-96.

［14］Crawley D B，Hand JW，Kummert M，et al.Contrasting the capabilities of building energy performance simulation programs［J］.Building and Environment，2008，43(4):661-673.

［15］Suykens JA K.Least squares support vectormachines［J］.Neural Processing Letters，1999，9(3):293-300.

［16］樊曉雪.最小二乘支持向量機的參數選擇［D］.保定:河北大學，2012.

［17］康一亭，于丹，蘇華，等.辦公建筑能耗基準中影響因子對建筑能耗的影響度［J］.中南大學學報:自然科學版，2012，43 (S1):146-150.

KANG Yiting，YU Dan，SU Hua，et al.Impact factors of energy consumption benchmarking in office buildings［J］.Journal of Central South University:Science and Technology，2012，43(S1):146-150.(in Chinese)

(責任編輯:楊勇)

Prediction for Energy Consum ption of Public Building Based on KPCA-W LSSVM

XU Qiaoling，LIN Yuedong，YAN Zheqin
(Research Center of Energy Saving Technology，Fuzhou University，Fuzhou 350108，China)

There are highly redundant features in affecting factors of building energy consumption，and the traditional method has low preditive accuracy.In order to improve the accuracy of building energy consumption forecasting，A predictionmodel based on KPCA-WLSSVM is proposed to forecast building energy consumption.The kernel principal component analysis(KPCA)method could not only solve the linear correlation of the input and compress data but also simply the model structure.A novel hybrid chaos particle swarm optimization simulated annealing(CPSO-SA) algorithm is applied to optimize theWLSSVM parameters to improve the learning performance and generalization ability of themodel.Furthermore，the KPCA-WLSSVM model is app lied to the energy consumption prediction for an office building，and the simulation results show that the KPCA-WLSSVM has better accuracy compared with WLSSVM model，LSSVM model and RBF neural network model，which is considered that the KPCA-WLSSVM is effective for building energy consumption prediction.

energy consumption of building，kernel principal component analysis，WLSSVM，CPSO-SA

TU 111.19+5

A

1671－7147(2015)06－0710－07

2015－08－18;

2015－10－16。

國家自然科學基金項目(60804027，61374133);福州大學科研基金項目(FZU－022335，600338，600567);高校博士點專項科研基金項目(20133314120004)。

許巧玲(1956—)，女，福建福州人，教授，碩士生導師。主要從事過程優化、最優控制研究。

Email:zhhqxu@163.com