基于不確定性描述的云化Markov鏈狀態預測方法

查 翔，倪世宏，謝 川，張 鵬

（空軍工程大學航空航天工程學院，陜西西安710038）

基于不確定性描述的云化Markov鏈狀態預測方法

查 翔，倪世宏，謝 川，張 鵬

（空軍工程大學航空航天工程學院，陜西西安710038）

針對Markov鏈在預測概率發生跳變時無法有效地衡量樣本歸屬程度的問題，提出一種云化Markov鏈的狀態預測方法，通過云模型描述和處理樣本的不確定性。該方法將劃分的狀態區間視作一種概念，利用云模型對其進行云化表示，據此計算樣本對各概念的確定度，得到概念之間的概率轉移矩陣，從而實現帶有隨機特性的狀態預測。概念轉移概率作為關鍵隨機變量，對其進行了核密度估計。最后以多次隨機實驗的概率和提取代表性轉移概率分別給出了仿真實驗結果，表明該不確定性描述的預測方法在解決Markov鏈預測概率跳變現象的同時，可通過確定度的分配有效地表述樣本的歸屬程度，具有較好的實用性。

不確定性；Markov鏈；云模型；預測

0 引 言

時間序列的衍變過程蘊含著多種不確定性，通常運用隨機過程來模擬、分析和處理這一類問題。針對隨時間變化的動態變量預測，基于Markov鏈模型的狀態預測是一個較好的選擇［1］。與點預測［23］不同，Markov鏈模型實現的是定性預測，通過將樣本劃分多個狀態區間，對每個區間賦予帶有自然含義的概念，預測結果屬于狀態區間的范疇，從而可將該模型得到的結果歸結為一種定性結論。

然而，這種定性預測方法在定量數據發生微小波動時可能會引起預測狀態概率的跳變，即由某一狀態變換到另一狀態時，概率變化幅度過大，狀態轉移的過程不穩定。一般而言，事物發展若是平穩的，相應的隸屬狀態的概率也應是漸進變化的。產生這種現象的本質原因在于狀態區間的劃分過于明確，屬于一種確定性的分析方法。文獻［4］根據輸入樣本的激活強度決定是否采取硬或軟劃分，從而建立不同情形的Markov鏈狀態空間，但該方法對每種情形下的Markov狀態空間單獨進行討論，未實現真正意義上的軟化。文獻［5］提出了一種加權Markov模型，將明確狀態下的劃分矩陣拓展為模糊劃分矩陣，但需事先確定樣本對模糊狀態的隸屬度分配（即確定隸屬度函數的形式）。文獻［6］通過引入Dempster-Shafer（DS）證據理論建立了一種信度Markov模型，由基本概率指派函數（basic probability assignment，BPA）所指定的基概率數可類比模糊隸屬度，但仍屬于一次精確性的方法；它需根據應用背景設計相應的BPA，雖然存在較大的靈活性，但未提及可參考設計的理論和方法，實現起來較為困難。

以上方法在解決預測概率的跳變現象時，均需要通過為已知樣本指定精確的隸屬度來衡量和表述樣本的歸屬程度，但這一方式缺乏可參考的依據，預測結果的不可預知性成為難以回避的問題。為此，本文考慮引入不確定性人工智能中的云理論，提出一種基于不確定性描述的云化Markov鏈狀態預測方法，以云理論中的確定度類比隸屬度，利用區間云化以及概念確定度的分配描述和處理對象的不確定性，并使這種不確定性能貫穿方法的始終。該方法既能彌補Markov鏈的預測概率發生跳變這一缺陷，又避免了隸屬度函數或BPA的設計問題，并且可獲得隨機描述的預測概率。它在繼承模糊理論和信度Markov鏈優點的同時，將不確定性融入Markov鏈中進行研究，取得了較理想的實驗結果。

1 基于Markov鏈理論的狀態預測

Markov鏈是一類特殊的時間和狀態均離散的隨機過程，主要特征在于它的無后效性（即馬氏性）［79］。確切地說，已知隨機過程在“當前”時刻所處狀態的前提下，可以確定其“未來”時刻的狀態概率分布，而這一概率分布與“歷史”狀態無關。Markov鏈的嚴格定義由條件概率分布函數給出。

定義1 對于一離散隨機過程｛Z（t）｝以及離散時間集T＝｛0，1，2，…｝，t∈T，設｛Z（t）｝定義在概率空間（Ω，Γ，P）上且具有可數狀態空間E，滿足?t∈N＋以及i1，i2，…，in∈E，有

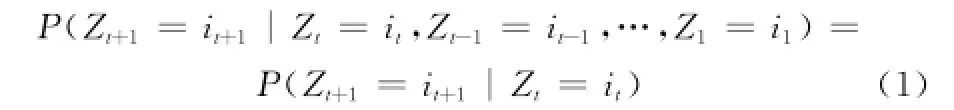
則稱滿足式（1）條件分布函數的離散隨機過程為Markov鏈，這一性質也被稱作馬氏性。Markov鏈簡化的表達形式為

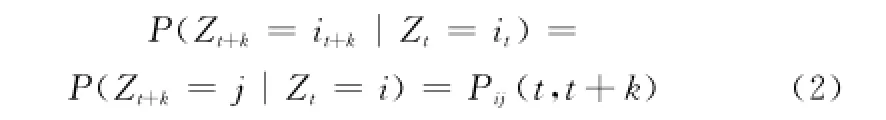
在式（2）中，Pij（t，t＋k）表示隨機過程在t時刻處于狀態i的條件下，在t＋k時刻轉移至狀態j的概率。若k＝1，則構造一步狀態轉移矩陣P＝（pij）m×m，其中，m為劃分的狀態數，pij由狀態轉移頻數矩陣確定，滿足1，2，…，k）。當k＞1時，可類似構造多步狀態轉移矩陣P，通過Chapman-Kolmogorov方程計算得到。本文主要利用一步狀態轉移矩陣建立Markov鏈預測模型。

應用Markov鏈分析和解決問題的首要前提是隨機過程必須符合馬爾可夫性，需要作馬氏性檢驗，具體過程可參考文獻［10］。另外，Markov鏈預測方法中一個關鍵問題是如何實現區間的劃分，每個區間對應一個Markov狀態，常用的劃分方法有經驗法、均值-方差法、平行曲線法以及聚類分析法等，需根據具體應用合理選取。

2 面向預測的不確定性云化Markov鏈預測方法

2.1 實現思路

不確定性建模方法主要從兩個方面體現：一是模糊性，從概念的區分程度來反映；二是隨機性，可體現在結果的表達形式上。現有的模糊集［45］、DS證據理論［6］等建模方法仍然集中在精確的隸屬度（或概率指派）上，不論樣本屬于一種或多種狀態，其隸屬程度在整個建模過程保持不變，這與模糊的思想是相悖的，為對象分配的隸屬度應圍繞某一中心值做微小波動，直接表現為具有穩定傾向的隨機數；并且模糊性與隨機性之間常具有很強的關聯性，這一規律不能被簡單忽略。文獻［11］提出的云模型可有效地描述和處理概念的這種不確定性，能夠表達兼有模糊性和隨機性的定性概念，在群智能優化［12］、模式識別［13］以及綜合評價［14］等領域應用廣泛。

本文首先根據所獲得的定量數據進行區間劃分，將每個區間視為一種狀態概念，把精確的數值合理轉換成有限個定性語言值；通過融合云模型對區間進行描述并建立云劃分，用以表達每個特定區間內數值本身的不確定性，并在此基礎上求解概念之間的概率轉移矩陣，進一步實現Markov鏈的狀態預測。

2.2 基于云的區間概念描述

云是某個定性概念與其定量表示之間的一種不確定性轉換模型，構成了定性與定量之間的相互映射，其定義如下［11］：

定義2 設U是用精確數值表示的定量論域，C為U上的一個定性概念，若U中的定量值x為定性概念C的一次隨機實現，那么x對C的確定度y＝μC（x）∈［0，1］是具有穩定傾向的隨機數，則稱在論域U上（x，y）的分布為云，（x，y）為其中的一個云滴。

云的數字特征反映了定性概念的整體定量特性，即期望Ex、熵En和超熵He，其中，Ex表示云滴在論域空間分布的期望值，代表了定性概念的重心位置；En是定性概念隨機性以及亦此亦彼性的度量，En越大，可被概念接受的論域范圍越大，概念也就更為模糊；He為熵不確定性的度量，即熵的熵，體現了論域值隸屬于概念程度的凝聚性，其值間接反映在云的厚度上。根據這3個數字特征，語言集中各定性概念Ci的云模型可表示成Ci（Exi，Eni，Hei），實際中常使用正態云模型［1517］，本文也用來表示對應的狀態區間。

傳統Markov鏈所涉及的可數個狀態區間是確定的，即各區間邊界是精確不變的值，它們所代表的概念比較明確和獨立，但實際上人對概念區間的理解通常是較為模糊的，概念之間并沒有明確的界限，相鄰概念之間存在著過渡區域。例如將航空發動機的健康狀態劃分為5個：健康、亞健康、合格、異常以及故障，它們均是用定性語言表示的狀態或區間概念，對處于相鄰狀態邊緣的發動機不能確切指定所屬哪一個狀態，這也是符合實際的，以上狀態的劃分只是便于后續的評估。因此，本文考慮首先根據序列樣本的取值范圍進行狀態區間的硬劃分，對得到的每一區間用云模型進行概念描述，實現狀態區間的軟化與云化。與建立隸屬度函數的模糊集方法的區別在于，區間云模型的描述只需3個參數，可根據每一區間內的樣本分布規律靈活調整參數值；由于云模型本身的特點，采用正向正態云發生器［18-19］獲得的定量值對某一概念的確定度（隸屬度）具有隨機性而非常數，從而使Markov鏈的預測結果帶有不確定性。

假設已經對序列樣本｛X（t）｝進行了區間劃分，得到m個狀態區間的集合S＝｛Si｝，（i＝1，2，…，m）。根據云化方法的思想，將S視為一概念集C，對其中的每個概念利用云模型來刻畫，這樣共得到m個概念云，它們共同組成連續語言值上的云標尺，這樣就完成了由定量到定性的轉換過程。云標尺用來計算每個樣本相對于其上各云模型的確定度，其中各云的數字特征根據不同情形確定：

（1）若區間Si為雙邊有界（包括半開半閉、全閉以及全開區間情形），上、下確界分別為sup（Si）、inf（Si）。此時為Si建立正態云Ci＝（Exi，Eni，Hei），Exi自然地用區間的中值表示，即Exi＝［sup（Si）＋inf（Si）］／2；根據正態云的“3En規則”［13］，對定性概念Ti有貢獻的云滴主要集中在區間［Exi－3Eni，Exi＋3Eni］內，那么近似有

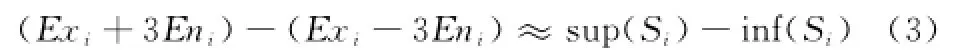
即Eni≈［sup（Si）－inf（Si）］／6，并以此作為Eni的計算式；Hei＝ci，其中，ci為一常數，根據變量本身的模糊度和隨機度經驗調整。ci越大，云滴離散程度越大，概念越模糊，算法會失去穩定性；ci越小，一定程度上會失去隨機性；當ci＝0時，云將退化為基本的正態分布。

（2）若區間Si為單邊有界，即上、下確界只存其一，這種情況下Si只可能位于云標尺的兩端。此時為Si建立半梯形云Ci＝（Exi1，Exi2，Eni，Hei），它屬于一種綜合云，與正態云相比多出一個期望參數。首先根據已有的序列樣本或先驗知識大致給出另一未知的確界值，作為Exi2，然后按照情形（1）中雙邊有界區間的參數計算方式，由兩確界值分別計算Exi和Eni，則Exi1＝Exi，Hei仍取經驗常數ci。

2.3 云化Markov鏈預測方法的實現

云化方法將原劃分區間理解為狀態概念，要建立云Markov鏈預測模型，關鍵在于計算概念到概念之間的一步轉移概率，繼而得到一步概念轉移概率矩陣，仍然用P進行表示。為得到P，首先需要計算序列樣本相對于各概念云的確定度，用X條件云發生器［11］實現。對于不同的云類型，計算方法也有所區別。

2.3.1 多序列樣本多概念的確定度計算

設序列樣本x1，x2，…，xn∈｛X（t）｝，云標尺上各概念正態云Cj對應的數字特征為（Exj，Enj，Hej），將序列樣本xt看作Cj的一次隨機實現（t＝1，2，…，n；j＝1，2，…，m），那么xt對Cj的確定度μj（xt）計算方法為：

（1）對概念Cj，生成一個正態隨機數En′jt＝norm（Enj，He2j），其中，norm（·，·）為正態隨機數生成函數，以Enj為期望和Hej為標準差；

（2）將xt視為特定取值，得到其對概念Cj的確定度為

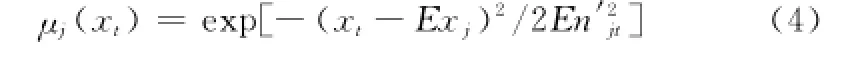
（3）對所有序列樣本以及每一概念云，重復上述過程，共得到m·n個確定度變量。

若概念對應的云為半梯形云，是一種組合云，數字特征與正態云相比有所不同，此時需要增加對xt所處位置的判別，不同位置得到的確定度不同。假設半梯形云Cj為左半升的，其對應的數字特征（Exj1，Exj2，Enj，Hej），那么xt對概念Cj的確定度μj（xt）分以下兩種情況計算：

（1）若xt≤Exj1，即xt位于Cj的上升部分，此時μj（xt）的計算方式同正態云；

（2）若Exj1＜xt≤Exj2，即xt位于Cj的平穩部分。根據半梯形云的特點，這一部分是上升部分的延續，考慮到確定度的最大值為1，此時μj（xt）不具備隨機性，μj（xt）≡1。

對于右半降的半梯形云Cj，其下降部分是平穩部分的延續，計算確定度的方法類似。

無論概念云為正態云或者半梯形云，根據計算步驟得到的所有確定度變量，共同構成序列樣本與概念之間的確定度矩陣V?（μj（xt））m×n。由于中間變量En′jt或y′是隨機的，因此μj（xt）并不是固定值，V構成一個隨機矩陣，這一現象體現了序列樣本與概念之間的不確定性轉換關系，這也是本文云化方法的一個特點。確定度矩陣V具的性質如下：

性質1 對固定的j和t，V中的元素μj（xt）并不為常數，服從某一特定分布；

前3條性質容易理解。對于任何一個定義在已有m個概念云范圍內的序列樣本，可同時屬于其中一個或多個概念云，但所有概念云下的確定度之和應該等于1，這也符合人的認知。然而由性質4可知，確定度矩陣V并不符合這一條件。為此，以單個序列樣本為對象，將該樣本下所有可能的確定度進行歸一化處理，即

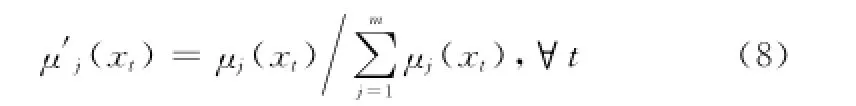
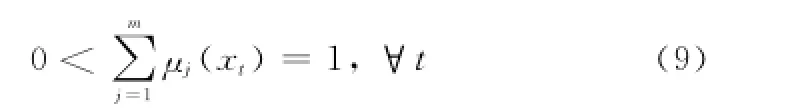
進一步地可推知

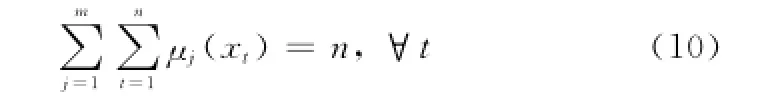
2.3.2 概念轉移概率矩陣的求解

概念轉移概率矩陣可視為云方法下Markov鏈概率轉移矩陣的一種擴展，可依據更新后的確定度矩陣V對其求解。設概念轉移概率矩陣P＝（pij）m×m，其中，pij為云Markov鏈模型中由概念Ci轉移到概念Cj的轉移概率，類比狀態轉移概率的定義，有

式中，μi（xt）（或μj（xt））代表序列樣本xt對概念Ci（或Cj）的確定度；n為樣本長度；m為概念總數。pij的含義是：“所有序列樣本由概念Ci轉移到Cj的確定度之和”與“所有序列樣本由概念Ci轉移到所有概念的確定度之和”的比值，滿足：pij≥0且

由式（11）可知，V中任意μi（xt）均是隨機的，以致pij在每次計算時都會變化，pij仍然構成隨機變量，有自己的統計性質。為簡單起見，假設所有概念云為正態云，聯立式（4）和式（11），得

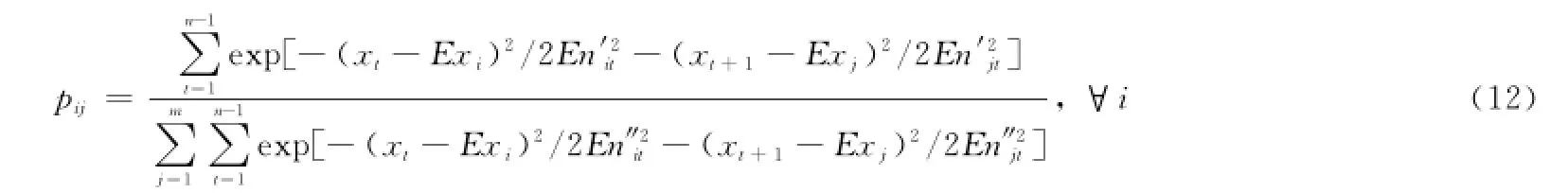
式中，En′it，En″it～N（Eni，He2i），En′jt，En″jt～N（Enj，He2j）（t＝1，2，…，n；j＝1，2，…，m）；對于每個xt，均存在不同的隨機變量En′it、En″it、En′jt和En″it，這樣分子和分母各包含2（n－1）個以及2m（n－1）個獨立的隨機變量，它們組成多維隨機矢量Q。將式（12）中出現的各xt、xt＋1、Exi、Exj均視為常量，那么復合隨機變量pij為Q的函數，記為

若不同的xt對應著同一個概念Ci（或Ci），那么此時En′it（或En′jt）服從同一參數下的正態分布。

要深入考察某一隨機變量的統計性質，常需要求解其概率密度函數，繼而得到各項數字特征（如期望、方差或各階距等）。以pij作為目標隨機變量，若將En′it或En′jt的正態概率密度函數代入式（12）中，易知pij的計算式含有嵌套的指數函數，很難得到具有解析形式的概率密度函數。對于這種情況，可利用Parzen窗方法對pij進行非參數的核密度估計［20-21］。該方法不需事先假定分布函數的形式，而是直接根據已知的樣本進行概率密度估計。核密度估計的函數＾f（x）可表示為

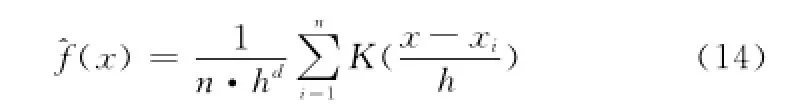
式中，n為樣本長度；h為窗的寬度；d為樣本維數；K（·）為核函數，本文采用Guass核函數另外，h的選擇采用式（15）固定形式［22］。

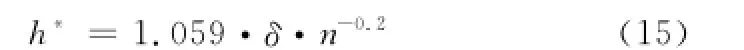
式中，δ為樣本的標準差。

2.3.3 目標概率分布向量的預測

在已知初始狀態概率分布的情況下，對未來時刻系統歸屬各概念的概率分布作出預測，進而根據各概念的預測概率值大小作出決策分析。設t時刻樣本xt對各概念的歸一化確定度為μ′j（xt）（j＝1，2，…，m），對應確定度矩陣V的第t列，將其轉置得到初始概率分布矢量π（t）＝（π1（t），π2（t），…，πm（t））。在求得概念轉移概率矩陣P之后，根據Markov鏈一步預測思想，計算t＋1時刻各概念的概率分布矢量π（t＋1）為

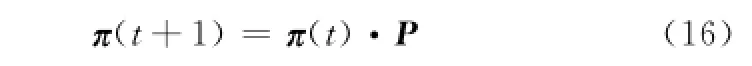
對于π（t＋1），依據最大概率原則取最大概率對應的概念作為最終的預測結果。由于矩陣P的隨機性，π（t＋1）相應地表現為隨機矢量，這體現出預測結果的不確定性，可進行多次試驗對結果進行統計分析。對于新獲得的樣本，可將其加入到原始樣本序列中，按前述方法對概念轉移概率矩陣實現更新。

3 仿真實驗

這一部分的實驗仍然基于文獻［6］中澳大利亞Monash大學Hyndman教授公開的測試樣本，以驗證本文方法的效果。

3.1 區間概念的描述及可視化

測試樣本共包含20期的庫存需求情況統計，并滿足Markov性。為了能與信度Markov模型有更好的可比性，本文按照同一方式，將序列樣本硬劃分為3個連續的狀態區間：［0，150），［150，200］，（200，＋∞］，分別用概念L、M和H表示，易知前兩個均為雙邊約束區間，而第3個為單邊約束區間。按照第2.1節云化區間概念的方法，設超熵He＝2，則各概念云的參數為C1（75，25，2），C2（175，8.33，2），C3（215，229，0.5，2）。通過正向云（正態云和半梯形云）發生器算法計算云滴的確定度，生成各概念云組成的可視化云標尺，如圖1所示。

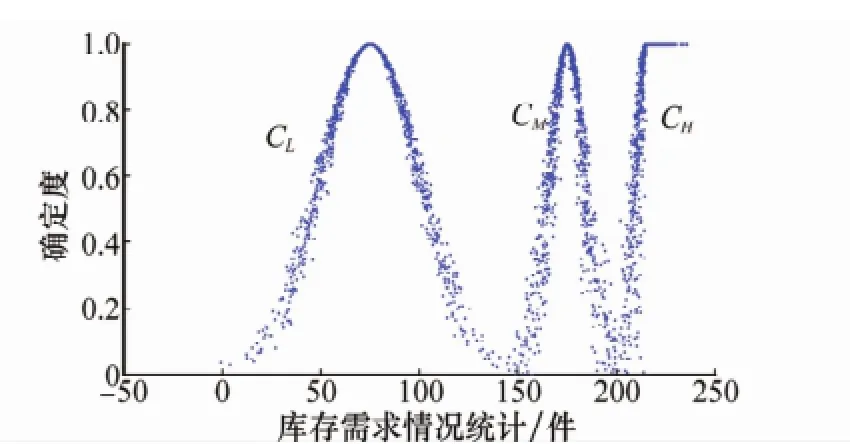
圖1 各概念的云標尺

云標尺圖實現了由定性概念到定量表示的過程，圖1直觀地給出了各區間上庫存需求情況統計的確定度分布情況：越靠近區間中心的樣本，歸屬于該區間概念的確定度越大（最大可為1），概念也就越清楚；越靠近區間交集部分的樣本，不同交集區間的確定度相對較小，且差異不大，概念也就越模糊。另外，任意樣本的確定度也是不確定的，并不是固定值，這恰能反映系統發展規律的動態性。因此，云化方法較好地體現出了建模的不確定性，能夠反映序列樣本的自身特點。

3.2 概念轉移概率的統計規律分析

概念之間的轉移概率屬于云化Markov鏈方法中關鍵隨機變量，但因其表達形式復雜，很難挖掘其變化規律。這里不妨以求解p12和p23為例進行說明，即由概念L轉移到概念M、概念M轉移到概念H的轉移概率，其他轉移概率的分析方法類似。由樣本及概念描述，n＝20，m＝3，則Q的維數為152。根據pij的定義，每次仿真下均會得到152個隨機確定度，它們仍然滿足性質4，并由此計算pij的值。對核密度估計而言，樣本越多，估計出的概率密度越接近真實情況，為此仿真500次，共得到500個pij的隨機取值，然后按照第2.3.2節的方法，畫出p12和p23的核密度估計曲線，如圖2所示。

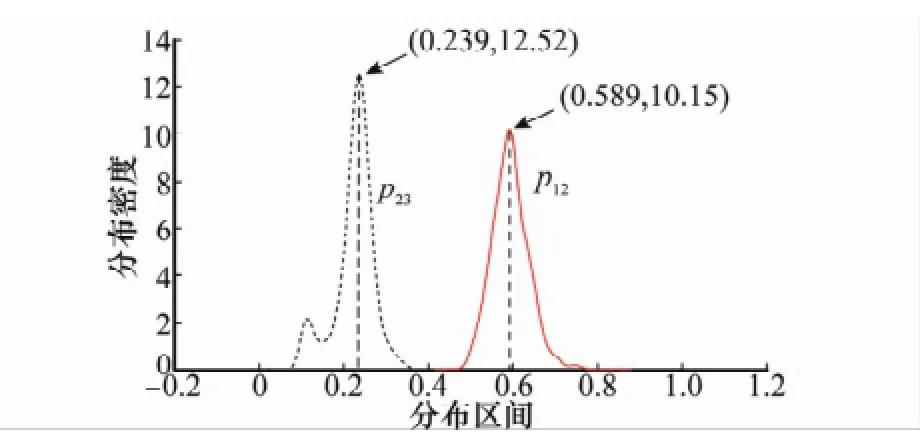
圖2 不同概念轉移概率的核密度估計曲線（He＝2）

圖2 說明了p12和p23的核密度估計曲線不同于正態分布的形式，而是呈現未知的特定分布，這與理論分析是一致的。由于各項確定度計算方法的差異，導致p12和p23的核密度估計曲線形式也有所區別，包括中心位置和對稱性等方面。

3.3 數據變動對結果的影響

隨機性為本文預測模型的特性之一，只進行一次實驗無法對其充分描述；另外，為說明最后一期（即第20期）的不同數值對預測結果的影響，將最后一期的數值（記為d（20））由197逐漸增加到204，并在每一數值下重復20次仿真實驗，預測第21期（記為d（21））的概率分布，如圖3所示。

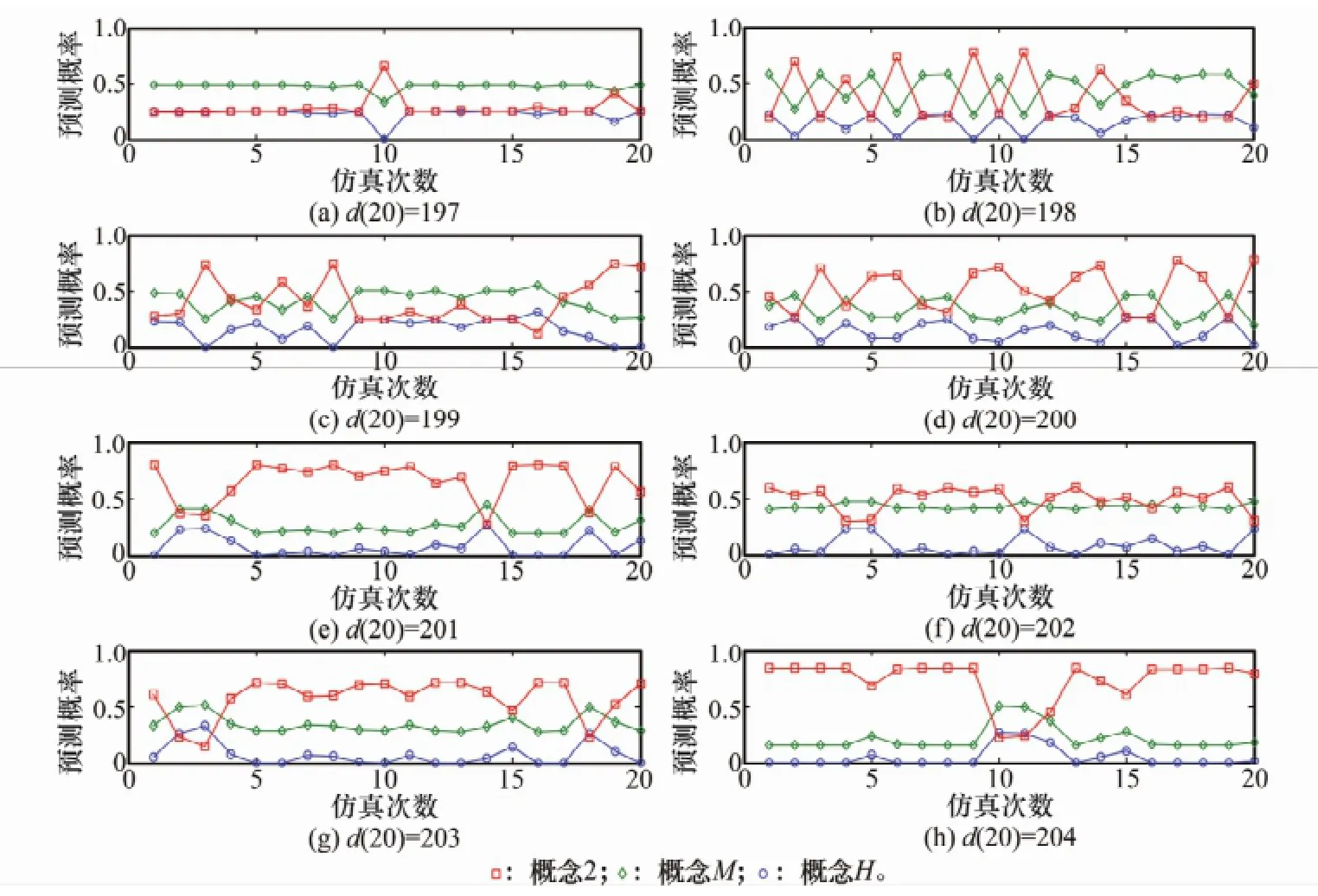
圖3 不同d（20）對結果的影響（重復20次實驗

在圖3中，預測第21期時對應的概率分別記為πL（21）、πM（21）以及πH（21）。可以看出，任意一幅子圖中，每次仿真下得到的結果是隨機的；d（20）＝197時，其距離狀態邊界相對較遠，歸屬狀態M的確定度與其他兩個概念的確定度差異較大（可從云標尺中反映出），幾乎總有πH（21）＜πM（21），πL（21）＜πM（21），隨機性對確定度的影響不很明顯。隨著d（20）的增加，其逐漸逼近狀態M和H的交界部分，對應著兩個概念比較明顯的混疊邊界，此時πM（21）整體下降，而πH（21）呈整體上升趨勢，兩者之間的差異逐漸縮小。如d（20）＝198以及d（20）＝199時，從圖3中已經很難判斷歸屬狀態M和H的概率差異，這是模型不確定性的原因所致。當d（20）進一步增加時，其逐漸遠離狀態M和H的交界部分，πH（21）繼續保持增加的趨勢，d（20）歸屬狀態H的程度更為明顯，如d（20）＝204時，概念H占主導地位，除了由于隨機性的原因少數情況出現πH（21）＜πM（21）。另外，最后一期的數值偏離概念L較遠，因此在數值變動范圍內πL（21）始終保持較小值。

為了更直觀地表明以上變化規律，將d（20）作為自變量，取值范圍為［195，204］，觀察第21期概率分布的變化情況，如圖4所示。對d（20）的每一取值，在確定概念轉移概率pij時，取其核密度估計曲線峰值對應的橫坐標值作為此概念轉移概率代表性的點，如根據圖2，可知p12＝0.589，p23＝0.239，以此進一步計算d（21）的預測概率。由于估計核密度曲線時所用樣本有限，不同取值樣本下得到的曲線存在稍許差異。

可以看到，當d（20）逐漸增加時，d（21）的各概念預測概率距呈現緩慢變化的趨勢，未出現概率跳變現象，達到了與信度Markov模型同樣的效果。根據極大概率判定的思想，當d（20）＝200時，d（21）歸屬的概念發生變化，由概念M轉變成概念H；而信度Markov模型則是在d（20）＝197時出現這一變化，這是由各模型本身的特點決定的。然而，本文方法有其獨特之處：模型的不確定性使得圖4的結果不唯一，即使采用核密度曲線中具有代表性的概率點，每次仿真時預測概率曲線仍有些許變動；并且某一概念下的曲線走勢可能非單調，如概念M先增后減，相比之下，信度Markov模型得到的各預測概率是確定的并且單調變化。

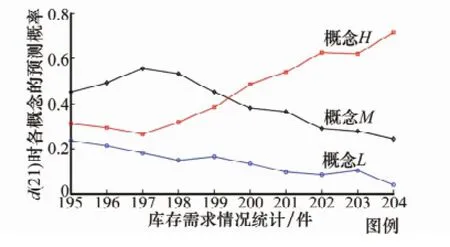
圖4 基于代表性轉移概率的d（21）預測概率曲線

3.4 不同超熵對結果的影響

若樣本已知，按第3.1節描述云概念的方法，云模型的期望和熵可唯一確定，而超熵為可變參數，它對云化Markov鏈的影響直接反映在概念轉移概率的計算上。超熵越大，pij的隨機性越大，分布范圍也就越廣。為了說明這一問題，圖5給出了He＝5時的核密度估計曲線，并與圖2進行對比。

根據圖5，p12和p23具有代表性的密度點分別為0.586和0.215，與He＝2時的取值（見圖2）相差不大，基于代表性轉移概率的d（21）預測概率曲線也不存在較大差異（He取其他值時情況類似）。雖然pij為未知解析形式的隨機變量，但云模型的超熵對其大體位置不會產生明顯影響，進而基于代表性轉移概率的預測概率也不會有較大變動。由此可推斷，本文方法具有較好的穩定性，對未知參數He不敏感。特別地，當He＝0時，核密度估計曲線僅為平行于縱軸的直線，即pij為一固定量。

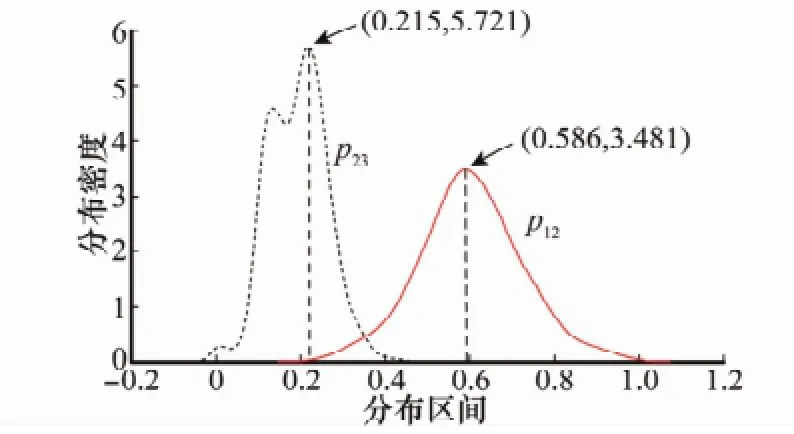
圖5 不同概念轉移概率的核密度估計曲線（He＝5）

綜上所述，基于不確定性描述的云化Markov鏈方法能夠克服數據的微小波動帶來的狀態跳變現象，能夠使各概念的預測概率保持漸進地穩定地變化規律；并且該方法實現過程簡單，只需根據樣本確定模型參數，不需指定模糊隸屬度函數或復雜的基本概率指派函數；結果信息豐富，具有隨機性特點；對不同的可變參數（超熵），根據基于代表性轉移概率得出的預測結果穩定性保持較好，預測概率受超熵影響不明顯。

4 結 論

在運用Markov鏈實現隨機過程的預測時，未來時刻的預測概率可能會出現跳變，以分配隸屬度為解決這一問題的手段，現有方法常缺乏有效依據，隨意性較大。本文借助于云模型這一新的處理方法，將其引入Markov鏈預測模型中，提出了一種基于不確定性描述的云化Markov鏈預測方法，主要體現在對狀態概念隨機性和模糊性的處理上。它將Markov鏈狀態空間采用云概念來表達，通過X條件云發生器獲得樣本對每一概念的隨機確定度，作為樣本歸屬某個概念的程度標量，以此為基礎求解概念轉移矩陣，進而實現Markov鏈的狀態預測；樣本確定度、概念轉移概率以至未來時刻的預測概率，均為不同分布下的隨機變量，較好地保持了模型不確定性的傳遞。對實驗結果的分析表明，基于不確定性描述的云化Markov鏈預測能夠解決數據微小波動帶來的狀態跳變問題，既不需要如模糊方法一樣指定具體的隸屬度函數，也可避免信度Markov模型設計BPA函數的問題，只需根據已有樣本求解少量的云參數，方法簡單且易于實現，可視為基本Markov鏈的一種擴展，具有較好的適應性。由于直接的實驗結果表現為隨機形態，本文僅簡單考慮了核密度曲線峰值位置點的代表性概率，如何對其統計分析并有效利用需作進一步地探究。

［1］Farahat W A，Asada H H．Estimation of state transition proba-bilities in asynchronous vector Markov processes［J］．Journal of Dynamic Systems，Measurement，and Control，2012，134（6）：1- 14．

［2］Li H L，Guo C H．Piecewise cloud approximation for time series mining［J］．Knowledge-Based Systems，2011，24（4）：492- 500．

［3］Shang Z G，Yan H S．Forecasting product design time based on fuzzy support vector machine［J］．Control and Decision，2012，27（4）：531- 541．（商志根，嚴洪森．基于模糊支持向量機的產品設計時間預測［J］．控制與決策，2012，27（4）：531- 541．）

［4］Xie D W，Shi S L．Mine water inrush prediction based on cloud model theory and Markov model［J］．Journal of Central South University，2012，43（6）：2308- 2315．（謝道文，施式亮．基于云理論與加權Markov模型的礦井涌水量預測［J］．中南大學學報，2012，43（6）：2308- 2315．）

［5］Dang X C，Hao Z J，Wang X J．Forecasting of user behavior based on fuzzy weighted Markov chain［J］．Journal of Lanzhou University，2011，47（1）：110- 115．（黨小超，郝占軍，王筱娟．模糊加權Markov鏈的用戶行為預測［J］．蘭州大學學報，2011，47（1）：110- 115．）

［6］Deng X Y，Deng Y，Zhang Y J，et al．A belief Markov model and its application［J］．Acta Automatica Sinica，2012，38（4）：666- 672．（鄧鑫洋，鄧勇，章雅娟，等．一種信度馬爾可夫模型及應用［J］．自動化學報，2012，38（4）：666- 672．）

［7］Singh S S，Chopin N，Whiteley N．Bayesian learning of noisy Markov decision processes［J］．ACM Trans.on Modeling and Computer Simulation，2013，23（1）：1- 25．

［8］Ghidini G，Das S K．Energy-efficient Markov chain-based duty cycling schemes for greener wireless sensor networks［J］．ACM Journal on Energy Technologies in Computing Systems，2012，8（4）：1- 32．

［9］Malikopoulos A A．Convergence properties of a computational learning model for unknown Markov chains［J］．Journal of Dynamic Systems，Measurement，and Control，2009，131（4）：1- 7．

［10］Alagoz O，Hsu H，Schaefer A J，et al．Markov decision processes：a tool for sequential decision making under uncertainty［J］．Medical Decision Making，2010，30（4）：474- 483．

［11］Li D Y，Du Y．Artificial intelligence with uncertainty［M］．Beijing：National Defense Industry Press，2005：143- 145．（李德毅，杜鹢．不確定性人工智能［M］．北京：國防工業出版社，2005：143- 145．）

［12］Wang W X，Wang X，Ge X L，et al．Muti-objective optimization model for muti-project scheduling on critical chain［J］．Advances in Engineering Software，2014，68（12）：33- 39．

［13］Jin B，Wang Y，Liu Z Y，et al．A trust model based on cloud model and Bayesian networks［J］．Procedia Environment Sciences，2011，11（12）：452- 459．

［14］Zhang L M，Wu X G，Ding L Y，et al．A novel model for risk assessment of adjacent buildings in tunneling environments［J］．Building and Environment，2013，65（4）：185- 194．

［15］Li H L，Guo C H，Qiu W R．Similarity measurement between normal cloud models［J］．Acta Electronica Sinica，2011，39（11）：2561- 2567．（李海林，郭崇慧，邱望仁．正態云模型相似度計算方法［J］．電子學報，2011，39（11）：2561- 2567．）

［16］Liu S，Chang X C．Synchro-control of twin-rudder with cloud model［J］．International Journal of Automation and Computing，2012，9（1）：98- 104．

［17］Li D Y，Liu C Y，Liu L Y．Study on the universality of the normal cloud model［J］．Engineer Sciences，2005，3（2）：18- 24．

［18］Qin K，Xu K，Liu F L，et al．Image segmentation based on histogram analysis utilizing the cloud model［J］．Computers and Mathematics with Applications，2011，62（7）：2824- 2833．

［19］Xu J Q，Bi Y M，Zhang X D，et al．Analysis of cost-capability for missile weapon based on cloudy model［J］．Systems Engineering and Electronics，2012，34（1）：91- 96．（徐加強，畢義明，張曉東，等．基于云模型的導彈武器費用 能力分析［J］．系統工程與電子技術，2012，34（1）：91- 96．）

［20］Kolomvatsos K，Hadjieftymiades S．On the use of particle swarm optimization and kernel density estimator in concurrent negotiations［J］．Information Sciences，2014，262（10）：99 -116．

［21］Malec P，Schienle M．Nonparametric kernel density estimation near the boundary［J］．Computational Statistics and Data Analysis，2014，72（10）：57- 76．

［22］Bolance C，Guillen M，Nielsen J P．Kernel density estimation of actuarial loss functions［J］．Mathematics and Economics，2003，32（9）：19- 36．

Cloud-transforming method of Markov chain state prediction based on uncertainty description

ZHA Xiang，NI Shi-hong，XIE Chuan，ZHANG Peng
（College of Aeronautics and Astronautics Engineering，Air Force Engineering University，Xi’an 710038，China）

To deal with ownership degree of samples in Markov chain effectively facing with a skip of the predicted probability，a cloud-transforming method of Markov chain state prediction is proposed．Samples’uncertainty is described and processed by using the cloud model．Regarded as a kind of concept，the partitioned state intervals are expressed based on the cloud model，and further the certainty of each objective to all concepts is computed．Then to realize stochastic state prediction，the concept transfer matrix is calculated．The kernel density estimation of concept transfer probability is obtained considering its significance．Finally simulation results are given in form of probability of repeated tests and extracted representative transfer probability，and it shows that the uncertain method can both avoid a skip of the Markov chain predicted probability and measure ownership degree of samples effectively，and is more practical as well．

uncertainty；Markov chain；cloud model；prediction

O 211．62

A

10．3969／j．issn．1001-506X．2015．04．34

查 翔（1988-），男，博士研究生，主要研究方向為飛機狀態監控與故障診斷、人工智能及其應用。E-mail：zha_xiang＠126．com

倪世宏（1963-），男，教授，博士研究生導師，主要研究方向為飛行數據智能處理。E-mail：470474069＠qq．com

謝 川（1974-），男，副教授，博士，主要研究方向為飛行數據智能處理。E-mail：1830486912＠qq．com

張 鵬（1982 ），男，講師，博士，主要研究方向為飛機故障診斷、故障預測與健康管理。E-mail：zhangpeng25＠gmail．com

1001-506X（2015）04-0942-07

2014- 07- 15；

2014- 10- 16；網絡優先出版日期：2014- 11- 05。

網絡優先出版地址：http：／／w ww．cnki．net／kcms／detail／11．2422．TN．20141105．1633．016．html

國家自然科學基金（61372167）資助課題