單載波二維碼分與頻分多址系統及其性能分析

丁 丹，程乃平

（裝備學院光電裝備系，北京101416）

單載波二維碼分與頻分多址系統及其性能分析

丁 丹，程乃平

（裝備學院光電裝備系，北京101416）

提出一種單載波二維碼分與頻分多址（single carrier two dimensional code and frequency division multiple access，SC-2DCFDMA）系統，借助時頻二維擴頻矩陣解決普通單載波碼分與頻分多址（single carrier code and frequency division multiple access，SC-CFDMA）系統中擴頻因子與子帶寬度之間的矛盾；構建了SC-2DCFDMA系統發送端與接收端的數學模型；分析了其在加性高斯白噪聲信道和頻率選擇性信道下的理論誤碼率。仿真結果表明，理論與仿真誤碼率曲線吻合；在相同的擴頻因子條件下，SC-2DCFDMA系統具有比SC-CFDMA系統更窄的用戶子帶寬度和更優的誤碼率性能；在多用戶場景下，雖然信道的頻率選擇性會造成頻域擴頻碼的正交性損失，但這種損失可由時域擴頻碼的正交性來彌補，從而使得SC-2DCFDMA系統的多用戶性能優于SC-CFDMA系統。

單載波頻分多址；二維擴頻；誤碼率；擴頻因子

0 引 言

單載波碼分與頻分多址（single carrier code and frequency division multiple access，SC-CFDMA）技術［1-4］是單載波頻分多址（single carrier frequency division multiple access，SC-FDMA）［5-7］技術與碼分多址（code division multiple access，CDMA）技術相結合的產物，也稱為單載波頻分多址與碼分多址（single carrier frequency division multiple access and code division multiple access，SC-FDMA-CDMA）技術。它在SC-FDMA發送之前先對數據進行頻域擴頻處理，這樣不僅能增強抗干擾能力，而且也可擴展用戶容量。

然而，在SC-CFDMA系統中，用戶的擴頻因子受限于其所占用的子載波數M；若一味地增大M則會導致用戶子帶寬度擴展，這樣一方面會引入更多的信道噪聲與干擾；另一方面，如果子帶寬度超過信道的相干帶寬，還會破壞擴頻碼的相關性［8］。所以，為了解決子帶寬度和擴頻因子之間的矛盾，提出一種基于二維擴頻思想的單載波二維碼分與頻分多址（single carrier two dimensional code and frequency division multiple access，SC-2DCFDMA）系統。它采用時域擴頻與頻域擴頻串聯的方法構建時頻二維擴頻矩陣，在不增加用戶子載波數M的前提下增加擴頻因子。與普通SC-CFDMA相比，在相同的用戶子帶寬度下，SC-2DCFDMA具有更大的擴頻因子；與基于正交頻分復用（orthogonal frequency division multiplexing，OFDM）［9-11］的傳統二維擴頻［12］相比，SC-2DCFDMA又具有較低的峰均比（peak to average power ratio，PAPR）［13］。因為SC-2DCFDMA是在SC-FDMA傳輸前進行時頻二維擴頻，所以SC-2DCFDMA有著與SC-FDMA相同的PAPR，在無成形濾波的四相相移鍵控（quadrature phase shift keyhg，QPSK）調制方式下，若采用集中式子載波分配［1］，其PAPR將比傳統二維擴頻低約3 dB；若采用交織式子載波分配［1］，優勢則擴大至10 dB左右［14］。

1 系統模型

1.1 發送端

SC-2DCFDMA系統發送端模型如圖1（a）所示。第u個用戶的第m個符號先被長為L的時域擴頻向量b（u）＝擴頻，然后根據所占用的子載波數M進行并行復制并且分配到M條子載波上，進而被大小為M×L的頻域擴頻矩陣為其第k列向量）擴頻。時頻二維擴頻矩陣可表示為式（1），其中C（u）各列可相同或相異，本節先令各列相同，后面再分析各列相異的情況。

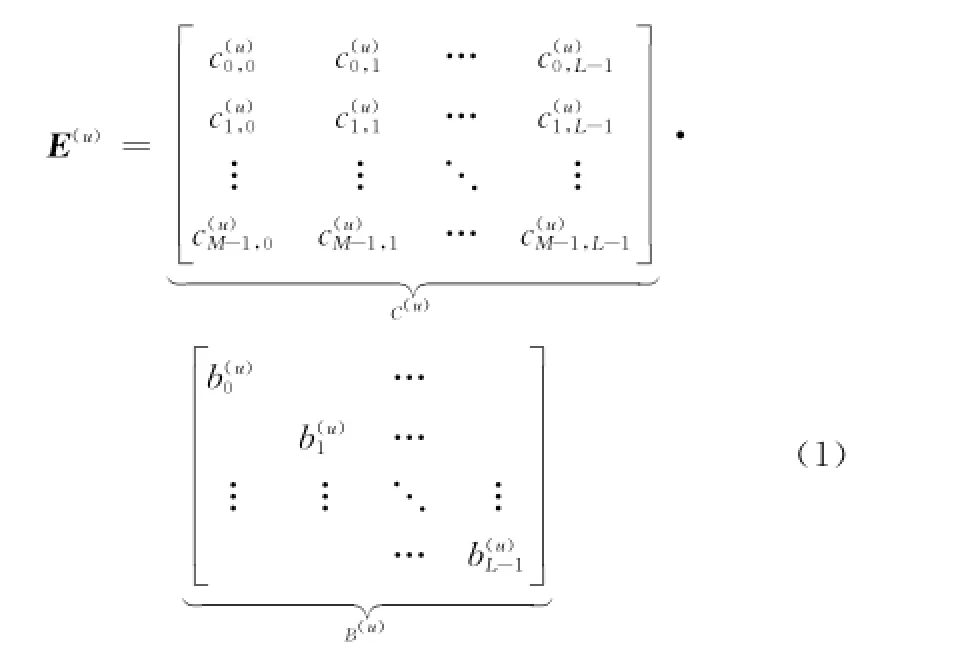
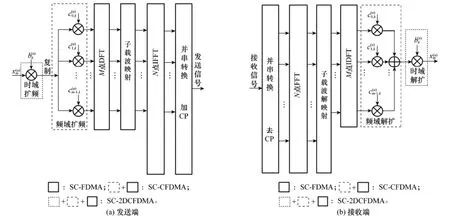
圖1 SC-2DCFDMA系統模型

二維擴頻后進行M點離散傅里葉變換（discrete Fourier transform，DFT）、子載波映射、N點IFFT變換和功率歸一化調整，得到的信號如式（2）所示，再插入循環前綴（cyclic prefix，CP），即可得到SC-2DCFDMA發送信號。

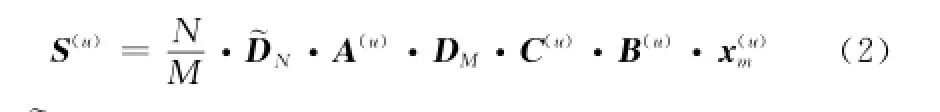
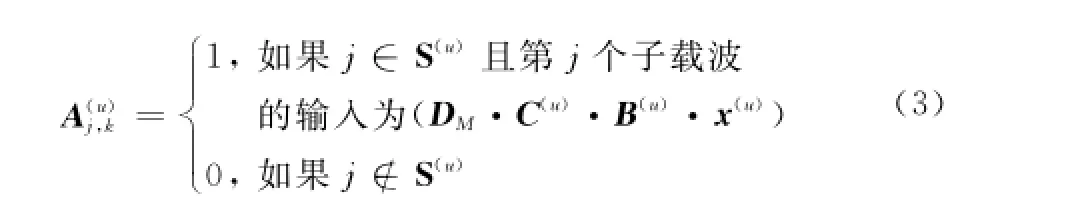
1.2 接收端

接收端模型如圖1（b）所示，經信道傳輸后，在同步正確的前提下，經過去CP、FFT后得

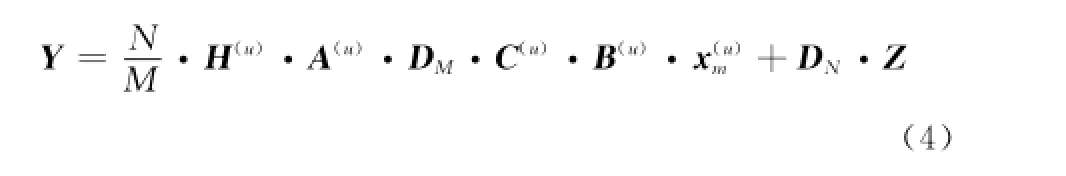
式中，Z是由單邊功率譜密度為σ2＝N0的復高斯白噪聲組成的M×L維矩陣；H（u）為用戶u的信道矩陣，是N×N階的對角陣，其對角線元素為

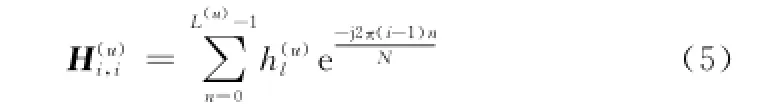
式中，L（u）為用戶u經歷的信道時延擴展為用戶u的信道單位脈沖響應系數。令為用戶u的解映射矩陣，那么接收端用戶u的M點逆DFT（inverse DFT，IDFT）運算輸出矩陣為

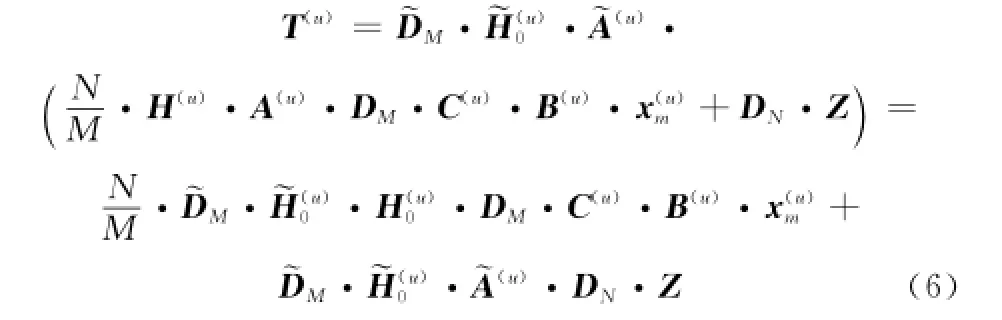
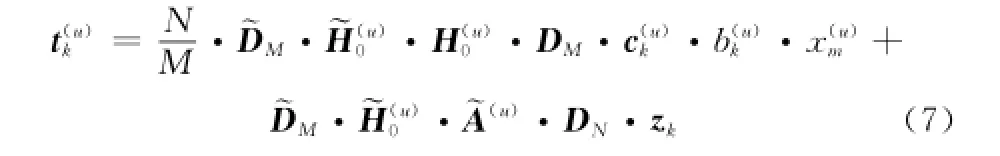
式中，zk為對Z的第k列取實部得到的列向量。對進行頻域解擴的結果為

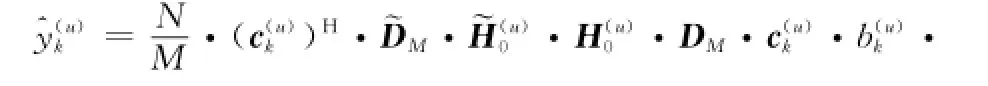
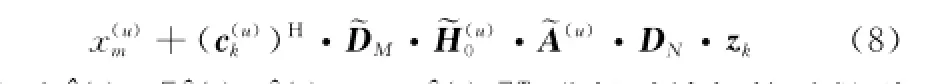
2 誤碼率分析

在頻率選擇性信道下，若采用最小均方誤差（minimum mean square error，MMSE）均衡［5，13］，令γ為信噪比，則均衡矩陣為

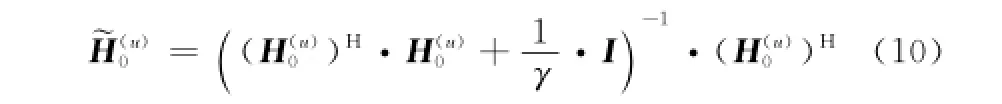
代入式（8）得頻域解擴后的信號為

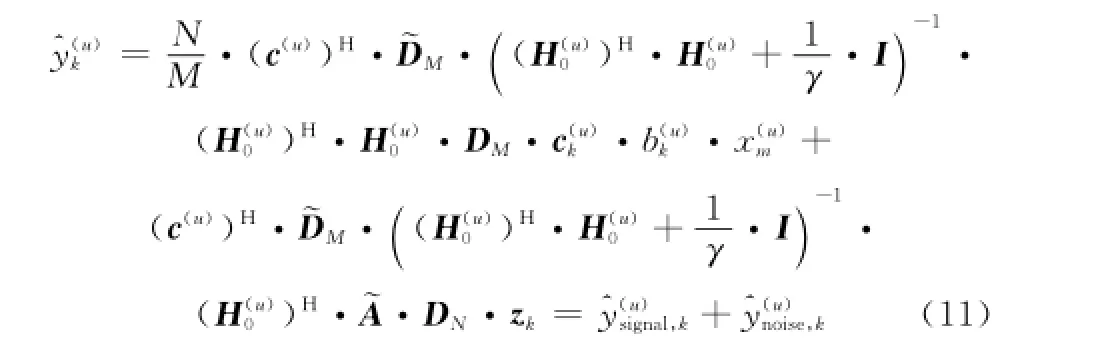
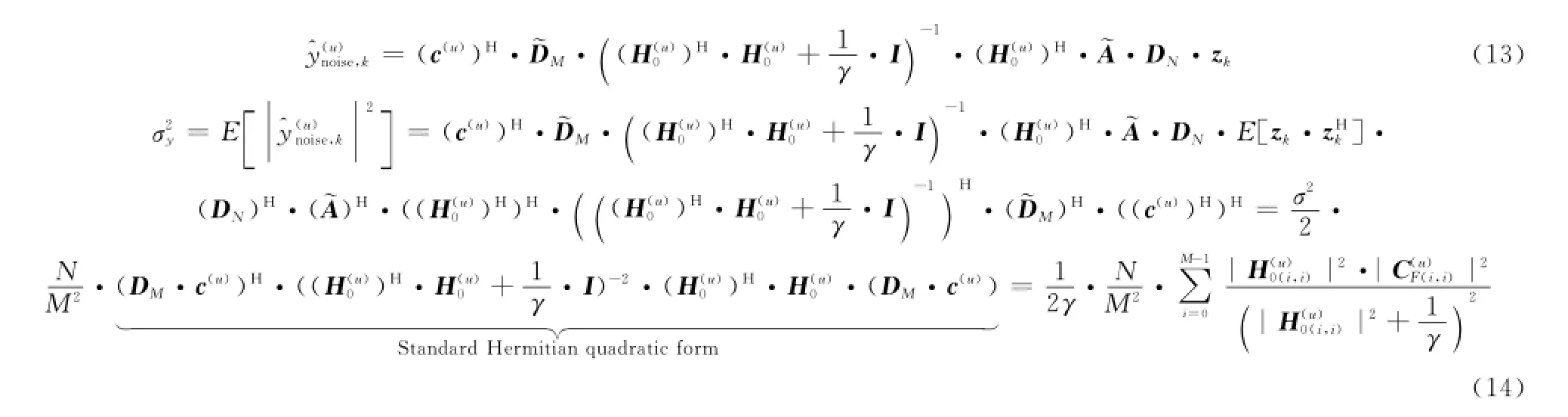
因此，頻域解擴后的信號向量可建模為

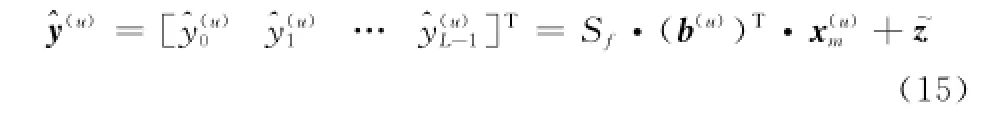
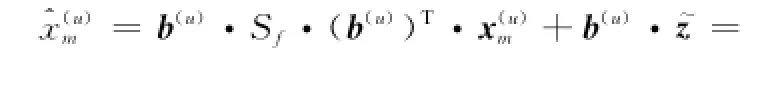
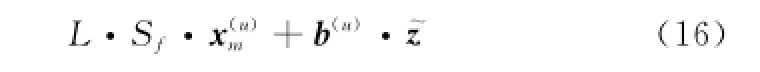
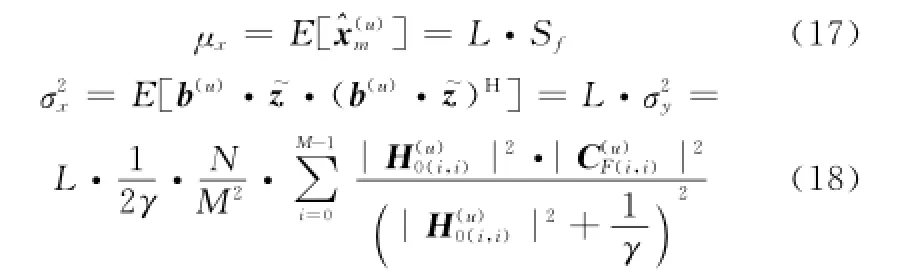
則理論誤碼率為

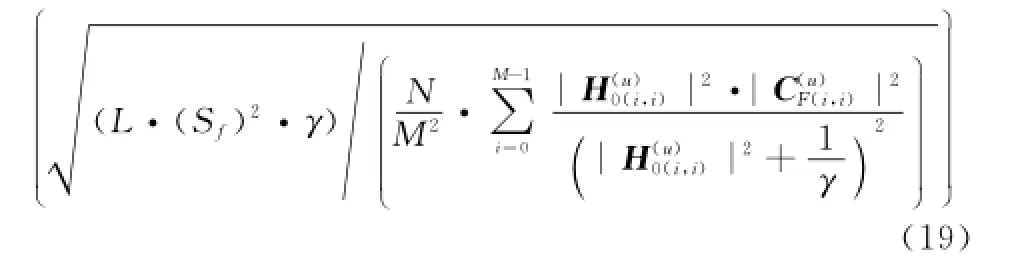
同理可得SC-2DCFDMA系統在頻率選擇性信道下采用迫零（zero forcing，ZF）［5，13］均衡以及在加性高斯白噪聲信道下的理論誤碼率，如表1所示，注意SC-CFDMA實為SC-2DCFDMA在L＝1時的特例。由表1可知，在不超過信道相干時間的前提下，增加L可降低系統誤碼率。

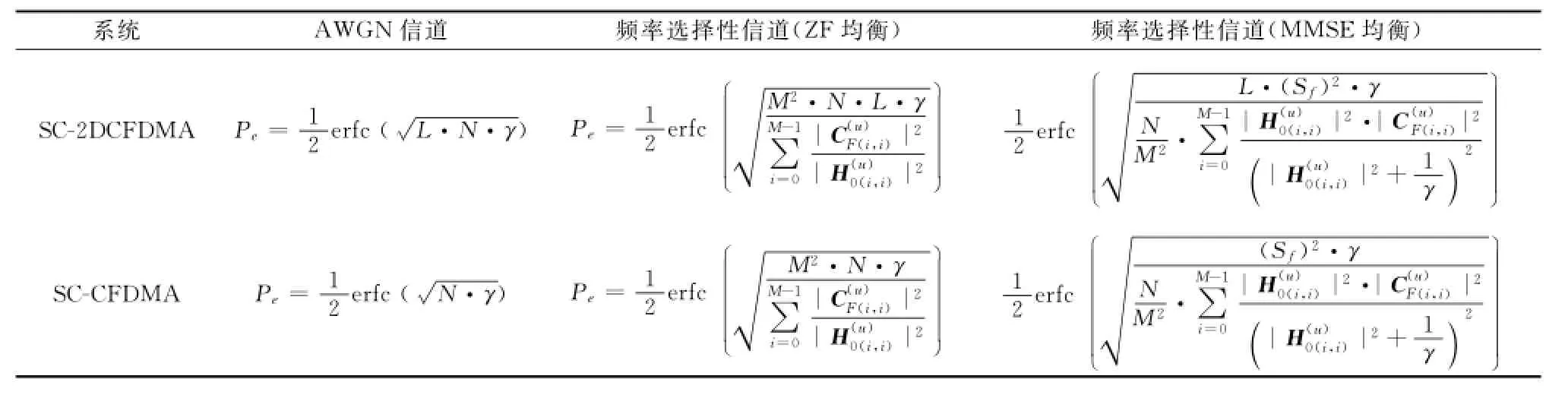
______系統 AWGN信道 頻率選擇性信道（ZF均衡） 頻率選擇性信道（MMSE均衡）M2·N·L·γ SC-2DCFDMA Pe＝12erfc（L·N·■γ） Pe＝12erfc■■■M－1___ F（i，i）｜2｜H（u）0（i，i）｜∑｜C（u）i＝0 2■■L·（Sf）2·γ■■｜H（u）M－1 2 12erfc 0（i，i）｜2·｜C（u）F（i，i）｜NM■2·∑2 i＝0（｜H（u）0（i，i）｜2＋1 γ）■■■■（Sf）2·γ M－1 2 SC-CFDMA Pe＝γ） Pe＝12erfc 12erfc（N·■M－1 M2·N·γ 12erfc ｜H（u）｜C（u）F（i，i）｜2 0（i，i）｜2·｜C（u）F（i，i）｜■■■NM∑■2·∑2 i＝0｜H（u）0（i，i）｜2■■i＝0 ___（｜H（u）0（i，i）｜2＋1 γ）■■_

3 仿真分析

利用Matlab軟件對SC-2DCFDMA的系統性能進行仿真。單用戶情況下的仿真條件為：

信道類型：加性高斯白噪聲信道、國際電聯步行A信道［16］、航空衛星移動通信信道［17］；

均衡算法：MMSE、ZF；

擴頻碼：時域Walsh碼、頻域Gold碼；

FFT點數N：512；

子載波映射：交織式；

多普勒：無；

子信道帶寬：30 KHz（擴頻因子M×L＝64×2）15 KHz（擴頻因子M×L＝128×1）；

系統采樣率：7．68 MHz；

用戶號u：2。

仿真結果如圖2所示。可以看出，無論采用何種信道類型、擴頻因子組合與均衡算法（加性高斯白噪聲信道下無均衡），首先，SC-2DCFDMA系統的理論與仿真誤碼率曲線吻合；其次，在相同的總擴頻因子（128）下，SC-2DCFDMA的誤碼率性能明顯優于SC-CFDMA，這是因為二維擴頻的處理方法壓縮了用戶子帶寬度，降低了噪聲；此外，MMSE均衡算法的性能優于ZF均衡，因為MMSE算法改善了ZF算法對噪聲的放大作用。

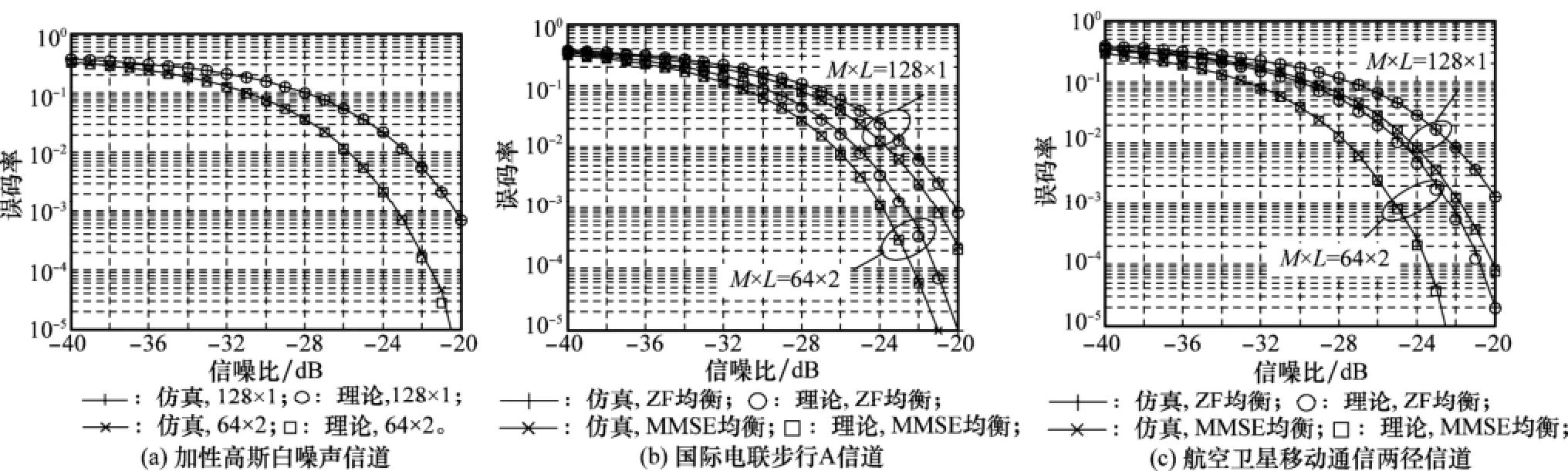
圖2 單用戶SC-2DCFDMA系統誤碼率性能仿真

在多用戶場合下，由于網絡覆蓋范圍廣、用戶地理位置分散，各用戶經歷著不同的信道響應。比如航空衛星移動通信的兩徑信道，不同的地面反射系數、不同的飛行高度分別會造成反射路徑的幅度和時延不同。這種情況下的多用戶SC-2DCFDMA系統誤碼率性能仿真結果如圖3所示。擴頻因子組合M×L選擇32×8；用戶數為8，占用同一子載波集；信道類型選擇航空衛星移動通信的兩徑信道，各用戶反射路徑的幅度和時延不相等；其余仿真條件與單用戶情況相同。由圖3可看出，若僅靠頻域擴頻碼來區分多用戶，誤碼率性能會有明顯惡化，這是因為對某個用戶的頻域均衡會改變其他用戶頻域碼的結構，進而破壞用戶間的正交性、引入多用戶干擾（multi-user interference，MUI）；而若能再依靠時域擴頻碼來區分多用戶，則無論各用戶頻域碼是否相同，各時刻k∈［0，L－1］頻域解擴引入的MUI相等，所以各用戶時域碼的正交性完好，能夠消除 MUI。也就是說，頻域碼的正交性損失可由時域碼的正交性來彌補。但也不能一味依靠時域擴頻碼來區分多用戶，因為隨著用戶數的增多，要求時域碼的長度也隨之加長，如果超過信道的相干時間，就會在時域解擴環節引入M UI。

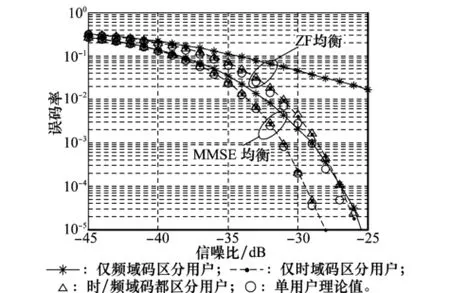
圖3 多用戶SC-2DCFDMA系統誤碼率性能仿真

另外還有一種特殊情況，即頻域擴頻矩陣C（u）各列互不相同，這時信號的保密性強于各列相同的時候；但在多用戶場合下，各時刻k∈［0，L－1］頻域解擴引入的MUI不相等，會破壞各用戶時域擴頻碼之間的正交性，從而在時域解擴的過程中引入MUI，仿真結果如圖4所示。注意即便是單用戶條件下，誤碼率的仿真值也劣于理論值，這是因為式（12）中的C（u）F（i，i）在每一時刻k∈［0，L－1］不再保持恒定不變，導致后續推導過程中實際值與理論值之間存在誤差。

圖4 頻域擴頻矩陣C（u）各列不同時的誤碼率性能仿真

最后，對SC-2DCFDMA系統抗窄帶干擾的性能進行仿真。仿真條件為：

信道類型：加性高斯白噪聲信道；

信噪比：－15 dB；

干擾信號：8個單頻窄帶干擾，分別處于第2／18／34／50／66／82／98／114個子載波的位置，使得在不同擴頻因子組合下，均有8個子載波分別受到單頻窄帶干擾；

其余仿真條件：與單用戶情況相同。

圖5為仿真結果。可以看出，SC-2DCFDMA抗窄帶干擾的能力強于SC-CFDMA。這是因為在二維擴頻模式下，每個子載波都具有一定的時域擴頻增益，能夠在時域解擴環節對窄帶干擾起到抑制作用。

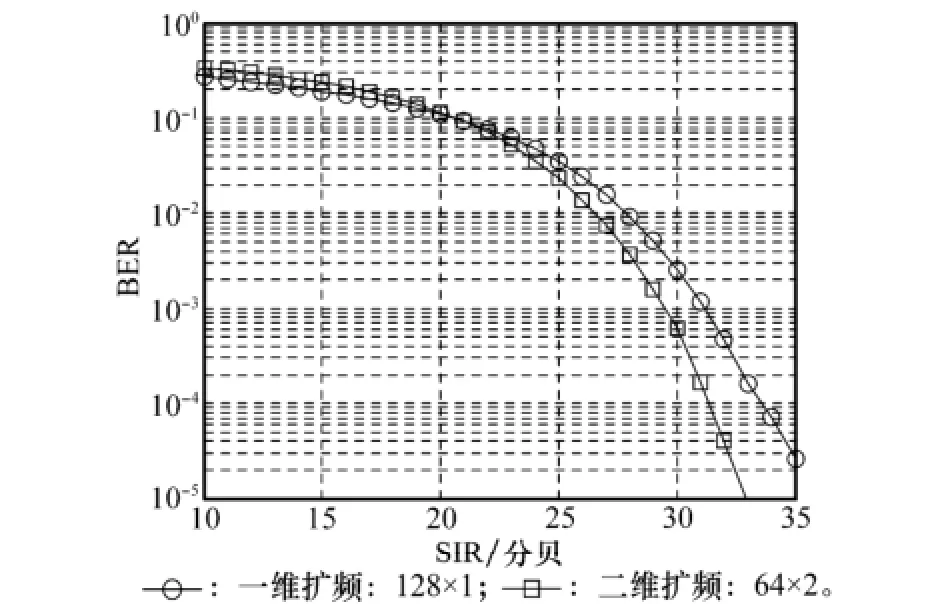
圖5 窄帶干擾條件下的誤碼率性能仿真

4 結 論

本文提出了一種基于時頻二維擴頻思想的SC-2DCFDMA系統；分別推導了其在加性高斯白噪聲信道以及頻率選擇性信道中的誤碼率解析式。計算機仿真結果顯示：單用戶SC-2DCFDMA系統的仿真與理論誤碼率曲線吻合；且在相同的擴頻增益條件下，SC-2DCFDMA具有較小的用戶子帶寬度和較優的誤碼率性能。在多用戶場合中，信道的頻率選擇性會破壞用戶頻域擴頻碼之間的正交性，但這種正交性的損失可由時域擴頻碼的正交性來彌補。這也體現了SC-2DCFDMA相對于SC-CFDMA的優越性。另外，頻域擴頻矩陣的結構對SC-2DCFDMA的性能也有不可忽視的影響。相對于各列相異的結構，采用各列相同的結構雖然降低了信號的保密性，但卻不會破壞時域擴頻碼的正交性，使得無論是單用戶還是多用戶的誤碼率性能相對更優。SC-2DCFDMA是一項較有潛力的技術，后續還將對SC-2DCFDMA的信道估計技術、檢測技術和時頻同步技術做進一步研究。

［1］Myung H G，Goodman D J．Single carrier FDMA，a new air interface for long term evolution［M］．New York：John Wiley＆Sons，Ltd，2008：55- 56．

［2］Myung H G．Hybrid subcarrier mapping method and system［P］．United States．US 2013／0010703 A1，2013．

［3］Paul A，Jose I．UWB modulation scheme“SC-CFDMA”formulti-user communications［C］∥Proc.of 11th Institute of Research and Journals International Conference，2014：34- 37．

［4］Luo Z Q，Xiong X Z．Performance comparison of SC-CFDMA and OFDM-CDMA systems for uplink［C］∥Proc.of the IEEE International Conference on Consumer Electronics，Communications and Networks，2011：1475- 1479．

［5］Wen M W，Cheng X，Wang M，et al．Error probability analysis of interleaved SC-FDMA systems over Nakagamim frequency-selective fading channels［J］．IEEE Trans.on Vehicular Technology，2013，62（2）：748- 761．

［6］Wu P R，Robert S，Vijay K B．Optimal power allocation for wideband cognitive radio networks employing SC-FDMA［J］．IEEE Communications Letters，2013，17（4）：669- 672．

［7］Dechene D J，Shami A．Energy-aware resource allocation strategies for LTE uplink with synchronous HARQ constraints［J］．IEEE Trans.on Mobile Computing，2014，13（2）：422- 433．

［8］Hanzo L，Keller T．OFDM and MC-CDMA，a primer［M］．New York：John Wiley＆Sons，Ltd，2006：239．

［9］Zhang Z F，Wu A A，Yang J，et al．Joint cooperative complex field network coding and OFDM technology algorithm［J］．Systems Engineering and Electronics，2013，35（10）：2198- 2203．（張祖凡，吳愛愛，楊靜，等．聯合OFDM技術的協作復數域網格編碼算法［J］．系統工程與電子技術，2013，35（10）：2198- 2203．）

［10］Cui J，Zhang B，Zhang Y Z．Channel estimation method used in UAV PRP-OFDM data links［J］．Systems Engineering and Electronics，2013，35（11）：2400- 2404．（崔金，張波，張彥仲．一種用于無人機的PRP-OFDM數據鏈路信道估計方法［J］．系統工程與電子技術，2013，35（11）：2400- 2404．）

［11］Saengudomlert P．On the benefits of pre-equalization for ACO-OFDM and flip-OFDM indoor wireless optical transmissions over dispersive channels［J］．Journal of Lightwave Technology，2014，32（1）：70- 80．

［12］Zhou J，Tang Y X，Xie S L，et al．Performance of time-frequency two dimensional spread spectrum system in multi-tone jamming environment［J］．Journal of Electronics&Information Technology，2006，28（11）：2107- 2110．（周鍵，唐友喜，謝勝琳，等．多音干擾環境中時頻二維擴頻系統的性能［J］．電子與信息學報，2006，28（11）：2107- 2110．）

［13］Zhang S，Yang L，Li SQ．Algorithm combined PSO and phase factor optimal pair for PAPR reduction in OFDM systems［J］．Systems Engineering and Electronics，2012，34（7）：1479-1483．（張帥，楊霖，李少謙．PSO與相位因子優選對結合降低OFDM峰均比的算法［J］．系統工程與電子技術，2012，34（7）：1479- 1483．）

［14］Ebrahimi H．Adaptive SC-FDMA with pulse shaping for wireless cognitive radio［C］∥Proc.of the International Symposium on Communications and Information Technologies，2012：519- 523．

［15］Basnayaka D A，Smith P J，Martin，P A．Performance analysis of macro diversity MIMO systems with MMSE and ZF receivers in flat Raleigh fading［J］．IEEE Trans.on Wireless Communications，2013，12（5）：2240- 2251．

［16］3GPP TS 25．104．Base Station（BS）radio transmission and reception（FDD）specification［S］．New York：The 3rd Generation Partnership Project，2012：93．

［17］Recommendation ITU-R P．682-3．Propagation data required for the design of earth-space aeronautical mobile telecommunication systems［S］．Geneva：International Telecommunication Union，2012．

Single carrier two dimensional code and frequency division multiple access system and its performance analysis

DING Dan，CHENG Nai-ping
（Department of Optical and Electronic Equipment，Academy of Equipment，Beijing 101416，China）

A single carrier two dimensional code and frequency division multiple access（SC-2DCFDMA）system is proposed．The contradiction between spreading factor and subband width in common single carrier code and frequency division multiple access（SC-CFDMA）system is resolved by the use of time-frequency two dimensional spreading matrix．The mathematical models of SC-2DCFDMA transmitter and receiver are constructed．The analytical bit error rate（BER）under additive white Gaussian noise channel and frequency selective channel are analyzed．Simulation results show that the analytical and simulated BER curves coincide with each other．With equal spreading factor，SC-2DCFDMA system has narrower user subband and superior BER performance．In a multi-user scenario，although channel frequency selectivity induces the orthogonality loss of the frequency domain spreading code，this kind of loss could be compensated by the orthogonality of time domain spreading code．Thus multi-user performance of SC-2DCFDMA system is better than SC-CFDMA system．

single carrier frequency division multiple access（SC-FDMA）；two dimensional spread spectrum；bit error rate（BER）；spreading factor

TN 914．4

A

10．3969／j．issn．1001-506X．2015．04．31

丁 丹（1980-），男，講師，博士研究生，主要研究方向為通信系統設計。E-mail：ddnjr＠163．com

1001-506X（2015）04-0923-06

2014- 05- 20；

2014- 08- 31；網絡優先出版日期：2014- 10- 21。

網絡優先出版地址：http：／／w ww．cnki．net／kcms／detail／11．2422．TN．20141021．1102．002．html

“十二五”裝備預研項目；國家級項目資助課題

程乃平（1963-），男，教授，博士，主要研究方向為通信系統設計。E-mail：Cheng_np＠163．com