模糊C均值聚類區間型模糊化參數模型

肖滿生，肖 哲，文志強，于惠鈞

（1．湖南工業大學科技學院，湖南株洲412008；2．湖南工業大學計算機與通信學院，湖南株洲412008）

模糊C均值聚類區間型模糊化參數模型

肖滿生1，2，肖 哲1，文志強2，于惠鈞1

（1．湖南工業大學科技學院，湖南株洲412008；2．湖南工業大學計算機與通信學院，湖南株洲412008）

針對經典模糊C均值聚類算法中模糊加權指數對聚類的影響及其取值范圍不確定性問題，提出了一種區間型模糊加權指數的設計模型。分析該模型設計的理論依據及對聚類結果的影響，推導出包括模糊隸屬度劃分矩陣、模糊聚類中心等基于該模型的模糊化參數表示方法。理論分析和實驗證明，區間型模糊化參數模型的設計在基于模糊劃分的數據處理中取得了很好的效果。

模糊C均值；區間型模糊加權指數；模糊化參數；不確定性

0 引 言

經典的模糊C均值（fuzzy C-means，FCM）聚類是一個基于目標函數的帶約束的非線性規劃過程，通過對參數的優化求解獲得樣本集的模糊劃分或聚類，該方法及其改進技術在信息技術和控制決策等領域獲得了廣泛的應用，如圖像處理［12］、模式識別［3］、數據挖掘［4］、模糊決策［5］等。

然而，隨著研究深入，經典的FCM聚類算法在實際應用過程中還要受到諸多限制，相關理論也有待進一步完善。如在處理不確定性問題時，經典的FCM算法對樣本的劃分有明確的隸屬度約束，這類算法叫1型FCM（1-TFCM）［6］；而客觀世界在對樣本進行分析和模式識別時存在各種各樣的不確定性，因此，如果合理地給出樣本隸屬度的模糊程度，即樣本的模糊隸屬度，則更能恰當地描述集合的模糊性，這種改進的FCM算法叫2型FCM算法（2-TFCM），在這方面，文獻［6- 9］取得了一定的研究成果。另外，在研究圍［1．1，5］以后，文獻［11- 14］進行了大量研究。文獻［11］從聚類有效性實驗中得到m的最佳區間為［1．5，2．5］；文獻［12］基于模糊決策提出了一種m值的優選方法；文獻［13］通過在標準FCM的隸屬度μik的約束條件中引入冪指數r，提出一種雙指數模糊C均值算法（double index fuzzy C-mean，DI-FCM），該算法在理論上有效地擴展了m的取值范圍；文獻［14］從粒子群優化的角度，得到了一個模糊加權指數值，并由此解釋了FCM聚類對初始聚類中心敏感的問題。這些方法對模糊加權指數m的確定都是憑經驗或實驗進行，缺乏理論依據和有效的評價方法。另外，文獻［9］通過α-平面截集描述模糊集，可以得到m值的設計與具體聚類樣本集有關，但其精確選取是非常困難也是不可能的。

基于此，本文在分析現有的FCM聚類及其改進算法的模糊化參數過程中，模糊加權指數m是FCM聚類算法中重要參數，其直接影響到聚類結果的不確定性程度。在實際應用過程中，自文獻［10］引入并給出m經驗值范基礎上，受文獻［15- 17］中改進的FCM聚類特點和模糊化參數設計啟發，包括模糊隸屬度函數的設計與評價、模糊聚類中心及聚類數目的確定、樣本與聚類中心的距離計算等，提出了一種區間型FCM聚類模糊化參數設計模型。即首先通過分析模糊加權指數的不確定性及其對聚類的影響，提出了區間型模糊加權指數m的設計方法，基于區間型模糊加權指數，推導出模糊隸屬度、模糊聚類中心（質心）的設計方法，通過“反模糊化”后得到確定的模糊化參數，并將該方法應用于圖像分割、模式識別等實驗。理論分析和實驗對比表明，本文提出的FCM模糊化參數模型不但改善了FCM算法的聚類性能，提高了樣本劃分的效率，而且對模糊聚類算法的進一步研究和拓展有很好的指導意義。

1 模糊加權指數的不確定性分析與設計

FCM聚類目標函數為

該目標函數中，模糊加權指數m控制著樣本在類間的分享程度。理論分析和實際應用表明，隨著m的增加，聚類的目標函數值單調下降，這與最小化目標函數的思想一致，而且較大的m還有平滑聚類結果、抑制噪聲的功能，但是，參數m還控制著FCM聚類結果的模糊性，m越大，聚類結果越模糊，模糊邊界越大，從這個角度來說，又希望m取值不要太大。因此，合理的m值應該取多少，一直是FCM聚類中備受關注的問題。

m取值的不確定性及對聚類結果的影響可用圖1、圖2表示。

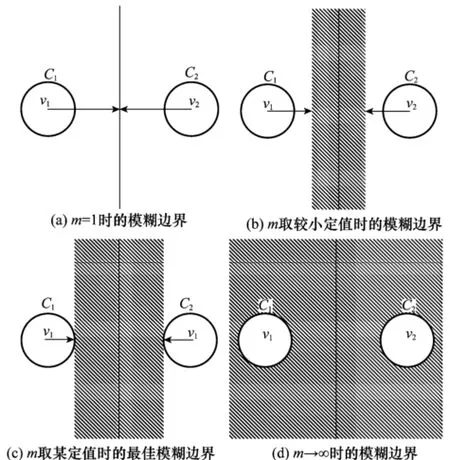
圖1 劃分類容量相近時參數m對模糊聚類的影響

圖1 中，C1、C2是兩劃分類，v1、v2分別為兩劃分類的聚類中心，兩劃分類之間的垂直平分豎線（陰影區域）為其模糊邊界，也叫決策邊界，位于邊界左側（右側）的樣本歸屬于類C1（C2），而位于邊界上的數據樣本則對于類C1（C2）有相同的隸屬度，其所歸屬某類的程度非常模糊。圖1中，對于容量相近的兩劃分類，當m＝1時，其模糊邊界是一條直線，由于邊界區域很窄，當受到噪聲等不確定因素影響時，邊界（豎線）附近的樣本很容易產生錯誤劃分的情況，如圖1（a）所示；隨著取值的增大，模糊邊界將變寬，如圖1（b）中的陰影部分所示，邊界的擴展可將更多不確定的數據點納入模糊邊界中，使其具有相同的隸屬度，以便減小聚類中心更新時不確定因素的影響；當m進一步擴大，使模糊邊界擴展到圖1（c）所示的位置時，此時的邊界區域最為理想，劃分結果最為明晰，此時除了劃分類C1、C2之間的樣本（全位于邊界區域）外，其余樣本都有明晰的歸屬類；然后，當m進一步擴大，以致m→∞時，模糊邊界充滿全域，如圖1（d）所示，此時模糊化程度達到最大，所有樣本的隸屬度（c為劃分類數目），因而FCM算法失去了劃分特性。

圖2 劃分類容量不同時參數m對模糊聚類的影響

上述是兩劃分類容量相等或相近的情況，對于劃分類容量不同的樣本，當m取某一定值時，模糊邊界如圖2（a）所示，這時，本來屬于劃分類C2中的樣本卻歸屬到模糊邊界，而左邊模糊邊界之外的本不歸屬于劃分類C1的樣本則被劃到類C1中，這樣的模糊邊界不理想，模糊聚類的不確定性高，如果能針對不同的劃分類容量設計不同的參數m，使模糊邊界達到一個理想區域，如圖2（b）所示，這時，在保證每個聚類中心v1、v2與豎線的距離（位置）不變的情況下，所有樣本數據都有較理想的隸屬度，即除了模糊邊界（兩劃分類之間）的樣本外，其余樣本都能較好地歸屬于相應的類，這種情況下，模糊聚類的準確性有很大的提高。

針對上述模糊加權指數m取值的不確定性及對不同容量的劃分類的模糊聚類影響，將模糊加權指數區間化，即設計一模糊區間：m＝［m1，m2］，其中m1、m2分別對應于較小、較大容量差異的劃分類，這樣，當劃分類容量不同時的樣本進行聚類分析時，根據最大、最小劃分類設計的區間模糊加權指數求取樣本的隸屬度，并確定聚類中心，這樣能顯著改善聚類性能，同時也降低了模糊加權指數設計的不確定性。

2 FCM聚類模糊化參數模型

本節根據第1節所提出的區間型模糊加權指數，設計并推導FCM聚類中其他模糊化參數模型，并通過“反模糊化”得到具體的聚類參數，包括模糊隸屬度、模糊聚類中心等。

2.1 區間型模糊隸屬度及聚類中心計算模型

隸屬度是FCM聚類中的重要參數，它直接反映某一樣本隸屬于某一劃分類的程度，在第1節中，當模糊加權指數被設計為區間型參數后，相應的模糊隸屬度也可以設計為區間型參數，即為形式，其中表示樣本xi對于劃分類j的最小隸屬度；ˉμj（xi）為最大隸屬度。以圖2中的v1和v2連線之間的一維樣本為例，設v1＝0，v2＝1，則樣本集X∈［0，1］，取模糊加權指數m1＝2.0，m2＝4，則基于區間型指數［m1，m2］的樣本集X對于劃分類C1的隸屬度表示形式如圖3所示。

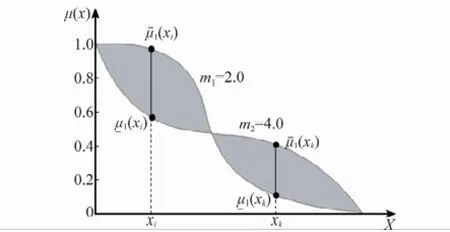
圖3 模糊隸屬度的區間型表示方法

圖3 中參數m1和m2所對應的隸屬度曲線所包含的陰影部分即為樣本的區間型隸屬度。參考經典FCM聚類的隸屬度計算方法，區間型隸屬度計算模型設計為

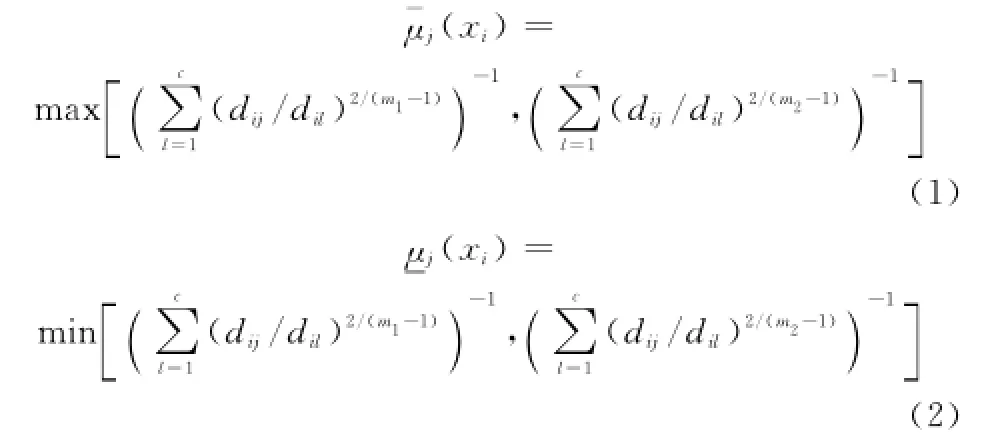
當用式（1）和式（2）來更新FCM聚類中心時，必然也將得到一個區間型聚類中心，設某一區間型聚類中心為，根據經典FCM聚類中心更新的推導方法，區間型聚類中心表示為

式中，J1，J2，…，Jn為樣本隸屬度區間，即分別為聚類中心的左邊界值和右邊界值（即最大值和最小值），模糊加權指數m根據式（1）和式（2）可以在m1、m2之間變換，至于怎樣推導并得到該公式可參考文獻［10］，此處不再贅述。

2.2 區間型參數的反模糊化處理

區間型模糊化參數的設計使得模糊聚類更能表達聚類的不確定性需求和人們對于事務判斷的意愿。然而，在實際應用過程中，卻遇到了很大的困難：一是區間型參數的存在使得聚類更為模糊，對一些需要明確劃分的類增加了其不確定性程度；二是基于區間型參數的模糊劃分，其計算復雜度增加，特別對于大量的高維（多屬性）樣本集，其計算的復雜度將線性增長。基于此，本文設計了區間型參數的反模糊化處理方法，使得模糊聚類既能很好表達聚類的不確定程度，又能方便計算，實現類別的客觀劃分，兩者得兼。

第2.1節中式（3）只是區間型聚類中心表示形式。在實際應用中，我們必須事先確定其左、右邊界值vLj和vRj，當和確定后，可以利用式（4）進行反模糊化，得到確定的聚類中心vj。

區間型聚類中心右邊界vRj確定算法如下：

設樣本集X包含n個樣本x1，x2，…，xn，每一個樣本由M維屬性組成，即xi＝（xi1，xi2，…，xiM），通過對所有樣本的M個屬性分別進行升序排序后計算，得到樣本集聚類中心的右邊界（即聚類中心的最大值），具體描述如下：

給定加權指數m一個任意區間，即m＝［m1，m2］；

FOR

所有樣本xi＝（xi1，xi2，…，xiM）；

END FOR

用式（5）和式（6）計算樣本集的M維聚類中心v′j＝（v′j1，v′j2，…，v′jM）；

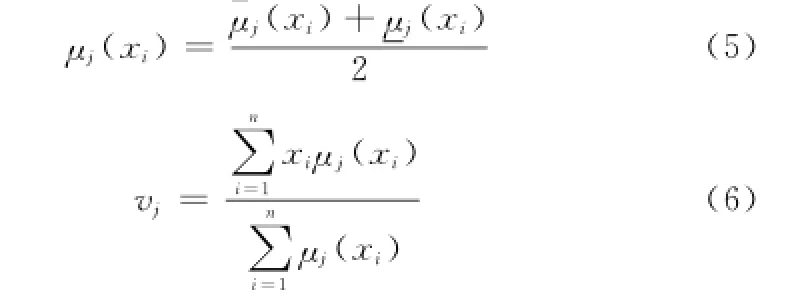
對n個樣本的M維特征，分別進行升序排序，即

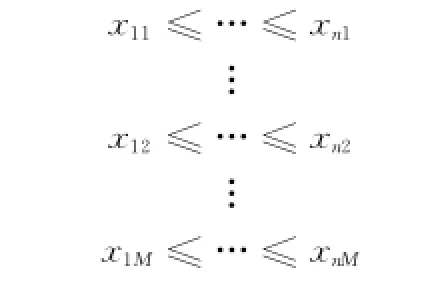
設一比較判斷變量com＝F；

FOR

所有樣本屬性

WHILE（com＝F）

查找一個索引值k（1≤k≤n－1），使得xkl＝v′jl＝x（k＋1）l（1≤l≤M）；FOR所有樣本

如果i≤k，則μj（xi）＝μj（xi），

END FOR

用更新的μj（xi）重新計算某一維聚類中心v′jh′（1≤l′≤M）；

如果v′jh＝＝v′jh′，則com＝T，否則設v′jh＝v′jh′

END WHILE

END FOR

最后，得到的v′jh為所求，即vRj＝（v′j1，v′j2，…，v′jM）。

上面算法得到了聚類中心的右邊界vRj，對于左邊界，只要對“FOR所有樣本”語句進行修改即可。

FOR所有樣本

END FOR

從上述算法中，確定樣本隸屬度函數，可以通過反模糊化來實現：假設在計算聚類中心vRj時的隸屬度函數為則樣本xi最終模糊化隸屬度可以設置為時為

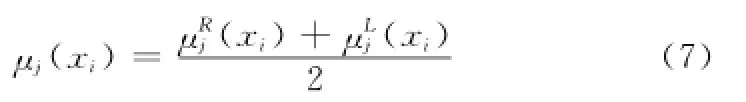
考慮到樣本xi是由M維屬性組成，因此和可由式（8）和式（9）來計算。

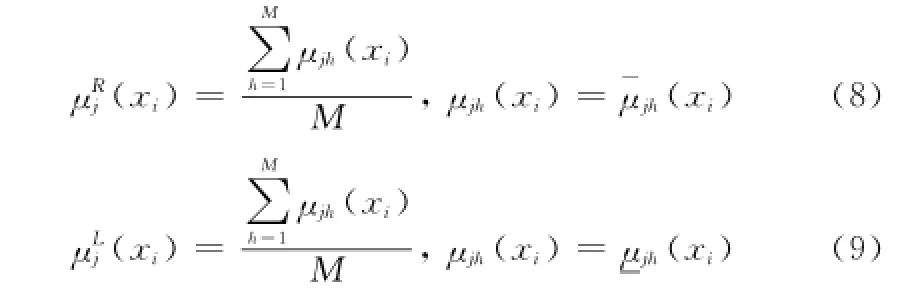
至于式（8）和式（9）中的μj（xi）的取值，采用的是還是可根據情況進行交換。

3 基于區間型模糊化參數的FCM聚類

有了第2節的模糊化參數定義，改進FCM聚類實現過程如下：

步驟1 給定聚類類別數c及區間型模糊加權指數［m1，m2］，n為數據集樣本總數，設定迭代停止閾值為ε，迭代次數計數器t＝0；

步驟2 初始化聚類中心v（l）；

步驟3 根據第2.1節中的式（1）和式（2）分別得到隸屬度區間的上下邊界值，即和

步驟5 利用第2.2節中提出的反模糊化公式（4），確定實際的模糊聚類中心v（t＋1）；

步驟6 如果‖v（t＋1）－v（t）‖＜ε，則停止迭代，輸出聚類中心v（t＋1），轉步驟7，否則t＝t＋1，根據新的v（t＋1），返回步驟3，繼續；

步驟7 根據步驟6得到的模糊聚類中心以及由此確定的區間型模糊隸屬度，對區間型模糊隸屬度進行反模糊化處理，即μ＝（μL＋μR）／2，得到最后的模糊劃分隸屬度矩陣，再按最大隸屬度原則得到聚類結果。

4 實驗結果分析

為了驗證本文提出區間型模糊化參數模型的有效性，引入了如下評價指標：

劃分系數vpc。基于模糊劃分矩陣的劃分系數表示為

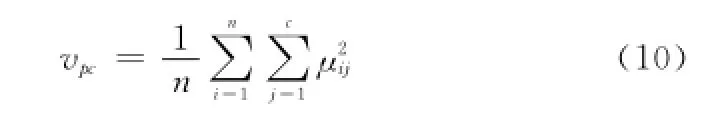
式中，n為樣本數量；c為聚類數；μij∈［0，1］為樣本xi相對于劃分類j的隸屬度，樣本的隸屬度越大，即μij越大，劃分系數越大，聚類效果越好。

劃分熵vpe。其表示為

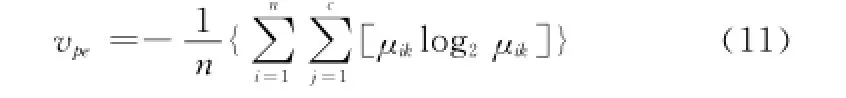
從式（11）中可看出，μik越大，則vpe值越小，故劃分熵越小，聚類效果越好。

劃分類內部均勻性測度（uniformity measure，UM）評判函數。該評判函數用來評價各劃分類內部樣本分布均勻的程度，其定義為

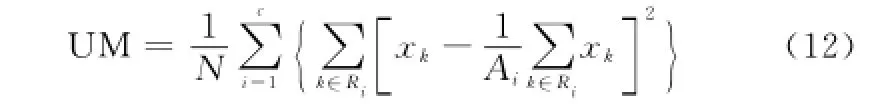
式中，Ri表示第i個劃分類（劃分區域）；Ai為該劃分類的樣本個數；N為歸一化系數，本文可設為樣本總數。從式（12）可分析出，劃分類內部樣本分布越均勻，即樣本xk與內部其他樣本相差越小，則UM值越小，因此，UM反映了各類樣本內部分布均勻性的程度。

實驗1 圖像分割實驗

圖4（a）為圖像處理中常用的圖像Camera man（128× 128），對其進行分割實驗。同時為了比較實驗效果，采用經典的FCM聚類算法與本文提出的基于區間型模糊化參數模型的FCM（interval-FCM，IFCM）方法進行對比分割。由于經典FCM算法本身無法自動獲取分類數目，因此采用讀入圖像灰度直方圖的方法獲取聚類數c及初始聚類中心v。經典FCM算法m＝2．0，IFCM算法選擇m1＝1．5，m2＝4．0。算法共進行了50次迭代。實驗環境：Visual C＋＋6．0編程，操作系統Windows 7，Dell Precision M4500，Intel Core i7 CPU，8G RAM。實驗將圖像按灰度不同分成人物、草地、天空3類。分割實驗結果如圖4（b）和圖4（c）所示，實驗中各評價參數對比如表1所示，其中time為實驗中計算耗時。

圖4 Cameraman圖像分割結果

表1 Cameraman圖像分割效果比較

從實驗中可以看出，對于評價指標vpe，IFCM＞FCM，對于評價指標vpe及UM，IFCM＜FCM，因此，本文提出的IFCM方法在圖像分割中其應用效果要比經典的FCM算法好。但本文提出的方法其計算的時間復雜度遠遠超過經典FCM算法。

實驗2 人造數據劃分

一個干凈無噪聲的人造實驗樣本數據集如圖5（a）所示，由一大兩小的3類樣本子集組成，采用高斯分布的隨機向量發生器產生，其主要參數如表2所示。另外，以此樣本集為基礎，在其中不斷增加均勻分布的噪聲點來進行實驗，每次增加30個，共進行11次，最后一次噪聲點數目達到300個。采用3種方法進行實驗：①經典FCM算法取m＝1．5；②經典FCM算法取m＝4．0；③本文方法IFCM取區間型m＝［2．0，5．0］。為了評價在加權指數m取不同值時，該樣本集中劃分類大小非均衡的聚類性能，各次實驗中采用均勻性測度值UM進行比較，實驗中UM比較曲線如圖6所示。

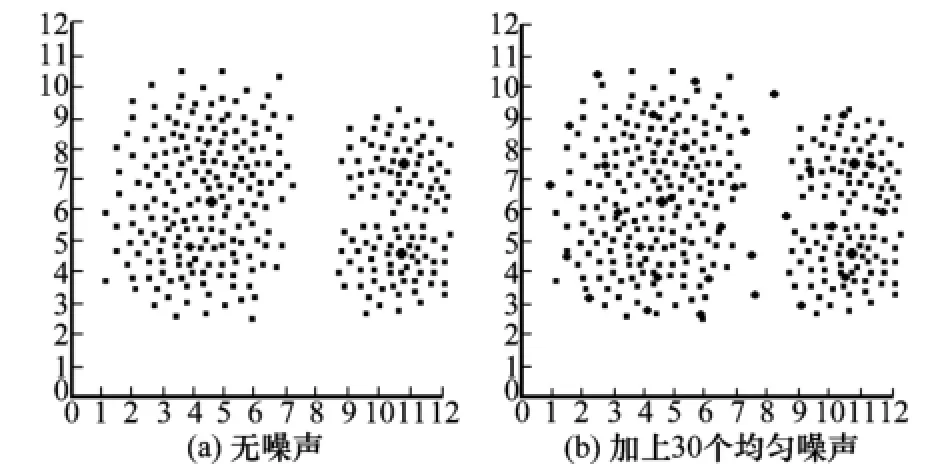
圖5 人造樣本數據集

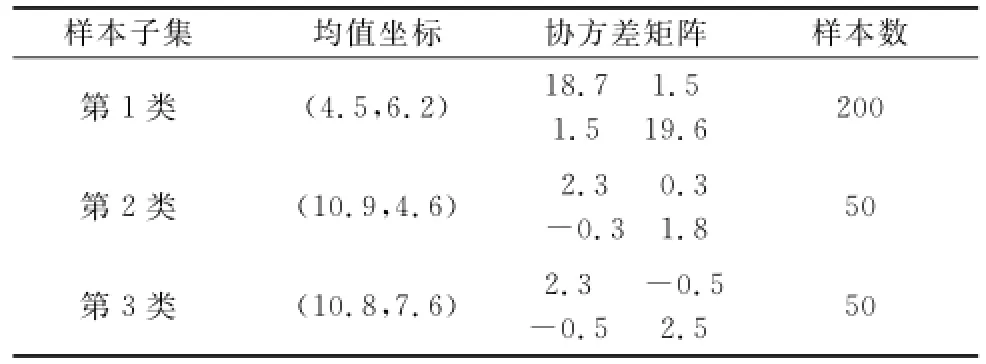
表2 無噪聲人造樣本集的主要參數

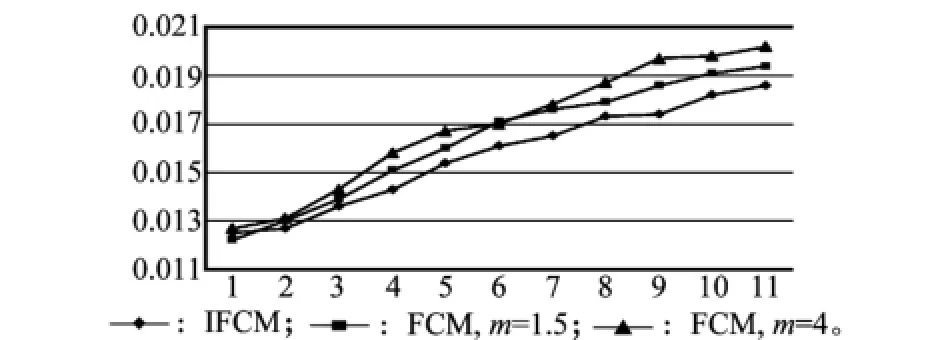
圖6 各次實驗中UM值比較

從圖5可以看出，在無噪聲干擾的情況下，各種方法劃分的效果都比較好，隨著噪聲增加，實驗中U M值不斷增加，表明實驗效果變差。另外，在各次實驗中，總體情況IFCM算法的UM值比其他兩種FCM測試方法所得到的UM值要小（除test case1中其UM值高于FCM m＝1．5的情況外），表明區間型模糊參數化方法的聚類效果要比經典FCM算法中模糊加權指數m取單一值的聚類效果好，特別是在模糊劃分類大小分布不均衡的情況下。

實驗3 IRIS數據分類實驗

本次實驗采用文獻［18］中提供的標準測試數據IRIS，它由四維空間的150個樣本組成，共有3個類（c＝3），每一個類50樣本，所有劃分類大小相等。對比實驗中，經典FCM算法模糊加權指數分別取m1＝1.5、m2＝2．5，IFCM方法中取m1＝2.0、m2＝4．0組成區間值［2．0，4．0］，實驗環境與實驗1中一致，實驗中聚類中心和隸屬度更新迭代次數為50次，實驗評價指標除了劃分系數vpc、模糊劃分熵vpe、均勻性測試度UM以及計算耗時time外，還增加了錯分樣本數（error）及錯分率（error ratio），實驗結果如表3所示。

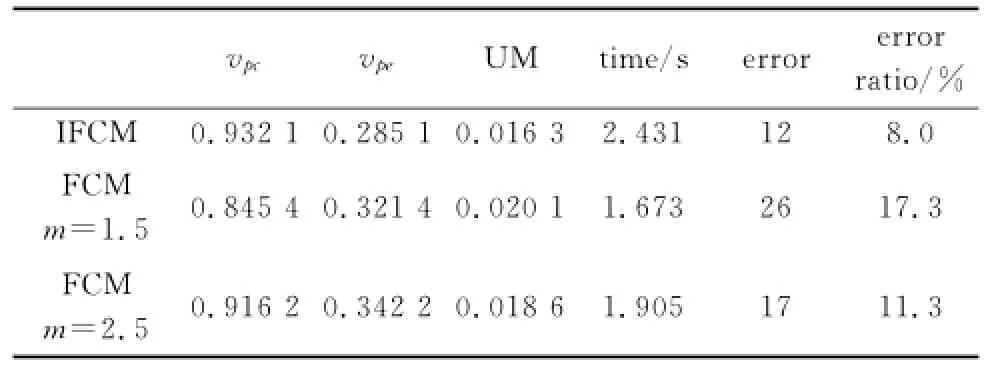
表3 IRIS樣本聚類結果比較

從表3可以看出，當模糊加權指數m取不同值時，對標準測試數據集IRIS的模糊聚類效果不一樣。其中，當模糊加權指數取區間型值時，其劃分系數vpc最大，而劃分熵vpe、均勻性測度UM以及錯分率最低，表明其聚類效果好。另外，當m取單個值時，只要其值在一定范圍內，其聚類效果的好壞難以評價，例如本實驗中，當m＝1.5或m＝2．5時，兩種情況下FCM聚類劃分的效果難以比較。

上面分別從圖像分割對比實驗、劃分類大小非均衡的人造數據劃分實驗以及標準測試樣本IRIS聚類對比實驗中，分析了模糊化參數對模糊聚類的影響，得出了區間型模糊化參數在模糊聚類中有較好的劃分效果，但區間型模糊化參數在聚類劃分過程中，由于計算復雜，故其計算耗時比經典的FCM算法要多，這一點從上述實驗結果中可以明顯看出，有關計算時間復雜度的分析受篇幅所限，本文未有述及。

5 結 論

本文通過分析經典FCM聚類算法中模糊加權指數m取值存在的困難及不確定性現狀，提出了一種區間型模糊加權指數設計模型，并由此探討了包括模糊隸屬度、模糊聚類中心在內的模糊化參數模型的設計方法。實驗的結果分析表明，采用區間型模糊化參數方法，不但可以較好解決樣本集劃分類之間差別懸殊問題，而且使劃分結果更好，細節更詳盡，特別對噪聲干擾的數據劃分有很強的魯棒性。但是，在實際應用中，該方法還存在如下幾個問題亟待解決：一是由于采用區間型參數計算，其計算復雜度較高，數據處理時間長；二是模糊加權指數的區間值大小是根據不同劃分類樣本而主觀設計的，到底取多少沒有統一標準和規范化方法，這些問題也正是作者及課題組成員下一步要研究解決的問題。同時需要指出，本文針對FCM聚類算法本身的參數進行區間化研究，與相關文獻［19- 20］中提出的區間型數據的聚類研究是兩個不同的概念，如何將這兩者聯系起來進行研究，即采用區間型模糊化參數研究區間型數據集，這也是我們正在研究的范疇。

［1］Ji Z X，Pan Y，Chen Q，et al．Natural image segmentation algorithm with unsupervised FCM［J］．Journal of Image and Graphics，2011，16（5）：773- 783．（紀則軒，潘瑜，陳強，等．無監督模糊C均值聚類自然圖像分割算法［J］．中國圖象圖形學報，2011，16（5）：773- 783．）

［2］Tan K S，Lim W H，Isa N A M．Novel initialization scheme for fuzzy C-means algorithm on color image segmentation［J］．Applied Soft Computing，2013，13（4）：1832- 1852．

［3］Chen J S，Pi D C，Liu Z P．An insensitivity fuzzy C-means clustering algorithm based on penalty factor［J］．Journal of Software，2013，8（9）：2379- 2384．

［4］Sambasivam S，Theodosopoulos N．Advanced data clustering methods of mining web documents［J］．Issues in Informing Science and Information Technology，2006（3）：563- 579．

［5］Wang D D，Li B，Chen W F，et al．An improved FCM algorithm based on multiple objective programming［J］．Journal of Image and Graphics，2008，13（8）：1492- 1495．（王丹丹，李彬，陳武凡．基于多目標規劃的模糊C均值聚類算法［J］．中國圖象圖形學報，2008，13（8）：1492- 1495．）

［6］Mendel J．Uncertain rule-based fuzzy logic systems：introduction and new directions［D］．Upper Saddle River：Drentice-Hall，2001．

［7］Zhai D，Mendel J M．Uncertainty measures for general type-2 fuzzy sets［J］．Information Sciences，2011，181（3）：503- 518．

［8］Hwang C，Rhee F C H．Uncertain fuzzy clustering：interval Type-2 fuzzy approach to C-means［J］．IEEE Trans.on Fuzzy System，2007，15（1）：107- 120．

［9］Ondrej L，Milos M．General Type-2 fuzzy C-means algorithm for uncertain fuzzy clustering［J］．IEEE Trans.on Fuzzy System，2012，20（5）：883- 897．

［10］Bezdek J C．Pattern recognition with fuzzy objective function algorithm［M］．New York：Plenum Press，1981．

［11］Pal N R，Bezdek J C．On clustering for the fuzzy C-means modeling［J］．IEEE Trans.on Fuzzy System，1995，3（3）：370 -379．

［12］Gong G Y，Gao X B，Wu Z D．An optimal choice method of parameter m in FCM clustering algorithm［J］．Fuzzy Systems and Mathematics，2005，19（1）：143- 147．（宮改云，高新波，伍忠東．FCM聚類算法中模糊加權指數m的優選方法［J］．模糊系統與數學，2005，19（1）：143- 147．）

［13］Wang J，Wang S T．Double indices FCM algorithm based on hybrid distance metric learning［J］．Journal of Software，2010，21（8）：1878- 1888．（王駿，王士同．基于混合距離學習的雙指數模糊C均值算法［J］．軟件學報，2010，21（8）：1878- 1888．）

［14］Wang Z H，Liu Z J，Chen D H．Research of PSO-based fuzzy C-means clustering algorithm［J］．Computer Science，2012，39（9）：166- 169．（王縱虎，劉志鏡，陳東輝．基于粒子群優化的模糊C均值聚類算法研究［J］．計算機科學，2012，39（9）：166- 169．）

［15］Kannan S R，Ramathilagam S，Chung P C．Effective fuzzy C-means clustering algorithms for data clustering problems［J］．Expert System with Applications，2012，39（7）：6292- 6300．

［16］Wang X E，Han D Q，Han C Z．Selection method for parameters of rough fuzzy C-means clustering based on uncertainty measurement［J］．Journal of Xi’an Jiaotong University，2013，47（6）：55- 61．（王學恩，韓德強，韓崇昭．采用不確定性度量的粗糙模糊C均值聚類參數獲取方法［J］．西安交通大學學報，2013，47（6）：55- 61．）

［17］Wu J J，Xiang H，Liu C，et al．A generalization of distance functions for fuzzy C-means clustering with Centroids of arithmetic means［J］．IEEE Trans.on Fuzzy System，2012，20（3）：557- 571．

［18］Newman D J，Hettich S，Blake C L，et al．UCI repository of machine learning databases［EB／OL］．［2014- 04- 08］．http：∥www．ics．uci．edu／～mlearn／ML-Repository．html．

［19］Chen J S，Pi D C．Improved fuzzy C-means model based on quadratic［J］．Systems Engineering and Electronics，2013，35（7）：1548- 1553．

［20］Li D，Gu H，Zhang L Y．A fuzzy C-means clustering algorithm based on nearest-neighbor intervals for incomplete data［J］．Expert System With Applications，2010，37（10）：6942- 6947．

Interval type fuzzifier parameter model in fuzzy C-means clustering

XIAO Man-sheng1，2，XIAO Zhe1，WEN Zhi-qiang2，YU Hui-jun1
（1.College of Science and Technology，Hunan University of Technology，Zhuzhou 412008，China；2.College of Computer and Communication，Hunan University of Technology，Zhuzhou 412008，China）

Aiming at the problem about the effect of the fuzzy weighted index in classical fuzzy C-means clustering algorithm and the value of uncertainty，the model of interval type fuzzy weighted index is proposed．Theoretical basis of the model and its effect on the clustering results are analyzed．Based on this model，the fuzzifier parameter such as fuzzy membership partition matrix，fuzzy clustering center representation is derived．The theoretical analysis and experimental results show that the interval type fuzzifier parameter model designing has achieved good effect based on data processing of fuzzy partition

fuzzy C-Means（FCM）；interval fuzzy weighted index；fuzzifier parameter；uncertainty

TP 391

A

10．3969／j．issn．1001-506X．2015．04．22

肖滿生（1968-），男，教授，主要研究方向為智能計算和智能信息處理。E-mail：xiaomansheng＠tom．com

肖 哲（1977-），女，講師，碩士，主要研究方向為智能信息處理。E-mail：snakexz＠sina．com

文志強（1973-），男，副教授，博士，主要研究方向為數據挖掘和圖像處理。E-mail：zhqwen20001＠163．com

于惠鈞（1975-），男，副教授，主要研究方向為數據挖掘、智能控制。E-mail：463298180＠qq．com

1001-506X（2015）04-0868-06

2014- 04- 21；

2014- 09- 01；網絡優先出版日期：2014- 10- 30。

網絡優先出版地址：http：／／w ww．cnki．net／kcms／detail／11．2422．TN．20141030．1134．011．html

國家自然科學基金（61170102）；湖南省自然科學基金（13JJ9017）；湖南省教育廳科研項目（13C032）資助課題