艦載機多機一體化機務保障調度方法

韓 維，蘇析超，陳俊鋒

（1．海軍航空工程學院飛行器工程系，山東煙臺264001；2．海軍航空工程學院研究生管理大隊，山東煙臺264001）

艦載機多機一體化機務保障調度方法

韓 維1，蘇析超2，陳俊鋒2

（1．海軍航空工程學院飛行器工程系，山東煙臺264001；2．海軍航空工程學院研究生管理大隊，山東煙臺264001）

為了有效提升艦載機多機機務保障的效率和保障人員的利用率，根據單機機務保障流程約束特性，建立了基于多計劃評審技術網絡的多目標多機一體化機務保障調度模型。針對問題的求解，提出了一種自適應混合差分進化算法。首先根據調度的網絡化排隊過程，設計了基于事件調度策略的解碼方法。其次為了協調算法“探索”與“開發”的能力，引入了自適應的變異操作和交叉、變異參數控制。再次，針對工序塊的平行組合排列特征，提出了4種鄰域結構，進而在算法框架中嵌入了一種自適應多鄰域局部搜索策略。最后通過仿真實驗驗證了模型和算法的可行性和有效性。

艦載機機務保障；多目標優化；差分進化算法；局部搜索

0 引 言

作為現代戰場上的“海上霸王”，航空母艦及其艦載機航空兵擺脫了海面的二維限制，一直占據著軍事大國海軍裝備序列中的核心地位。在航母編隊中，艦載機是最關鍵的組成部分，航母全系統和航母戰斗群的絕大多數作戰使命都需要并且只能由艦載機來承擔和完成［1］。其中，艦載機艦面保障作業調度時間跨度長，涉及面廣，約束條件復雜，如何對其提供合理的規劃或優化對提升艦載機作戰效能具有重要作用。

目前國內外對艦載機調度方法的研究主要集中在人工智能領域。文獻［2］針對艦載機甲板布列出動問題建立了布列調度多目標優化模型，并利用改進的混合粒子群優化（hybrid particle swarm optimization，HPSO）算法和遺傳算法（genetic algorithm，GA）進行求解和對比。文獻［3］采用多智能體技術，將艦載機維修保障過程建立為三層多智能體系統模型，并成功運用于保障人員配置問題的求解。文獻［4］通過對一款名為甲板運作行動過程規劃者（deck operation course of action planner，DCAP）的輔助飛行甲板管理軟件的開發，研究了反向強化學習方法［5］和基于排隊網絡的策略優化［6］在艦載機自適應多階段調度問題中的應用，并通過甲板作業仿真，將基于線性整數規劃模型的優化算法與傳統的專家啟發式規則進行調度性能上的對比［7］。文獻［8］根據所建立的艦載機運動約束模型采用改進A*算法求解，具有規劃路徑平滑且響應速度快等特點。航空機務保障方面，陸基機務保障主要采取固定機組制模式，存在人員利用率不高、保障缺乏彈性等特點，若應用于空間有限的艦面多機保障或將導致人員擁擠和危險系數增高等后果，因此，研究基于任務的艦載機多機一體化機務保障調度具有較強的現實意義。文獻［9］和文獻［10］分別將多機機務保障問題抽象為柔性開放車間和柔性流水車間問題，但均是基于工序串行約束的簡化模型，這與艦載機保障工序復雜網絡化約束的實際不符。

為此本文按照艦載機保障流程約束特性，以最小化保障時間和保障主體負載均衡為目標，建立基于多計劃評審技術（multiple program evaluation and review technique，Multi-PERT）網絡的多機一體化機務保障模型。設計了一種嵌入多鄰域結構局部搜索的自適應混合差分進化（self-adaptive hybrid differential evolution，SaHDE）算法求解該模型。通過實例仿真和與其他調度算法的對比驗證了算法的可行性和有效性。

1 艦載機多機一體化機務保障調度問題模型

1.1 保障作業流程分析與問題描述

艦載機多機一體化機務保障調度是指在單機保障流程約束下，通過合理調度保障單元，對多機型機群同時進行保障，以達到較優的出動效能和較高的保障資源利用率。在一體化保障模式下，保障單元可以擺脫固定機組模式的束縛，實現在不同艦載機之間的轉換和保障。納入一體化保障模式的艦載機可包含戰斗機、攻擊機、預警機、反潛機、電子戰飛機等固定翼艦載機，且不同艦載機由于任務的區別而導致保障作業時間上的差異。艦載機單機保障作業根據保障的內容和性質劃分為不同的專業類別，每一專業類別的工序由與之對應的若干組保障單元負責保障，而每個保障單元可由若干保障人員組成，如掛彈單元（可由2～4人組成）主要負責軍械外觀檢查、掛架準備、填充炮彈和掛載導彈等軍械類保障工序。且出于安全性和空間限制的考慮，不同工序間存在串、并行的約束關系。因此，本文通過構建Multi-PERT多機保障網絡對多機一體化機務保障調度進行描述。圖1所示為某波次出動簡化的Multi-PERT多機保障網絡圖。

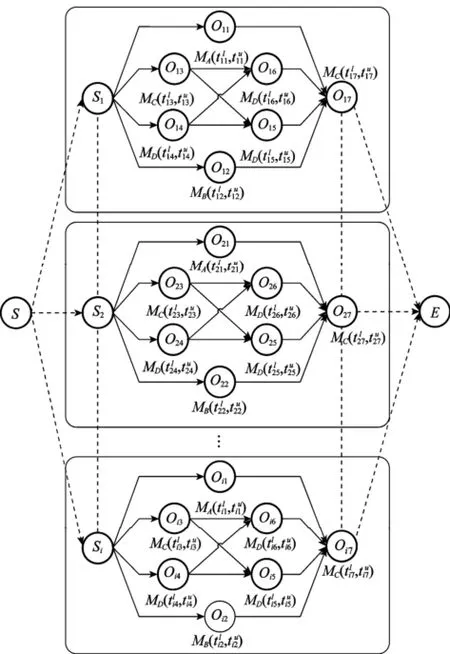
圖1 Multi-PERT多機保障網絡圖

圖1 中Oij為艦載機i的第j項工序表示工序Oij由MA類保障單元負責，且由于保障單元的技能經驗、協作能力等的差異，其保障時間的取值范圍為S和E分別為合成保障過程的虛擬開始和虛擬結束作業，Si為第i架艦載機的入場保障起始虛工序，Si之間的虛線表示入場保障的前后時間約束，Oi7之間的虛線則表示各艦載機保障結束時間的優先級約束。

在此基礎上，為建立艦載機多機一體化機務保障調度優化問題模型，進行如下假設：①同一時刻某一工序只能接受一個保障單元保障；②保障單元在保障某工序的過程不可中斷，且只能在上一道工序完成后才能進行下一道工序保障；③各艦載機保障項目之間除共享保障單元外，相互獨立；④艦載機在各站位均能接受油電氣液等“一站式”資源保障，無需中途轉運；⑤不考慮突發故障和其他干擾因素。

根據上述分析可以看出，艦載機多機一體化機務保障調度優化問題本質上屬于資源約束條件下多項目調度優化問題［1112］，但主要存在兩個方面的不同，一是本文的Multi-PERT多機保障模型是基于相同的單機PERT保障模型而建立的，即各項目（單機保障工序集合）具有相同保障流程；二是本文的調度問題不僅包括各項目工序的優先排序，還包括各項目工序在資源（保障單元）上的選擇分配，問題的復雜性更高。

1.2 調度模型參數及決策變量定義

模型中各參數定義如下：

I＝｛1，2，…，n｝為參與保障的艦載機集合，其中，n為艦載機數量。

M＝｛1，2，…，｜M｜｝為保障單元集合，其中，｜M｜為保障單元數量。

Ji＝｛1，2，…，m｝為艦載機i的工序集，其中，m為單機工序數。

Mj為可對工序Oij進行保障的一類保障單元集合，且Mj?M。

Sij為艦載機i的第j道工序保障開始時間。TSi為艦載機i的入場保障起始時間。

Eij為艦載機i的第j道工序保障結束時間。

Tijk為艦載機i的第j道工序在第k（k∈Mj）個保障單元上的作業時間。

Pij為工序Oij的緊前工序集合。

HSi為虛工序Si的緊后工序集合。

Ci為艦載機i最后一道工序的保障結束時間。

Cmax為各艦載機的最大保障結束時間。

Cijeg為保障單元從艦載機i的第j道工序保障結束至艦載機e的第g道工序開始保障的轉換時間。

ObVk為第k（k∈Mj）個保障組的閑忙比，即整個保障過程空閑時間與工作時間的比值。Eob為保障單元的閑忙比方差。決策變量定義為

1.3 調度模型的建立

根據艦載機保障調度的實際需求，調度優化的目的首先要提升保障效率，使得保障活動在最短的時間內完成；在保證保障時間最短的前提下，其次是使得保障單元的工作負載均衡化。因此選取最大保障完工時間Cmax＝max（Ci）和閑忙比方差Eob兩個指標作為優化目標。根據定義可得

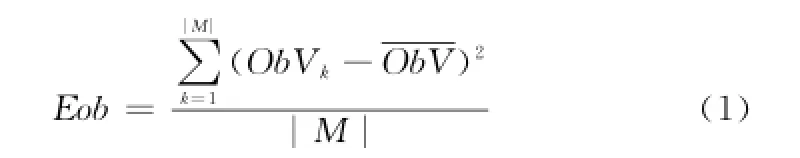
其中，保障單元k的閑忙比為

工作時間bVk可表示為保障時間和轉移時間之和，即

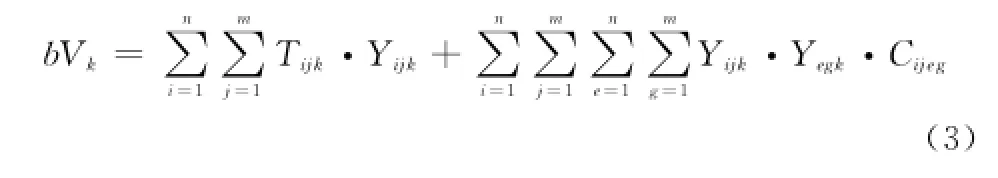
綜合考慮保障的目標及各類約束，建立艦載機多機一體化機務保障調度優化模型為

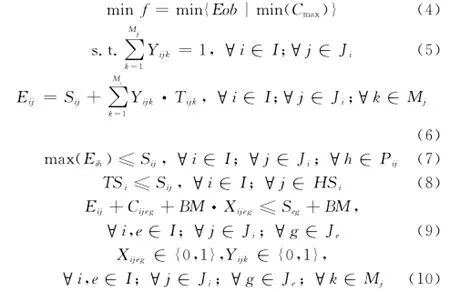
其中，式（4）表示調度的目標，即在保證最小化最大保障完工時間的前提下，使得各保障單元閑忙比更為均衡；式（5）表示每架艦載機的任一工序只能在一個保障單元上保障；式（6）表示任一艦載機工序保障開始時間與結束時間的關系；式（7）表示作業的緊前關系約束，一個工序的開始必須保證所有緊前工序均保障結束；式（8）表示艦載機在入場系留后才能開始保障；（9）表示不同工序不能同時由同一保障單元保障，且保障按優先級進行，式中BM為足夠大實數，確保不等式恒成立；式（10）表示決策變量的0－1屬性約束。

2 基于SaHDE算法的問題求解

艦載機多機一體化機務保障調度問題是一類具有高度復雜性、多約束性和多目標性的NP-hard問題。艦載機保障工序眾多，且隨著艦載機保障數量的增加，問題的規模急劇增大，導致在問題的求解過程中容易陷入局部極值而找不到全局最優解。通過增大搜索空間和種群規模可在一定程度上增加得到全局最優解的概率，但無疑將耗費更大的計算量，降低搜索的效率。差分進化算法（differential evolution，DE）由Storn和Price提出后，便被證明是最強大的隨機實參數優化算法之一［13］，在解決實際調度問題具有很強的適應性和普遍性［14-15］，并在諸如本文的多極值問題方面具有更優秀的求解能力［16］。本節在標準DE算法［17］的基礎上，設計了改進的SaHDE算法。

2.1 染色體編碼

經典資源受限多項目調度問題的求解常采用離散作業列表編碼方式和隨機數編碼。若采用作業列表編碼方式，則只能表示各艦載機作業的保障順序，針對每道工序所選擇的保障單元則還需增加一層編碼列表加以表示。為降低編碼的冗雜性，克服作業列表編碼方式在進化操作中產生非法解的不足，本文采用基于矩陣的實數編碼方式［14］。

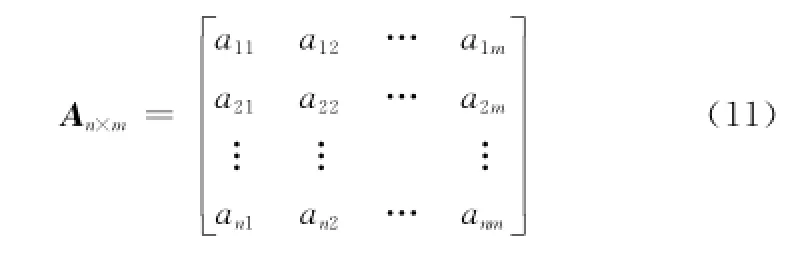
式中，個體An×m，行表示艦載機編號，列表示工序號，任一元素aij為區間（1，Mj＋1）上的一個隨機實數。其中，整數部分Int（aij）表示艦載機i的第j道工序在第Int（aij）個保障單元上作業，小數部分Dec（aij）表示多個工序在同一保障單元上沖突時的優先排序，Dec（aij）越大代表優先級越高。將矩陣編碼的每一列構成一小段，形成的染色體可以表示為一個長度為n×m的字符串：［a11，a21，…，an1，a12，a22，…，anm］。

2.2解碼操作

解碼過程是實現染色體向調度方案映射的過程，每一次解碼都是對調度系統的一次仿真。根據Multi-PERT多機保障網絡圖可以看出，解碼的每一步不僅取決于染色體上的信息，還需對工序的緊前緊后約束進行判斷。不妨將艦載機多機機務保障調度看作是包含多種平行保障單元的網絡化排隊保障過程，任一道工序在滿足緊前約束條件下釋放到所選擇的保障單元上，并根據優先級進行排隊保障。本文采用離散事件仿真中的事件調度策略，通過基于最早發生事件的時鐘推進機制，得到各個工序保障的起止時間等調度信息。

因此首先定義3類事件歷程：E1-艦載機入場，E2-工序保障開始，E3-工序保障結束，每種事件分別設置相對應的未來事件表FEL1、FEL2和FEL3。記仿真時鐘為TIME，第k個保障單元的等待保障工序隊列集為Wk，執行保障工序集為Ak，已完成保障工序集為Ck。調度的每一步時鐘推進到3類未來事件表中最早發生的時間，并處理對應的事件歷程：

事件1 艦載機i入場，并將虛工序Si的緊后工序集HSi中的工序按照Int（aij）釋放至對應的保障單元隊列Wk，并更新FEL1。

事件2 第k個保障單元上的工序Oij保障開始，記錄Sij并更新FEL2和FEL3。

事件3 第k個保障單元上的工序Oij保障結束，記錄Eij，將Ak中元素轉移至Ck，并判斷Oij緊后工序的緊前工序集PHij是否均已保障結束，若是，則釋放緊后工序集Hij至對應的保障單元隊列。根據Dec（aij）選取Wk中下一保障工序，并將其轉移至Ak，并更新FEL2和FEL3。

基于事件調度策略的解碼（decoding algorithm based on event scheduling，DAES）算法描述如表1所示。

表1 DAES算法的偽代碼

續表

2.3 自適應變異操作

基于種群的智能優化算法實現良好搜索性能的關鍵在于尋找“探索”與“開發”上的平衡，前者意味著算法“探索”或者“搜索”可行解空間各個區域的能力，后者則表示算法盡快收斂于近似最優解的能力。在常見的5種變異算子中［17］，DE／rand／1和DE／rand／2變異策略以種群中的隨機個體作為基本向量，有利于保持種群的多樣性，但進化方向缺乏集中性，收斂速度慢；DE／best／1和DE／best／2變異策略以父代最優個體作引導，局部搜索能力強，精度高，但容易陷入局部最優而出現早熟；而DE／current-to-best／1變異策略采取本地個體與最優個體加權求和作為基本向量，在一定程度上平衡了全局尋優能力和收斂速度，但權重系數僅取決于縮放因子F，無法根據進化信息進行自適應調節。

受文獻［18］的啟發，本文在DE／current-to-best／1變異策略的基礎上提出如下的改進：

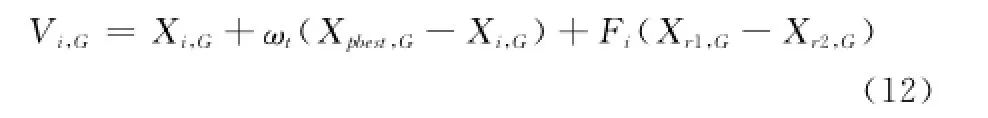
式中，Xpbest，G是從當前種群的100p%的最優子種群中隨機選取的個體；ωt為Xpbest，G與Xi，G的權重系數，為使得算法在前期執行階段更注重“探索”，而在后偏向“開發”，加快收斂速度，對ωt采用非線性sigmoid遞增函數

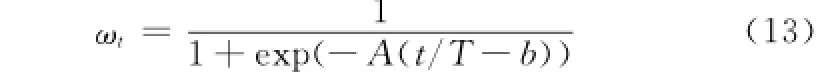
式中，t為當前迭代次數；T為最大迭代次數；參數A控制曲線曲率大小，A越小，則ωt越接近于直線增長；參數b控制由“探索”轉向“開發”的時機，當b＝0.5時，ωt隨t的增加呈“S”型曲線增長，且在t＝T／2處ωt＝0.5。b值越小，說明由Xi，G為主導的搜索占總搜索過程的比例則越少，由探索轉入開發的時機越早。因此可通過對參數A和b的控制，整體把握 “探索”與“開發”上的平衡。

2.4 自適應參數控制

除變異策略外，縮放因子F和交叉概率CR同樣對搜索的性能起到重要作用。為了更好地利用種群信息以提升F與CR在迭代過程中的自適應性，本文采用種群多樣性測試函數定義為

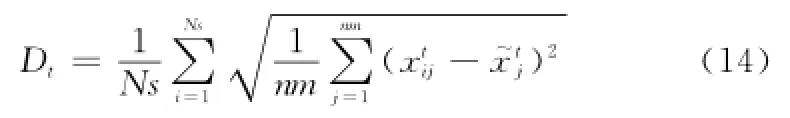
式中，Ns為種群規模；nm為染色體長度；ˉxtj表示第t次迭代時群體平均中心位置的第j維分量。Dt越小，則個體內特征差異值越小，種群的多樣性越低。通過對式（13）的變換，本文設計了一種基于種群多樣性的參數自適應變化策略，表示為

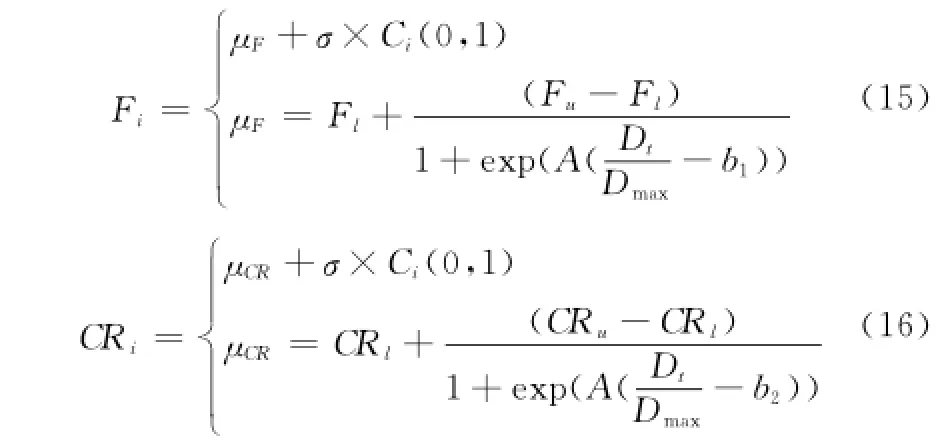
式中，Dmax＝max｛Dt′，t′＝1，2，…，t｝；Fl、Fu、CRl、CRu分別為縮放因子和交叉概率的最小、最大邊界，擾動項采用范圍更廣的柯西分布；σ為人為給定的分布標準差，按經驗取為0.1。在進化過程中，縮放因子和交叉概率隨著種群多樣性的變化而自適應變化，當種群多樣性較高時，Fi和CRi縮小，增強種群的開發能力，加快收斂；反之當種群多樣性較低，Fi和CRi增大，以增強種群跳出局部極值的能力，避免早熟收斂。基于柯西分布的擾動項一方面增加了參數的多樣性，另一方面其相對于正態分布具有更強的兩翼性，從而加大了尋優范圍和跳出局部最優點的能力。

2.5 基于自適應多鄰域結構的局部搜索

針對調度問題解空間的多極值性質，通過引入局部搜索可有助于引導算法高效到達存在眾多局部極小的峽谷底部，并進行徹底的搜索［19］。而局部搜索的性能取決于所使用的鄰域結構。

首先根據染色體中aij對應的Int（aij）值將所有工序分配至各保障單元，再根據Dec（aij）值對保障單元內的工序隊列按照由小到大排列得到πk＝｛Oij｜（k＝Int（aij））∧（k∈Mj）｝。由此，對?i∈I的第j道工序集，均可對應｜Mj｜個排序πk（k∈Mj）。針對上述平行工序排序，定義基于工序塊的4種鄰域結構如下：

（1）縱向交換鄰域Interchange_V（πk1，u，πk2）：表示對?k1，k2∈Mj（k1≠k2），將πk1中第u位工序與πk2中各個工序依次交換位置。

（2）橫向交換鄰域Interchange_L（πk，u）：表示對?k∈Mj，將πk中第u位工序與πk中其他位工序依次交換。

（3）縱向插入鄰域Insert_V（πk1，u，πk2）：表示對?k1，k2∈Mj（k1≠k2），將πk1中第u位工序取出，并依次插入至πk2中各個可插入位置。

（4）橫向插入鄰域Insert_L（πk，u）：表示對?k∈Mj，將πk中第u位工序取出，并依次分別插入πk中其他可插入位置。

其中，針對具體的交換和插入操作，可假設第u位工序Oij，第v位工序Oej和第v＋1位工序Ofj。若令工序Oij與工序Oej交換，則令aij值與aej值互換；若令工序Oij插入至第v位和第v＋1之間的空位，則令aij＝aej＋（afj－aej）· rand（0，1）。

顯然，不同的鄰域結構具有不同的局部搜索效果。橫向交換鄰域與橫向插入鄰域是通過改變單個保障單元內工序順序進行局部搜索，而縱向插入鄰域與縱向交換鄰域則通過改變平行保障單元間工序位置進行局部搜索，且縱向插入鄰域可改變保障單元內工序數量，對搜索前期起到平衡保障單元負載的作用，縱向交換鄰域則不會改變保障單元內工序數量，這在搜索后期保障單元負載較均衡的情況下將發揮更大作用。

為了更有效地利用各種鄰域結構的特點，借鑒文獻［20］中SaDE算法的自適應變異策略，以上述定義的4種鄰域結構作為局部搜索的選擇對象，根據算法搜索過程中各鄰域的貢獻動態改變其使用率，進而達到自學習的搜索效果。具體算法過程描述如下：

步驟1 令pl（l＝1，2，3，4）表示第l種鄰域結構的選擇概率和分別表示第t（t＞LP）次迭代時之前LP代中第l種鄰域結構搜索產生個體進入下一代的成功或是失敗的數目表示第l種鄰域結構搜索進入下一代的個體的成功率，初始化pl（l＝1，2，3，4）＝1／4，令j＝1。

步驟2 選取染色體個體S內工序j的基因段Sj＝（a1j，a2j，…，anj），將其轉換為平行保障單元Mj上的工序排列。

步驟3 采取輪盤賭方式選擇一種鄰域結構L，并隨機選取πk1、u和πk2（k2≠k1）。

步驟4 若L＝Interchange_V，則Snew＝Interchange_ V（πk1，u，πk2）；若f（Snew）＜f（S），則，且S＝ Snew，否則

步驟5 若L＝Interchange_L，則Snew＝Interchange_L（πk1，u）；若f（Snew）＜f（S），則且S＝Snew，否則

步驟6 若L＝Insert_V，則Snew＝Insert_V（πk1，u， πk2）；若f（Snew）＜f（S），則，且S＝Snew，否則

步驟7 若L＝Insert_L，則Snew＝Insert_L（πk1，u）；若f（Snew）＜f（S），則且S＝Snew，否則

步驟8 按式（17）和式（18）更新各鄰域的選擇概率。

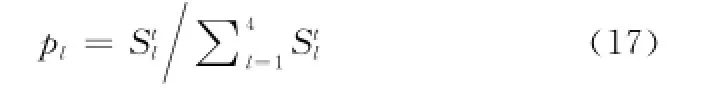
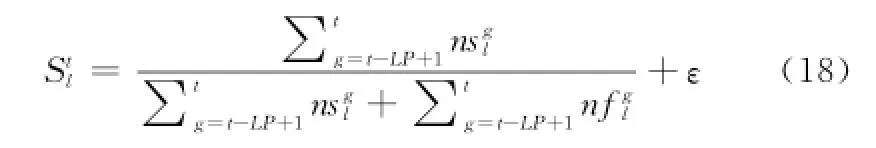
式中，ε為一個較小的值，其作用是控制Stl非零，本文取ε＝0.01。在搜索初期，若t＜LP，則令LP＝t。

步驟9 令j＝j＋1，若j≤m，則轉到步驟2；否則，輸出最優解Snew。

2.6 SaHDE算法流程

基于本文Sa HDE算法求解艦載機多機一體化機務保障調度問題的具體步驟描述如下：

步驟1 初始化種群規模Ns，最優子種群比例p，最大迭代次數T，縮放因子和交叉概率的最小最大邊界Fl、Fu、CRl、CRu，自適應控制參數A、b、b1、b2，保障艦載機數量n及各艦載機工序數m。記種群基因位aij的取值下界lower（aij）＝1，上界upper（aij）＝｜Mj｜＋1，對種群各染色體基因位按aij＝1＋｜Mj｜·rand（0，1）進行初始化。

步驟2 按第2.2節DAES算法解碼得到調度方案及種群個體適應度。

步驟3 根據式（14）計算種群多樣性，并根據式（15）求得縮放因子Fi。

步驟4 選取100p%的最優子種群，按式（12）執行變異操作。若aij＜lower（aij），則aij＝2·lower（aij）－aij；若aij＞up per（aij），則aij＝2·up per（aij）－aij。

步驟5 根據式（16）求得交叉概率CRi，并進行二項交叉操作。

步驟6 對新種群進行解碼，采取貪婪選擇方式生成新種群。

步驟7 選取100p%的最優子種群，執行基于自適應多鄰域結構的局部搜索。

步驟8 判斷是否達到最大循環代數，若是，則輸出最優調度方案；若否，則轉入步驟2循環計算。

3 仿真分析

為驗證本文模型的可行性和算法的有效性，結合保障的約束條件，建立一般化艦載機單機機務保障流程如圖2所示。進一步簡化，對單機機務保障網絡流程中的串行工序進行合并，例如可將飛機下部機械檢查和飛機上部機械檢查合并為機械外觀檢查工序，最終可得到如圖1所示的Multi-PERT多機保障網絡圖，其中包含4類平行保障單元。

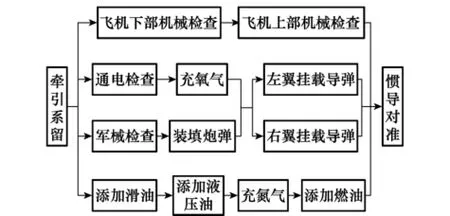
圖2 艦載機單機機務保障流程圖

以俄羅斯庫茲涅佐夫號航母為仿真背景，任務想定A需要保障12架艦載機，并給出各架艦載機完成任務所需的掛彈加油等工序保障的需求量，參與保障的各類保障單元數量為｜MA｜＝3，｜MB｜＝3，｜MC｜＝4，｜MD｜＝5。各架艦載機通過機庫和甲板上的調運計劃得到的入場時間和布列站位如圖3所示，其中未標明入場時間的艦載機表示TSi＝0。

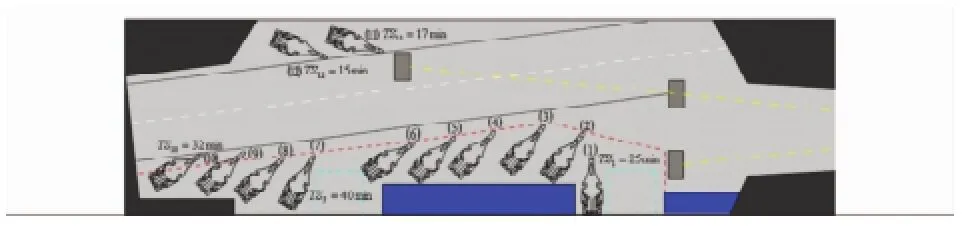
圖3 艦載機站位及入場時序示意圖

利用Matlab8.1軟件編制仿真程序，參數設置為：種群規模Ns＝50，最優子種群比例p＝0.1，最大迭代次數T＝400，縮放因子和交叉概率的最小最大邊界Fl＝0.3，Fu＝0.6，CRl＝0.6，CRu＝0.9，自適應控制參數A＝10，b＝0.2，b1＝b2＝0.5，學習周期LP＝30。

定義自適應差分進化算法（adaptive differential evolution algorithm，ADE）為在本文SaHDE算法基礎上不采用局部搜索機制，DE1算法為采用DE／best／1／bin模式的標準DE算法，DE2算法為采用DE／rand／1／bin模式的標準DE算法，且DE1和DE2設置參數為F＝0.5，CR＝0．9。分別采用本文的SaHDE算法、GA算法、ADE算法、DE1和DE2進行30次獨立運算，得到的結果如表1所示，其中，BST，AST，BOB和AOB分別表示30次運行結果所得的最優保障完工時間、平均保障完工時間、最小閑忙比方差和平均閑忙比方差。

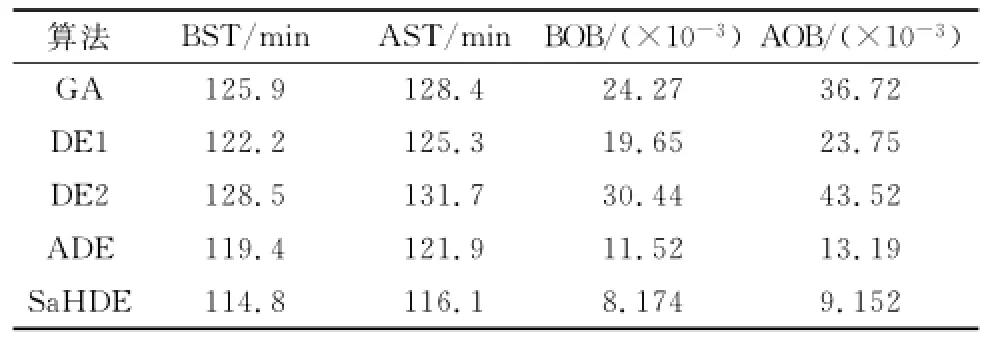
表2 算法性能對比

圖4為DE1、DE2和ADE算法求得的保障時間最優解收斂對比曲線，圖5為SaHDE算法、ADE算法和GA求得的保障時間最優解收斂對比曲線。

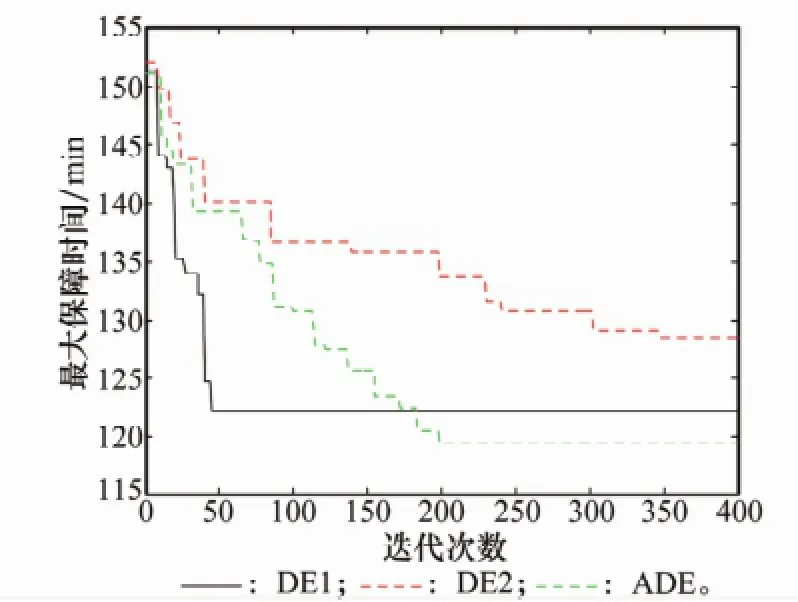
圖4 DE1、DE2和ADE算法最優解收斂對比曲線

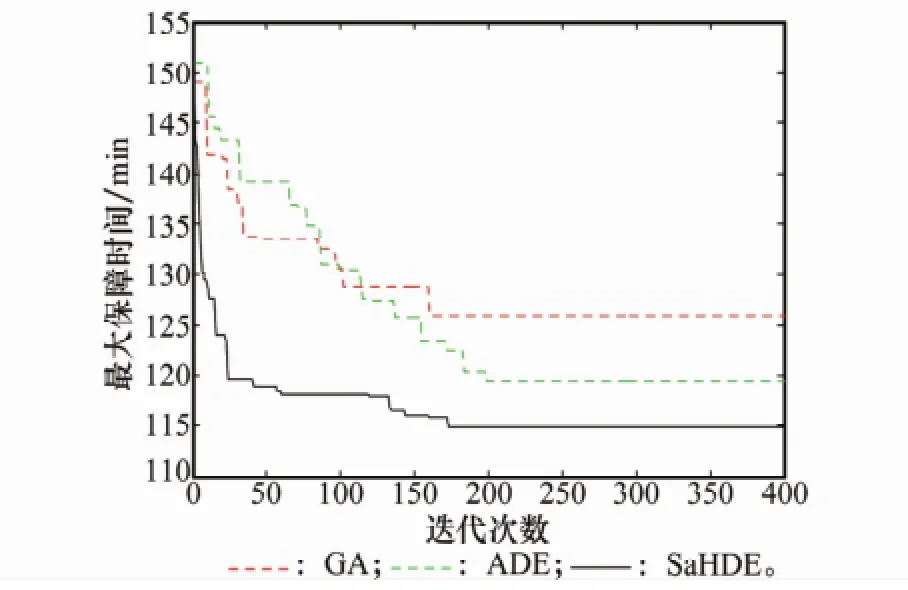
圖5 GA、ADE和SaHDE算法最優解收斂對比曲線

結合表1、圖4和圖5可以看出：①在求解本文的多峰值問題的標準算法中，DE1的性能優于DE2和GA，收斂速度快，但易于陷入局部極值。②ADE通過引入自適應的變異策略和參數控制策略，結合了DE1的“探索”和DE2與“開發”的優勢，性能較DE1和DE2均有所提升。③Sa HDE算法在ADE算法的基礎上，引入自適應多鄰域的局部搜索，進一步增強了算法跳出局部極值、避免早熟收斂的能力，同時具備較強的魯棒性。

通過Sa HDE算法獲得的一個最優調度甘特圖如圖6所示，其每一個條狀框圖中的前一個字母下標的數字表示正在保障的艦載機i（1≤i≤12），后一個數字表示艦載機的第j（1≤j≤7）道工序；陰影部分代表保障單元的轉移時間；坐標縱軸對應保障單元，如表示A類保障單元中的第一組。所求得最優目標值Cmax＝114.8min，Eob＝8.174 ×10－3。

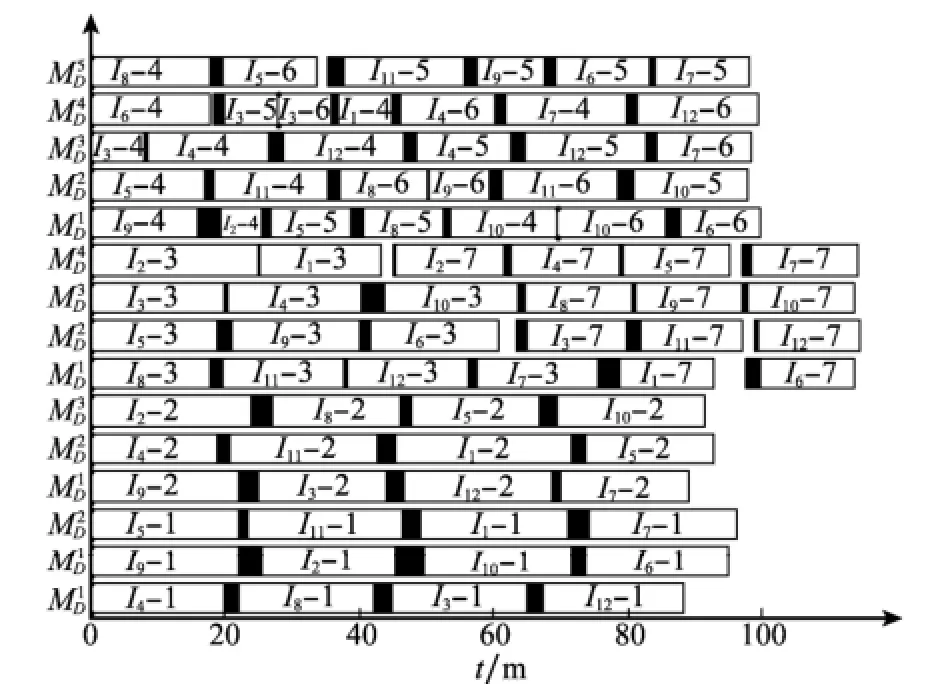
圖6 最優調度甘特圖

4 結 論

本文在分析艦載機單機機務保障流程的基礎上，以最小化保障時間和保障主體負載均衡為目標，建立基于Multi-PERT網絡的多機一體化機務保障模型。設計了一種嵌入多鄰域結構局部搜索的自適應混合差分進化算法Sa HDE求解該模型。最后通過實例仿真和對比，驗證了模型的可行性與所提出算法的優越性，對航母上的多機機務保障調度提供了新的思路和決策參考。

［1］Han W，Wang Q G．Conspectus of aircraft carrier and carrier plane［M］．Yantai：Naval Aeronautical and Astronautical University Press，2009：37- 41．（韓維，王慶官．航母與艦載機概論［M］．煙臺：海軍航空工程學院出版社，2009：37- 41．）

［2］Si W C，Han W，Shi W W．Comparison of deck-disposed methods for shipboard aircraft based on HPSO and GA［J］．Systems Engineering and Electronic，2013，35（2）：338- 344．（司維超，韓維，史瑋韋．基于HPSO和GA算法的艦載機甲板布放方法比較［J］．系統工程與電子技術，2013，35（2）：338- 344．）

［3］Feng Q，Li S J，Sun B．A multi-agent based intelligent configuration method for aircraft fleet maintenance personnel［J］．Chinese Journal of Aeronautics，2014，27（2）：280- 290．

［4］Ryan J C，Cummings M L，Roy N，et al．Designing an interactive local and global decision support system for aircraft carrier deck scheduling［C］∥Proc.of the AIAA Infotech＠Aerospace Conference，2011：1516．

［5］Michini B，Jonathan P．A human-interactive course of action planner for aircraft carrier deck operations［C］∥Proc.of the AIAA Infotech＠Aerospace Conference，2011：1515．

［6］Dastidar R G，Frazzoli E．A queueing network based approach to distributed aircraft carrier deck scheduling［C］∥Proc.of the AIAA Infotech＠Aerospace Conference，2011：1514．

［7］Ryan J C，Banerjee A G，Cummings M L，et al．Comparing the performance of expert user heuristics and an integer linear program in aircraft carrier deck operations［J］．IEEE Trans.on Cybernetics，2014，44（6）：761- 773．

［8］Wu Y，Qu X J．Path planning for taxi of carrier aircraft launching［J］．Science China Technological Sciences，2013，56（6）：1561- 1570．

［9］Luan X F，Xie J．Research on multi-aircrafts preparation process based on simulation optimization［J］．Computer and Digital Engineering，2010，38（12）：50- 53．（欒孝豐，謝君．基于仿真優化的多機機務準備流程研究［J］．計算機與數字工程，2010，38（12）：50- 53．）

［10］Wei C Q，Chen C L，Wang B R．Study of aircraft support scheduling of aircraft on carrier based on space restriction［J］．Control Engineering of China，2013，20（4）：699- 702．（魏昌全，陳春良，王保乳．基于空間約束的艦載機航空保障調度研究［J］．控制工程，2013，20（4）：699- 702．）

［11］Wang L，Fang C．A hybrid estimation of distribution algorithm for solving the resource-constrained project scheduling problem［J］．Expert Systems with Application，2012，39（3）：2451- 2460．

［12］Wang W X，Wang X，Ge X L，et al．Multi-objective optimization for multi-project scheduling on critical chain［J］．Advance in Engineering Software，2014，68（2）：33- 39．

［13］Zhao Y X，Yang X S，Liu L Q．Newly emerging meta-heuristic optimization methods［M］．Beijing：Science Press，2013：220- 225．（趙玉新，劉利強．新興元啟發式優化方法［M］．北京：科學出版社，2013：220- 225．）

［14］Tang L X，Yue Z，Liu J Y．An improved differential evolution algorithm for practical dynamic scheduling in steelmaking-continuous casting production［J］．IEEE Trans.on Evolutionary Computation，2014，18（2）：209- 225．

［15］Yuan Y，Xu H．Flexible job shop scheduling using hybrid differential evolution algorithms［J］．Computers&Industrial Engineering，2013，65（2）：246- 260．

［16］Das S，Suganthan P N．Differential evolution：a survey of the state-of-the-art［J］．IEEE Trans.on Evolutionary Computation，2011，15（1）：4- 31．

［17］Su H J，Yang Y P，Wang Y J．Research on differential evolution algorithm：a survey［J］．Systems Engineering and Electronic，2008，30（9）：1793- 1797．（蘇海軍，楊煜普，王宇嘉．微分進化算法的研究綜述［J］．系統工程與電子技術，2008，30（9）：1793- 1797．）

［18］Ghosh P，Das S，Zafar H．Adaptive-differential-evolution-based design of two-channel quadrature mirror filter banks for subband coding and data transmission［J］．IEEE Trans.on Systems，Man，and Cybernetics—Part C：Application and Reviews，2012，42（6）：1613- 1623．

［19］Wang H Y，Zhao Y W，Wang W L，et al．New parallel algorithm based on DE for batch splitting job shop scheduling under multiple-resource constraints［J］．Control and Decision，2010，25（11）：1635- 1644．（王海燕，趙燕偉，王萬良，等．兩級差分進化算法求解多資源作業車間批量調度問題［J］．控制與決策，2010，25（11）：1635- 1644．）

［20］Qin A K，Huang V L，Suganthan P N．Differential evolution algorithm with strategy adaptation for global numerical optimization［J］．IEEE Trans.on Evolutionary Computation，2009，13（2）：398- 417．

Integrated maintenance support scheduling method of multi-carrier aircrafts

HAN Wei1，SU Xi-chao2，CHEN Jun-feng2
（1.Department of Airborne Vehicle Engineering，Naval Aeronautical and Astronautical University，Yantai 264001，China；2.Graduate Student’s Brigade，Naval Aeronautical and Astronautical University，Yantai 264001，China）

In order to improve the maintenance support efficiency and support personnel availability of multi-carrier aircrafts effectively，according to the constraint characteristics of maintenance support process for single-carrier aircraft，a multi-objective integrated maintenance support scheduling model of multi-carrier aircrafts based on multiple program evaluation and review technique networks is established．To solve the problem，a self-adaptive hybrid differential evolution algorithm is presented．First，a decoding method based on event scheduling is designed according to networked queuing process of scheduling．Second，for coordinating the exploration and exploitation in algorithm，a self-adaptive mutation operation，an adaptive control strategy of crossover and mutation parameters are introduced．Third，in view of the characteristics of parallel-arrangement of process blocks，four kinds of neighborhood structure are defined，and then a novel local search based on the newly defined neighborhoods is presented and imbedded in the Sa HDE algorithm．The simulation results show the feasibility of the model and the effectiveness of the algorithm．

carrier aircraft maintenance support；multi-objective optimization；differential evolution algorithm；local search

TP 301

A

10．3969／j．issn．1001-506X．2015．04．14

韓 維（1970-），教授，博士研究生導師，博士，主要研究方向為航空宇航科學與技術。E-mail：Luckydevilhan＠163．com

1001-506X（2015）04-0809-08

2014- 05- 19；

2014- 07- 04；網絡優先出版日期：2014- 09- 28。

網絡優先出版地址：http：／／w ww．cnki．net／kcms／detail／11．2422．TN．20140928．1625．016．html

國家自然科學基金（51375490）資助課題

蘇析超（1989-），通訊作者，博士研究生，主要研究方向為艦載機技術研究及應用。E-mail：381410529＠qq．com

陳俊鋒（1988-），博士研究生，主要研究方向為艦載機技術研究及應用。E-mail：cjf053221＠126．com