姿態擾動情況下的目標動態RCS分布特性

劉 佳，方 寧，謝擁軍，王寶發

（北京航空航天大學電子信息工程學院，北京100191）

姿態擾動情況下的目標動態RCS分布特性

劉 佳，方 寧，謝擁軍，王寶發

（北京航空航天大學電子信息工程學院，北京100191）

運動目標姿態擾動是靜動態雷達散射截面（radar cross section，RCS）差異的主要來源。造成姿態擾動的因素復雜且不可預估，增加了動態RCS分布特性研究的難度。將圖形電磁計算與蒙特卡羅仿真結合，構建以均勻隨機分布為擾動模型的動態RCS仿真分析平臺。根據靜動態RCS差異的統計分布特性，提出置信區間以及數學期望值的計算方法。選擇兩種運動模式下的飛機目標進行驗證，將所得結果與實際擾動模型的動態RCS進行了比對。結論表明該方法具備較強可操作性和工程應用價值，提高了計算機動態RCS仿真能力，為目標靜動態電磁散射特性一致性評估以及特征庫構建提供了有價值的參考信息和分析方法。

雷達散射截面；圖形電磁計算；動態仿真；蒙特卡羅仿真

0 引 言

雷達散射截面（radar cross section，RCS）反映了目標對雷達波的反射強度，是研究目標電磁散射特性的重要參數。在獲取目標電磁散射特性的眾多方法中，動態測量由于處于實際復雜環境因而獲取的數據具備更高的可信度和應用價值。仿真與實測RCS數據的相似度成為衡量計算機電磁仿真能力的主要指標。在動態測量環境中，運動目標由于受到各類復雜因素的影響，其實際姿態與通過測量或計算得到的目標預估姿態通常存在一定程度差異。鑒于復雜目標RCS的姿態敏感性較高，姿態差異成為RCS數據誤差的主要來源之一。對目標實際和預估姿態之間的差異進行計算機建模可有效提升計算機的電磁仿真能力，為RCS數據的一致性評估提供有價值的參考信息。

運動目標實際和預估姿態之間的差異可分為兩類，一類稱為姿態微動，通常由目標自身幾何形態以及重力影響導致，可用確定性的數學模型進行描述［1-2］；另一類統稱為姿態擾動，通常由大氣湍流、海浪起伏、姿態測量與計算以及人工操作誤差等因素造成，這些因素較難用確定性的數學模型進行描述且具備很大的隨機性，使得姿態擾動的分布形式同樣非常復雜且不可預估。

鑒于姿態對于目標RCS評估的重要性，研究人員對目標靜動態測量情況下的姿態一致性展開了研究［3-4］。通過建立靜動態條件下不同坐標系之間的轉換關系實現了動態雷達目標仿真中的姿態角計算［5］，分析了姿態不確定性對于動態測量RCS的影響［6］，并從RCS統計分布特性以及測量不確定性等方面對靜動態RCS差異進行討論［78］。這些工作主要針對靜動態測量條件下目標姿態的一致性展開探討，對RCS數據的評估偏向于統計模型分布上的差異。由于實驗條件的限制，采用測量手段無法對姿態擾動導致的目標動態RCS差異分布特性進行專門研究。姿態擾動模型的缺乏則成為了計算機仿真的主要難點，現有公開發表的資料中僅有文獻［9］對運動目標姿態擾動進行了建模，采用該模型的目標動態RCS仿真局限于初步的分析和討論［10-11］。

本文以圖形電磁計算（graphical electromagnetic computing，GRECO）［1213］為仿真平臺研究了姿態擾動對于目標動態RCS分布特性的影響。利用GRECO運算速度快的特點，將其與蒙特卡羅仿真方法相結合構建了具備姿態擾動仿真功能的目標動態RCS仿真平臺。在原有的動目標RCS仿真平臺的基礎上，采用均勻分布的隨機模型對目標在方位、俯仰和側滾平面上的姿態角擾動進行了建模，將擾動變量添加到原有的動態目標姿態角序列中，應用蒙特卡羅仿真獲取大量姿態擾動情況下目標的動態RCS序列。采用統計分析的方法研究了似靜和擾動狀態下目標動態RCS差異的分布特性，提出了動態RCS置信區間以及數學期望值的計算方法，將所得結果與某擾動模型情況下的動態RCS進行比對評估。實驗結果表明該方法物理意義清晰，具備較強的可操作性和工程應用價值，且易于擴展至對其他誤差因素的仿真分析，為運動目標RCS的測量與仿真數據一致性評估提供了有價值的研究方法和參考信息。

1 運動目標的姿態角解算方法

目標動態RCS的計算機仿真通常采用“似靜法”，即將目標運動軌跡離散化為若干采樣點，動態RCS序列由采樣點上的若干RCS值組成。在GRECO仿真平臺中，目標在雷達視角中的姿態是計算RCS的關鍵參數。姿態解算通常是以建立雷達坐標系、目標坐標系以及二者之間的轉換關系來實現的。雷達坐標系是以雷達自身所在位置為目標坐標系的原點，XOY平面通常用于描述水平面，Z軸表示目標在雷達坐標系中的高度，如圖1（a）所示。α（t）為目標在XOY平面的投影點與X軸正方向夾角（方位角），β（t）為目標與Z軸正方向夾角（俯仰角），R（t）為目標和雷達之間的距離，t為時間或采樣單位［14］，這3個參數可以換算成目標在雷達坐標系中的坐標。目標坐標系采用目標的幾何中心作為原點，通常采用方位、俯仰和側滾3個角進行描述，其定義如圖1（b）所示，分別用符號φ（t），θ（t）和γ（t）表示，其指向由右手法則確定。

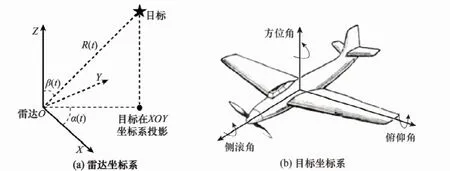
圖1 姿態角解算坐標系示意圖

雷達坐標系與目標坐標系的轉換關系為

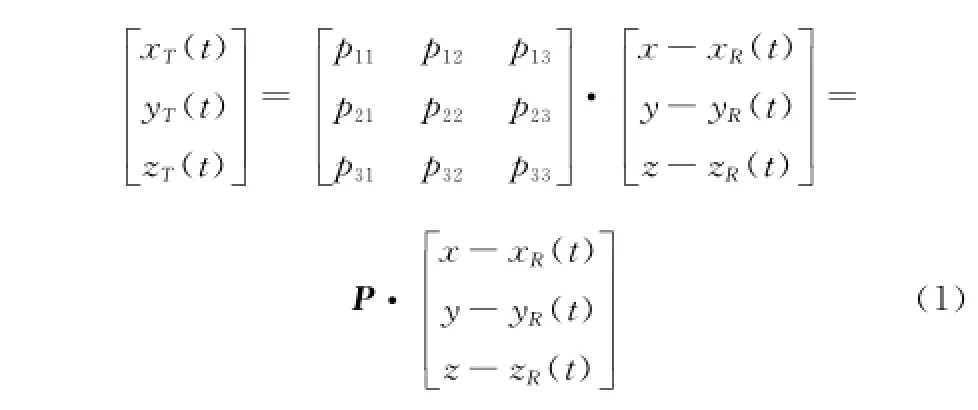
式中，（x，y，z）為雷達坐標系中任意一點的坐標；（xR（t），yR（t），zR（t））為目標點在雷達坐標系中的坐標；（xT（t），yT（t），zT（t））為點（x，y，z）在目標坐標系中的坐標；P為從雷達坐標系到目標坐標系的變換矩陣，其中元素定義分別為

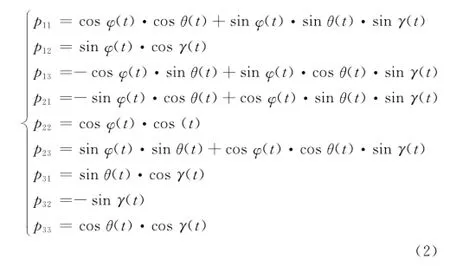
將雷達坐標（0，0，0）代入式（1）中即可計算出雷達在目標坐標系中的位置。

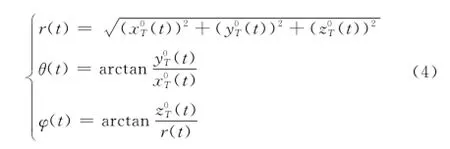
2 基于GRECO和蒙特卡羅仿真方法的動目標RCS仿真分析平臺

上述姿態解算方法所得結果為目標的預估姿態，尚未考慮姿態擾動的影響，因而也可稱為“似靜”姿態。如前所述，由于實際復雜環境中各種因素的影響，目標的“似靜”姿態通常與實際姿態存在差異。研究姿態擾動對于動目標RCS的影響需要通過在“似靜”姿態中添加姿態擾動量來實現。姿態擾動的復雜性和不可預估性使得采用隨機模型對其進行建模是比較合理的選擇。隨機模型的分布形式對于目標動態RCS的分布特性有較大影響，也是本文建立的仿真平臺中的關鍵問題。現有公開發表的文獻資料中僅有文獻［9］中介紹了一種姿態擾動模型，然而該模型并不能涵蓋實際環境中的全部姿態擾動分布形式，所得結論存在局限性。若將目標動態RCS的姿態角擾動響應特性看作目標電磁散射特性的一個系統函數V＝F（u），其中u為姿態擾動模型，則“平整”的均勻分布隨機模型u可以更好地反映出目標動態RCS對于姿態擾動響應的本質特征，所得結論也更具備普適性。鑒于此，本文采用均勻分布的隨機模型對姿態擾動進行建模。由于選擇了隨機模型作為目標RCS姿態擾動響應的輸入參數，因而將GRECO與蒙特卡羅仿真相結合就成為了一種可行的技術路線。

將3個相互獨立的均勻分布隨機變量分別添加到“似靜”狀態下目標的方位、俯仰和側滾角中，目標的姿態角序列變為

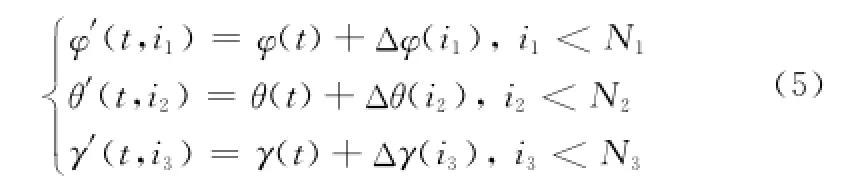
式中，φ′表示添加擾動元素后的目標姿態角；φ為“似靜”狀態下的目標姿態角；t＝｛1，2，…，T｝表示運動序列中的采樣點；Ni表示在3個姿態角平面上姿態角隨機擾動量的個數。本文假設姿態角在三個平面上的擾動為相互獨立，因而為保證蒙特卡羅仿真的全面性，仿真次數N要滿足N≥N1·N2·N3。式（5）表明，考慮姿態擾動因素后采樣點t的目標姿態由“似靜”狀態下的一組（φ（t），θ（t），γ（t））變為擾動情況下的N組（φ′（t，i1），θ′（t，i2），γ′（t，i3）），對應的RCS序列也從σ（t）變為了σ′（t，i） （i＝｛1，2，…，N｝）。從而可以圍繞“似靜”和擾動狀態下RCS序列的差異分布來研究姿態擾動對目標動態RCS的影響。整個仿真平臺的流程圖如圖2所示。

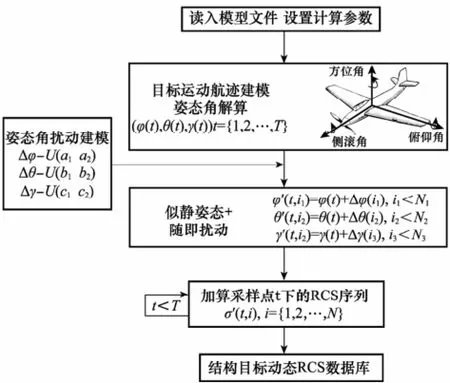
圖2 姿態擾動下目標動態RCS仿真流程圖

圖3 為采用該平臺獲取的直線運動航跡中某采樣點下飛機目標“似靜”與姿態擾動RCS差異Δσ的統計直方圖，頻率分別為3 GHz和10 GHz。由于復雜目標RCS的姿態敏感性與頻率成正比，10 GHz下的統計直方圖相比較3 GHz更佳扁平，表明姿態擾動在較高頻率下對RCS影響更大。鑒于該直方圖分布與正態分布的相似性，本文選取了χ2分布擬合檢驗對Δσ的分布特性進行了進一步的驗證［15］，結果表明兩個頻率下的直方圖分布均符合錯誤概率為5%的檢驗顯著性水平，驗證了Δσ符合正態分布的假設，且錯誤概率與雷達波頻率成反比，這一現象可用中心極限定理進行解釋。

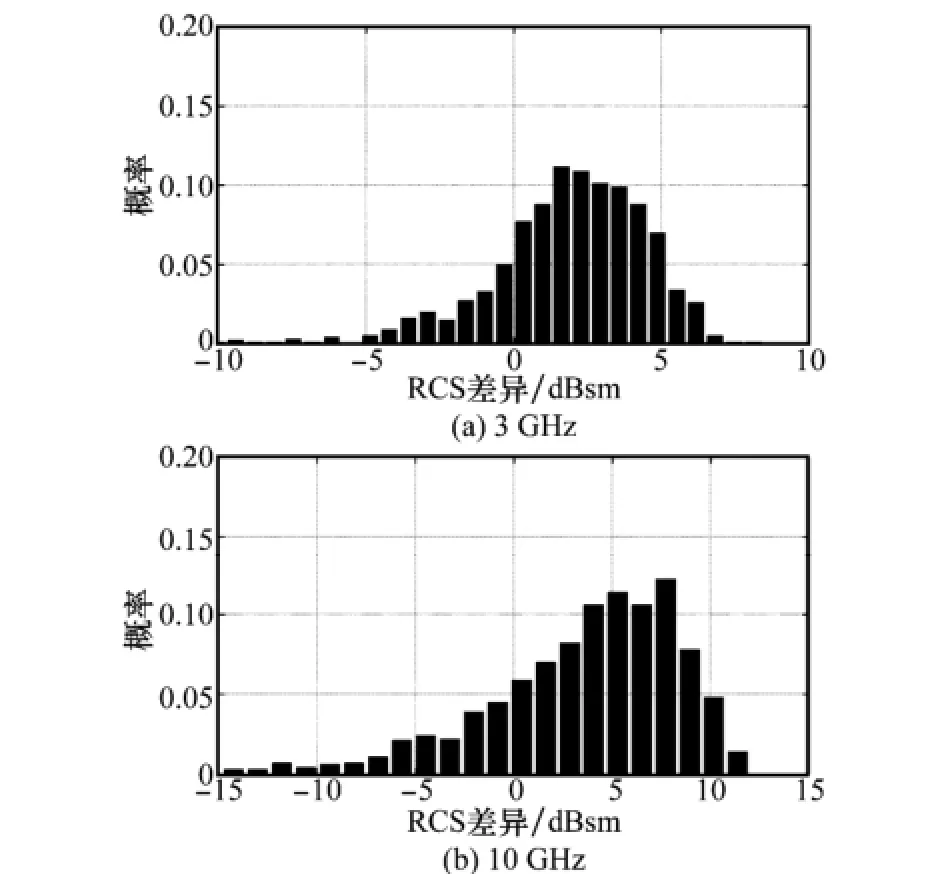
圖3 運動航跡某采樣點下RCS差異統計直方圖

Δσ直方圖與正態分布的高相似度使得均值和標準差可有效描述靜動態RCS差異的分布形式，然而這兩個統計量并不適用于直觀描述姿態不確定性對整個動態RCS序列的影響。通過對各類目標在不同姿態下的Δσ分布進行分析后發現，其直方圖的分布形式在大部分情況下均屬于中間高兩邊低的準對稱結構。這使得采用比統計量更加直觀的方法描述動態RCS分布特性成為可能。圖4為上述運動航跡中采樣點t的Δσ統計直方圖，其分布形式具備代表性。

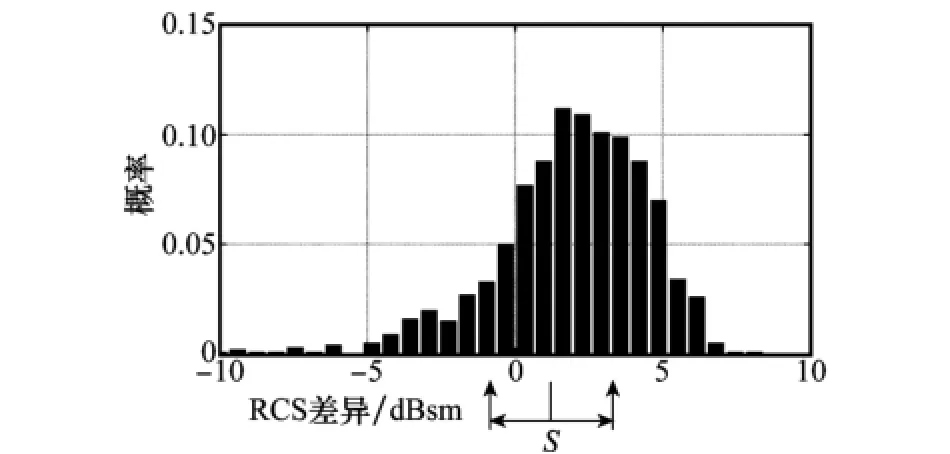
圖4 直方圖遍歷以及置信區間計算示意圖

本文提出的RCS置信區間正是以該直方圖的分布特性為基礎進行計算。具體步驟如下：

步驟1 定義概率門限參數a作為置信區間搜索的終止條件。

步驟2 以直方圖中概率最大點對應位置作為計算機程序遍歷的起始點，定義為s；設置兩個變量分別沿直方圖的正負方向進行遍歷。如圖4中兩個箭頭所示。

步驟3在遍歷Δσ直方圖的同時，計算遍歷的積累概率c，即圖4中兩個箭頭之間直方圖所對應的概率之和為

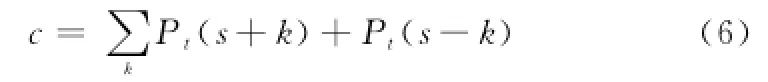
步驟4 當積累概率大于概率門限a時，遍歷程序終止，程序終止時正負兩個方向上的箭頭所對應的Δσ值與似靜狀態下的RCS值之和為采樣點t對應的置信區間上限U（t）和下限L（t）。

步驟5 對整條運動航跡下每個采樣點采用相同的方法計算其置信區間的上限和下限，獲取動態RCS的置信區間序列U和L。

圖5所示為目標動態RCS置信區間仿真的整體流程圖。該置信區間的物理意義是：在目標當前的運動條件下，姿態擾動使得目標動態RCS在L（t）和U（t）之間分布的概率為a。其數學形式為

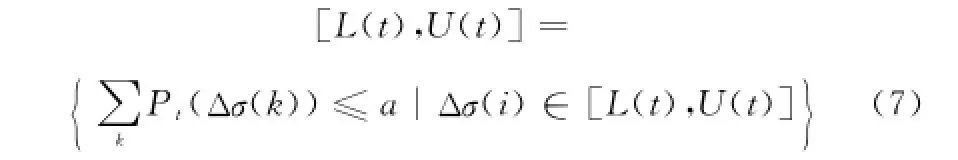
置信區間的概念直觀描述了姿態擾動對目標動態RCS分布的影響，物理意義清晰，適用于研究不同條件下的靜動態RCS差異分布。然而在某些應用環境下用單一精確數值來表征姿態擾動情況下目標動態RCS更有利于靜動態數據的一致性評估。對蒙特卡羅仿真所得全部擾動RCS求平均值的方法并不能有效體現出RCS的統計分布信息，鑒于此，本文采用數學期望值作為擾動RCS的最佳數值表示。其計算公式為

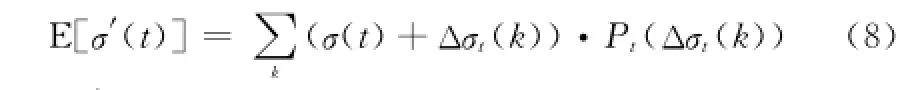
式中，E［σ′（t）］表示在姿態擾動情況下運動序列采樣點t的RCS期望值；σ（t）為“似靜”狀態下采樣點t的RCS值；Δσt為該采樣點下擾動與“似靜”狀態下RCS的差異分布值；Pt（Δσt（k））為直方圖中所對應的概率值。

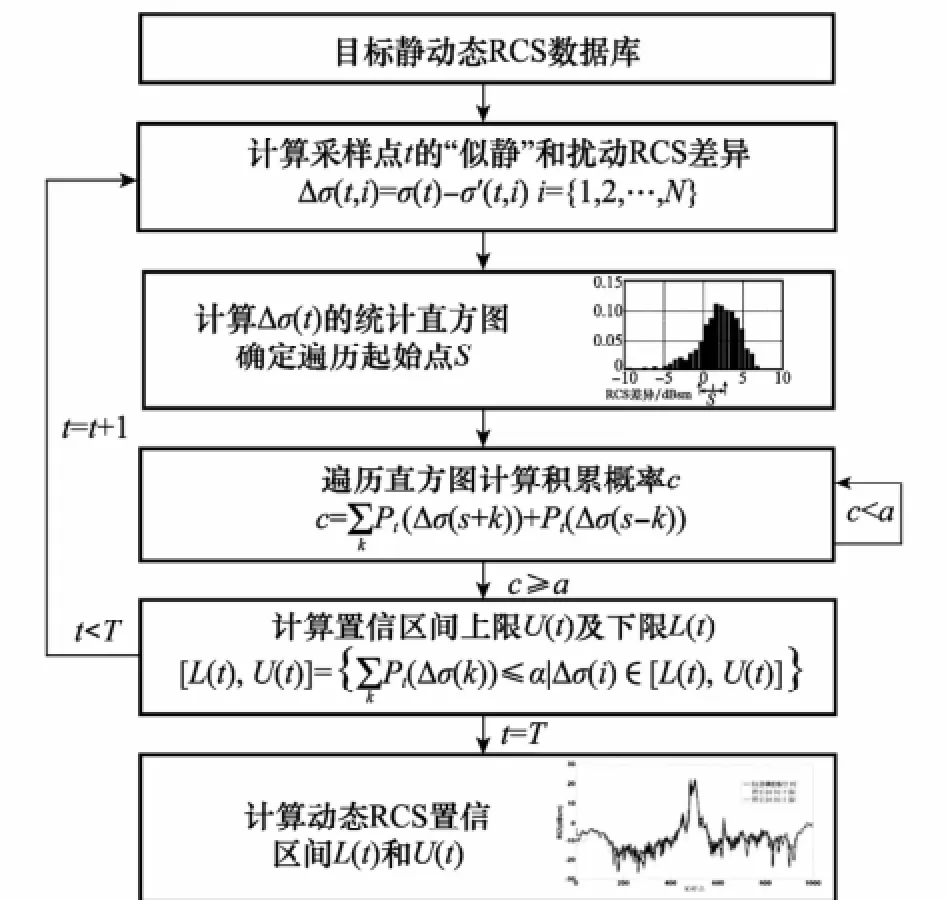
圖5 動態RCS置信區間計算流程圖

3 實驗結果與分析

本文選擇飛機作為動態RCS仿真的幾何模型對所提方法進行驗證。飛機的運動模式分為兩類，一類為沿直線航跡飛行，航跡起始點和終止點坐標分別為（－10 000，800，1 000）和（10 000，700，1 000），雷達位于坐標系的原點，所有單位均為m。航跡采樣點個數為1 000，均勻分布于整條飛行航跡上。雷達頻率為10 GHz，極化方式為垂直發射垂直接收（vertical transmitting and vertical receiving，VV）極化。飛機在方位、俯仰和側滾平面上的擾動分布形式服從均勻分布，擾動范圍（－1°，1°），蒙特卡羅仿真次數為106。另一類運動模式為曲線飛行，飛行軌跡在地面投影如圖6所示，飛行高度在2 000～3 000 m之間不均勻變化，雷達位于坐標系原點。運動軌跡采樣點個數為800，雷達波頻率為2．5 GHz，極化方式為水平發射水平接收（horizontal transmitting and horizontal receiving，HH）極化。姿態擾動模型與直線運動模式一致。

圖6 曲線運動軌跡水平面投影示意圖

（1）動態RCS置信區間分布

圖7所示為兩種運動模式下飛機動態RCS置信區間以及“似靜”狀態下的RCS分布，概率門限均為80%。從圖7中可以看出，大部分“似靜”狀態下的RCS值被包裹在置信區間的上限和下限之間，運動序列各采樣點之間的RCS置信區間上下限差異分布不均勻，說明不同姿態下目標RCS的姿態敏感性存在差別。置信區間的下限并不一定小于“似靜”狀態下的RCS值，而其上限同樣也不一定大于“似靜”RCS值，其分布與Δσ統計直方圖的形狀和值域分布有很大關聯。

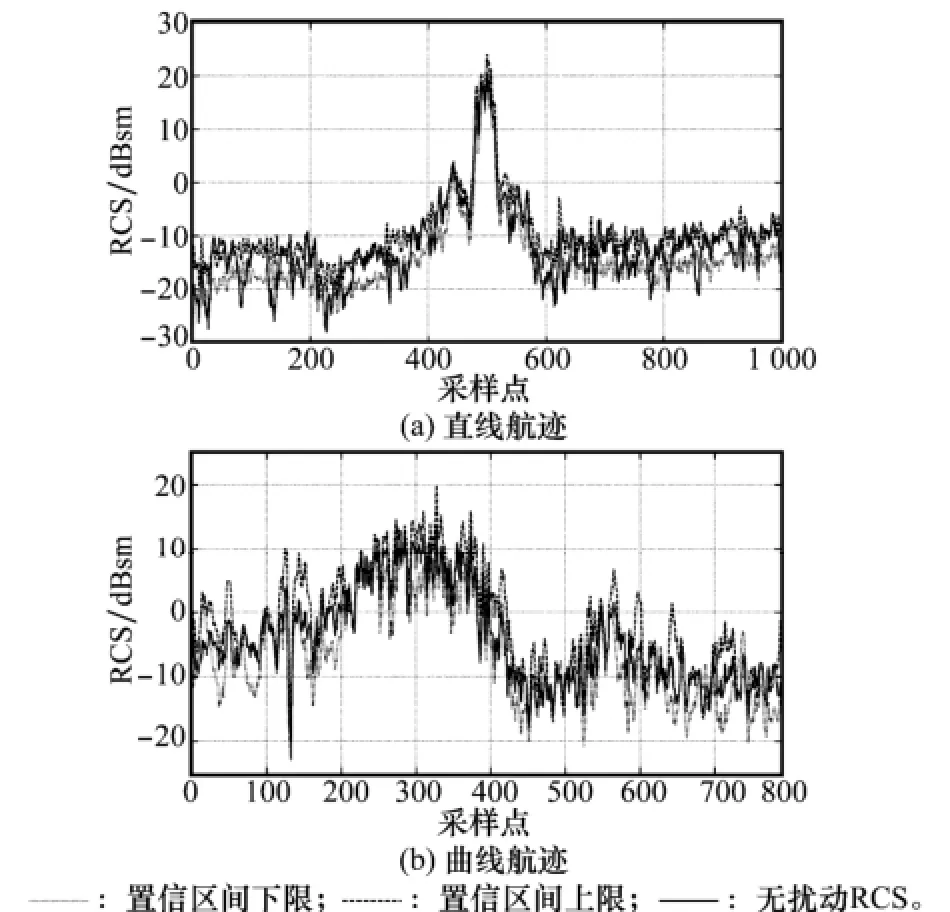
圖7 飛機目標動態RCS置信區間分布圖

（2）文獻［9］擾動模型下動態RCS的比對驗證

飛機目標在實際運動過程中的姿態擾動并非嚴格服從均勻分布，因而圖7所示的RCS置信區間并非目標動態RCS的真實分布。為了對置信區間及期望值的實用性進行驗證，本文選取了文獻［9］介紹的擾動模型對兩種運動模式下的目標動態RCS進行了仿真計算。該擾動模型在方位和俯仰平面上的擾動方差均為1°，側滾角擾動服從（－1°，1°）之間的均勻分布，取樣間隔為1個采樣點，擾動周期為8個采樣點，動態RCS置信區間計算中采用的擾動模型在3個平面上服從（－1°，1°）范圍內的均勻分布。圖8為兩種運動模式下采用該擾動模型得到的動態RCS與置信區間的分布比對。在直線運動軌跡中，采用文獻［9］中擾動模型計算的動態RCS值大部分位于置信區間的上限和下限之間，經統計所占比例達到86．1%；在曲線航跡中這一數值為74．12%。當置信區間的概率門限參數從80%增加至90%后，擾動RCS位于置信區間上下限之間的比例在兩種運動模式下分別達到88．2%和78%。上述數據表明在姿態擾動范圍一致或近似的情況下，動態RCS置信區間可以較好地“包裹”住實際擾動情況下的動態RCS值。這一現象也從另一個角度詮釋了其物理概念，即置信區間并不代表目標動態RCS的真實分布，而是提供了一個動態RCS最有可能的分布范圍，這一可能的精確數值可用計算置信區間的門限概率表征。

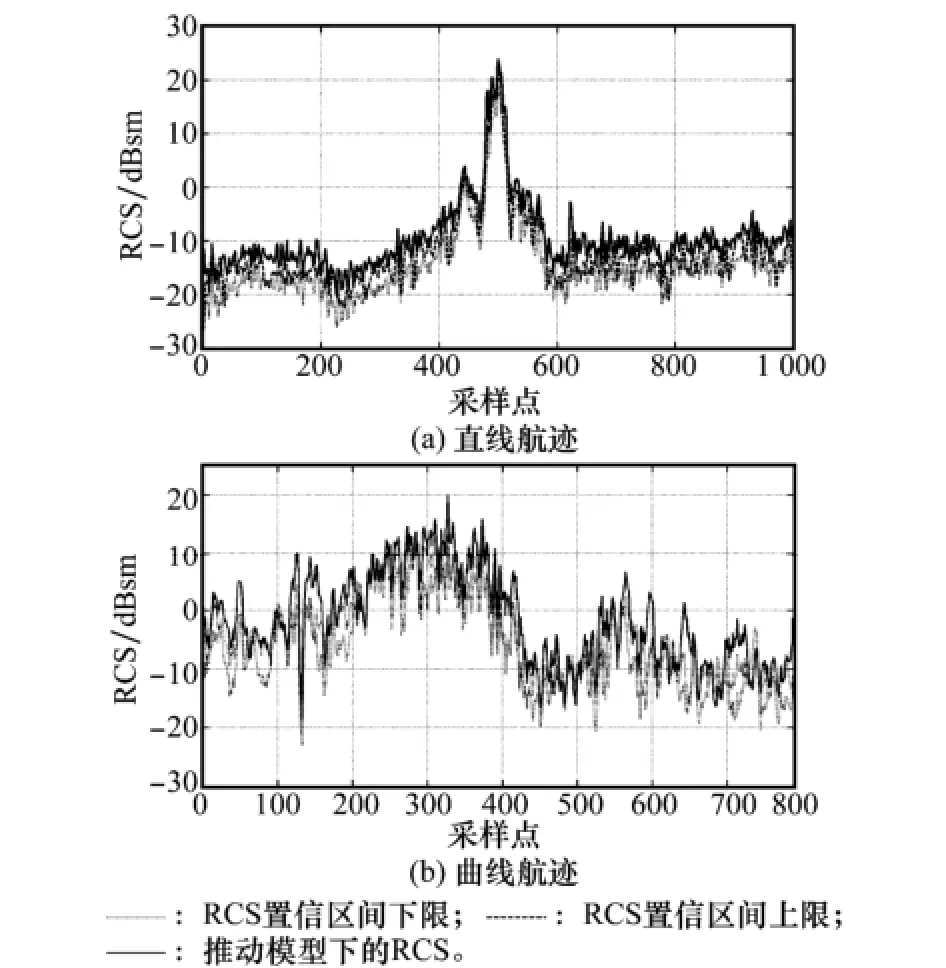
圖8 采用文獻［9］中模型的動態RCS與置信區間比對

圖9 為采用本文提出的期望值計算方法獲取的直線運動模式下動態RCS期望值與圖8（a）中擾動RCS值的直接比對，兩組數據差異的均值為2．68 dBsm，采用文獻［16- 17］中介紹的FSV方法對兩組數據進行定量評估，其相似度為82．74%。曲線運動模式下對應的擾動RCS值與期望值的特征選擇驗證（feature selective validation，FSV）相似度為77．49%。姿態擾動模型的分布形式通常對其RCS的數學期望值有較大影響，因而可采用不同擾動模型的RCS期望值與實際擾動RCS進行一致性評估，從而實現對目標姿態擾動模型的反演。

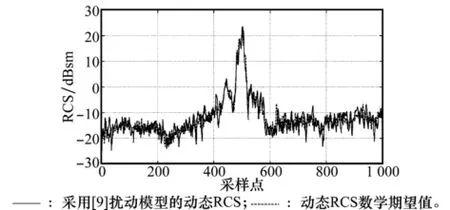
圖9 采用［9］中模型的動態RCS與期望值比對

（3）RCS置信區間的擴展應用

置信區間的概念可以反映出目標RCS在姿態擾動情況下分布本質特征，這對于目標RCS特征庫的構建具有重要指導意義。圖10為某飛機模型在水平面0°～180°范圍內的RCS置信區間分布，其中0°為飛機正對雷達方向。姿態擾動服從均勻分布，擾動范圍在－2°～2°之間，頻率分別為3 GHz和10 GHz。可以看出10 GHz下RCS置信區間的值域分布范圍要大于3 GHz，表明其姿態敏感性更高，這與目標RCS的姿態敏感性是一致的。從圖10中也可以觀察到該目標在方位角0°以及180°左右的范圍內對于姿態擾動的敏感性不高，似靜與置信區間的RCS值差異不明顯，而在目標正側視以及斜側視的姿態范圍內，姿態擾動所造成的靜動態RCS差異較大，在實際應用中可根據這一特性適當調整雷達參數從而提高目標的識別率，而對于目標RCS特征庫的建立以及不同數據源的一致性評估也提供了有價值的參考信息。

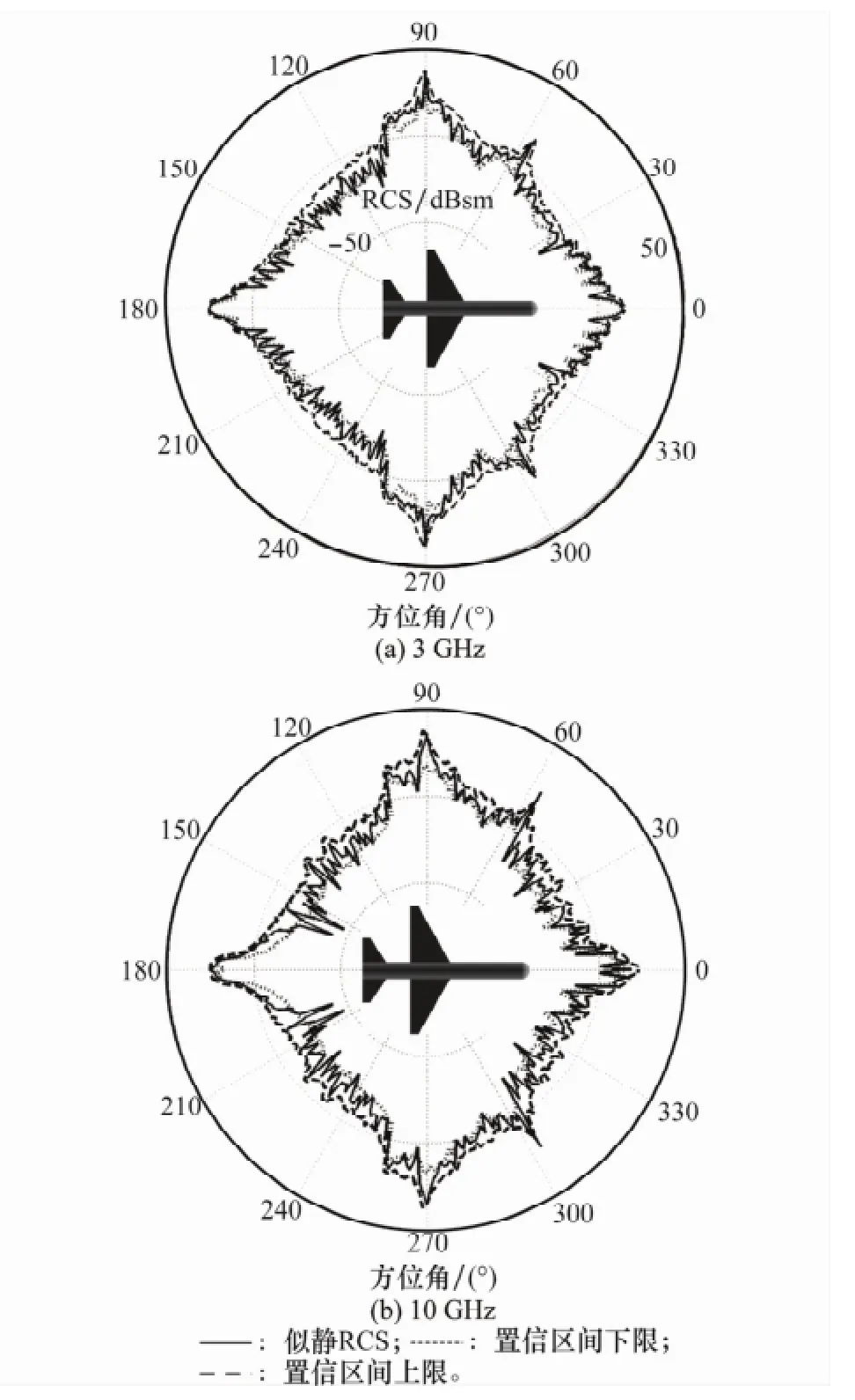
圖10 飛機模型水平面RCS置信區間分布

4 結 論

目標在運動過程中由于各種復雜因素的影響，其實際姿態往往與通過測量或計算得到的預估姿態存在差異，主要表現為姿態的擾動。姿態擾動是靜動態測量與仿真RCS數據的主要誤差源之一。本文構建了GRECO和蒙特卡羅仿真為基礎的動目標RCS仿真分析平臺，對姿態擾動情況下目標動態RCS分布特性進行了研究。采用均勻分布隨機模型對目標在方位、俯仰和側滾平面上的姿態擾動進行建模，將“似靜”與擾動狀態下的RCS數據差異進行統計分析，結合直方圖的分布特點提出了動態RCS置信區間以及數學期望值的計算方法。本文選擇兩種運動模式的飛機目標對該方法進行驗證，將其動態RCS置信區間和期望值與現有文獻資料中介紹的擾動模型動態RCS進行比對評估。實驗結果表明該方法物理意義清晰，具備較強的可操作性和工程應用價值，為靜動態RCS數據的一致性評估以及特征庫的構建提供了有價值的參考信息和分析手段，并可擴展至對其他誤差因素的建模分析，進一步提升計算機的電磁仿真能力。

［1］Li Y，Du L，Liu H．Hierarchical classification of moving vehicles based on empirical mode decomposition of micro-Doppler signatures［J］．IEEE Trans.on Geoscience and Remote Sensing，2013，51（5）：3001- 3013．

［2］Wang J，Lei P，Sun J P，et al．Spectral characteristics of mixed micro-Doppler time-frequency data sequences in micro-motion and inertial parameter estimation of radar targets［J］．IET Radar，Sonar&Navigation，2014，8（4）：275- 281．

［3］Li J L，Zeng Y H，Zhou B，et al．Gesture consistency of airplane target between static and dynamic measurements［J］．Journal of Beijing University of Aeronautics and Astronautics，2013，39（4）：453- 457．（李金梁，曾勇虎，周波，等．飛機目標靜態與動態測量的姿態一致性［J］．北京航空航天大學學報，2013，39（4）：453- 457．）

［4］Dai C，Xu Z H，Xiao S P．Analysis for differences between dynamic and static RCS characteristics of radar target［J］．Journal of Signal Processing，2013，29（9）：1256- 1263．（戴崇，徐振海，肖順平．雷達目標動靜態RCS特性差異分析［J］．信號處理，2013，29（9）：1256- 1263．）

［5］Liu Y Z，Zeng Y H，Wang L D，et al．Calculation of attitude angle in dynamic radar target simulation［J］．Electronics Optics and Control，2007（1）：38- 41．（劉英芝，曾勇虎，汪連棟，等．動態雷達目標仿真中目標姿態角的計算［J］．電光與控制，2007（1）：38- 41．）

［6］Jiang W D，Cao M，Nie L，et al．Study on dynamic electromagnetic data simulation of space targets［J］．Systems Engineering and Electronics，2009，31（9）：2042- 2045．（姜衛東，曹敏，聶鐳，等．空間目標動態電磁測量數據仿真方法研究［J］．系統工程與電子技術，2009，31（9）：2042- 2045．）

［7］Wu Y P，Lei Z Y，Shan T B．Study of the effect of target pose on RCS dynamic measurement［J］．Electronic Science and Technology，2011，24（4）：40- 42．（吳永鵬，雷振亞，山團彪．目標姿態對RCS動態測量影響的研究［J］．電子科技，2011，24（4）：40- 42．）

［8］Zeng Y H，Wang G Y，Chen Y G，et al．Statistical analysis for RCS of dynamic radar target［J］．Chinese Journal of Radio Science，2007，22（4）：610- 613．（曾勇虎，王國玉，陳永光，等．動態雷達目標RCS的統計分析［J］．電波科學學報，2007，22（4）：610- 613．）

［9］Luo H．The study on the identification and recognition of moving radar targets［D］．Beijing：The Second Research Academic，China Aerospace Science and Industry Corporation，1999．（羅宏．動態雷達目標的建模與識別研究［D］．北京：航天工業總公司第二研究院，1999．）

［10］Su D L，Zeng G Q，Liu Y，et al．RCS study of moving radar targets［J］．Journal of Beijing University of Aeronautics and Astronautics，2006，32（12）：1413- 1417．（蘇東林，曾國奇，劉焱，等．運動目標RCS特性分析［J］．北京航空航天大學學報，2006，32（12）：1413- 1417．）

［11］Fang X，Su D L．Prediction of in-flight aircraft radar cross-section［C］∥Proc.of the International Symposium on Antennas，Propagation and EM Theory，2008：526- 529．

［12］Liu J，Fang N，Wang B F，et al．An Efficient ray-tracing method for RCS prediction in GRECO［J］．Microwave and Optical Technology Letters，2013，55（3）：586- 589．

［13］Cheng Z H，Xie Y J，Fan J．Fast computation of near field RCS of complex objects in terahertz band［J］．Journal of Electronics&Information Technology，2014，36（8）：1999- 2004．（程志華，謝擁軍，樊君．復雜目標的太赫茲波近場RCS快速計算［J］．電子與信息學報，2014，36（8）：1999- 2004．）

［14］Huang P K，Yin H C，Xu X J．Radar target characteristic［M］．Beijing：Publishing House of Electronics Industry，2005：195- 219．（黃培康，殷紅成，許小劍．雷達目標特性［M］．北京：電子工業出版社，2005：195- 219．）

［15］Eberhard Z，Wolfgang H，Schwarz H．Teubner-taschenbuch der mathematik［M］．Beijing：Science Press，2012：1025- 1027．（Eberhard Z，Wolfgang H，Schwarz H．數學指南 實用數學手冊［M］．北京：科學出版社，2012：1025- 1027．）

［16］Martin A J M．Quantitative data validation-automated visual evaluations［D］．Leicester：De Montfort University，1999．

［17］Duffy A P，Martin A J M，Orlandi A，et al．Feature selective validation（FSV）for validation of computational electromagnetics（CEM）：part I-the FSV method［J］．IEEE Trans.on Electromagnetic Compatibility，2006，48（3）：449- 459．

Dynamic target RCS characteristic analysis under the influence of attitude perturbation

LIU Jia，FANG Ning，XIE Yong-jun，WANG Bao-fa
（School of Electronic and Information Engineering，Beihang University，Beijing 100191，China）

Attitude perturbation of the dynamic radar target is the major cause in radar cross section（RCS）differences between static and dynamic systems．The perturbation factors are usually complicated and unpredictable，which aggravate the difficulty of target dynamic RCS characteristic research．A simulation platform based on the combination of graphical electromagnetic computing（GRECO）and Monte Carlo simulation methods is proposed，which uses random variables with uniform distribution to model the attitude perturbation．The concept and computation methods of dynamic RCS credibility zone and expected value are demonstrated according to the pattern of RCS differences between quasi-static and perturbed attitudes．The aircraft with two kinds of motion models is taken to validate the proposed platform．Simulation results are compared with the one from the practical attitude perturbation model．Conclusions validate the feasibility of the proposed method，which enhances the simulation capability of GRECO and provides the effective solution to the target electromagnetic scattering cha-racteristic data consistency evaluation in addition to the attitude sensitivity analysis．

radar cross section（RCS）；graphical electromagnetic computing（GRECO）；dynamic simulation；Monte Carlo simulation

TN 95

A

10．3969／j．issn．1001-506X．2015．04．09

劉 佳（1985-），男，博士，主要研究方向為電磁散射與目標特性。E-mail：bobmp5＠163．com

方 寧（1979-），女，講師，博士，主要研究方向為電磁散射與逆散射，目標識別。E-mail：fangn31＠163．com

謝擁軍（1968-），男，教授，博士，主要研究方向為計算微波與計算電磁學、天線與微波工程。E-mail：yjxie＠buaa．edu．cn

王寶發（1938-），男，教授，主要研究方向為電磁散射與逆散射、目標識別、天線與微波工程。E-mail：b．f．wang＠163．com

1001-506X（2015）04-0775-07

2014- 06- 11；

2014- 09- 22；網絡優先出版日期：2014- 10- 30。

網絡優先出版地址：http：／／w ww．cnki．net／kcms／detail／11．2422．TN．20141030．1010．008．html