高考中的動力學題型

張建生

高考物理的幾大題型在2014年高考中主要表現在平衡問題、臨界問題、守恒問題、復合場問題、多過程問題、圖象問題等基本題型方面.

一、平衡問題

共點力作用下物體的平衡條件是靜力學的基礎，主要考查學生的基礎知識和基本能力，題型以選擇題為主，難度適中，也要注意與電磁學的綜合應用.

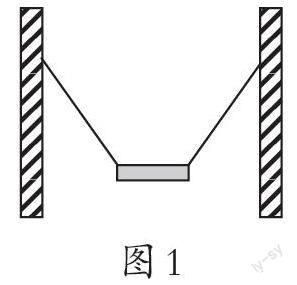
例1 ?（2014年高考山東卷）如圖1所示，用兩根等長輕繩將木板懸掛在豎直木樁上等高的兩點，制成一簡易秋千.某次維修時將兩輕繩各剪去一小段，但仍保持等長且懸掛點不變.木板靜止時，[F1]表示木板所受合力的大小，[F2]表示單根輕繩對木板拉力的大小，則維修后（ ? ） [ 圖1]

A.[F1]不變，[F2]變大

B.[F1]不變，[F2]變小

C.[F1]變大，[F2]變大

D.[F1]變小，[F2]變小

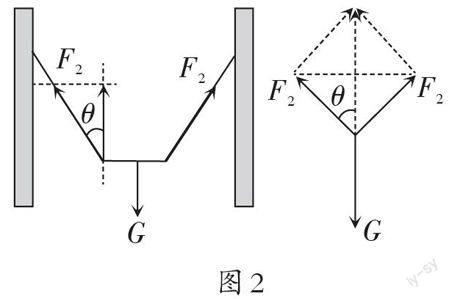
解析 ?考查受力分析、物體的平衡.在輕繩被剪短前后，木板都處于靜止狀態，所以木板所受的合力都為零，即[F1]=0.因兩根輕繩等長，且懸掛點等高，故兩根輕繩對木板的拉力相等，均為[F2].對木板進行受力分析，如圖2所示，則豎直方向根據平衡方程，有[2F2cosθ=G]. 輕繩剪去一段后，[θ]增大，cos[θ]減小，故[F2]變大.選項A正確. 選A項. [ 圖2]

點撥 ?解平衡問題的關鍵在于正確進行受力分析和對力的處理. 動態平衡問題可考慮圖解法和解析法.

二、臨界問題

當物體從某種特性變化到另一種特性時，發生質的飛躍的轉折狀態通常叫臨界狀態. 出現臨界狀態時，可理解為“恰好出現”，也可以理解為“恰好不出現”的物理現象.

例2 ?（2014年高考四川卷）如圖3所示，水平放置的不帶電的平行金屬板[p]和[b]相距[h]，與圖示電路相連，金屬板厚度不計，忽略邊緣效應.[p]板上表面光滑，涂有絕緣層，其上[O]點右側相距[h]處有小孔[K];[b]板上有小孔[T]，且[O、T]在同一條豎直線上，圖示平面為豎直平面.質量為[m]、電荷量為[-q（q>0）]的靜止粒子被發射裝置（圖中未畫出）從[O]點發射，沿[p]板上表面運動時間[t]后到達[K]孔，不與板碰撞地進入兩板之間.粒子視為質點，在圖示平面內運動，電荷量保持不變，不計空氣阻力，重力加速度大小為[g].

[圖3]

（1）求發射裝置對粒子做的功;

（2）電路中的直流電源內阻為[r]，開關S接“1”位置時，進入板間的粒子落在[b]板上的[A]點，[A]點與過[K]孔豎直線的距離為[l]. 此后將開關S接“2”位置，求阻值為[R]的電阻中的電流強度.

解析 ?（1）設粒子在[p]板上做勻速直線運動的速度為[v0]，有[h=v0t]①

設發射裝置對粒子做的功為[W]，由動能定理，有

[W=12mv20]②

聯立①②可得[W=mh22t2]③

（2）S接“1”位置時，電源的電動勢[E0]與板間電勢差[U]，有[E0=U]④

板間產生勻強電場的場強為[E]，粒子進入板間時有水平方向的速度[v0]，在板間受到豎直方向的重力和電場力作用而做類平拋運動. 設加速度為[a]，運動時間為[t1]，有

[U=Eh]⑤ [mg-qE=ma]⑥ [h=12gt21]⑦ [l=v0t1]⑧

S接“2”位置，則在電阻[R]上流過的電流[I]滿足

[I=E0R+r]⑨

聯立①④～⑨得[I=mh（R+r）（g-2h3l2t2）]⑩

點撥 動力學中常見的臨界問題主要有兩類：一是彈力發生突變時接觸物體間的脫離與不脫離，繩子的繃緊與松弛問題;二是摩擦力發生突變時滑動與不滑動問題，外力變化導致靜摩擦力為零并改變方向的問題. 處理這類問題的關鍵是：（1）通過物理過程的分析，找出臨界狀態. （2）抓住處于臨界狀態時物體的受力、運動狀態的特征，找出臨界條件.

三、守恒問題

守恒問題貫穿整個高中物理，它既是一條重要的規律，同時也是研究物理問題的重要思維方法，如機械能守恒、能量守恒、動量守恒、電荷守恒、質量數守恒等.

例3 （2014年高考福建卷）圖4為某游樂場內水上滑梯軌道示意圖. 整個軌道在同一豎直平面內，表面粗糙的[AB]段軌道與四分之一光滑圓弧軌道BC在B點水平相切.點A距水面的高度為H，圓弧軌道BC的半徑為R，圓心O恰在水面.一質量為m的游客（視為質點）可從軌道AB的任意位置滑下，不計空氣阻力. [ 圖4]

（1）若游客從A點由靜止開始滑下，到B點時沿切線方向滑離軌道落在水面上的D點，OD=2R，求游客滑到B點時的速度vB大小及運動過程軌道摩擦力對其所做的功Wf;

（2）若游客從AB段某處滑下，恰好停在B點，又因受到微小擾動，繼續沿圓弧軌道滑到P點后滑離軌道，求P點離水面的高度h.

解析 ?（1）游客從[B]點做平拋運動，有

[2R=vBt]① ?[R=12gt2]②

由①②式得[vB=2gR]③

從[A]到[B]，根據動能定理，有

[mg（H-R）+Wf=12mv2B-0]④

由③④式得[Wf=-（mgH-2mgR）]⑤

（2）設[OP]與[OB]間夾角為[θ]，游客在[P]點時的速度為[vP]，受到的支持力為[N]，從[B]到[P]由機械能守恒定律，有[mg（R-Rcosθ）]=[12mv2P]-0 ⑥

過[P]點時，根據向心力公式，有

[mgcosθ-N=][mv2PR]⑦ ?[N=0]⑧ ?cos[θ]=[hR]⑨

由⑥⑦⑧⑨式解得[h=23R] ⑩

點撥 ?對于能量守恒問題（包括機械能守恒），找出研究過程中各種形式的能量的變化是解題的關鍵.