基于博弈論的無線傳感網絡DDoS攻擊防御優化策略

徐翔　沈士根　曹奇英

摘 要：如何有效優化現有無線傳感器網絡中DoS/DDoS攻擊的防御策略是當前的研究熱點問題之一。本文結合目前無線傳感器網絡中的防御技術，利用博弈論的方法建立模型。該模型通過優化防火墻閥值和針對攻擊節點給予懲罰措施的方法，來降低攻擊節點的收益，使理性攻擊者放棄攻擊，從而達到了有效防御DoS/DDoS攻擊的目的。最后實驗通過比較現有的防御策略與提出的優化策略，驗證了該防御優化策略的有效性，從而達到了防御DoS/DDoS攻擊的目的。

關鍵詞：無線傳感器網絡；DoS/DDoS攻擊；博弈論；防御策略優化

中圖分類號：TP393.0 文獻標識號：A

Abstract： In Wireless Sensor Networks（WSNs）， how to defense DoS/DDoS attack efficiently is one of the challenging security problems. This paper combined with the current defense strategies in WSNs， establishes the model based on game theory. This model prevents malicious nodes from DoS/DDoS attack by optimizing the threshold of firewall and giving malicious nodes punishment， which lower the income of the malicious nodes. Finally， the experiments further verify the efficiency of the proposed optimized defense strategies by comparing the present defense strategies and the optimized ones， to achieve the purpose of preventing DoS/DDoS attack.

Keywords： WSNs； DoS/DDoS Attack； Game Theory； Defense Strategies Optimization

0 引言

近年來，無線傳感器網絡（Wireless Sensor Networks，簡稱WSNs）在軍事、農業、環境監測等各個領域都有廣泛的應用。這是一種全新的信息獲取、處理和傳輸技術。由于無線傳感器網絡具有組網快捷、靈活、不受有線網絡約束等特點，使得無線傳感器網絡作為現代通信技術中一個新的研究領域，引起了學術界和工業界的高度重視。但是，又因為WSNs具有通信能力有限，節點能量有限、動態的網絡拓撲等結構特點，使得WSNs容易受到攻擊，因而網絡安全引起了人們的極大關注，各種預防網絡攻擊的安全措施相繼被提出。

在眾多的網絡攻擊中，拒絕服務攻擊（Denial of Service，簡稱DoS攻擊）的危害尤為嚴重[1]。當攻擊者控制大量的節點進行DoS攻擊時，這種攻擊方式就被歸類為分布式拒絕攻擊（Distributed Denial of Service，簡稱DDoS攻擊）。攻擊者在WSNs中發起DoS/DDoS攻擊時，一般會通過持續發送重放或偽造的報文給網絡中的某些節點的方法，使這些節點不停的轉發數據包，從而導致有限的節點能量被迅速消耗殆盡，最后導致WSNs的癱瘓。

近年來，大量學者對WSNs中的DOS/DDoS攻擊的防御策略的研究問題表現出了極大的興趣，紛紛展開了該領域的研究工作 [2-6]。針對無線傳感器網絡安全問題，不少學者提出使用博弈論的方法來解決在WSNs中的DoS/DDoS防御問題，這也是研究方向之一[7-10]。文獻[11]總結了如何用不同的博弈模型研究WSNs中的安全問題。文獻[12]介紹了一種基于博弈論的DDoS入侵檢測防御策略。文獻[13]給出了在WSNs中Dos/DDoS攻擊的協議分析。本文在上述文獻的基礎上，提出了一種基于兩個參與者、非合作非零和博弈的模型，用來分析WSNs中DoS/DDoS的防御策略優化問題。現有的WSNs網絡防御技術分兩種比較普遍的方式。第一種方式就是建立防火墻，這是防御WSNs中DoS/DDoS攻擊最直接的策略，通過直接過濾速率較高的數據流來進行防御；第二種方式是采用入侵檢測系統，對檢測到的攻擊節點采取措施。本文針對WSNs的網絡拓撲的特點，結合上述兩種防御方式，使用博弈模型進行策略優化。

本文選擇的博弈模型優點在于模型的靈活性高，可以在保持具體方法不變的前提下，根據不同的WSNs網絡環境調整對應的參數，這樣的模型適用于實際應用。本文的創新點在于，利用簡單的博弈模型將上述使用的兩種防御措施相結合；另外，本文提出了一種通用的防御優化方式，在實際使用時可以根據具體的WSNs環境設置相應的參數，因此，該策略適用于不同的WSNs網絡環境。

1 背景知識

博弈論是研究存在利益沖突的參與者之間的行為和決策的理論和方法。博弈論也可以被理解為用于模擬兩個或兩個以上的決策者在一定條件下相互作用的關系[14]。具體就是通過嚴格的數學理論和模型推導，在各種策略之間進行利益權衡，從而選擇對參與者自身最有利的策略。本文將WSNs中DoS/DDoS攻擊看作是攻擊者和防御者的相互關系，攻擊者和防御者都會選擇對自己最有利的策略以實現自己的利益最大化。一般來說，決策者可以分為理性決策者和非理性決策者。理性決策者在選擇決策時會考慮他人的策略，而非理性決策者不會。在大多數的博弈模型中，決策者都是理性決策者。

在博弈過程中，每個決策者都以自己的利益最優作為選擇決策的依據，由于每個決策者做出的決策會影響其他的決策者的利益，所以納什均衡（Nash equilibrium）的概念就被提了出來。納什均衡又被稱為非合作博弈均衡，是一種策略組合，使得每個參與者的決策是對其他參與者策略的最優反應。如果一個博弈存在納什均衡，而決策者沒有選擇納什均衡中的策略的話，那么其收益一定低于選擇納什均衡中的策略帶來的收益。

博弈模型的類型可以根據博弈的參與者之間是否存在約束性的條件或者一致達成堅不可破的聯盟而被劃分為合作博弈和非合作博弈。決策者根據各自的策略集來判斷是否合作。在DoS/DDoS攻擊中，攻擊者和防御者沒有相互的合作關系，因此這個模型屬于非合作博弈。此外博弈模型又可以劃分為零和博弈與非零和博弈。當決策者的總收益之和存在變化時，這種博弈類型稱為非零和博弈。

2 基于博弈模型的防御策略優化

2.1 概述

本文基于WSNs現有的防御方式，利用博弈模型實現防御策略優化的目的。其中，博弈模型是一個基于兩個參與者的非合作一次零和博弈。為了更好地刻畫攻擊者和防御者之間的關系，該模型包括了DoS/DDoS攻擊者和防御者考慮的多個因素。在該博弈模型中，攻擊者的目標是找到最優的攻擊配置參數，以此達到花費最小，收益最大的目的；而另一方面，防御者的目的也是找到最優的防御配置參數，以此來降低攻擊者的收益。本文假定攻擊者是一個理性的攻擊者，也就是說攻擊者總是以收益最大化作為自己的目的。由于本文的模型是一個一次博弈模型，這也就意味著雙方選定策略之后，將不會改變各自相應策略直到博弈結束；而非零和博弈意味著，攻擊者與防御者的收益公式將分開計算，并且攻擊者與防御者的收益之間沒直接的聯系。當找到了博弈模型中的納什均衡點時，就表示找到了優化策略的最優解。

2.2 網絡拓撲及現有的防御措施

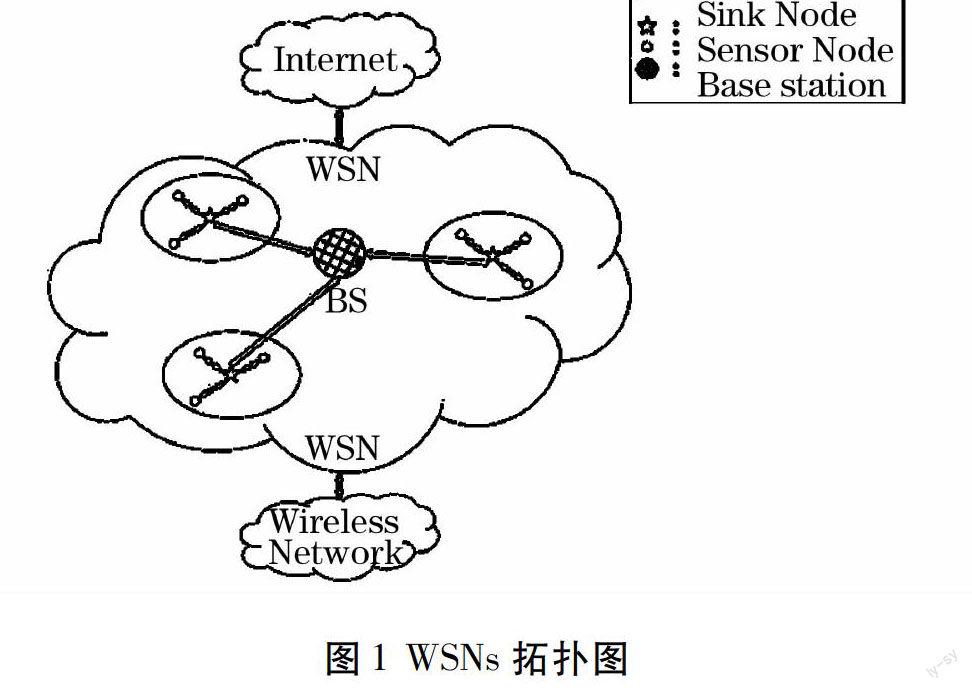
本文使用文獻[15]中的網絡拓撲。圖1中的網絡拓撲是WSNs中常見的網絡拓撲圖。圖1中間的部分就是WSNs，與其相連的可能有Internet以及其他的無線網絡。WSNs采取聚簇結構，每個簇中有一個Sink節點（Sink Node）以及一些傳感器節點（Sensor Node）。Sink節點監控每一個傳感器節點的行為，并將傳感器的信息發送給基站（Base Station），最后通過基站與其他網絡連接。由于WSNs的資源有限性，Sink節點到基站的帶寬是存在瓶頸的，而WSNs與其他網絡連接時，其帶寬可以假設不存在瓶頸。

圖2顯示了當WSNs網絡中存在正常節點以及攻擊節點時，防御措施是如何工作的。在Sink節點到基站中間中會有兩層防御設施。首先，第一層的防火墻會將數據包速率超過閾值的數據包丟棄。之后的第二層防御措施是一個入侵檢測系統，當有攻擊行為被檢測出來時，系統會發出警告。

2.3優化策略的引入

本文提出了兩種優化策略：

（1）給出優化的防火墻閥值，以達到最優的防御效果。因為現有的防火墻措施是將速率超過一定閾值的數據包丟棄，然而，這個閾值如何設定比較合理，很難做出判斷。如果閾值設定得過高將使防御效果降低，但是過低的閾值也會導致正常的節點無法使用。

（2））針對檢測出的攻擊節點給予一個優化的懲罰值。現有的入侵檢測系統缺乏懲罰措施，使得攻擊節點無須考慮攻擊行為對后續收益的影響[16]。

實際上，攻擊者的總收益取決于以下四個因素：

（1）被攻擊節點消耗的平均帶寬；（2）由于瓶頸的限制而導致正常節點數據包丟失的數量；（3）攻擊者使用的攻擊節點的數量[15]；（4）被防御措施懲罰的時間。

其中，（1）和（2）中的收益是正收益，而（3）和（4）中的收益是負收益。如果攻擊節點在攻擊之后會得到懲罰，使得攻擊的成本大于收益，那么，一個理性的攻擊者將不采取攻擊的行為，從而有效地遏制攻擊行為。

2.4優化策略的計算

本文的博弈模型中，參與者是攻擊者與防御者。攻擊者的行動分為攻擊與不攻擊兩種，記為行動集 。而對于防御者而言，由于WSNs的資源有限性以及開啟防御措施的能量消耗，防御者在實際中并不一定需要時時刻刻地開啟防御措施，因此，防御者的行動為防御與不防御，記為行動集 。最終的博弈行動集記為 。由于攻防雙方選擇策略時均無限制，所以最終的博弈策略空間為 。

攻擊者與防御者每個人選擇一個策略，那么n維向量 稱為一個策略組合，其中 是參與者i選擇的策略。用 表示參與者選擇其策略集j策略。對于特定的策略組合，參與者i的收益記為 。由于這里的博弈模型是非零和博弈，所以對于收益滿足如下公式：

2.4.1 WSNs網絡

假定在WSNs網絡中，包括正常節點 是正常節點數）和攻擊節點 是攻擊節點數）。DoS攻擊可以看作是攻擊節點數a為1的DDoS攻擊。所有的節點發送的都是基于UDP協議的數據包。在模擬UPD數據流時，通常認為UDP數據包的速率服從某一種確定的概率分布或者是多種概率分布的混合，比如正態分布、指數分布、對數分布等等。在本文的模型中，每一個合法節點以某一種速率發送數據包到基站，這種速率是服從泊松分布的，如公式（2）所示：

公式（2）中， 表示正常節點發送的數據包速率， 是正常節點發送數據包速率的數學期望。為了模擬合法的數據流的流率，攻擊節點也同樣地使自身的發包速率服從概率分布，這個概率分布 可能是泊松分布 ，或指數分布 ，或正態分布 。這里的 是攻擊節點速率的數學期望， 是攻擊節點速率的方差。之所以考慮指數分布和正態分布是為了考慮多種因素以更好地概括攻擊者的行為。

2.4.2 攻擊者收益

在計算攻擊者收益時，需要考慮2.4概述中提到博弈空間的四種策略組合，必須結合防御者選擇的策略，然后才能分別進行計算。本節將依次計算四種策略組合下的攻擊者收益。

（1）攻擊者選擇不攻擊，防御者選擇不防御時：

由于攻擊者選擇不攻擊，所以攻擊者額外的消耗帶寬，沒有導致正常節點的數據包丟失，自身沒有消耗額外的能量，也不會被防御措施懲罰。在這種情況下，攻擊者的收益為0，可以用公式（3）表示：

（2）攻擊者選擇不攻擊，防御者選擇防御時：

攻擊者的收益同情況（1）相同，如下所示：

（3） 攻擊者選擇攻擊，防御者選擇不防御時：

由于防御者選擇不防御，防火墻與入侵檢測系統將不會影響攻擊節點。所以攻擊者的收益只受三部分影響： ， 和 。定義 是被攻擊者消耗的平均帶寬， 是正常節點數據包丟失的比率， 是轉化的代價。 的計算方式如公式（6）所示：

在計算 時，由于UPD協議為了保持通訊需要發送心跳包，所以為了保持協議，數據包的速率有一個最低值，低于該速率的數據包不能傳送到目的地。定義 是可以傳送數據包的最低速率， 是瓶頸處的帶寬上限，則 如公式（6）所示：

公式中， 表示 比 小的概率。定義 ，分別是被攻擊節點消耗的平均帶寬、正常節點的丟失比率和使用的僵尸節點數的權重系數，攻擊者的收益如公式（7）所示：

（4） 攻擊者選擇攻擊，防御者選擇防御時：

在計算該部分時需要考慮防火墻與入侵檢測系統。在實際過程中，由于防火墻的存在，無論是正常節點還是攻擊者，速率高的數據包將會被防火墻攔截。這個情況導致了正常節點的平均速率發生了改變；同時，攻擊節點的平均速率也會因為防火墻的攔截發生改變。假定防火墻攔截數據包的速率閾值為 ，公式（8）和（9）表示了新的速率是如何計算的：

再考慮入侵檢測系統，假設攻擊者的某一個攻擊節點在持續攻擊了 時間之后，以概率 被檢測出是攻擊節點，那么在被檢測出是攻擊節點的基礎上，入侵檢測系統將會持續 段時間丟棄該節點的數據包，而這個主動丟棄的措施對于攻擊者來說是透明的，攻擊者在 段時間的攻擊就相當于沒有任何收益的。假設攻擊節點在攻擊 時間之后恒定地以 的概率被檢測出來，被懲罰 段時間，那么攻擊者在這段時間的收益可以用兩部分來表示，如公式（12）所示：

上述公式中， 是數據包的速率， 是縮放因子， 是影響參數，是瓶頸處的帶寬上限。圖3給出了不同值的情況下，檢測率 的變化趨勢。從圖中可以分析得出，不一樣的影響參數將會得到不一樣的檢測率曲線。對于速率較低的數據包，檢測率將比較高；而對于速率較高的數據包，檢測率將會降低，但是由于防火墻的存在，所以速率較高的數據包有很大的可能性在第一層防御的時候就被攔截。

2.4.3 防御者收益

影響防御者的收益的主要因素有如下幾點：

（1）正常用戶消耗的平均帶寬；（2）防御措施成功防御的攻擊；（3）防御措施自生消耗的能量；（4）防御措施將正常用戶攔截的數量。上述的這四點中，第一點與第二點均是啟用防御措施帶給防御者的正收益，而第三點與第四點則是負收益。

同攻擊者的收益計算方式相同的是，計算防御者收益時同樣必須按照策略的組合分四種情況進行分析討論。

（1） 攻擊者選擇不攻擊，防御者選擇不防御時：

在這種情況下，由于攻擊者沒有采取任何攻擊行為，所以防御者的收益只有正常用戶消耗的平均帶寬帶來的收益。定義 是正常節點消耗帶寬的權重系數，防御者的收益如公式（17）所示：

（2） 攻擊者選擇不攻擊，防御者選擇防御時：

定義 是啟用防御措施而帶來的消耗的權重系數，是由于防御措施而導致受影響的正常節點數的權重系數，則這種情況下防御者的收益如公式（18）所示：

（3） 攻擊者選擇攻擊，防御者選擇不防御時：

在這種情況下，由于防御者沒有采取任何的防御措施，將不會有攻擊者被攔截。但是相對地，也沒有產生任何因防御措施帶來的消耗。由于瓶頸處的帶寬上限，將會有部分的正常節點被丟棄，這也會對防御者的收益產生影響。防御者的收益公式如下：

（4） 攻擊者選擇攻擊，防御者選擇防御時：

由于攻擊者的攻擊，使得正常節點消耗的平均帶寬下降。啟用防御措施會帶來消耗，但是啟用了防御措施后，將使攻擊的數量下降，防火墻將攔截速率高的攻擊節點，入侵檢測系統通過檢測將給予懲罰。另外，啟用防御措施帶來不利的一面就是會影響正常節點的工作。定義是成功防御攻擊節點的權重系數，則防御者具體的收益公式如下：

2.4.4 納什均衡計算

本文中，非零和博弈的收益矩陣如表4所示。

在表1的基礎上，結合2.4.2與2.4.3中收益的計算公式，并根據攻擊者選擇的決策進行討論。

由于該博弈是一個純策略博弈，那么在這種模型下，只需找到攻擊者與防御者的納什均衡，即能選擇防御者的策略。通過計算可以發現，在防御者選擇防御時，攻擊者選擇攻擊的收益大于不攻擊的收益，在防御者選擇不防御時，攻擊者同樣是選擇攻擊的收益較高，所以攻擊者一定會選擇進行攻擊；防御者的計算方式也是相同的，所以博弈中策略組合（攻擊，防御）是一個納什均衡。

由于該博弈是非合作博弈，所以防御者的目的是使自身的收益提高，對方的收益下降，也就是使雙方的收益變大。定義攻擊者的參數集是 ，防御者的參數集是（ ）。公式（21）是防御者參數集的計算方式。

綜上所述，防御者只需在特定的WSNs環境中，找到滿足公式（21）的參數組合，就是防御者最終得到的優化策略。

3實驗分析

為了更好地解釋實際情況中納什均衡的計算，本節將對WSNs中的參數進行設置，并使用工具模擬在假定環境下的納什均衡解。

假設正常節點數 ，節點發送的數據包速率服從泊松分布并且平均速率 ；Sink節點到基站的數據通訊瓶頸限制是5Mbps；使協議保持通訊至少需要的速率是 設定如下的限制： （僅限正態分布）。

首先討論在攻擊者選擇攻擊，防御者選擇防御的情況下，攻擊者的收益情況。由于最后的收益公式相對較為復雜，本文采取從簡到繁的方法，一步一步討論。圖4表示的是攻擊者的收益，攻擊者發送的數據流服從泊松分布，。在這個例子中，攻擊者能調整的參數只有僵尸節點的數量，防御者能調整的參數只有閥值。可以看到，當值低的時候，攻擊者的收益很高，這是因為過低的值提高了丟棄正常節點的數據包的概率。另一方面，當防御者提高其閾值時，攻擊者的收益降低了，這個是符合理論的事實，因為閾值提高，較少的正常的節點被防火墻攔截。同時觀察到，當攻擊者增加其僵尸節點數量時，所收益降低，這也是符合事實的一點。納什均衡的點是攻擊者使用89個僵尸節點，防火墻的值在128時。這時的收益是。

圖4是博弈中的一個子博弈，在圖4的基礎上，進一步地模擬攻擊者的模型。在第2節中已提到，攻擊者發送的數據包的速率不是單一地服從泊松分布的，速率可以服從泊松分布，正態分布或者是指數分布，那么將這些情況都考慮進來，構成包含多種分布的子博弈。具體的計算過程如算法1所示。

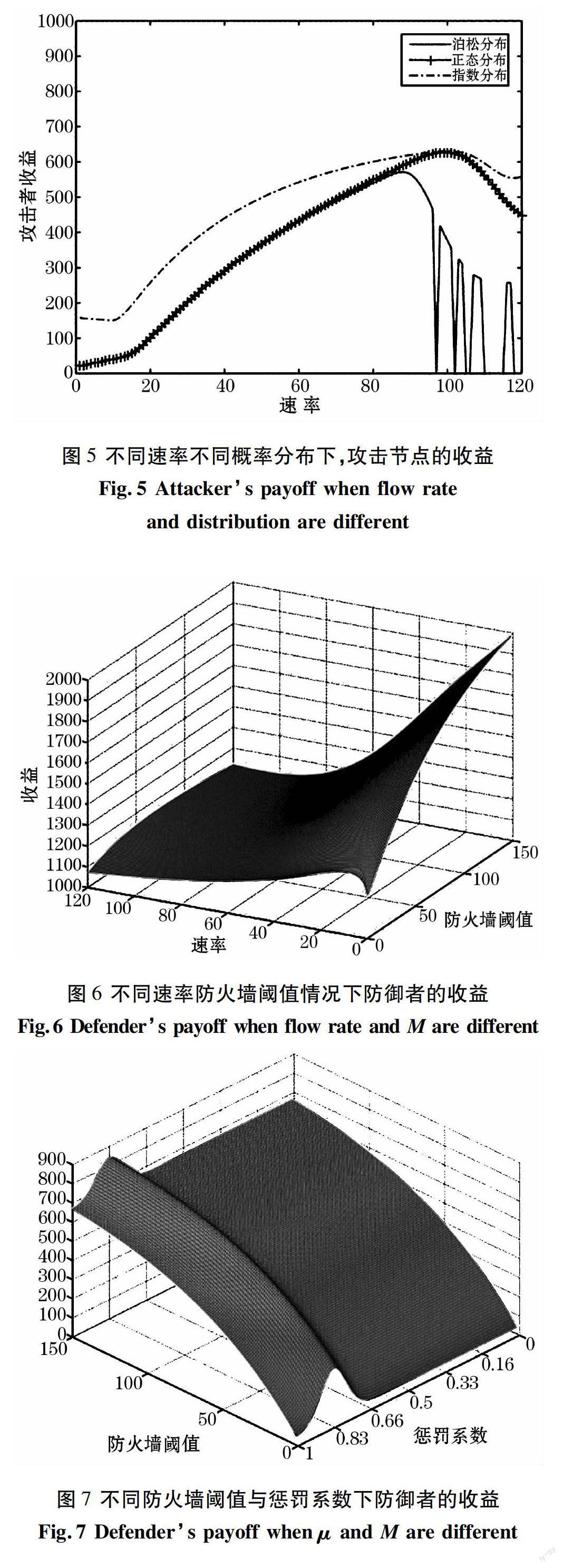
如圖5所示，具體顯示了不同概率分布，不同速率下的納什均衡點。在攻擊者選擇泊松分布的情況下，攻擊者的最高收益出現在速率為88Kbps時，最高收益是504；在攻擊者選擇正態分布的情況下，攻擊者的最高收益出現在速率為99Kbps時，最高收益是604；在攻擊者選擇指數分布的情況下，攻擊者的最高收益出現在速率為100Kbps時，最高收益是630。從圖5中可以發現，選擇指數分布在該WSNs環境中幾乎都是優于其他分布的。

再計算防御方的收益，防御者在考慮攻擊者不同速率的情況下，防御者的自身最高收益如圖6所示。

從圖6可以看出，在攻擊者速率較低的時候，防御者的收益較大，同時，隨著防火墻閥值的上升，防御者的收益不斷上升；而當攻擊者速率上升的時候，防御者的收益有所下降，這是由于攻擊者占用的帶寬不斷上升的原因，并且此時，隨著防火墻閾值的上升，防御者的收益不再是一直上升，而是到達某一個值之后就開始出現下滑，說明隨著閾值的上升，防御的效果變得不再明顯。假設當攻擊者發送的數據包速率為100時，防火墻設到70時將使防御者收益最高。

而最后真正決定防火墻閥值 與懲罰系數 應該取何值，還是需要計算防御者與攻擊者收益的差值，圖7顯示了不同防火墻閥值與不同懲罰系數 的情況下，收益的差值情況。

從圖中可以看出，在懲罰系數選擇為0.83，并且防火墻閾值選擇在150時，防御者與攻擊者的收益差值最大。表2顯示了攻防雙方最高收益下的參數配置：

綜上所述，在實驗給定的WSNs環境下，防御者將防火墻的閥值設定在150Kbps，懲罰系數 的條件下，會使攻擊者收益降到最低。與現有的防御策略相比較，首先，現有的防火墻閾值如果沒有設定在最優值，攻方雙方的收益差可能得到更高的收益，而將閾值設定在最優值上，無論攻擊者如何更改攻擊參數，在理論上攻防雙發的收益差降到最低；其次，現有的入侵檢測系統的警告作用并不能降低攻擊者的收益，而引入懲罰機制會使攻擊者的收益進一步的降低。實驗表明，提出的兩個防御優化策略能使防御效果更加有效。

另外，本實驗是在確定的參數下進行分析，通過模擬分析防御策略優化的有效性。通過其他實驗發現，在本文的博弈模型基礎上，利用參數調節來設置不同的WSNs環境，提出的防御優化策略同樣有效。

4 結束語

本文針對WSNs中DoS/DDoS攻擊防御的過程，利用博弈論的方法進行建模。在現有的防御措施防火墻以及入侵檢測系統的基礎上，分別提出了如何合理有效地設置防火墻閾值，以及在入侵檢測系統中引入懲罰措施的優化策略，使得攻擊節點的收益降低，從而達到有效防御的效果。本文提出的優化策略可以適用于不同WSNs環境，為WSNs中DoS/DDoS攻擊防御策略優化提供了理論的基礎。

參考文獻：

[1] FOUCHAL S， MANSOURI D， MOKDAD L， et al. Recursive-clustering-based approach for denial of service （DoS） attacks in wireless sensors networks[J]. International Journal of Communication Systems. 2015， 28（2）： 309-324.

[2] RAJA K N， BENO M M. On securing Wireless Sensor Network-Novel authentication scheme against DOS attacks[J]. Journal of Medical Systems. 2014， 38（10）：84-85.

[3] LEE S M， KIM D S， LEE J H. Detection of DDoS attacks using optimized traffic matrix[J]. Computers and Mathematics with Applications， 2012， 63（2）： 501-510.

[4] 李晉，曹曉梅. WSN中抗DoS攻擊的廣播認證方案[J]. 計算機應用. 2014， （S1）： 43-46.

[5] WANG H， JIA Q， DEN F. A moving target DDoS defense mechanism[J]. Computer Communications， 2014， 46（15）： 10-21.

[6] SON Y H， HONG J K， BAE K S. Authentication masking code against DoS of T-MAC protocol[J]. Journal of Central South University， 2013， 20（7）： 1889-1895.

[7] LIANG X， XIAO Y. Game theory for network security[J]. IEEE Communications Surveys and Tutorials， 2013， 15（1）： 472-486.

[8] FALLAH M. A puzzle-based defence strategy against flooding attacks using game theory[J]. IEEE Transactions on Dependable and Secure Computing， 2010， 7：5-19.

[9] AMIRTHAVALLI K， SIVAKUMAR P. Comparison of AODV， Dos attack and Game theory in power conservation in wireless sensor networks[J]. IEEE Transactions on Communications and Mobile Computing， 2009， 3：507-511.

[10] WU Q， SHIVA S， ROY S， et al. On modeling and simulation of game theory-based defence mechanisms against DoS and DDoS attacks[J]. Society for Computer Simulation， 2010 （159）：1-8.

[11] SHEN S， YUE G， CAO Q， et al. A survey of game theory in wireless sensor networks security[J]. Journal of Networks， 2011， 6（ 3） ： 521-532.

[12] MOOSAVI H， BUI F M. A game-theoretic framework for robust optimal intrusion detection in wireless sensor networks[J]. IEEE Transactions on Information Forensics and Security， 2014， 9（9）： 1367-1379.

[13] MIHAJLOV B， BOGDANOSKI M. Analysis of the WSN MAC protocols under jamming DoS attack[J]. International Journal of Network Security， 2014， 16（4）： 304-312.

[14] 李慧芳，姜勝明，韋崗. 無線傳感器網絡中基于博弈論的路由建模[J]. 傳感技術學報. 2007， 20（9）： 1-3.

[15] SHAHABODDIN S， AHMED P， LAIHA M， et al. Cooperative game theoretic approach using fuzzy Q-learning for detecting and preventing intrusions in wireless sensor networks[J]. Engineering Applications of Artificial Intelligence， 2014（32）： 228-241.

[16] 楊黎斌，慕德俊，蔡曉妍. 基于博弈理論的傳感器網絡拒絕服務攻擊限制模型[J]. 傳感技術學報. 2009， （01）： 90-94.

[17] SPYRIDOPOULOS T， KARANIKAS G， TRYFONAS T. A game theoretic defence framework against DoS/DDoS cyber attacks[J]. Computers and Security， 2013， 38： 39-50.