悄然升溫的函數新貴
——取整函數

☉湖北省武漢市第一中學 張友成

悄然升溫的函數新貴
——取整函數

☉湖北省武漢市第一中學 張友成

近年來，一些省市調考、聯考以及高考數學試卷中，取整函數先是低調出場，接著悄然升溫.就命題形式而言，選擇題形式的考題有之，填空題形式的考題有之，解答題形式的考題也有之；就試題難易程度而言，容易題有之，中等題有之，難題也有之.下面略舉幾例.

例1 （湖北省八校2013屆高三第二次聯考理科數學第9題）已知x∈R，符號［x］表示不超過x的最大整數，若函數f（x）=-a有且僅有3個零點，則a的取值范圍是（ ）.

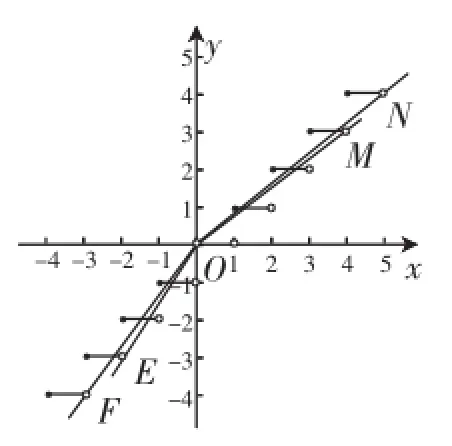
圖1

點評：解決此題的關鍵有二，一是將較為復雜的函數f（x）=-a的零點問題轉化為較為簡單的函數y=ax與函數y=［x］的圖像交點問題，二是正確作出函數y=［x］（x≠0）的圖像，這個圖像呈階梯形狀，圖像簡單，線條明快.在這里，既考查了轉化與化歸的基本數學思想，又考查了分段作圖的基本數學方法，特別是所作圖像除一條“線段”兩端均無“端點”外，其余“線段”均是有“左端點”而無“右端點”，這就考查得比較細膩了.此題對函數圖像要求較高，筆者所在學校2013屆高三學生也參加了此次聯考，考試后機器閱卷，電腦數據顯示，此題得分情況很不理想，比第10題的得分率還要低，是選擇題中得分率最低的考題.此題是選擇題倒數第2題，系副壓軸題，當屬難題.

例2 （陜西省2013年高考理科數學第10題）設［x］表示不大于x的最大整數，則對任意實數x、y，有（ ）.

A.［-x］=-［x］ B.［2x］=2［x］

C.［x+y］≤［x］+［y］ D.［x-y］≤［x］-［y］

解析：對于選項A，取x=-1.1，則［-x］=［1.1］=1，而-［x］=-［-1.1］=-（-2）=2，故選項A不正確；對于選項B，令x=1.5，則［2x］=3，而2［x］=2，故選項B不正確；對于選項C，令x=-1.5，y=-2.5，則［x+y］=-4，但［x］=-2，［y］=-3，有［x］+［y］=-5，故選項C不正確；從而選項D正確.

點評：也可正面證明選項D正確.令x=［x］+α，y=［y］+ β，其中，0≤α＜1，0≤β＜1，則x-y=［x］-［y］+α-β，其中-1＜α-β＜1.若0≤α-β＜1，則［x-y］=［x］-［y］；若-1＜α-β＜0，則0＜1+α-β＜1，推出：x-y=［x］-［y］+α-β=［x］-［y］-1+（1+αβ）?［x-y］=［x］-［y］-1＜［x］-［y］.故總有［x-y］≤［x］-［y］.此題是選擇題的壓軸題，其絕對難度并不是很大，但高中課本新教材（人教A版）從頭到尾一直沒有涉及取整函數y=［x］，學生面對的是一個新概念、新背景、新領域，故相對難度還是很大的.這樣命題，既有新意又不失偏頗.這樣的試題，堪稱“好題”.這一年，陜西省文科數學中也有一道關于取整函數y=［x］的試題，也是“好題”.

例3 （湖北省2013年高考文科數學第8題）設x為實數，［x］為不超過x的最大整數，則函數f（x）=x-［x］在R上為（ ）.

A.奇函數 B.偶函數 C.增函數 D.周期函數

解析：令x=1.1，則f（1.1）=1.1-［1.1］=0.1，但f（-1.1）= -1.1-［-1.1］=-1.1+2=0.9，故選項A、B均錯.

由f（1.9）=0.9，f（2.1）=0.1，得選項C也錯.

從而選項D正確.

點評：當n∈Z，n≤x＜n+1時，f（x）=x-［x］=x-n，故可分段作出f（x）=x-［x］的圖像（如圖2），這樣就能直接選出正確答案D.

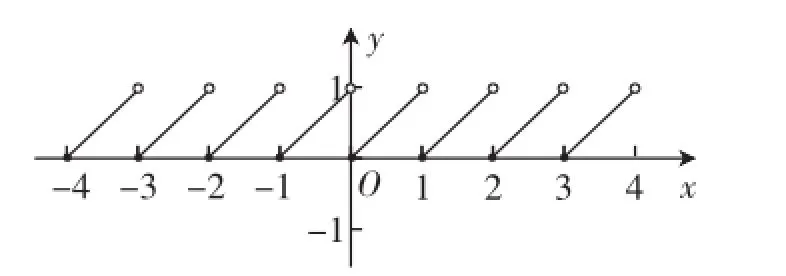
圖2

需要關注的是，對于任意一個正數x，［x］表示其整數部分，x-［x］表示其小數部分，通常用符號｛x｝表示，它有許多簡潔而有趣的性質，例如：對任意x∈R，函數y=｛x｝的值域為［0，1）；若n∈N，x∈R，則｛n+x｝=｛x｝，此等式表明y=｛x｝是一個以1為周期的周期函數等.可以說，函數y=｛x｝與函數y=［x］相伴相隨，相映成趣.

取整函數也稱高斯函數INT（x），它有多種類型，如四舍五入取整函數Round（x），上取整函數y=［x］，下取整函數y=［x］，若不特別說明，取整函數y=［x］通常指下取整函數.取整函數y=［x］，以往不時出現在各級各類競賽或自主招生考試中，頗受命題組的青睞，但在高考中還鮮有出現，現在，既然取整函數y=［x］不約而同地出現在一些省市的高考試卷上了，并且還有悄然升溫的征兆，那么研究一下取整函數的一些基本性質就有一定的意義了，下面給出取整函數y=［x］的幾條性質.

性質1：對任意x∈R，均有x-1＜［x］≤x＜［x］+1；

性質2：取整函數是一個不減函數，即對任意實數x1、x2，若x1≤x2，則［x1］≤［x2］；

性質3：若n∈N，x∈R，則［n+x］=n+［x］；

性質4：若x∈R，y∈R，則［x］+［y］≤［x+y］≤［x］+［y］+1；

性質5：若n∈N+，x∈R，則［nx］≥n［x］；

最后，應該指出，取整函數與微積分有著緊密聯系，它在科學和工程上有廣泛應用.可以展望，隨著高考命題研究的不斷深入，取整函數［x］的“出鏡率”將越來越高，這是一個方興未艾的研究課題，是一塊尚待深入發掘的熱土.A