問題表述多元性 等價轉(zhuǎn)化變直觀
——解答函數(shù)問題中的轉(zhuǎn)化思想

☉江蘇省宿遷中學(xué) 徐紅兵

問題表述多元性 等價轉(zhuǎn)化變直觀
——解答函數(shù)問題中的轉(zhuǎn)化思想

☉江蘇省宿遷中學(xué) 徐紅兵

“化歸與轉(zhuǎn)化思想”是高中數(shù)學(xué)幾大常規(guī)數(shù)學(xué)思想之一，數(shù)學(xué)解題的過程也可以稱之為轉(zhuǎn)化的過程，即將復(fù)雜問題簡單化、抽象問題直觀化、未知轉(zhuǎn)化為已知、一般問題化為特殊問題等，本文以近幾年高考中的函數(shù)問題為例，就解題中所涉及的轉(zhuǎn)化思想分析說明，供同學(xué)們復(fù)習(xí)參考.

一、巧借對稱——化被動為主動

對稱性是函數(shù)的重要性質(zhì)之一，主要包括函數(shù)圖像關(guān)于x軸或y軸對稱、關(guān)于某條直線對稱、關(guān)于原點對稱、關(guān)于某一點成中心對稱，其中既包括函數(shù)自身的對稱性，也包括兩函數(shù)之間的對稱性.

例1 （2014年高考湖南卷）已知函數(shù)f（x）=x2+ex-（x＜0）與g（x）=x2+ln（x+a）的圖像上存在關(guān)于y軸對稱的點，則a的取值范圍是（ ）.

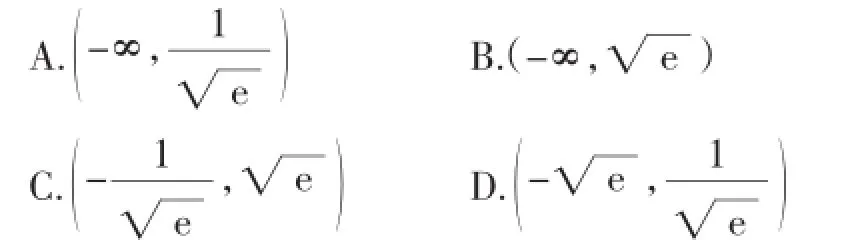
解析：已知函數(shù)f（x）=x2+ex-（x＜0）與g（x）=x2+ ln（x+a）的圖像上存在關(guān)于y軸對稱的點，則問題可等價轉(zhuǎn)化為函數(shù)f（x）=x2+ex-（x＜0）關(guān)于y軸對稱的函數(shù)f（-x）=（-x）2+e-x-與g（x）=x2+ ln（x+a）的圖像有交點，即（-x）2+e-x-=x2+ln（x+a）有解，化簡得e-x-=ln（x+a），結(jié)合圖像（如圖1）.

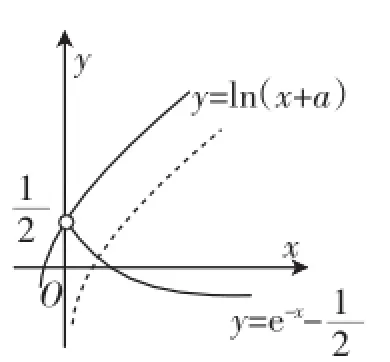
圖1

評注：本題解答中，將兩函數(shù)存在關(guān)于y軸對稱的點，對稱轉(zhuǎn)化為兩個函數(shù)的交點問題，進而將問題求解.在利用函數(shù)的對稱性求解相關(guān)問題時，要注意變量的變與不變.

二、等價換元——化陌生為熟悉

化陌生為熟悉，是等價轉(zhuǎn)化思想的精髓所在，高中數(shù)學(xué)解題的過程，其實就是化生為熟的過程，即將陌生的問題化為我們熟悉的問題解答.

例2 （2014年高考全國）若函數(shù)f（x）=cos2x+asinx在區(qū)間上是減函數(shù)，則a的取值范圍是_________.

解析：f（x）=cos2x+asinx=-2sin2x+asinx+1，令sinx=t，則f（x）=-2t2+at+1.因為x∈），所以t∈所以f（x）=-2t2+at+1，t∈因為f（x）=cos2x+asinx在區(qū)間上是減函數(shù)，所以f（x）=-2t2+at+1在區(qū)間上是減函數(shù).又對稱軸為x=，所以，即a∈（-∞，2］.

評注：本題解答中，經(jīng)過換元將陌生的函數(shù)化為我們熟悉的二次函數(shù)，進而利用二次函數(shù)最值問題求解.

三、參數(shù)分離——化煩瑣為簡潔

參數(shù)分離，即將參數(shù)從已知所給的函數(shù)關(guān)系中分離出來，使問題轉(zhuǎn)化為確定的函數(shù)與常數(shù)函數(shù)（參數(shù)為常數(shù)）之間的關(guān)系，進而將問題簡潔求解.

例3 （2014年高考天津）已知函數(shù)f（x）=|x2+3x|，x∈R.若方程f（x）-a|x-1|=0恰有4個互異的實數(shù)根，則實數(shù)a的取值范圍為_________.

圖2

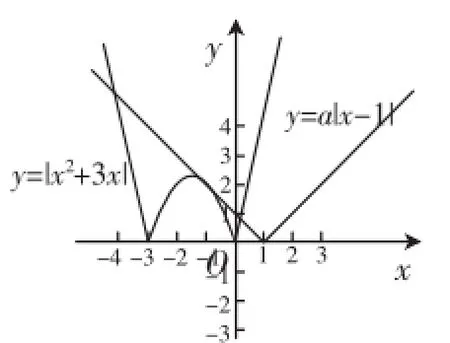
圖3

評注：本題也可在同一坐標系內(nèi)分別作出y=f（x）與y= a|x-1|的圖像，如圖3所示.當y= a|x-1|與y=f（x）的圖像相切時，由整理得x2+（3-a）x+a=0，則Δ=（3-a）2-4a=a2-10a+9=0，解得a=1或a= 9.故當y=a|x-1|與y=f（x）的圖像有4個交點時，0＜a＜1或a＞9.

四、分類討論——化不定為確定

在眾多函數(shù)問題中，大部分都帶有參數(shù)，因參數(shù)的取值范圍不同，造成函數(shù)的解析式、圖像、性質(zhì)不同，因此在解題中對參數(shù)的分類討論必不可少.

例4 （2014年高考湖北）已知函數(shù)f（x）是定義在R上的奇函數(shù)，當x≥0時，f（x）=（|x-a2|+|x-2a2|-3a2）.若?x∈R，f（x-1）≤f（x），則實數(shù)a的取值范圍為（ ）.

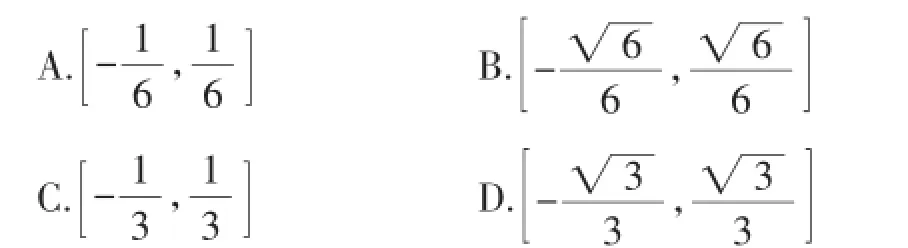
因此，根據(jù)奇函數(shù)的圖像關(guān)于原點對稱作出函數(shù)f（x）在R上的大致圖像，如圖4.

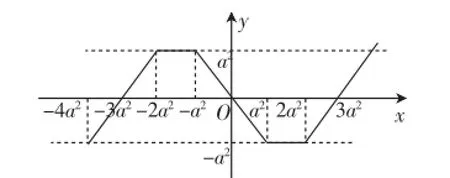
圖4

觀察圖像可知，要使?x∈R，f（x-1）≤f（x），則需滿足2a2-（-4a2）≤1，解得-.故選B.

評注：分類討論的運用，可將復(fù)雜的問題分解為幾個基本的簡單問題，進而各個擊破.應(yīng)用分類討論的過程中，要注意分類標準的選擇不重復(fù)、不遺漏.本題以x的取值為分類標準，將不確定的函數(shù)關(guān)系式轉(zhuǎn)化為確定的函數(shù)關(guān)系式，使問題得以順利解決.

五、借助具體函數(shù)——化一般為特殊

近幾年來全國及各省市的高考題都或多或少地出現(xiàn)了一些我們從未見過的新題型，面對這些挑戰(zhàn)時，有些學(xué)生不知所措，其實“新”并不等于“難”，題型“新”不等于解法“新”.

例5 （2013年高考福建）設(shè)S、T是R上的兩個非空子集，如果存在一個從S到T的函數(shù)y=f（x）滿足：

（1）T=｛f（x）|x∈S｝；

（2）對任意x1、x2∈S，當x1＜x2時，恒有f（x1）＜f（x2），那么稱這兩個集合“保序同構(gòu)”.

以下集合對不是“保序同構(gòu)”的是（ ）.

A.A=N*，B=N

B.A=｛x|-1≤x≤3｝，B=｛x|x=-8或0＜x≤10｝

C.A=｛x|0＜x＜1｝，B=R

D.A=Z，B=Q

解析：對于選項A，取f（x）=x-1，x∈N*，滿足條件，所以A=N*，B=N是“保序同構(gòu)”，應(yīng)排除A.

故選D.

評注：從陌生的情景中尋找已學(xué)過的函數(shù)知識背景，設(shè)法建立溝通已知與未知的聯(lián)系，尋求轉(zhuǎn)化的途徑是本題求解的關(guān)鍵.解答中所運用的排除法是解決選擇題的一個重要方法，根據(jù)所給的條件，構(gòu)造出符合條件的函數(shù)，進而利用特殊函數(shù)的性質(zhì)得出結(jié)論.F