基于位置和速度觀測的空間穩定系統快速對準

何虔恩，吳秋平

基于位置和速度觀測的空間穩定系統快速對準

何虔恩，吳秋平

（清華大學 精密儀器系，北京 100084）

空間穩定系統是高精度長航時導航技術的關鍵，快速對準是其工程應用的重要功能之一。研究了基于位置和速度觀測的系統快速對準方法。基于Wahba定姿原理設計平臺姿態角的粗估計算法，研究了系統水平通道誤差模型的短時可觀測性，并據此設計一個可實時估計平臺失準角初值、水平位置和速度誤差的7維精對準Kalman濾波器。計算機仿真和動態試驗結果表明，所述快速對準方法可估計較大的平臺失準角（3°量級），同時適用于系泊和海上應急啟動情況；在動態條件下精對準2 h，精度即滿足指標要求，具有較強的工程應用價值。

空間穩定系統；快速對準；位置和速度觀測；Kalman濾波

空間穩定平臺式慣性導航系統（簡稱空間穩定系統）是一種航位推算系統，其精度依賴于初始條件設定精度。例如，為達到0.1 n mile/h的導航精度，初始方位和水平失準角應分別小于30"和6"，并且初始速度誤差應小于0.1 kn。因此，為取得高精度導航性能，系統必須具有高精度的初始條件設定[1]。其中，初始速度和位置通過全球衛星定位系統等外部設備容易獲得，所以系統初始化的主要任務在于“對準”，即減小方位和水平失準角。

一般情況下，系統在運載體停泊狀態下進行正常啟動，有足夠長（至少1天）的時間進行對準并標定慣性儀表參數。但在實際應用中不可避免地會遇到執行突發緊急任務的情況，此時要求系統能夠快速啟動并具備規定的導航精度。另外，空間穩定系統是一復雜的光機電系統，零部件在長期工作過程和環境中各種沖擊、振動的作用下不可避免地會出現一些故障，在故障修復后，仍然面臨快速啟動的問題。

慣性導航系統（簡稱慣導）有自對準法、傳遞對準法和光學對準法等對準方法[1]。其中，自對準法便捷、可操作性強，且同時適用于靜基座和動基座，在實踐中取得廣泛應用。對于地球上的導航，慣導系統的自對準本質上是一個構建三維空間正交系作為要對準到的參考坐標系的過程，這里主要利用的是相互不平行的本地重力矢量和地球自轉角速度矢量。目前，自對準法主要有兩類實現方案：I）基于比力矢量一次積分觀測和Wahba定姿原理的方案[2-3]。該方案概念形象直觀，且適用于估計任意大小的初始失準角，但對各種隨機干擾（如：發動機振動、風浪擾動等）比較敏感，因而對準精度較低。文獻[3]給出其準靜態條件下方位對準的仿真精度為4.8'（1σ）/120 s；文獻[2]給出其搖擺條件下方位對準和水平對準的試驗精度分別為3'/1000 s和14"/1000 s。這一方案主要用于低精度捷聯慣導的自對準或高精度慣導的粗對準場合。II）基于導航誤差（位置誤差、速度誤差和姿態誤差）觀測的方案[4-5]。根據對準誤差傳遞到導航誤差的特性，設計線性/非線性濾波器估計對準誤差并予以校正來達到對準的目的。該方案抵抗各種隨機干擾的能力比第一類方案強，對準精度高——在動態條件下方位和水平對準的仿真精度可分別達到4.2'/300 s和20"/300 s（基于姿態誤差觀測）[5]，因而常用于高精度慣導的精對準場合。不足的是，該方案要求初始失準角為小角度，一般需要借助于傳遞對準（有外參考基準時）或粗對準來滿足這一條件。

對于上述第二類自對準方案，選擇不同的觀測量，對準的性能（精度和快速性）是不同的：按快速性排列，由快到慢依次是基于姿態誤差、速度誤差和位置誤差觀測，然而相應的對準精度卻是依次提高的。對于捷聯式慣導系統而言，快速性要求較高（對準時間通常不超過20 min），一般采用基于姿態誤差/速度誤差的自對準方案，這是公開發表的文獻所集中討論的。但對于空間穩定系統，即使在快速啟動的情況下，對精度的要求也是較高的（對準精度應達到角秒量級），此時宜采用基于位置誤差/速度誤差的自對準方案，這正是本文研究的出發點。借鑒捷聯式慣導系統自對準方法的研究經驗，本文探討適用于空間穩定系統的快速對準方案。

1 快速對準總體方案

快速對準分兩步：I）粗對準，將平臺坐標系（P系）對準到指定的參考坐標系（地球坐標系，e系），并粗略估計P系相對e系的姿態角；II）精對準，精確化第一步中的P系姿態角粗略估計值。

1.1 粗對準

① 在碼頭系泊條件下，利用方位參考基準和三軸加速度計輸出的比力信息將P系對準到e系。

② 在海上動態條件下，利用另一套同類慣導輸出的框架角或外部姿態參考基準將P系對準到e系。

③ 采用基于Wahba定姿原理的自對準方案粗略估計P系的姿態角，這一步主要考慮到初始失準角可能較大的情況（如海上動態環境下）。若能保證初始失準角較小（如在系泊和靜止基座條件下），利用單點比力數據估計P系姿態角即可[1]。

實現以上第①和②兩項內容已有比較成熟的技術和成功的經驗，不再贅述。第③項內容的實現算法將在第2節討論。

1.2 精對準

如圖1所示，引入水平位置和速度的外參考信息，與慣導解算得到的相應信息作差，作為精對準濾波器的觀測量。精對準濾波器運行一段時間達到平穩后，作出平臺失準角的估計，并以之修正慣導解算回路中的P系姿態角。

圖1 精對準方案框圖Fig.1 Diagram of the fine alignment

2 P系姿態角粗估計

2.1 P系姿態角及導航解算動力學方程

P系姿態角定義為由e系依次繞-x、y和-z軸旋轉到P系的三個Euler角，分別記為S1、σ1和γ2，則P系到e系的坐標轉換陣可表示為

式中，cij表示的第i行第j列元素，i,j=1,2,3。

導航解算動力學方程可表示為[1]

式中：re——在e系中表示的系統位置矢量；

ve——在e系中表示的系統地速矢量；

fP——在P系中表示的比力矢量；

ge——在e系中表示的本地重力加速度矢量；

ωie——地球自轉角速率；

ωx, ωy, ωz——P系運動角速度在P系中的投影。

2.2 粗估計算法

借鑒文獻[2]中的捷聯慣導對準方法，記初始時刻分別與e系和P系重合的慣性坐標系為e0系和P0系，則可分解為

xyzPxφy和φz的微分方程與方程(3)相似：

且初值φx(0)=φy(0)=φz(0)=0。給定P系運動角速度，由方程(5)可數值求解φx、φy和φz，進而可得0PPC。

將式(4)代入(3)的第二個微分方程，整理后可得

式中：

等式(6)兩邊同時右乘αT(t)，并對時間進行一次積分，則等式(6)給出P系初始姿態矩陣的最小二乘解：

文獻[2]已經證明，只要在[0, t]區間上的所有α（τ）能夠支起三維空間，則α（τ）αT（τ）dτ可逆，因而式(8)成立。對于地球上的低速載體導航，上述條件是容易滿足的，因為在慣性系中觀看，本地重力矢量形成的軌跡是一圓錐面，而重力又是比力α（τ）的主導分量，所以，α（τ）的軌跡也近乎一圓錐面，因而能支起三維空間。

將式(8)代入式(4)，再根據式(2)，即可估計出P系姿態角。由式(7)可知，α(t)和β(t)計算易受各種隨機運動和加速度計固有噪聲的干擾，加之積分時間有限，矩陣α（）αT（）dτ條件數較大。因此，通過上ττ述方法估計P系姿態角的精度往往較低，對于高精度慣導，還需要精對準對這一估計結果進行精化。

3 精對準

3.1 系統誤差模型

引入高度阻尼后，慣導垂直通道的誤差可忽略不計，此時，對于低速巡航載體，水平通道的誤差方程可寫為[1]

式中：δrN, δrE——位置誤差的北向和東向分量；

δvN, δvE——速度誤差的北向和東向分量；

ωD=-ωiesinL ，L為本地地理緯度；

s

ω——Schuler振蕩角頻率，1.24×10-3rad/s；

g——本地重力加速度值；

▽N, ▽E——比力誤差的北向和東向分量；

ψN, ψE——平臺失準角的北向和東向分量，滿足如下關系式：

式中，λ——相對地理經度，初始時刻為0。

對式(3)中的平臺運動微分方程取擾動，略去平臺漂移誤差及二階誤差量（經驗表明，平臺常值漂移重復性誤差約1×10-4(°)/h，對快速（≤2 h）對準的影響小于1"），經推導，可得平臺失準角的解析表達式為[1]3.2 平臺失準角的可觀測性

選擇經緯度誤差和水平速度誤差為觀測變量，并記觀測向量為z=[δLδλcosLδvNδvE]T，則

式中，ra——地球平均半徑。對于低速運載體，在精對準期間經緯度變化為小量。簡單起見，考慮S1和σ1為小量的情況，此時式(10)可簡化為

將式(11)代入式(13)，再與式(12)一同代入方程(9)，整理后可得

易見，常值項、sinωiet和cosωiet是相互正交的，當t足夠大（大于1天）時，可分離ΔS1（0）、Δσ1（0）、?N/g和Δγ2（0）+?E/(gcosL)。然而，為滿足快速性要求，t通常較小，此時式(14)可簡化為

顯然，等號左邊均為關于t的一次多項式，各項可分解為兩部分：I）誤差源（平臺失準角初值和比力誤差北/東向分量或其線性組合）；II）放大系數。按照放大系數從大到小順序排列各項，如表1所示。誤差源的放大系數反映單位該誤差量對觀測值的貢獻，在相同噪聲環境下，放大系數越大，相應誤差源越容易在觀測值中反映出來（或者說它的可觀測性越強），因而在相同時間內的估計精度越高。

表1 誤差源及其放大系數Tab.1 Error sources and their amplifying coefficients

由表1可知，在短時間內，Δσ1（0）+?N/g 可觀測性最強，而欲達到同等可觀測性（以放大系數大小表征），對于ΔS1（0）和Δγ2（0）+?E/(gcosL)（后者的估計依賴于前者），額外需要3.8 h；對于Δσ1（0），額外需要更長時間。

在低（高）緯度地區，Δσ1（0）(Δγ2（0）+?E/(gcosL))幾乎是不可觀測的，因此，為快速精確估計全部平臺失準角，要求：I）在中低緯度地區進行對準；II）濾波器至少運行到ΔS1（0）收斂為止；III）比力誤差的北向和東向分量盡可能小（經過標校，加速度計誤差引起的比力誤差可忽略不計，而重力垂線偏差引起的比力誤差需視具體動態環境作相應的補償）。

另外，從式(12)可知，事實上僅需觀測水平位置誤差或速度誤差即可分離三個失準角，同時觀測這兩種誤差主要是為了增加觀測數據，以便在同樣的對準時間內取得更高的濾波精度。

3.3 精對準Kalman濾波器設計

基于第3.2節討論，選擇增廣狀態向量為

將式(11)代入式(10)，再代入方程(9)可得4個時變狀態量的動態方程；3個平臺失準角初值為定常狀態量，因此，可得如下增廣狀態方程：

式中：F(t)——7×7維系統矩陣，各元素根據(9)～(11)是明顯的；

w(t)——7×1維狀態噪聲向量。

另外，根據第3.2節的討論，觀測方程為

式中：H——4×7維觀測矩陣，

n(t)——4×1維觀測噪聲向量。令狀態噪聲w(t)和觀測噪聲n(t)為相互獨立的零均值Gauss白噪聲，且協方差陣滿足

這里，δ(t)——Dirac函數。又令初始狀態為x0，相應的協方差陣為P0，則根據狀態方程(15)和觀測方程(16)，容易設計7維精對準Kalman濾波器，對x進行實時估計。Kalman濾波器的具體公式可參閱文獻[1]。

4 計算機仿真

假設系統所處位置的緯度為40°，高度為0 m；陀螺常值漂移為1×10-3(°)/h量級，加速度計附加幅值為1×10-3m/s2的零均值白噪聲；采樣周期為10 Hz；平臺姿態角初值分別為S1(0)=3°、σ1(0)=0.2334°和γ2(0)=0°。根據上述快速對準算法和空間穩定系統的機械編排，依次進行粗對準、精對準和導航解算（陀螺漂移系數置為常規初始對準與標定結果）。圖2摘錄了某三組仿真實驗對準期間的平臺失準角曲線。

圖2 對準期間的平臺失準角曲線（仿真）Fig.2 Platform misalignment angles during alignments (simulation)

由圖2易見：I）持續粗對準（A組曲線）對應的ΔS1和Δσ1需100 min才能收斂到3.3ρ以內（ρ表示指標要求），而Δγ2僅需30 min；II）粗對準進行12 min后（此時，平臺失準角收斂到1200ρ以內）就開始精對準（B組曲線），平臺失準角收斂速度慢，甚至發散；III）若粗對準進行47 min后（此時，平臺失準角收斂到60ρ以內）再開始精對準（C組曲線），精對準分別進行11 min和56 min即可使.Δσ1和ΔS1（或Δγ2）收斂到ρ以內，這主要是由于初始失準角較小時，精對準濾波器所采用系統模型的線性化誤差小，濾波精度較高，同時這也印證了保證精對準濾波器精度控制平臺初始失準角小到一定范圍內的必要性。

依次進行47 min粗對準和56 min精對準后開始導航解算，所得經緯度誤差曲線如圖3所示。易見，經度誤差主要包含-ρ的偏置和幅值約ρ、周期約24 h的余弦分量；緯度誤差包含同周期同幅值的正弦分量，根據空間穩定系統誤差傳播特性分析結果[1]知，這主要由初始失準角ΔS1(t0)和Δγ2(t0)引起，表明S1和γ2的對準誤差約為ρ，而σ1的對準誤差不顯著。另外，經緯度誤差中還包含趨勢項和（或）發散振蕩分量，這主要由陀螺常值漂移系數誤差引起。

圖3 導航經緯度誤差（仿真）Fig.3 Longitude and latitude errors (simulation)

5 試驗結果

某套空間穩定系統在緯度為9°～23°的區域進行了系泊狀態和海上動態試驗。利用在線記錄的系統試驗數據和外參考數據（如：計程儀速度和GPS經緯度），對前述快速對準算法進行離線驗證（陀螺漂移系數置為常規初始對準與標定結果）。與計算機仿真情況不同，這里平臺姿態角真值未知，因此，以平臺失準角初值（平臺姿態角初值的實時估計值減去相應穩態值）的收斂情況來衡量對準的性能。

下面摘錄利用某兩段數據進行算法驗證的情況。兩段數據分別來自系泊和海上環境，載體速度分別為0～0.07 m/s和0.2～0.6 m/s，加速度計隨機噪聲的幅值分別為0.005～0.015 m/s2和0.4～1 m/s2。

5.1 對準結果

持續進行粗對準24 h，可得系泊狀態和海上動態條件下的粗對準曲線，其變化規律與圖2的A組曲線相似。表2給出相應平臺失準角初值分別收斂到1200ρ、600ρ、200ρ、60ρ和20ρ所需要的時間。

表2 粗對準過程平臺失準角初值收斂特性Tab.2 Convergence features of initial platform misalignment angles during coarse alignment

由表2易見，在同等環境下，隨著指定收斂范圍縮小，所需粗對準時間急劇上升，尤其是對準到20ρ所需時間是對準到60ρ.的3倍以上。另外，收斂到相同范圍，海上環境所需粗對準時間是系泊狀態的1.6～2倍，其主要原因是在海上由風浪、洋流等引起的載體運動干擾和加速度計隨機噪聲比系泊狀態大2倍以上，結合式(7)和(8)分析知，這將降低粗對準性能。

令粗對準進行47 min后（由表2知，此時平臺失準角不超過600ρ）開始精對準并持續4 h，可得系泊狀態和海上動態條件下的精對準曲線，其變化規律與圖2的C組曲線相似。表3給出相應平臺失準角初值分別收斂到20ρ、10ρ、6.6ρ、3.3ρ和ρ所需時間。

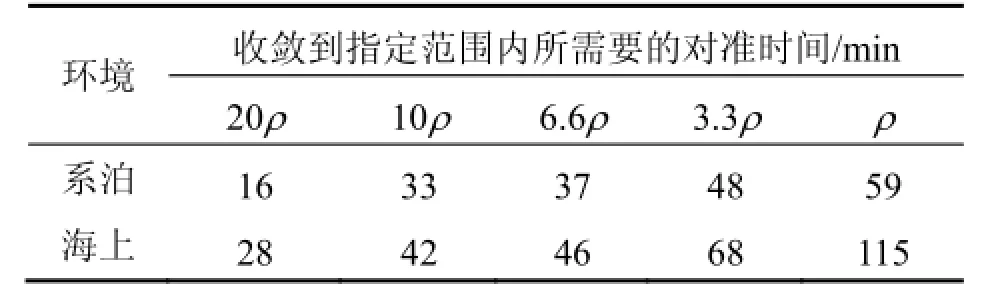
表3 精對準過程平臺失準角初值收斂特性Tab.3 Convergence features of initial platform misalignment angles during fine alignment

由表3可見，收斂范圍從20ρ.縮小到ρ，精對準所需時間的差異不超過一個量級；收斂到相同范圍，海上環境所需精對準時間是系泊狀態的1.2～2倍。將表2和表3對照可以看出，花費同等量級的時間，精對準精度比粗對準高一個數量級以上。

5.2 導航結果

令粗對準進行47 min，精對準在系泊和海上環境下分別進行1 h和2 h，然后進行導航解算，圖4摘錄了相應的導航經緯度誤差歸一化曲線。易見，經緯度誤差中主要包含由隨機干擾引起的Schuler周期振蕩分量，且海上對應的分量比系泊大一倍以上；而周期為24 h的正余弦分量的幅值以及偏置均小于ρ，該結果表明，前述對準過程的精度優于ρ。另外，在導航初始階段，海上環境對應的經緯誤差出現顯著的Schuler周期的超調振蕩，這主要由速度初值誤差引起，因為在精對準過程所用的速度參考信息來自電磁計程儀，此時，計程儀零偏和洋流等將不可避免地造成參考速度的偏置誤差（可達0.3 m/s），從而導致速度的初值誤差，而這對平臺失準角初值估計的影響是可忽略不計的（根據文獻[1]知，0.1 m/s的參考速度偏置誤差引起的對準誤差小于0.4"）。

圖4 歸一化導航經緯度誤差（試驗）Fig.4 Normalized longitude and latitude errors (experiments)

6 結論與展望

針對長航時高精度空間穩定系統的快速啟動需求，研究了基于位置和速度觀測的系統快速對準方法。基于Wahba定姿原理開發了一種可粗略估計較大平臺失準角的粗對準算法。研究了系統水平通道誤差模型的短時可觀測性，并設計了一個可實時估計平臺初始失準角、水平速度和位置誤差的7維精對準Kalman濾波器。進行了計算機仿真和動態試驗研究，結果表明，所述快速對準方法有效、實用，特別是在動態條件下精對準2 h精度即達到ρ，滿足系統快速啟動需求。

在快速啟動時，平臺常值漂移誤差可達1×10-4(°)/h，如前所述，這對快速對準的影響可忽略不計，但對系統長時間導航精度的影響是難以容忍的，可利用精對準過程中位置和速度觀測的殘差序列對之進行建模，并在導航階段預以實時補償。這里，較為實用的是偏置分離濾波器[6]（偏置強可觀）和考慮濾波器理論[7-8]（偏置弱可觀），這些將在后續研究中進一步討論。

（References）：

[1] 高鐘毓. 慣性導航系統技術[M]. 北京: 清華大學出版社, 2012: 184-389.

[2] Wu M P, Wu Y X, Hu X P, et al. Optimization-based alignment for inertial navigation systems: Theory and algorithm[J]. Aerospace Science and Technology, 2011: 1-17.

[3] Peter M G. Coarse alignment of a ship’s strapdown inertial attitude reference system using velocity loci[J]. IEEE Transactions on Instrumentation and Measurement, 2011, 60(6): 1930-1941.

[4] Ali J, Mirza M R U. Initial orientation of inertial navigation system realized through nonlinear modeling and filtering[J]. Measurement, 2011, 44(5): 793-801.

[5] Cao S Y, Guo L. Multi-objective robust initial alignment algorithm for inertial navigation system with multiple disturbances[J]. Aerospace Science and Technology, 2012, 21(1): 1-6.

[6] Friedland B. Treatment of bias in recursive filtering[J]. IEEE Transactions on Automatic Control, 1969, 14(4): 359-367.

[7] Zanetti R, Bishop R H. Kalman filters with uncompensated biases[J]. Journal of Guidance, Control, and Dynamics, 2012, 35(1): 327-330.

[8] 何虔恩, 高鐘毓, 吳秋平. 基于未補償偏置濾波器的慣導動態初始對準[J]. 中國慣性技術學報, 2015, 23(2): 184-188.

He Q E, Gao Z Y, Wu Q P. Initial alignment based on uncompensated bias filter for inertial navigation systems under dynamic conditions[J]. Journal of Chinese Inertial Technology, 2015, 23(2): 184-188.

Fast alignment of space-stable systems based on position and velocity observations

HE Qian-en, WU Qiu-ping
(Department of Precision Instruments, Tsinghua University, Beijing 100084, China)

Space-stable systems are the key to high-precision long-term navigation technology, in which fast alignment is one of the most important functions in engineering applications. In this paper, a system fast alignment method based on position and velocity observations is investigated, and a coarse alignment algorithm based on Wahba’s attitude determination principle is developed. The short-time observability of system horizontal error model is analyzed, then a seven-dimension Kalman filter is designed to estimate the real-time initial platform non-alignment angles, horizontal position and velocity errors. Simulations results and dynamic experiments show that the presented fast alignment approach is efficient in estimating large platform non-alignment angles (a magnitude of 3°) and can be adopted in urgent starting situations whether in port or on the sea. The expected dynamic accuracy can be achieved in two hours for fine alignment, which is of great value in engineering applications.

space-stable systems; fast alignment; position and velocity observations; Kalman filtering

U666.1

A

2015-02-10；

2015-06-04

總裝“十二五”預研項目（51309030401）

何虔恩（1985—），男，博士后，研究方向為導航系統與控制。E-mail：heqianen2005@126.com

聯 系 人：吳秋平（1972—），男，副研究員，博士生導師。E-mail：wuqiuping@mail.tsinghua.edu.cn