力的動態平衡分析法

陳天瑜

動態平衡即某一過程中物體處于一系列的平衡狀態下，物體所受合力雖恒為零，但組成合力的“成員”作用在發生變化. 分析這類問題，可采用控制變量的思想，先定量研究某參量確定下的一個平衡態，得到各“成員”的變化規律，再討論該參量變化時各“成員”的變化情況.

平行四邊形定則是力、運動、加速度等所有矢量的合成與分解都遵循的矢量運算的最基本定則.

例1 如圖1所示，把球夾在豎直墻AC和木板BC之間，不計摩擦. 設球對墻的壓力為FN1，球對板的壓力為FN2，則在將板BC逐漸放至水平的過程中（ ）

A. FN1和FN2都增大

B. FN1和FN2都減小

C. FN1增大，FN2減小

D. FN1減小，FN2增大

解析 雖然題目中的FN1和FN2涉及的是墻和木板的受力情況，但研究對象還是只能取球. 在將板[BC]逐漸放至水平的過程中，球時刻處于動態平衡狀態，FN1和FN2都是變力，可以先畫開始時刻的受力圖，然后再根據力的關系討論力的變化規律.

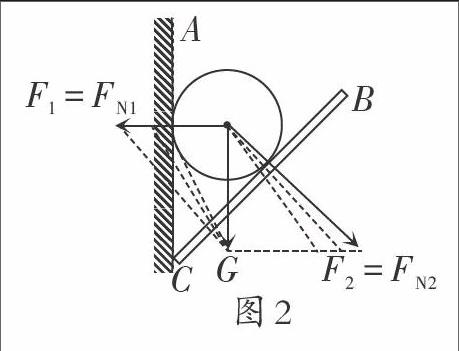
方法一：分解法. 球所受的重力[G]產生的效果有兩個，一是球對墻的壓力FN1，二是球對板的壓力FN2. 根據這兩個效果將其分解，則F1=FN1，F2=FN2，如圖2所示，從動態變化圖中不難看出，在板[BC]逐漸放平的過程中，FN1的方向保持不變而大小逐漸減小，FN2與[G]的夾角逐漸變小，其大小也逐漸減小.

方法二：合成法. 由于球處于平衡狀態，彈力FN1、FN2的合力F跟重力是一對平衡力，其大小、方向均不變，如圖3甲所示，畫出力的矢量三角形如圖3乙所示，在板[BC]逐漸放平的過程中，除合力F恒定外，墻對球的彈力FN1的方向也不改變，而FN2繞[O]點為軸……