基于UKF區域交叉定位的WSNs Sink節點動態跟蹤算法*

姚依翔， 謝俊元

(1.南京大學 計算機科學與技術系, 江蘇 南京 210093; 2.計算機軟件新技術國家重點實驗室,江蘇 南京 210093; 3.南京曉莊學院 數學與信息技術學院,江蘇 南京211100)

基于UKF區域交叉定位的WSNs Sink節點動態跟蹤算法*

姚依翔1,3， 謝俊元1,2

(1.南京大學 計算機科學與技術系, 江蘇 南京 210093; 2.計算機軟件新技術國家重點實驗室,江蘇 南京 210093; 3.南京曉莊學院 數學與信息技術學院,江蘇 南京211100)

為了提高無線傳感器網絡(WSNs)使用壽命，對WSNs的目標跟蹤方式進行研究，提出基于無跡Kalman濾波(UKF)的WSNs Sink節點動態跟蹤算法,以實現高效節能的資源管理和利用方式。首先利用UKF算法對目標節點的下一位置進行預測，然后通過四圓區域定位交叉定位算法對Sink節點的位置區域進行局部準確定位。實驗結果表明:這種動態的Sink節點預測定位算法能夠有效縮短數據發射傳感器和Sink點之間的距離,減少跳數，從而實現負載均衡降低能耗的效果。

無線傳感器網絡； 無跡卡爾曼濾波； 區域交叉定位； Sink節點； 動態跟蹤

0 引 言

目前國內外學者在無線傳感器網絡(WSNs)的算法層面、網絡層面和物理層面做了大量研究[1～3]。對于動態Sink節點WSNs和Sink節點的跟蹤算法的研究有很多文獻提出可行方案。文獻[4]為防止過多的節點被激活從而浪費能量資源，提出一種基于邊界檢測的Sink節點跟蹤算法，但是當對象的速度和方向突然發生變化時會影響邊界檢測的準確性；文獻[5]提出傳感器對周圍環境進行監測并定期向服務器傳送數據，由服務器采用三角測量的方法完成對目標位置的定位，但是這種方法過分依賴于目標發出信號的強度，當噪聲或者障礙物存在時會造成信號的衰減，進而造成目標定位的失準；文獻[6]提出了一種基于二叉樹結構目標跟蹤方法，樹中的每個節點對應于WSNs中移動的傳感器目標，并在運動過程中可以動態地更新節點，根據收集到的傳感器信息可以獲得關于目標完整和準確的信息，但是當目標運動過快時效果不佳，同時樹節點頻繁地更新操作反而會增加傳感器的能量消耗。

針對上述算法的性能有待提高的問題，本文提出一種基于無跡卡爾曼濾波和區域交叉定位的動態傳感器網絡Sink節點跟蹤算法(dynamic sensor network sink node tracking algorithm based on UKF and regional cross localition，URDST)，該算法對于目標的運動不做限制，并且通過對移動節點的預測定位方式可以更好地管理傳感器的能量使用狀態，利用UKF算法預測目標可能出現的區域，對該區域內的傳感器節點進行激活，然后利用四圓定位算法對目標進行定位，通過這種方式平衡了網絡中的能量,從而降低了能源消耗量。

1 動態Sink節點的UKF預測算法

1.1 Sink節點最優位置

假設該算法在實際應用中是不依賴于網絡的狀態和目標的運動形態，Sink節點是無能量約束可以以有限的速度在區域中移動，并且在Sink層面節點的位置是已知的，相關文獻已經證明這種假設不會增加任何特定的限制條件。文獻[7]給出了一種用來計算Sink節點最優位置的目標函數，該目標函數已成功應用于靜態的Sink節點選取，但當Sink節點移動過快時，由于計算數據信息在大范圍區域中是通過隨機方式產生的，從而隨機的冗余的數據信息會導致Sink節點的移動定位存在延遲，出現定位不準確和較高的丟包率等問題。針對上述問題本文引入一個能量中心計算公式，通過快速移動目標周圍傳感器剩余能量狀況對下一時刻Sink節點的最優位置區域進行提前預測

(1)

式中 Xj(t)和Yj(t)為計算出的新的Sink節點的位置坐標，i為預測區域PRj(t)中所有的活躍節點的標識符，xi(t)和yi(t)為活躍節點為的坐標，Eneri(t)為活躍節點i的剩余能量。上式可以看出新Sink節點的位置重心與活躍節點區域的剩余能量呈反比關系，即新Sink節點將逐漸靠近低剩余能量區域附近。

1.2UKF預測算法

對于非線性的濾波問題，常用的方法有EKF和UKF方法，這種處理方式在對高階項處理時采取忽略或近似的方式，會導致誤差的增加，造成預測值與真實值偏離較多[8]。為此，相關學者提出了幾種解決方案，UKF算法便是其中一種，UKF采取UT變換方式確定算法的樣本點，并且未對傳遞系統采取近似簡化，可以較高精度地保持傳遞后的狀態量分布，由于無須求解雅可比矩陣可以處理不可導非線性問題。對于離散非線性系統，其狀態和量測方程為

(2)

式中k為時間指標，xk狀態向量，zk為量測向量，wk,vk為獨立的白噪聲。UT變換需要通過統計x的特性設計2n+1個σ點，設為ζi(i=0,1,…,2n)，σ點計算公式為

(3)

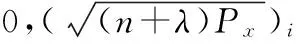
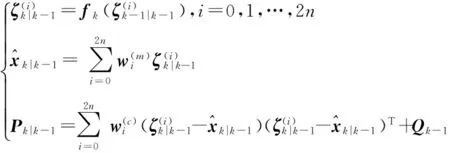
(4)

量測預測公式為

(5)

狀態的更新公式為

(6)

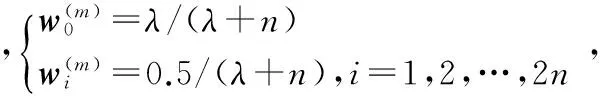
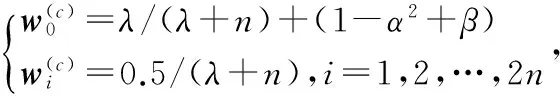
2 目標預測定位算法

2.1 預測周期

在UKF目標預測算法中，目標的移動速度是影響探測效率的關鍵因素，如果一個低速的目標進入探測區域，就可以使用該目標的前一個位置來預測他將來的位置。通過這兩個位置，可以定義一個半徑為R的圓形預測區域PR，該預測區域PR內的所有節點都是處于激活狀態。此時將Sink節點移向預測區域PR可以有效地降低活躍傳感器的傳輸能量，如果Sink節點前一時刻的位置就處于PR區域內，為了減少不必要的操作，采用下列判別式對Sink節點的移動進行限制

(L(sinkcurr,pospred)>2Range)∧

(min(Eng(i)/i∈Sd)<Δ),

(7)

式中Sd為所有參與傳輸探測傳感器數據的節點；S1為預測區域PR內所有傳感器節點的集合；Range為傳感器節點的探測范圍；Eng(i)為節點i的剩余能量；Δ為能量閾值。

如果目標的速度大幅增加，將導致傳感器不能有效地進行跟蹤，Sink節點沒有足夠的時間移動到最佳位置。所以，這里提出一種解決方案，根據公式(1)來激活探測區域，并將Sink節點提前移動到該區域，需要注意的是這種Sink節點的遷移是根據目標的速度而周期進行的。

2.2 定位算法

Sink點可以準確知道每個傳感器的具體位置，通過激活區域的傳感器探測到的目標相關信息，采用相關算法可以得到目標的具體位置。當探測區域內的傳感器密度很大時，每個目標附近的傳感器都能夠探測到目標的相關信息，如果不加區分的使用這些傳感器傳送的目標信息進行計算無疑會增加算法的計算復雜度，為了有效地解決這個問題，首先假設每個傳感器探測范圍的半徑是相等的，那么，在計算目標所在區域時沒有必要使用所有的傳感器信息而是采用本文的方法，采用四圓定位的方法可以有效地確定出目標可能出現的區域,如圖1。

假Z是包含有目標的最小區域；D是所有探測到目標的節點集合；ci,cj和ck分別是以Ni,Nj和Nk為圓心的半徑相同的圓，那么，目標的定位算法如下：

1)?Ni,Nj∈D，T1，T2為圓形區域ci和cj邊界的交點滿足，{T1,T2{=(ci)∩(cj)，由T1,T2計算穿過這兩點的直線d1。

2)在所有的節點Nk∈D-{Ni,Nj}中，尋找所有經過直線d1上[T1,T2]區域內的圓形檢測區域ck。

3)如果只有一個節點的圓形探測區域經過直線d1上[T1,T2]區域，那么，Z=(cs)∩((ci)∩(cj))，算法結束；如果有兩個節點的圓形區域cl,cm穿過直線d1上[T1,T2]區域，則計算這兩個圓形區域邊界的交點：{R1,R2}=(ci)∩(cm)，并計算經過{R1,R2}兩點的直線d2。

4)在所有的節點Nk∈D-{Ni,Nj,Nl,Nm}中，尋找所有經過直線d2上[R1,R2]區域內的圓形檢測區域。

5)如果有兩個不同的圓形區域經過直線d2上[R1,R2]區域,則計算區域Z1=((ci)∩(cm)∩Z，算法結束；如果只有一個圓cr經過上述區域，則Z=cr∩((ci)∩(cj)),算法結束。

該算法主要目的是計算出包含有目標的最小的區域，首先任意選取兩個探測到目標信息的節點來計算出兩個圓形探測區域邊界的交線。然后通過迭代的方法尋找到與交線上與[T1,T2]相交的圓形探測區域。經過上述兩步，可以尋找到滿足條件的節點，并且可以計算出經過{R1,R2}兩點的直線d2。然后采用同樣的方法計算出經過直線d2上區域[R1,R2]的圓形探測區域。最后可以得到目標所在的區域是ci,cj，ck的交叉區域，如圖1所示。“+”代表的是目標位置。

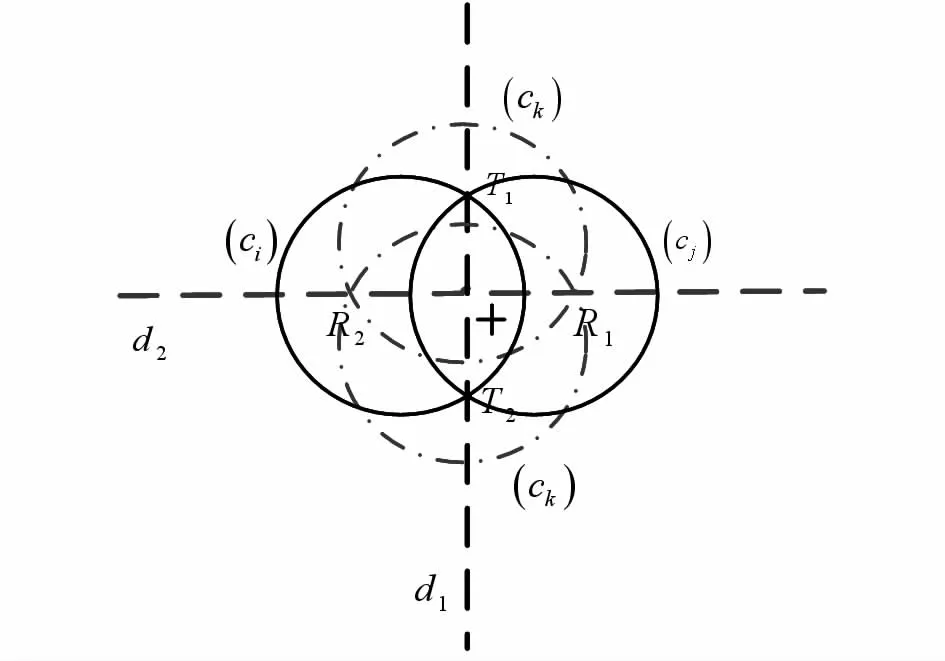
圖1 探測定位算法

3 實驗與結果分析

圖2、圖3給出的是URDST，QVF-R和QPF三種算法在目標跟蹤精度和均方誤差上的對比結果。從圖2(a)可以看出:URDST與QVF-R算法在目標跟蹤效果上相差不大，都取得了很好的效果，但是總體上URDST算法在與原有軌跡的重合度上要好于QVF-R算法，尤其是當目標軌跡突然發生變化時，URDST算法仍然能夠很好地對目標進行有效跟蹤。圖2(b)比較了URDST與QVF-R算法在跟蹤軌跡和原始軌跡之間的均方差，可以直觀的看出：URDST算法具有更小并且穩定的均方差值曲線，這說明URDST算法在跟蹤性能上更加穩定和精確。

圖3給出的是URDST和QPF的跟蹤軌跡曲線和均方差曲線，圖3(a)的軌跡曲線可以看出:QPF算法的跟蹤效果很差，甚至比QVF-R還要差，軌跡偏離原始軌跡較多，圖3(b)的均方差曲線則更準確更直觀地給出了兩種算法的精度差別，QPF均方差曲線更大并且更不穩定，這說明URDST的目標跟蹤效果要明顯優于QPF的目標跟蹤曲線。

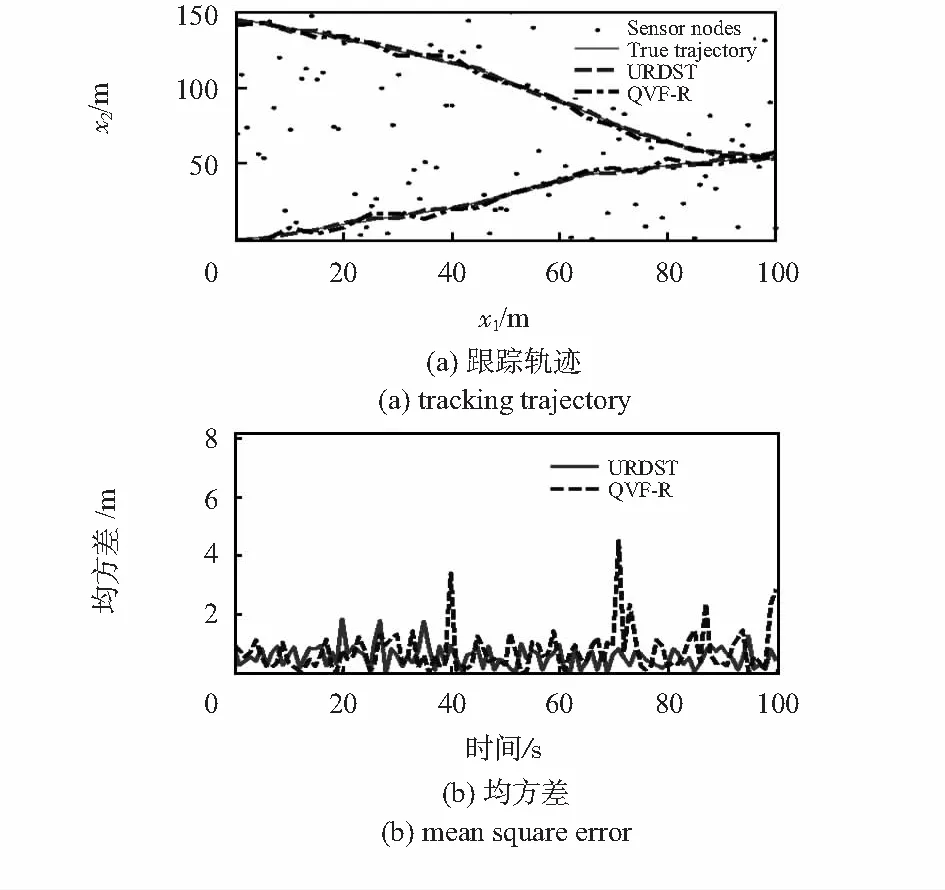
圖2 URDST與QVF-R跟蹤精度對比

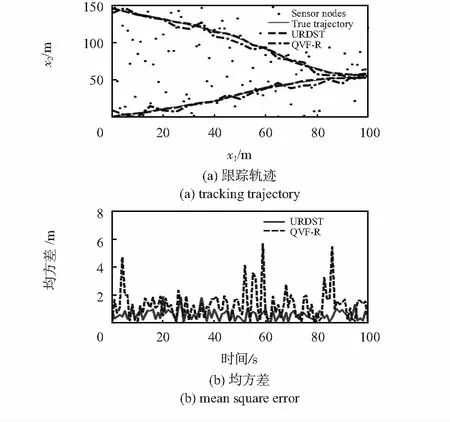
圖3 URDST與QPF跟蹤精度對比

為了對比試驗三種算法在能量消耗上的不同表現，本文采用文獻[8]提出的能量消耗評價模型，假設：1)活躍傳感器之間的數據通信時通過單跳實現的；2)同數據通信所消耗的能量相比，能量的分配和計算過程所消耗的能量可以忽略不計。數據通信所消耗的能量主要包括三部分：數據發射耗能、數據無線傳播耗能和數據接收耗能。

URDST,QVF-R和QPF三種算法在不同采樣時刻的能量消耗值對比曲線如圖4所示。

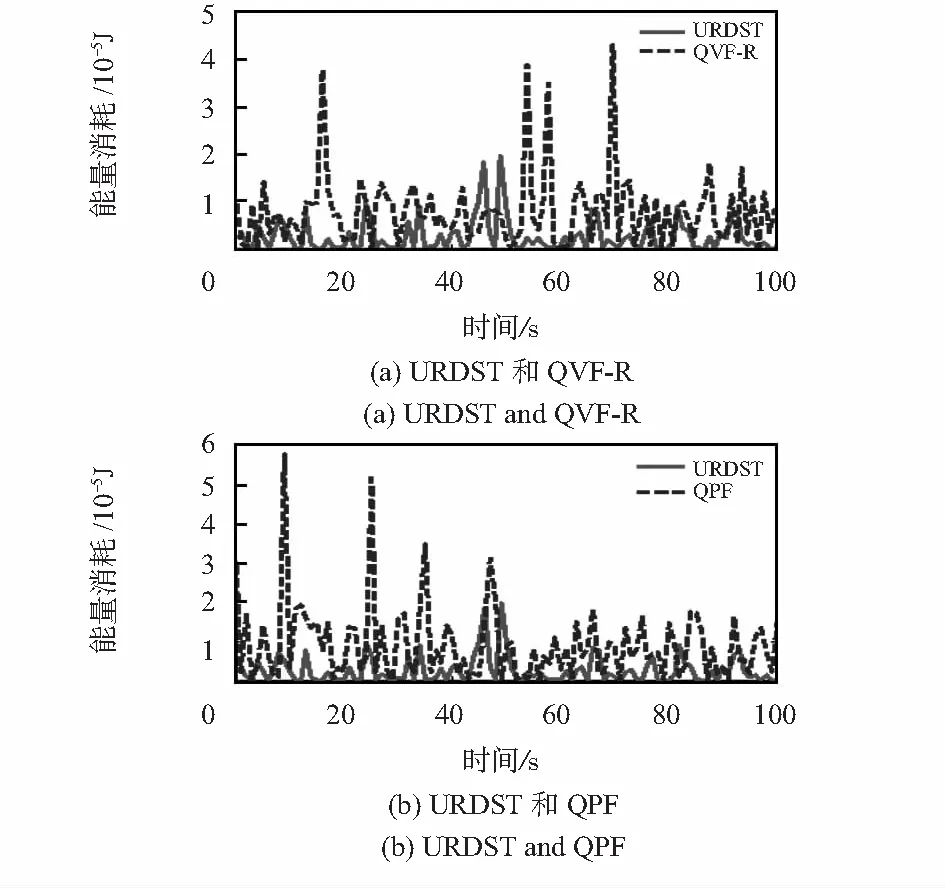
圖4 三種算法能耗對比曲線

從圖4(a)URDST和QVF-R能耗對比曲線圖中可以看出雖然在個別時刻QVF-R能耗要優于URDST算法，但是總體上看URDST算法能耗明顯要優于QVF-R算法的能耗。從圖4(b)URDST和QPF能耗對比曲線可以看出雖然在個別時刻QPF算法能耗和URDST算法能耗比較接近，但是其余時刻QPF算法能耗要明顯差于URDST算法能耗。從中可以得到以下結論：URDST相對于對比算法能夠更有效地節約能量消耗提高跟蹤精度，算法的整體性能要明顯優于QVF-R算法和QPF算法，這個結果直接證實了URDST算法在實驗室條件下的有效性與可行性。

4 結束語

本文提出了一種新的傳感器網絡目標跟蹤定位算法，主要的算法思想是通過目標的跟蹤和Sink節點的重新定位來降低網絡的平均傳輸能耗，從而有效延長WSNs的生存周期。算法包含預測和跟蹤兩個步驟,分別采用UKF一步預測算法和四圓定位算法實現了目標的準確跟蹤和定位。通過與已有的兩種跟蹤定位算法對比實驗表明：該算法的跟蹤精度和能耗節約均優于對比算法，驗證了該算法的有效性。

[1] Read J,Achutegui K.A distributed particle filter for nonlinear tracking in wireless sensor networks[J].Signal Processing,2014,98(5):121-134.

[2] Sivaranjani S,Radhakrishnan S,Thangaraj C.Adaptive delay and energy aware data aggregation technique in wireless sensor networks[J].Mobile Communication and Power Engineering,2013,296(5):41-49.

[3] Jacob J M,John A.Improving lifetime of structured deployed wireless sensor networks using sleepy algorithm[J].Eco-friendly Computing and Communication Systems,2012,305(3):47-53.

[4] Li Q L,Zhao Z J,Xu X F,et al.A flexible boundary sensing mo-del for group target tracking in wireless sensor networks[J].Green Communications and Networking,2012,51(5):25-36.

[5] Zoghi M R,Kahaei M H.Sensor management under tracking accuracy and energy constraints in wireless sensor networks[J].Ara-bian Journal for Science and Engineering,2012,37(3):721-734.

[6] Mansouri M,Ilham O,Snoussi H.Adaptive quantized target tra-cking in wireless sensor networks[J].Wireless Networks,2011,17(7):1625-1639.

[7] 吳三斌，柳 強，李成博.基于能量均衡的無線傳感器網絡路由算法[J].計算機應用研究,2012,29(4):1465-1469.

[8] 莫尚豐，陳丁潔，陳 紅.無線傳感器網絡中Top-K連接查詢處理[J].計算機學報,2013,36(3):557-570.

[9] Akkaya K,Younis M.Sink repositioning for enhanced perfor-mance in wireless sensor networks[J].Computer Networks,2005,49(4):512-534.

[10] Redondi A,Chirico M,Borsani L.An integrated system based on wireless sensor networks for patient monitoring, localization and tracking[J].Ad Hoc Networks,2013,11(1):39-53.

[11] Xu E Y,Ding Z,Dasgupta S.Target tracking and mobile sensor navigation in wireless sensor networks[J].IEEE Transactions on Mobile Computing,2013,12(1):177-186.

[12] 萬國峰，鐘 俊.基于三角形理論的無線傳感器網絡定位算法[J].計算機應用研究,2013,30(1):249-251.

Dynamic tracking algorithm for WSNs sink node based on

UKF and regional cross localization*YAO Yi-xiang1,3, XIE Jun-yuan1,2

(1.Department of Computer Science and Technology,Nanjing University,Nanjing 210093, China; 2.National Key Laboratory for Novel Technology,Nanjing 210093,China; 3.School of Mathematics and Information Technology,Nanjing Xiaozhuang University,Nanjing 211100,China)

In order to improve wireless sensor networks(WSNs) lifetime,research on target tracking method in WSNs,and propose an unscented Kalman filtering(UKF)-based WSNs sink node dynamic tracking algorithm,in order to realize high efficient and energy-saving resource management and utilization mode.Firstly,use UKF algorithm to predict next position of target node,and then through the four circle regional positioning algorithm of cross locationing,so as to locally and accurately locate location area of sink node.The experimental results show that the dynamic prediction localization algorithm for sink node can effectively shorten distance between data transmission sensor and sink node,and reduce hop count, so as to achieve load balancing and energy consumption reducing effect.

WSNs; unscented Kalman filtering(UKF); regional cross localization; sink node; dynamic tracking

2014—08—15

國家自然科學基金資助項目(60721002, 60875038); 教育部重點研究計劃資助項目(108151)

10.13873/J.1000—9787(2015)04—0123—04

TP 18

A

1000—9787(2015)04—0123—04

姚依翔(1979-),男,江蘇泰興人,博士研究生,高級工程師,主要研究領域為逆向工程、組織網絡和人工智能。