基于OpenSees的RPC橋墩擬靜力數(shù)值模擬與參數(shù)分析

任 亮，方 志，王 誠

(1.湖南大學(xué) 土木工程學(xué)院，湖南 長沙 410082；2.華東交通大學(xué) 土建學(xué)院，江西 南昌 330013)

作為一種新型建筑材料，活性粉末混凝土(簡稱RPC)具有抗壓強度高、韌性良好和耐久性能優(yōu)異等優(yōu)點。由于混合料全部采用細骨料，RPC在長期荷載作用下徐變較小，而特殊的養(yǎng)護環(huán)境(熱養(yǎng)護)使RPC幾乎沒有收縮[1，2]，因此適合做大跨度橋梁的橋墩結(jié)構(gòu)。但目前國內(nèi)外對RPC材料在橋梁工程中的應(yīng)用研究還較少，尤其是構(gòu)件抗震性能方面研究還比較薄弱，已有研究主要集中在無軸力和常軸力作用下RPC構(gòu)件擬靜力試驗研究[3，4]。在地震荷載作用下，橋梁墩柱通常是受力最敏感也是最易破壞的結(jié)構(gòu)構(gòu)件，其滯回耗能特性在一定程度上決定了橋梁的整體抗震能力。因此，基于有限的擬靜力試驗結(jié)果較可靠模擬RPC構(gòu)件在反復(fù)荷載作用下的非線性滯回特性具有重要意義。

OpenSees全稱Open System for Earthquake Engineering Simulation，是由美國太平洋地震工程研究中心、加州大學(xué)伯克利分校等共同開發(fā)并用于巖土和結(jié)構(gòu)方面地震模擬的開放式系統(tǒng)。該系統(tǒng)具有豐富的材料和單元類型，包含大量求解算法，其源代碼的開放性使系統(tǒng)更易于改進和協(xié)同開發(fā)，目前已引起國內(nèi)外研究人員的關(guān)注和重視[4-7]。但RPC作為一種新型超高性能混凝土，在OpenSees材料庫中目前尚無材料本構(gòu)關(guān)系。為應(yīng)用OpenSees既有材料本構(gòu)關(guān)系模擬RPC材料，本文以3個常軸力作用下的大比例RPC橋墩水平反復(fù)加載滯回試驗結(jié)果為依據(jù)，通過選取OpenSees中適當(dāng)?shù)牟牧媳緲?gòu)關(guān)系和單元類型對RPC橋墩的滯回特性進行數(shù)值模擬，并在此基礎(chǔ)上運用OpenSees分析軸壓比、縱筋率和水平荷載加載方向等參數(shù)對RPC橋墩延性抗震性能的影響。

1 RPC橋墩擬靜力試驗

1.1 試驗概述

為探討RPC橋墩在地震作用下的抗震性能，對3個常軸力作用下的RPC橋墩試件施加低周水平反復(fù)荷載，研究加載方向?qū)PC橋墩抗震性能的影響。圖1為試件截面尺寸和配筋情況，其中縱筋和箍筋分別采用HRB400和HRB335熱軋鋼筋。表1為試件各參數(shù)值。

圖1 試件截面尺寸和配筋(單位：mm)

試驗加載裝置如圖2所示。水平力加載通過最大水平力為500 kN、最大水平位移為600 mm的水平作動器施加；豎向力通過放置在試件頂部加載橫梁上的兩個中空液壓千斤頂對稱張拉豎向高強鋼棒來施加，加載極值為2 000 kN。考慮到擬靜力試驗加載過程中高強鋼棒在軸向力作用下自身可能產(chǎn)生彎曲，導(dǎo)致橋墩試件偏心受壓，為消除其影響，在高強鋼棒底部設(shè)計一個可以自由轉(zhuǎn)動的單向鉸來保證加載過程中高強鋼棒和橫梁隨墩帽同時轉(zhuǎn)動。試驗加載采用位移循環(huán)控制方式，相應(yīng)加載制度如圖3所示。

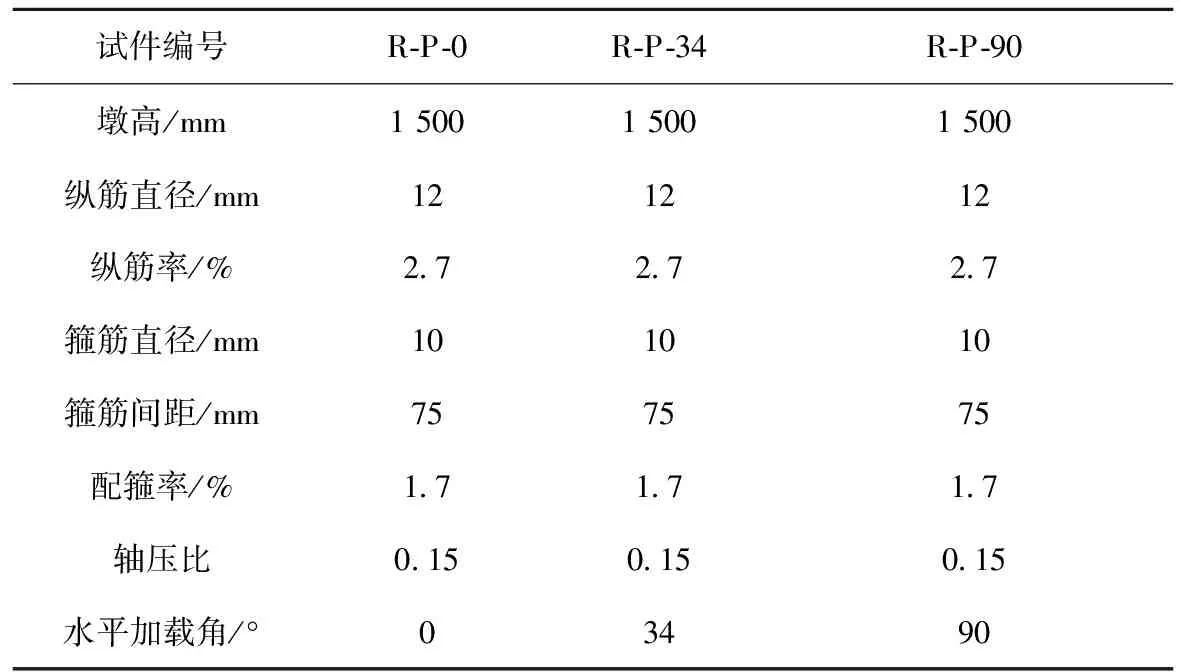
表1 試件參數(shù)

注：試件編號中R代表RPC，P代表橋墩(Pier)，數(shù)字代表截面長邊與加載方向之間的夾角(°)。

圖2 試驗加載裝置圖(單位：mm)

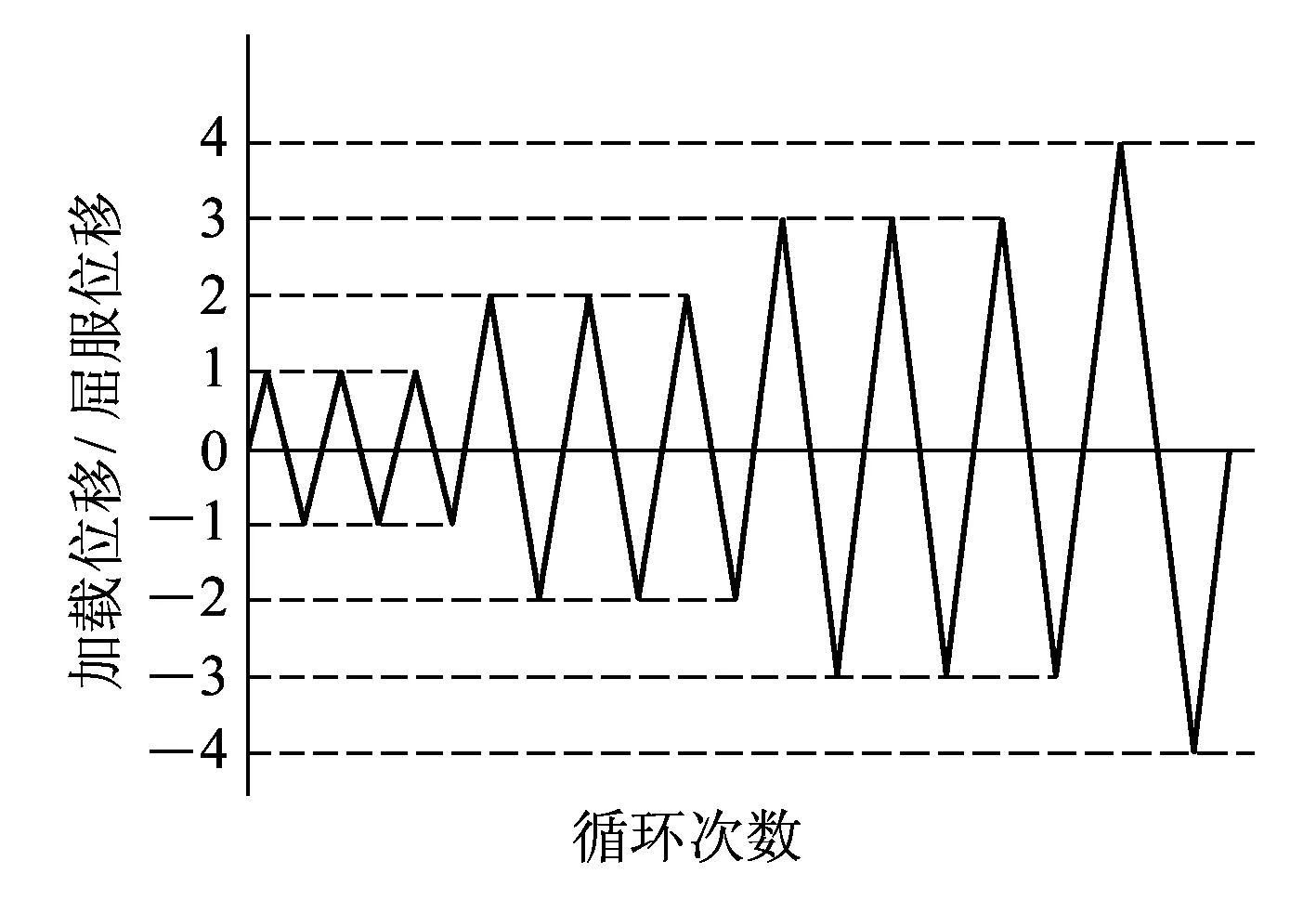
圖3 加載制度示意圖

1.2 試件破壞形態(tài)

RPC橋墩試件在擬靜力荷載作用下首先在根部出現(xiàn)局部水平微裂縫，隨著水平力的持續(xù)增加，RPC橋墩試件根部不斷出現(xiàn)新的微裂縫，而根部原有裂縫的長度和寬度也迅速發(fā)展，并逐漸貫通形成肉眼可見的斜向裂縫；與此同時，在RPC橋墩試件根部開裂處可以明顯觀察到鋼纖維相繼被拉斷，部分甚至被拔出。最終破壞時RPC橋墩試件根部混凝土被壓碎并脫落，根部裸露的縱筋出現(xiàn)明顯屈服，其中對角軸加載的RPC橋墩試件R-P-34還出現(xiàn)部分縱筋被拉斷的現(xiàn)象。圖4為3個試件最終破壞形態(tài)。

(a)R-P-0

(b)R-P-34

(c)R-P-90圖4 試件破壞現(xiàn)象

1.3 骨架曲線

圖5為3個RPC橋墩試件在低周水平反復(fù)荷載作用下的骨架曲線對比，從圖5可以看出：

圖5 試件骨架曲線對比

(1)RPC橋墩試件在不同的水平荷載加載方向時，骨架曲線均表現(xiàn)出較明顯上升段、強化段和下降段；

(2)主軸加載試件R-P-0和試件R-P-90骨架曲線經(jīng)過極值點荷載后均出現(xiàn)明顯的強度下降平臺，說明其在反復(fù)荷載作用下具有較好的延性；對角軸加載試件R-P-34骨架曲線經(jīng)過極值點荷載后有快速下降的趨勢，延性較其余兩試件差，說明水平荷載加載方向?qū)PC橋墩試件延性抗震性能有較大影響。

2 材料本構(gòu)關(guān)系及其擬合

2.1 RPC本構(gòu)關(guān)系

考慮到目前有約束RPC材料應(yīng)力-應(yīng)變關(guān)系無相關(guān)文獻，為此選用無約束RPC材料應(yīng)力-應(yīng)變關(guān)系，相應(yīng)的受壓本構(gòu)表達式為[8]

( 1 )

式中：ε和σc分別表示壓應(yīng)變和壓應(yīng)力；ε0和εu分別表示峰值點應(yīng)變和極值點應(yīng)變，其值分別取3 500×10-6和4 500×10-6；fc為棱柱體抗壓強度；ξ=ε/ε0；n=E0/Es，其中E0表示初始彈性模量，Es表示峰值點割線模量。E0可由式( 2 )計算求得。

( 2 )

RPC受拉應(yīng)力-應(yīng)變關(guān)系考慮鋼纖維的抗裂效應(yīng)，其表達式為[9]

( 3 )

式中：εt為拉應(yīng)變；σt為εt對應(yīng)拉應(yīng)力；εt0為峰值點對應(yīng)拉應(yīng)變；εtu為極限拉應(yīng)變，且εtu=2εt0；ft為極限抗拉強度，其值為RPC立方體抗壓強度的1/23.6；Ec為抗拉彈性模量，其值與初始彈性模量E0一致。

2.2 RPC本構(gòu)關(guān)系在OpenSees中的擬合

考慮到OpenSees系統(tǒng)中Concrete02材料(采用Scott、Park等人修正的Kent-Park混凝土本構(gòu)模型)能較好模擬混凝土壓彎構(gòu)件在反復(fù)荷載作用下的滯回特性，本文選用Concrete02本構(gòu)關(guān)系對RPC本構(gòu)關(guān)系進行擬合，相應(yīng)的應(yīng)力-應(yīng)變滯回關(guān)系如圖6所示。

圖6 Concrete 02應(yīng)力-應(yīng)變滯回關(guān)系

不考慮箍筋約束時，受壓骨架曲線為

( 4 )

其中

( 5 )

式中：Zm為骨架曲線下降段對應(yīng)斜率；εc為壓應(yīng)變；σc為εc對應(yīng)壓應(yīng)力；fc為混凝土棱柱體抗壓強度；ε0為峰值點壓應(yīng)變；εu為極限壓應(yīng)變；sh和h′分別表示箍筋間距和從箍筋外邊緣算起的核心混凝土寬度；ρs為體積配箍率。

考慮到Concrete02中Zm為輸入項，因此在OpenSees中可通過調(diào)整Zm值擬合RPC材料應(yīng)力-應(yīng)變關(guān)系，其中Zm取值必須保證峰值點壓應(yīng)變和極限壓應(yīng)變間RPC應(yīng)力-應(yīng)變曲線和擬合曲線相關(guān)度不低于95%，相關(guān)系數(shù)可通過Excel中的相關(guān)函數(shù)CORREL確定。

受拉骨架曲線為

( 6 )

式中：σt為拉應(yīng)力；εt為拉應(yīng)變；εt0為峰值點拉應(yīng)變；Ec為骨架曲線受拉初始彈性模量；Ets為骨架曲線受拉軟化段曲率；ft為混凝土極限抗拉強度。

現(xiàn)取ε0=0.003 5，εu=0.004 5，εt0=1.34×10-4，εtu=2.68×10-4，fc=140 MPa，ft=6 MPa，Ec=Ets=44.8 GPa，通過調(diào)整Zm值得到如圖7所示RPC材料本構(gòu)與Concrete02擬合本構(gòu)對比。

圖7 RPC材料與Concrete02擬合本構(gòu)對比

注：圖中應(yīng)力拉為負，壓為正；應(yīng)變拉為負，壓為正。

從圖7可以看出，Concrete02與RPC受壓骨架曲線上升段能較好吻合，下降段在極限壓應(yīng)變之前兩者基本吻合；受拉骨架曲線在上升段兩者吻合較好，下降段Concrete02材料為直線下降，而RPC材料在經(jīng)過峰值點拉應(yīng)變后為水平直線，但考慮到RPC材料以受壓為主，因此與Concrete02受拉骨架曲線對比，下降段存在的偏差可以接受。

2.3 鋼筋本構(gòu)關(guān)系

考慮到試件在低周水平反復(fù)加載后期出現(xiàn)明顯的強度和剛度退化、試件根部縱筋出現(xiàn)屈服甚至拉斷的現(xiàn)象，選用OpenSees中的Steel02材料[10]對RPC橋墩非線性滯回特性進行模擬，相應(yīng)的應(yīng)力-應(yīng)變滯回關(guān)系如圖8所示。

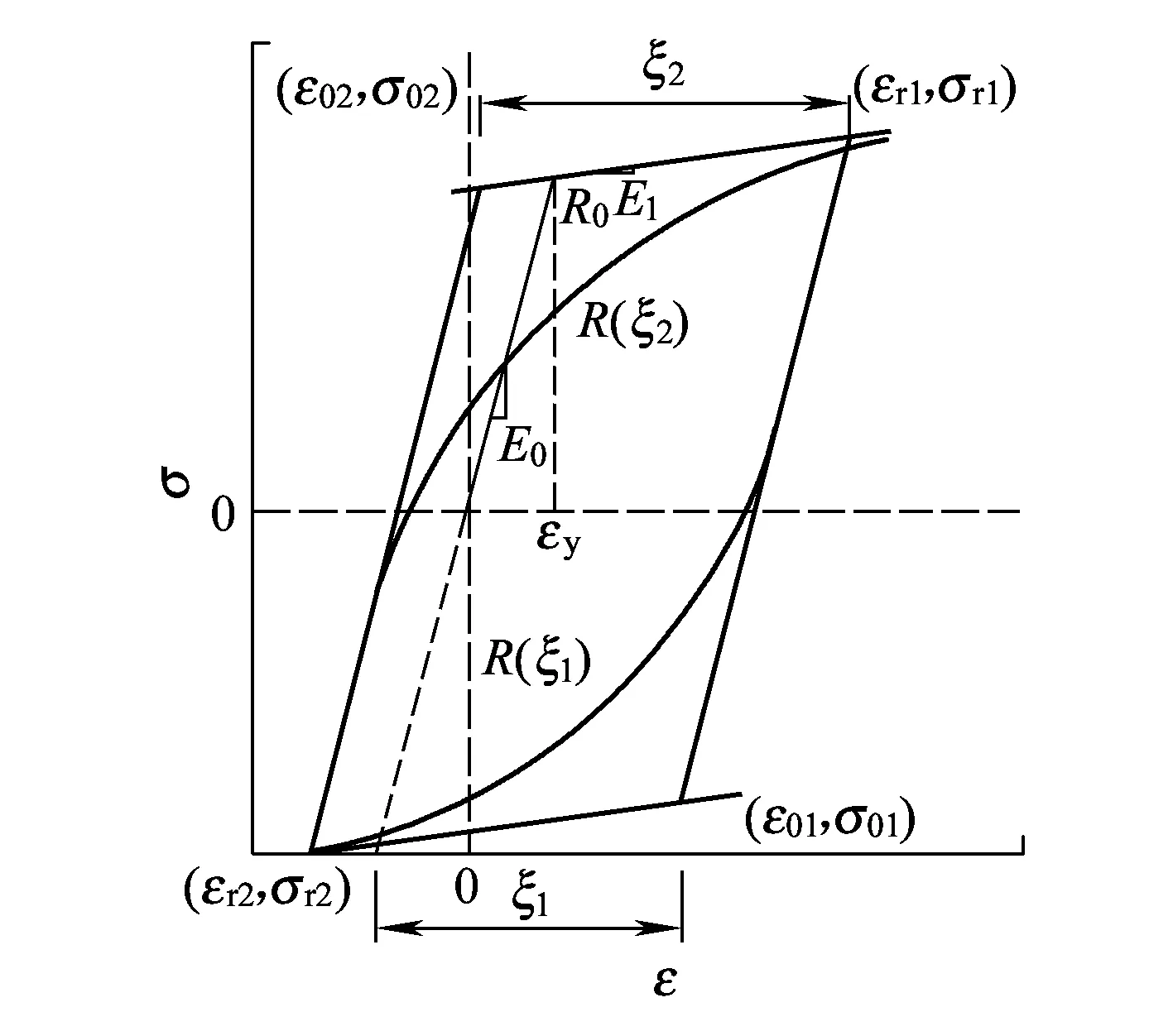
圖8 Steel02應(yīng)力-應(yīng)變滯回關(guān)系

Steel02采用Menegotto-Pinto鋼筋模型，相應(yīng)的模型表達形式為

( 7 )

其中

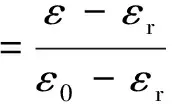
( 8 )

( 9 )

(10)

式中：ε0和εr分別表示鋼筋的屈服應(yīng)變和雙線性包絡(luò)線反向點處鋼筋應(yīng)變；σ0和σr分別表示鋼筋的屈服應(yīng)力和雙線性包絡(luò)線反向點處鋼筋應(yīng)力；a1和a2為材料常數(shù)；b=E1/E0，其中E0為鋼筋初始彈性模量，E1為鋼筋硬化模量；ξ為上一級循環(huán)對應(yīng)的塑性應(yīng)變絕對值；R0為考慮包辛格效應(yīng)的鋼筋常數(shù)。

3 考慮墩底縱筋滑移的滯回分析模型

基于上述擬合的RPC本構(gòu)關(guān)系和Steel02鋼筋本構(gòu)關(guān)系，應(yīng)用非線性梁柱單元模擬RPC橋墩試件的非線性行為，應(yīng)用零長度單元模擬RPC橋墩試件根部鋼筋與活性粉末混凝土間的黏結(jié)-滑移效應(yīng)，本文建立考慮墩底縱筋滑移的滯回分析模型，如圖9所示。

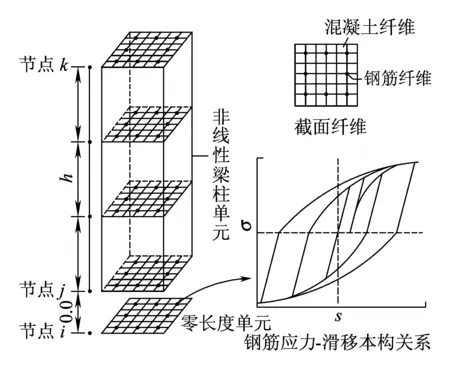
圖9 考慮墩底縱筋滑移的滯回分析模型

圖9中非線性梁柱單元和零長度單元均采用截面纖維模型，為準(zhǔn)確描述構(gòu)件沿高度方向柔度的變化，首先將構(gòu)件沿高度方向設(shè)置多個以力插值函數(shù)為基礎(chǔ)的積分控制點，然后根據(jù)鋼筋和混凝土應(yīng)力-應(yīng)變關(guān)系迭代求得各纖維單元的剛度和抗力，最后通過Gauss-Lobatto積分計算出截面所有單元的剛度矩陣和抗力矩陣。零長度單元采用同一個位置的2個節(jié)點(圖9中的節(jié)點i和節(jié)點j)來表示，節(jié)點對應(yīng)的截面與非線性梁柱單元截面具有相同的混凝土和鋼筋配置，且混凝土和鋼筋的纖維劃分一致；不同之處在于非線性梁柱單元截面鋼筋纖維的本構(gòu)關(guān)系為前述Steel02應(yīng)力-應(yīng)變關(guān)系，零長度單元截面鋼筋纖維的本構(gòu)關(guān)系為鋼筋的應(yīng)力-滑移(σ-s)關(guān)系。由于目前尚無鋼筋在活性粉末混凝土中的應(yīng)力-滑移關(guān)系文獻，本文參考文獻[11]中鋼筋應(yīng)力-滑移關(guān)系和定參方法，其中的滑移量s(如鋼筋屈服時對應(yīng)的滑移)根據(jù)UEDA[12]等完成的梁柱內(nèi)部鋼筋錨固性能試驗數(shù)據(jù)經(jīng)回歸分析求得，滯回規(guī)則根據(jù)LIN[13]完成的具有足夠錨固長度的鋼筋反復(fù)加載滑移規(guī)律來確定，如圖9所示。其中的應(yīng)力-滑移骨架曲線假定關(guān)于原點對稱，且反復(fù)加載過程中，卸載剛度按初始剛度取值，加載路徑由以下各式確定

σ=σ*·σmaxσ>0

(11)

σ=σ*·σminσ<0

(12)

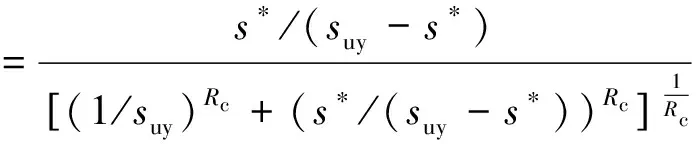
(13)

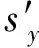
(14)

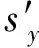
(15)

(16)

4 RPC橋墩擬靜力數(shù)值模擬

基于考慮墩底縱筋滑移的滯回分析模型，本文對3個RPC橋墩試件在常軸力作用下的低周水平反復(fù)荷載試驗進行數(shù)值模擬，圖10和圖11分別為試件骨架曲線和滯回曲線試驗值與計算值對比。

(a)R-P-0

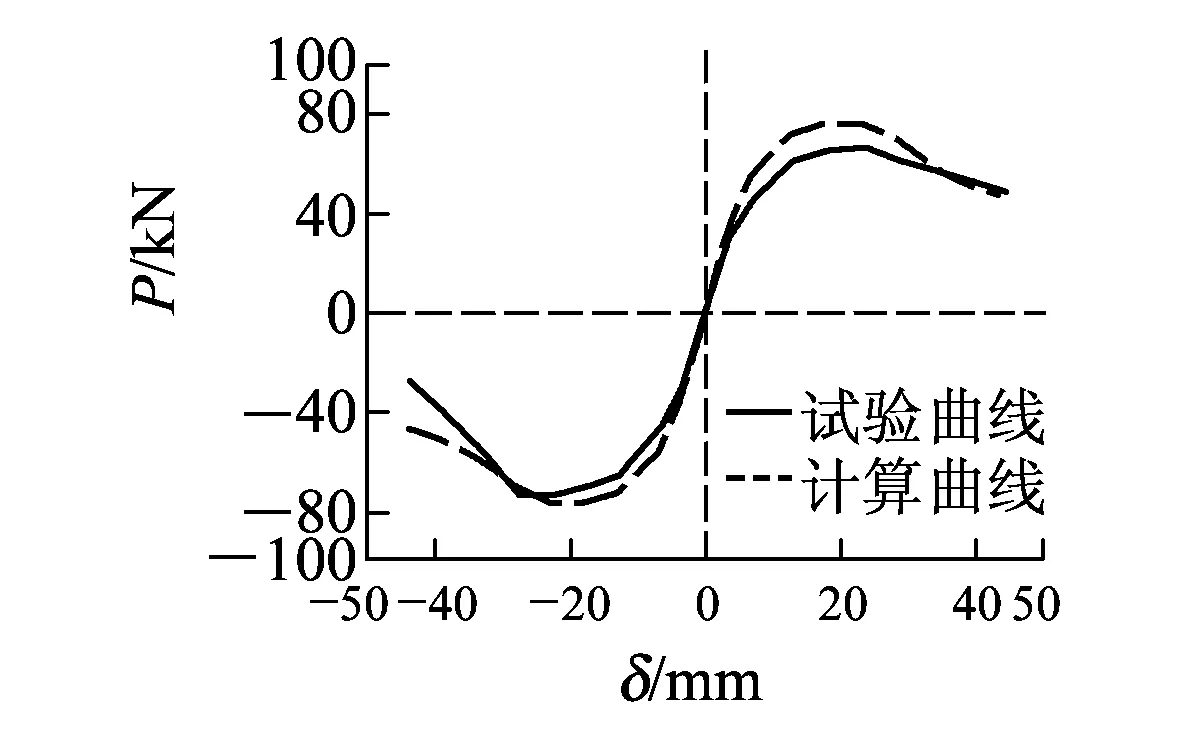
(b)R-P-34

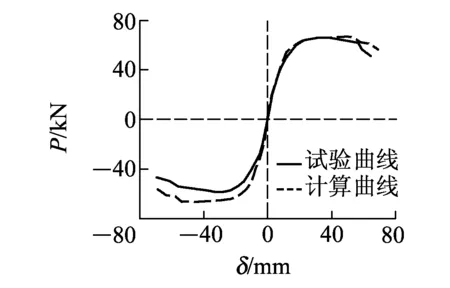
(c)R-P-90圖10 骨架曲線對比

(a)R-P-0試驗曲線

(b)R-P-34試驗曲線

(c)R-P-90試驗曲線

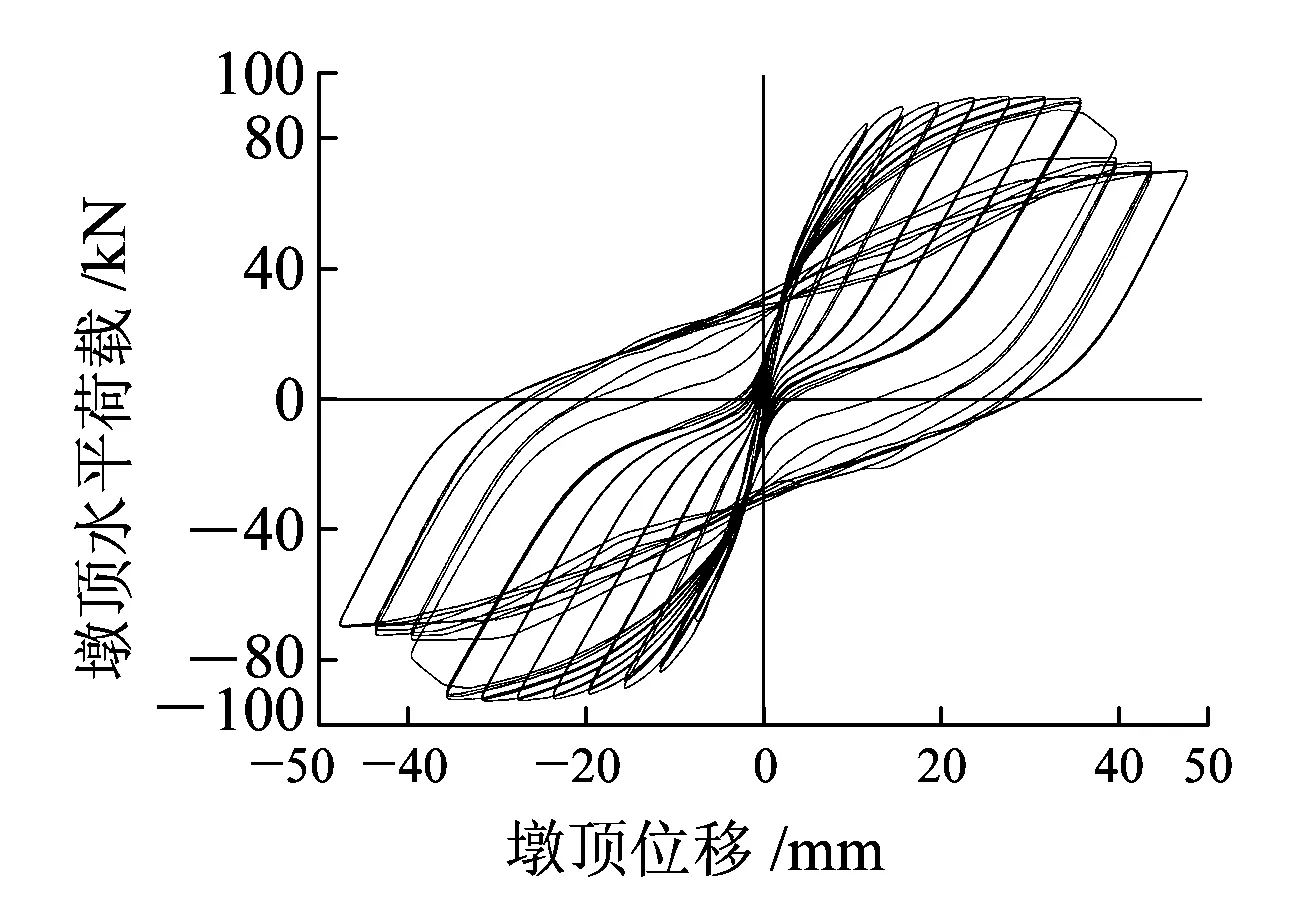
(d)R-P-0計算曲線

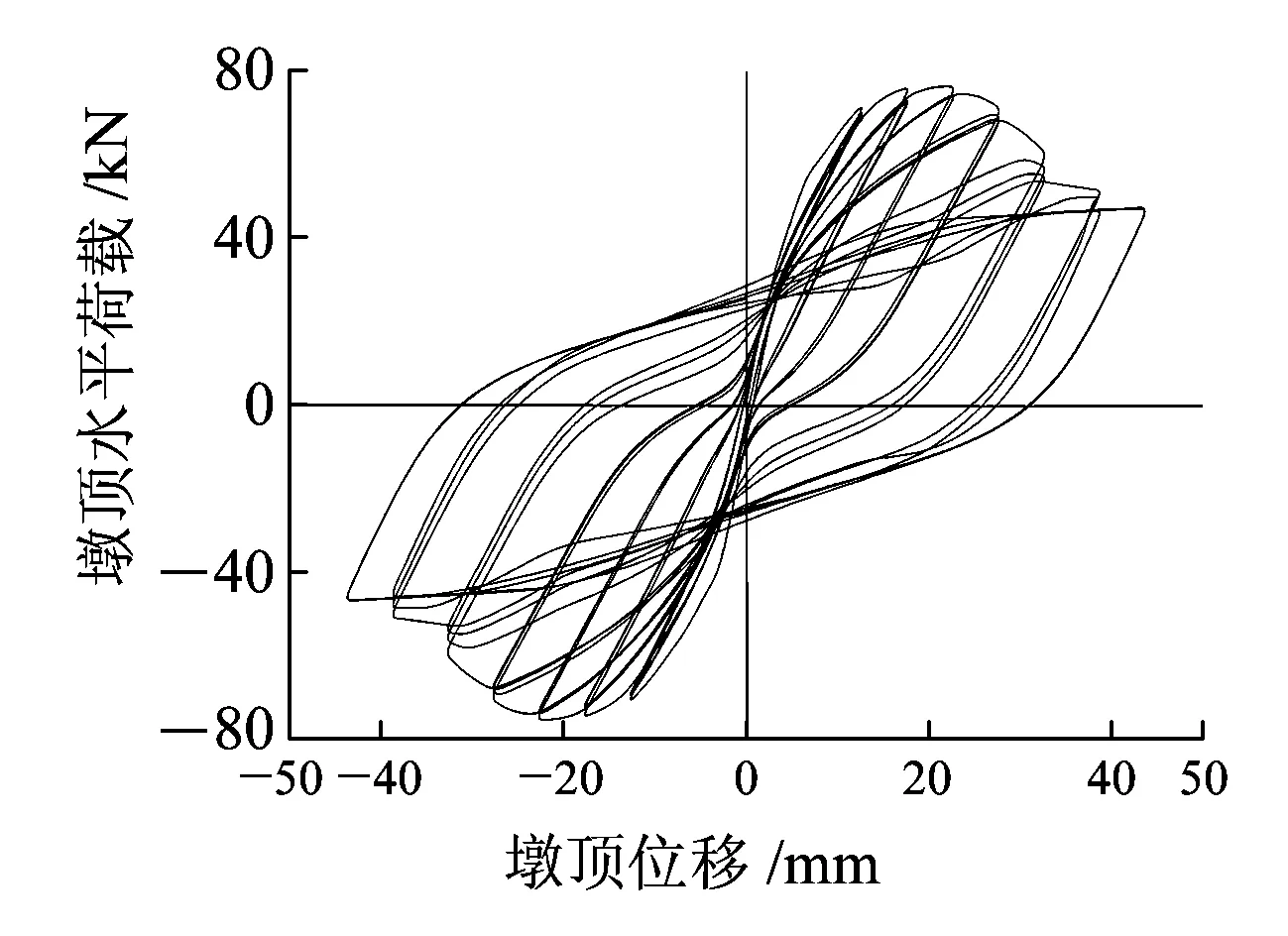
(e)R-P-34計算曲線

(f)R-P-90計算曲線圖11 滯回曲線對比

從圖10可以看出，2組曲線形狀相似但試驗曲線峰值點荷載偏小，這是由于RPC橋墩試件在反復(fù)荷載作用下已產(chǎn)生損傷，在一定程度上降低了結(jié)構(gòu)承載力；2組曲線開裂前吻合較好，開裂后存在偏差，其中試件R-P-34由于未考慮扭轉(zhuǎn)變形影響偏差最大。

從圖11可以看出，3個RPC橋墩試件在水平反復(fù)荷載作用下的滯回曲線上升段和強度退化均得到較好模擬，但經(jīng)過峰值點荷載后試件均出現(xiàn)不同程度的快速卸載現(xiàn)象，這是由于Concrete02本構(gòu)下降段為線性下降；由于數(shù)值模擬未考慮扭轉(zhuǎn)變形的影響，試件R-P-34模擬效果較試件R-P-0和試件R-P-90差。

因此，綜合考慮計算值與試驗值的差異性后，本文應(yīng)用OpenSees中的Concrete02本構(gòu)關(guān)系和Steel02本構(gòu)關(guān)系，結(jié)合非線性梁柱單元和零長度單元能較好模擬RPC橋墩的骨架曲線和滯回曲線，并能反映試件在反復(fù)加載過程中強度和剛度的退化。

5 參數(shù)分析

為進一步探討RPC橋墩在擬靜力荷載作用下的延性抗震性能，本文應(yīng)用上述方法分析軸壓比、縱筋率和水平荷載加載方向等參數(shù)對RPC橋墩位移延性系數(shù)(極限位移與屈服位移比值)的影響。分析時試件高度、截面尺寸與原RPC橋墩相同，為方便表述，將加載角0°方向稱為截面強軸，加載角90°方向稱為截面弱軸。

5.1 軸壓比

軸壓比是影響橋墩延性的重要因素之一。圖12是縱筋率分別為1.9%、2.7%和3.7%時位移延性系數(shù)隨軸壓比變化的曲線(加載方向按強軸考慮)。

圖12 位移延性系數(shù)隨軸壓比的變化

從圖12可以看出，在軸壓比小于0.2時，位移延性系數(shù)隨軸壓比的增大下降較快；當(dāng)軸壓比大于0.2時，位移延性系數(shù)隨軸壓比的增加緩慢降低，并逐漸接近1。這說明軸壓比增加到一定程度，RPC構(gòu)件將表現(xiàn)出明顯的脆性。

5.2 縱筋率

縱筋率是影響橋墩延性的另一重要因素。圖13是軸壓比分別為0、0.1、0.2和0.3時位移延性系數(shù)隨縱筋率變化的曲線(加載方向按強軸考慮)。

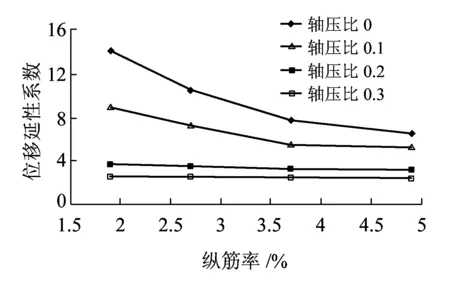
圖13 位移延性系數(shù)隨縱筋率的變化

從圖13可以看出，當(dāng)軸壓比小于0.2時，位移延性系數(shù)隨縱筋率的提高降低明顯，這是由于軸壓比較小時，橋墩發(fā)生適筋破壞，雖然墩的屈服位移或屈服曲率隨縱筋率提高而增加，但墩的極限位移變化較小，降低了墩的延性；當(dāng)軸壓比大于0.2時，RPC構(gòu)件表現(xiàn)出明顯的脆性，位移延性系數(shù)隨縱筋率的提高無明顯改變。

5.3 水平荷載加載方向

從前述擬靜力試驗結(jié)果可以看出，水平加載角對RPC橋墩延性影響較大，為此選取0°、15°、30°、45°、60°、75°和90°水平加載角(對角軸位置和可能的不利加載位置)進行分析。圖14分別為不同軸壓比和縱筋率時位移延性系數(shù)隨水平荷載加載方向變化的曲線。

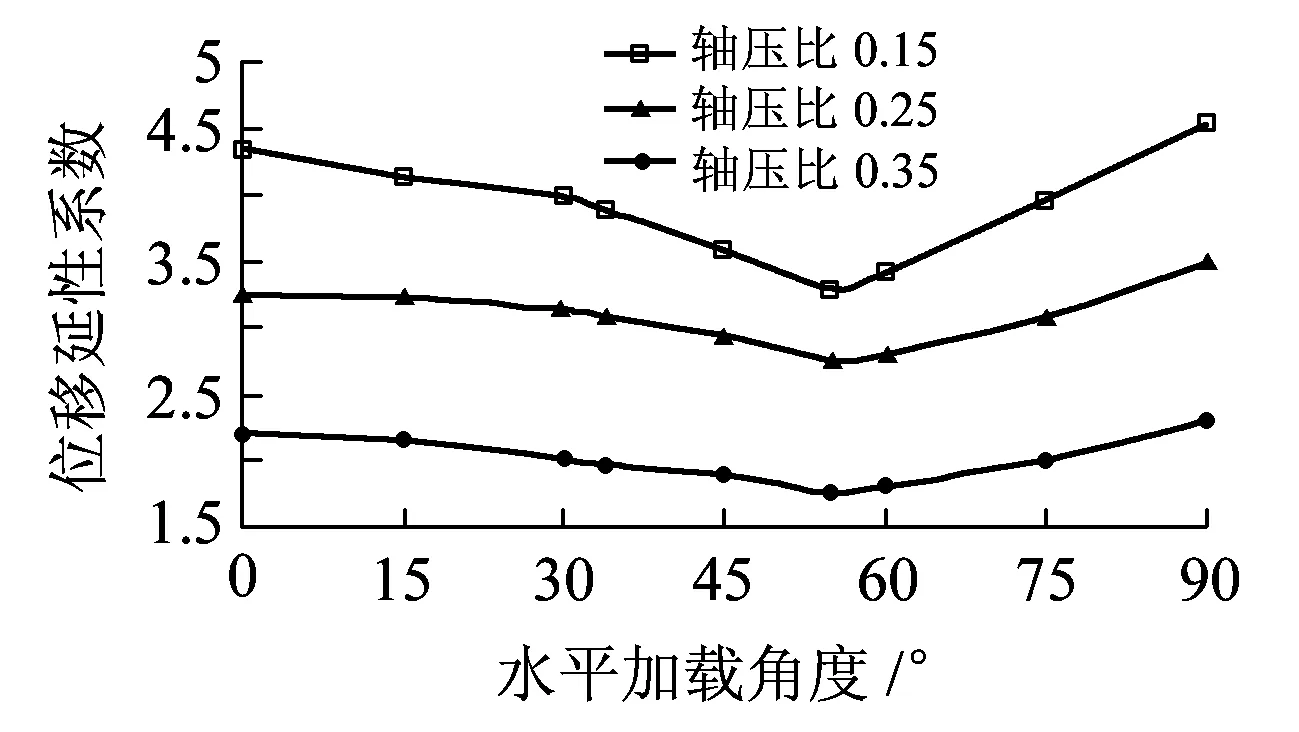
(a)不同的軸壓比(縱筋率2.7%)

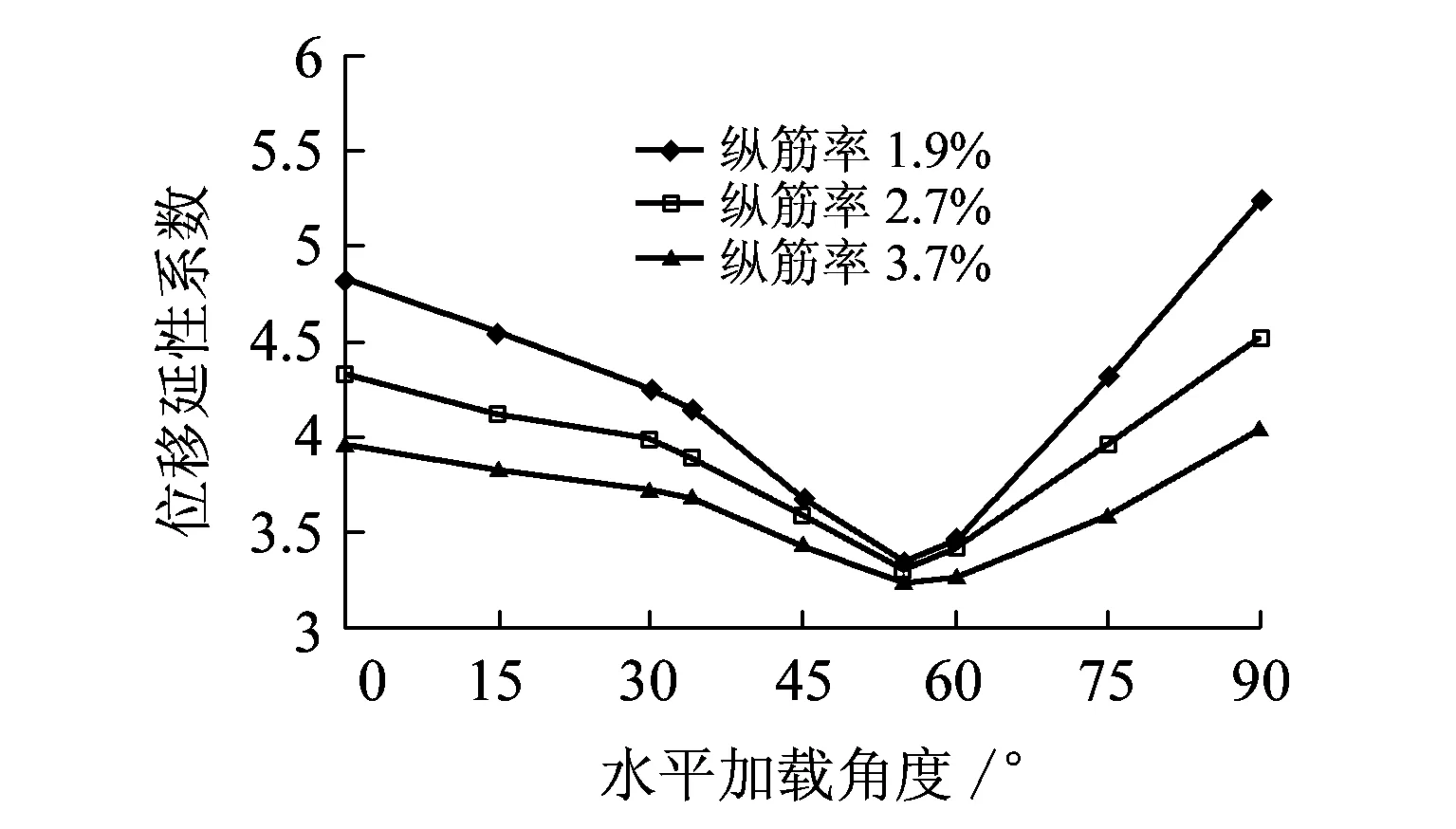
(b)不同的縱筋率(軸壓比0.15)圖14 位移延性系數(shù)隨水平加載方向的變化

從圖14可以看出，RPC橋墩位移延性系數(shù)隨水平加載方向的變化而改變，且在主軸(強軸和弱軸)之間存在一個最不利的加載方向角(約為55°)，該加載方向不隨軸壓比和縱筋率的變化而改變，大致與對角軸垂直。這是由于在該加載方向縱筋之間受力不均勻性最大，導(dǎo)致靠近墩角的受力縱筋在荷載作用下最易屈服，且在屈服后鋼筋迅速進入強化階段并最終被拉斷，試件表現(xiàn)出明顯的脆性破壞特征，因而延性最低。

6 結(jié)論

本文基于OpenSees中既有材料本構(gòu)關(guān)系和單元類型對RPC橋墩進行擬靜力數(shù)值模擬和參數(shù)分析，得到以下結(jié)論：

(1)基于適當(dāng)?shù)膮?shù)選取，運用OpenSees中Concrete02本構(gòu)關(guān)系能較好擬合RPC本構(gòu)關(guān)系。

(2)應(yīng)用OpenSees中既有本構(gòu)關(guān)系和單元類型建立的考慮墩底縱筋滑移的滯回分析模型能較好模擬RPC箱型橋墩的骨架曲線及滯回曲線，并能反映構(gòu)件在反復(fù)加載過程中強度和剛度的退化。

(3)橋墩的位移延性系數(shù)隨軸壓比的增加和縱筋率的提高而降低，隨水平加載方向的變化而改變，且在主軸之外存在一個最不利加載方向，該方向不隨軸壓比和縱筋率的變化而改變，大致與對角軸垂直。

參考文獻：

[1]RICHARD P,CHEYREZY M.Composition of Reactive Powder Concrete[J].Cement and Concrete Research,1995,25(7):1501-1511.

[2]BONNEAU O,LACHEMI M.Mechanical Properties and Durability of Two Industrial Reactive Powder Concrete[J].ACI Material Journal,1997,94(4):286-290.

[3]郝文秀,鐘鐵毅,趙冠遠.活性粉末混凝土空心橋墩恢復(fù)力模型試驗研究[J].鐵道學(xué)報,2011,33(8):89-93.

HAO Wen-xiu,ZHONG Tie-yi,ZHAO Guan-yuan.Experimental Study on the Restoring Force Model of Reactive Powder Concrete Hollow Piers[J].Journal of the China Railway Society,2011,33(8):89-93.

[4]王誠.活性粉末混凝土箱型橋墩抗震性能試驗研究[D].長沙：湖南大學(xué)，2010:48-50.

[5]王瑾,蔡新江,田石柱.基于OpenSees的CFRP加固RC短柱抗震性能數(shù)值模擬[J].世界地震工程,2009,25(4):108-111.

WANG Jin,CAI Xin-jiang,TIAN Shi-zhu.Numerical Simulation on Seismic Behavior of CFRP Retrofitted RC Short Column Based on OpenSees[J].World Earthquake Engineering,2009,25(4):108-111.

[6]朱雁茹,郭子雄.基于OpenSees的SRC柱低周往復(fù)加載數(shù)值模擬[J].廣西大學(xué)學(xué)報：自然科學(xué)版,2010,35(4):555-559.

ZHU Yan-ru,GUO Zi-xiong.Numerical Simulation of SRC Column under Low Cyclic Loading Based on OpenSees[J].Journal of Guangxi University:Nature Science,2010,35(4):555-559.

[7]李貴乾,鄭罡,高波.基于OpenSees的鋼筋混凝土橋墩擬靜力試驗數(shù)值分析[J].世界地震工程,2011,27(1):110-114.

LI Gui-qian，ZHENG Gang，GAO Bo.Numerical Analysis for Pseudo-static Tests of Reinforced Concrete Bridge Columns Based on OpenSees[J].World Earthquake Engineering,2011,27(1):110-114.

[8]單波.活性粉末混凝土基本力學(xué)性能的試驗與研究[D].長沙：湖南大學(xué)，2002:35-50.

[9]原海燕,安明喆, 賈方方,等.活性粉末混凝土軸拉性能試驗研究[J].工程力學(xué)(S1),2011,28(1):141-144.

YUAN Hai-yan,AN Ming-zhe,JIA Fang-fang,et al.Experimental Research on Uniaxial Tensile Performance of Reactive Powder Concrete[J].Engineering Mechanics(S1),2011,28(1):141-144.

[10]MAZZONI S,MCKENNA F,SCOTT M H,et al.OpenSees Command Language Manual[Z].Berkeley:PEER,University of California,2007.

[11]ZHAO J,SRITHARAN S.Modeling of Strain Penetration Effects in Fiber-based Analysis of Reinforced Concrete Structures[J].ACI Structural Journal,2007,104(2):133-141.

[12]UEDA T,LIN I,HAWKINS N M,et al.Beam Bar Anchorage in Exterior Column-beam Connections[J].ACI Structural Journal,1986,83(3):412-422.

[13]LIN I.Anchorage Characteristics for Reinforcing Bars Subjected to Reversed Cyclic Loading[D].Seattle:University of Washington,1981.