不同軌底坡下地鐵車輛輪軌型面匹配的靜態接觸分析

陶功權， 溫澤峰， 陸文教， 金學松

(西南交通大學 牽引動力國家重點實驗室， 四川 成都 610031)

軌底坡作為軌道結構的一個重要參數，對輪軌型面匹配具有非常重要的影響。1965年以前我國國鐵軌底坡為1/20，1965年改為現行的1/40[1]，文獻[2]明確規定地鐵鋼軌軌底坡宜為1/40～1/30。首都機場線首次采用1/20軌底坡，輪軌匹配關系良好，輪軌接觸點基本位于車輪及鋼軌踏面中心[3]。我國地鐵車輛車輪踏面大部分采用LM型面。隨著國外地鐵車輛的引進，也有不少車輛采用歐洲標準的S1002型面和德國標準的DIN5573型面。針對不同的地鐵車輪型面，軌底坡的取值值得深入研究。

沈鋼[4]等研究發現，在曲線軌道上設置內外軌合理的軌底坡配比能夠增加車輛曲線通過時的滾動圓半徑差，改善輪對的自導向性能，減輕鋼軌的側磨。為了減緩曲線鋼軌的側磨，周亮[5]在上海軌道交通1號線進行了大量的試驗研究，試驗結果表明軌底坡的取值對鋼軌側磨具有重要影響。鄧建輝等[6]通過試驗研究發現，不同輪軌型面匹配條件下設置合理的軌底坡能夠降低鋼軌的滾動接觸疲勞損傷。軌底坡對車輪踏面剝離也具有重要影響[7]。李霞等[8-9]利用三維彈性體非赫茲滾動接觸理論詳細分析了軌底坡對LM和LMA兩種型面接觸行為的影響，認為對于不同的車輪型面其最佳軌底坡并不相同。張劍等[10]從輪軌接觸幾何、非赫茲滾動接觸和動力學性能三方面分析了1/40軌底坡下地鐵車輪型面LM和S1002與60 kg/m(CHN60)鋼軌的匹配關系。 ZAKERI等[11]從動力學分析角度討論了軌底坡對輕軌線輪軌相互作用力及輪軌磨耗的影響。SADEFHI等[12]從試驗和理論兩方面評價了軌底坡對鐵路軌道幾何條件的影響，提出了一個新的包含軌底坡的軌道幾何條件評價指數。

鋼軌接觸光帶能夠直觀地反映車輛運行時的輪軌接觸狀態，接觸光帶分布是否合理在一定程度上能夠反應輪軌接觸匹配是否合理。圖1為某地鐵一直線段接觸光帶的現場照片，該地鐵車輪型面為LM。從圖1(a)可以看出，接觸光帶出現在軌距角處，車輪與鋼軌R13圓弧頻繁接觸，接觸區輪軌型面曲率半徑小，使輪軌之間產生較大接觸應力，加劇輪軌磨耗和滾動接觸疲勞，造成接觸光帶異常最可能的原因是鋼軌軌底坡設置不合理。圖1(b)中可以清晰看出光帶位于軌頂中間位置，光帶分布合理，且寬度較圖1(a)中寬。

設置合理的軌底坡能夠降低輪軌接觸應力[9-10]，減緩輪軌磨耗[4-8, 13]，降低輪軌滾動接觸疲勞發生的可能性[6-7]，改善車輛的運行穩定性和曲線通過性能。本文從輪軌接觸幾何關系和輪軌非赫茲滾動接觸理論兩方面分析我國現采用的3種地鐵車輪型面LM、S1002和DIN5573與CHN60鋼軌在不同軌底坡下的匹配關系，從靜力學分析角度尋找最優軌底坡匹配，為地鐵線路的設計、降低輪軌接觸應力和減緩地鐵輪軌磨耗和滾動接觸疲勞提供理論依據。此外，由于軌道施工存在誤差，實際軌底坡與設計軌底坡之間存在一定的差異，本文的計算分析也能夠為評估由于施工誤差造成的軌底坡不同對輪軌接觸行為的影響。

1 輪軌滾動接觸計算模型

采用跡線法計算輪軌接觸幾何參數；利用計算得到接觸幾何參數，如車輪瞬時滾動圓半徑、接觸角和側滾角等參數來計算蠕滑率；將計算得到的輪軌接觸幾何參數、蠕滑率和輪軌法向間隙等作為非赫茲滾動接觸計算的輸入量，計算輪軌接觸應力等值。從輪軌接觸幾何關系和輪軌非赫茲滾動接觸理論兩方面分析地鐵車輪型面的最優軌底坡匹配。

1.1 輪軌接觸幾何和蠕滑率計算模型

輪軌接觸幾何計算是進行輪軌匹配分析的基礎，跡線法[14]是目前求解輪軌接觸幾何關系的常用方法。本文采用跡線法確定輪軌接觸幾何參數，其具體算法和數值實現過程見文獻[14-15]。

輪對在直線鋼軌上運行時，輪軌之間的蠕滑率計算公式在略去高階小量后為[15]

( 1 )

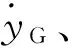
1.2 輪軌滾動接觸力學模型

本文用Kalker三維彈性體非赫茲滾動接觸理論及其數值程序CONTACT求解輪軌滾動接觸。通過將輪軌的可能接觸斑進行離散，借助Bossinesq-Cerruti公式，得到彈性輪軌三維非赫茲滾動接觸的離散形式[15-16]為

( 2 )

式( 2 )中各參數的具體含義見文獻[15]。式(2)表示彈性滾動接觸輪軌系統余能原理形式數學表達式，屬數學規劃問題的解，用數學規劃法可求解。

2 軌底坡對輪軌接觸幾何和蠕滑率的影響

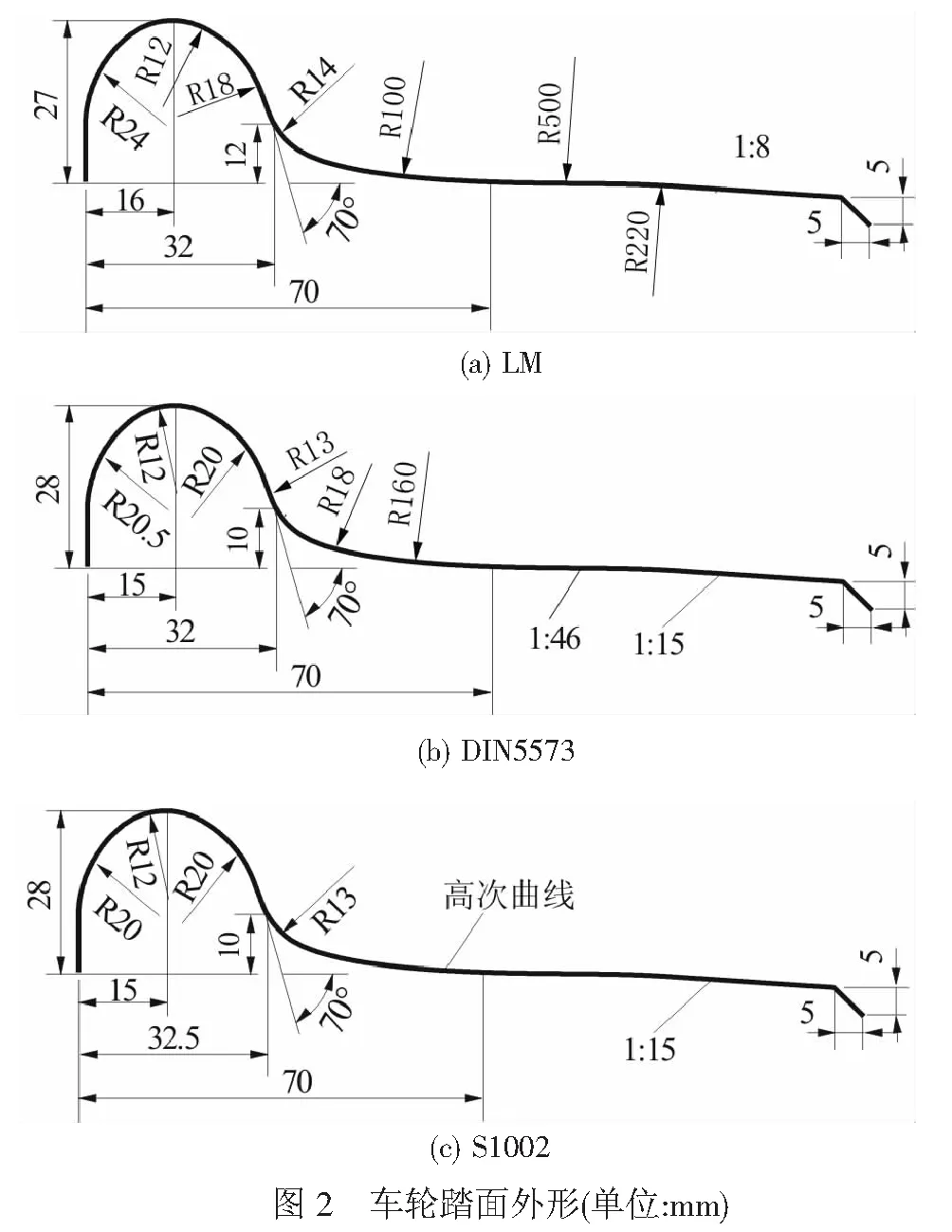
輪軌接觸幾何的計算參數：輪對內側距1 353 mm，軌距1 435 mm，車輪名義滾動圓半徑420 mm，軌底坡為1/50～1/10，輪對橫移量為 0～12 mm；輪對向左橫移，不考慮輪對的搖頭角。車輪型面為我國地鐵常用型面：LM、S1002和DIN5573，外形見圖2；鋼軌型面為CHN60。

2.1 接觸點位置

輪軌接觸點對的分布對車輪磨耗在橫向上的分布具有非常重要的影響，接觸點過于集中使車輪磨耗過于集中，對車輪的使用壽命不利[17]。

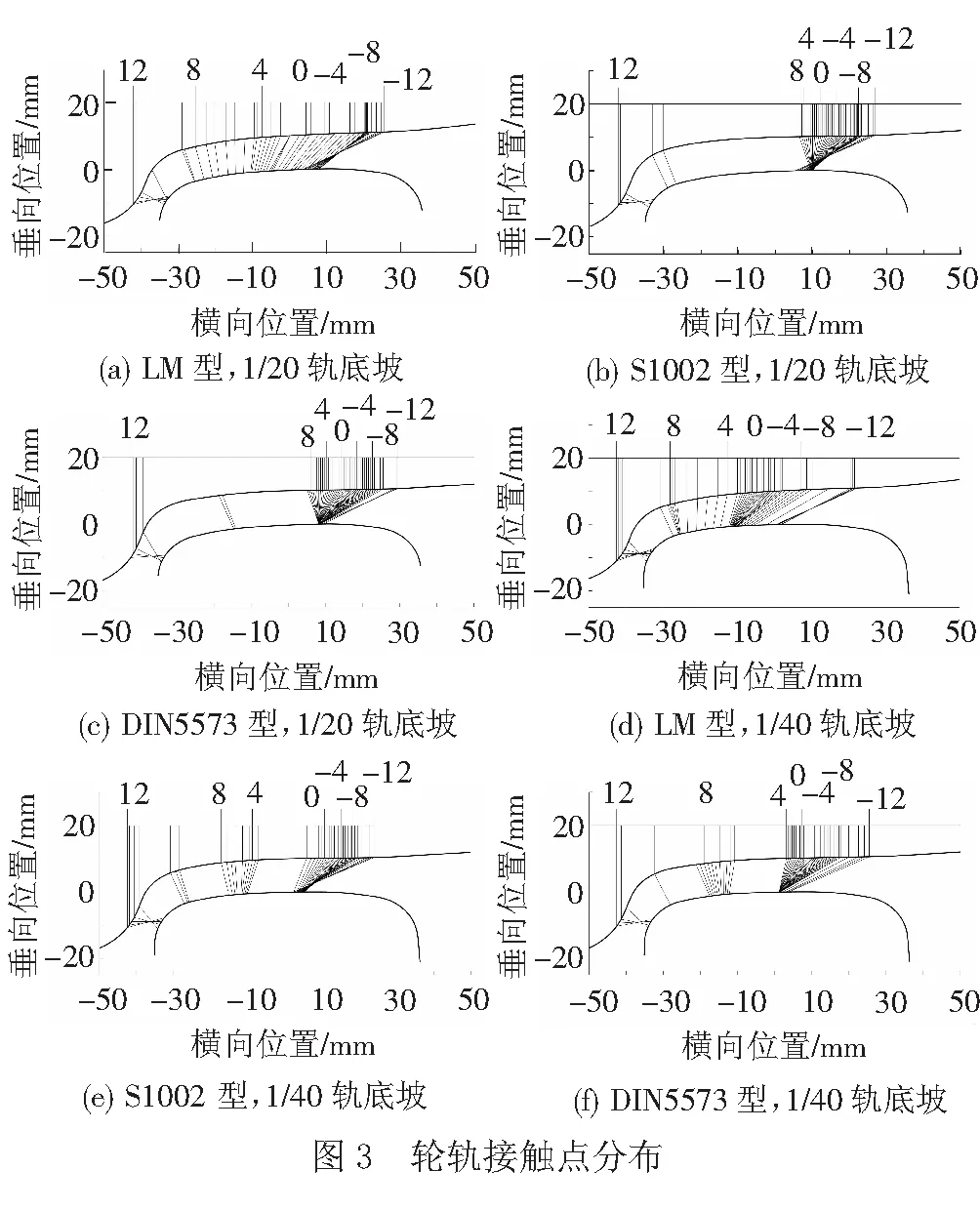
1/20和1/40軌底坡時3種車輪型面(LM、S1002和DIN5573)與CHN60鋼軌型面匹配時的輪軌接觸點分布情況見圖3，車輪名義滾動圓和軌頂中心均位于橫坐標的零點處。由圖3可知，相同軌底坡時不同輪軌型面匹配的輪軌接觸點對分布存在明顯差異，相同輪軌型面匹配在不同軌底坡下的輪軌接觸點對也存在明顯差異，增加了地鐵車輪型面選擇和軌底坡設計的困難性。2種軌底坡下LM型面的接觸點對分布都比較均勻，接觸范圍較廣，使輪軌型面產生均勻且分布較廣的磨耗。S1002和DIN5573型面的接觸點均存在明顯的跳躍現象，在1/20軌底坡時接觸點過分集中。從接觸點對分布角度，S1002和DIN5773型面在輪對內側距為1 353 mm的條件下不適用于軌底坡為1/20的線路。篇幅所限，其他軌底坡下的輪軌接觸點對不一一列出。

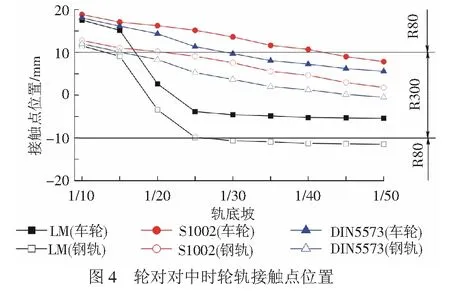
輪對對中時3種車輪型面在不同軌底坡下的輪軌接觸點位置見圖4。圖4中，車輪名義滾動圓和鋼軌的軌頂中心均位于縱坐標的零點處，鋼軌接觸點位置正、負分別表示接觸點位于軌頂外側、內側；車輪接觸點位置正、負分別表示接觸點位于車輪名義滾動圓外側、內側。對于LM型面，軌底坡為1/20時輪軌接觸點均位于踏面的中心附近；隨著軌底坡減小，鋼軌接觸點向內軌距角移動，軌底坡小于1/25后車輪與鋼軌R80圓弧接觸。S1002和DIN5573型面輪軌接觸點隨軌底坡的變化規律一致，隨著軌底坡減小，輪軌接觸點均向踏面中心移動，軌底坡小于1/20后車輪與軌頂R300圓弧接觸。

2.2 滾動圓半徑差和接觸角

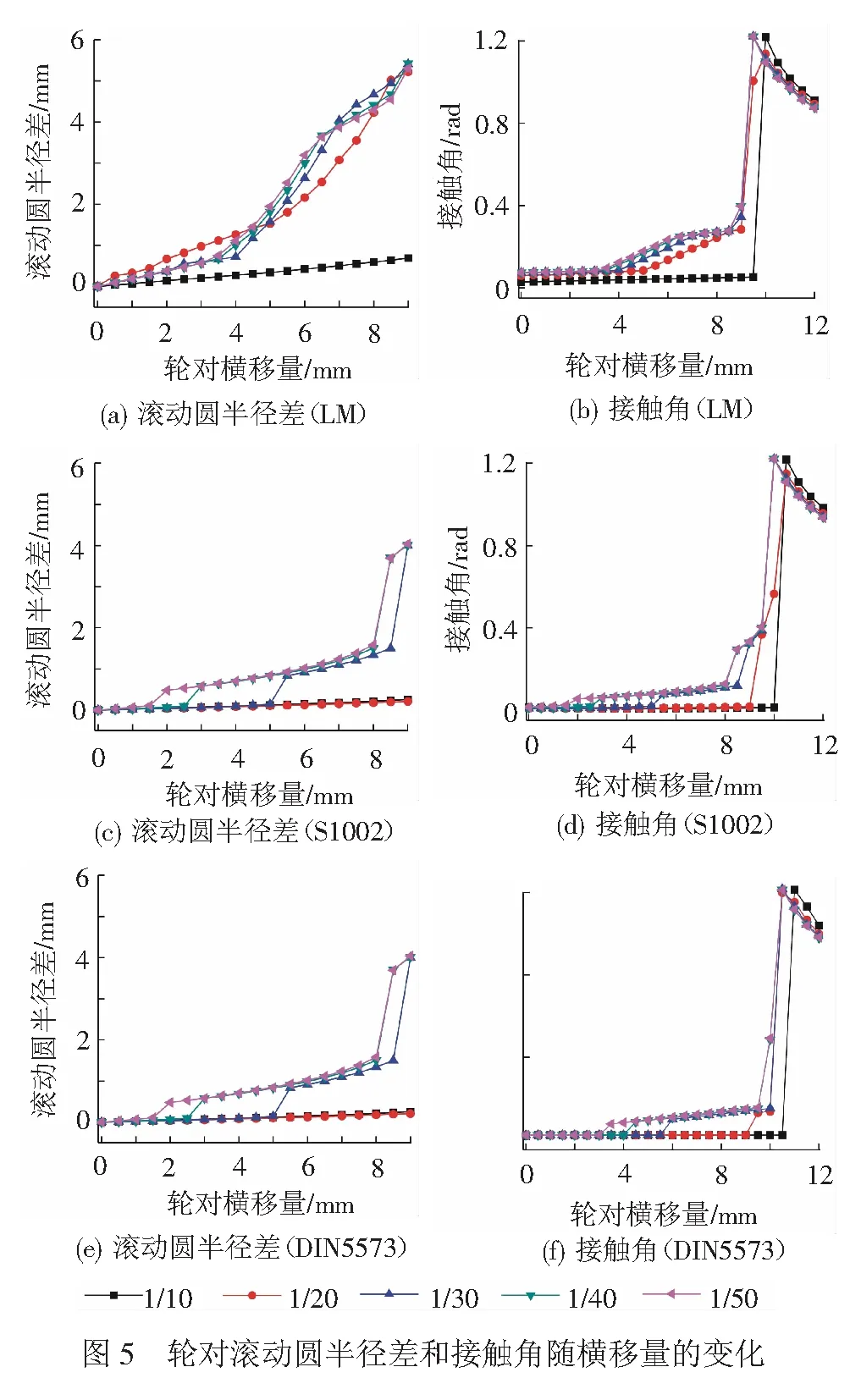
3種型面在不同軌底坡匹配情況下輪對滾動圓半徑差和接觸角隨橫移量的變化見圖5。對于LM型面，橫移量小于4 mm時不同軌底坡下滾動圓半徑差相差較小，1/20軌底坡下的滾動圓半徑差在1.26 mm以內，略大于其他軌底坡的值；橫移量大于4 mm后滾動圓半徑差迅速增大，軌底坡越小滾動圓半徑差越大。因此，在小半徑曲線段采用較小的軌底坡更有利于車輛的曲線通過。對于S1002和DIN5573型面，二者滾動圓半徑差變化趨勢一致，軌底坡大于等于1/20時，在發生輪緣貼靠前輪對的滾動圓半徑差均較小，軌底坡小于1/30時軌底坡對滾動圓半徑差的影響較小。相同軌底坡和橫移量時LM型面的滾動圓半徑差大于S1002和DIN5573型面。接觸角隨輪對橫移量和軌底坡的變化規律與滾動圓半徑差的變化規律基本一致。

2.3 縱向蠕滑率和自旋蠕滑率

3種型面不同軌底坡下的縱向蠕滑率和自旋蠕滑率隨輪對橫移量的變化見圖6，均為左側輪軌接觸的計算結果。

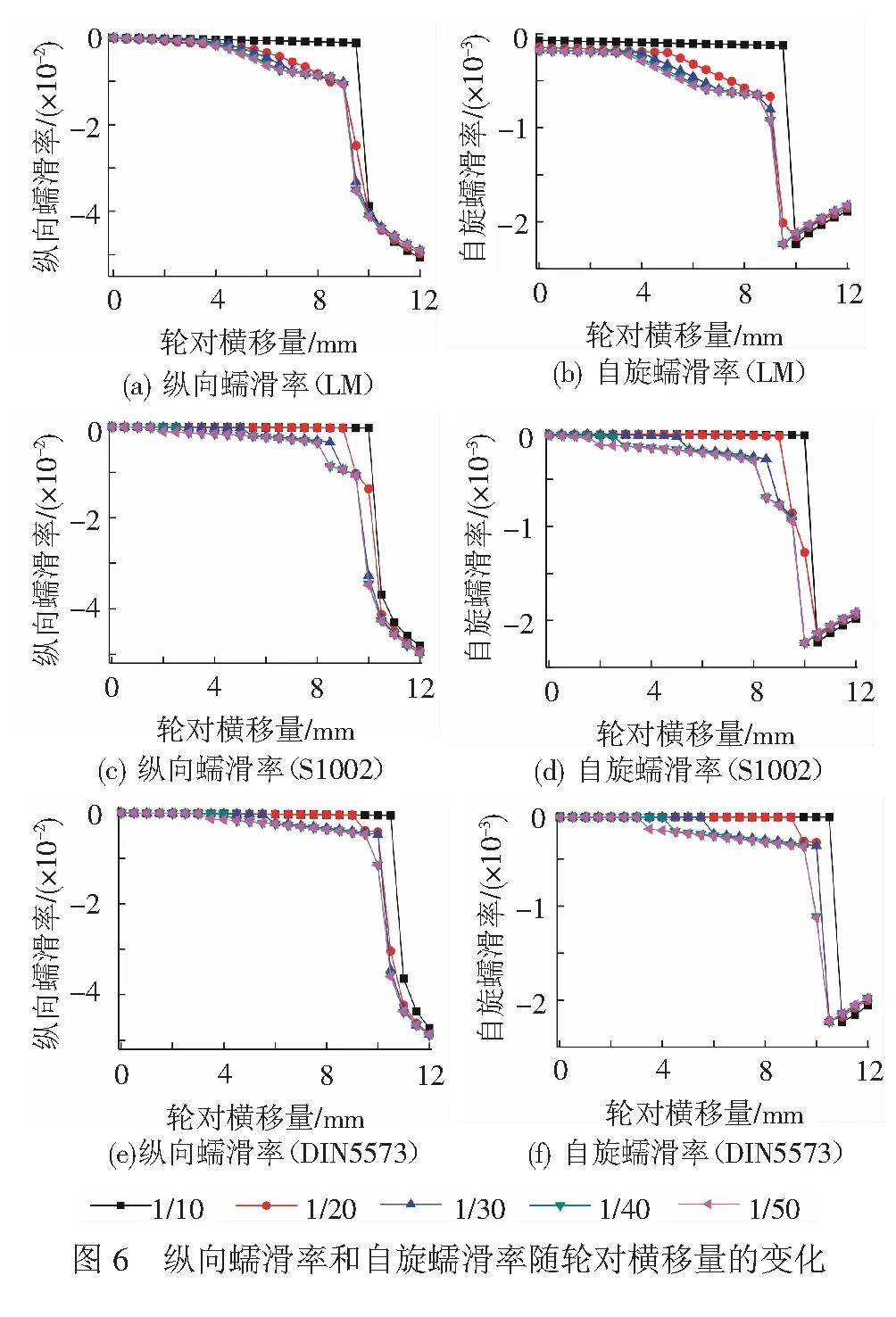
由式( 1 )可知，縱向蠕滑率主要受瞬時滾動圓半徑的影響。對于LM型面，輪對向左側橫移時，左輪瞬時滾動圓半徑隨輪對橫移量的增大而增大，導致左輪縱向蠕滑率的絕對值隨之增大；在輪緣貼靠時，縱向蠕滑率急劇增長，導致輪緣和鋼軌的側磨加劇。輪對橫移量較小時，由于不同軌底坡下瞬時滾動圓半徑相差不大，軌底坡對縱向蠕滑率的影響較小；橫移量大于4 mm時，相同輪對橫移量下瞬時滾動圓半徑隨軌底坡的減小而增大，導致縱向蠕滑率的絕對值隨之增大。S1002和DIN5573型面縱向蠕滑率相差較小，其絕對值小于LM型面，軌底坡小于1/30時軌底坡對縱向蠕滑率的影響較小。

由于計算中沒有考慮輪對搖頭速度的影響，自旋蠕滑率主要受接觸角的影響，見式(1)。自旋蠕滑率的絕對值隨軌底坡和輪對橫移量的變化規律與接觸角的變化規律一致。

3 軌底坡對輪軌接觸力學特性的影響

輪軌接觸特性的計算參數：軸重為14 t，輪軌材料的切變彈性模量82 GPa，泊松比為0.28，動、靜摩擦系數分別為0.29、0.3。本文計算中輪對向左側橫移，左側輪軌受力要大于右側，因此本節的輪軌蠕滑和接觸壓力等值均為左側輪軌接觸的計算結果。

3.1 蠕滑力

輪軌蠕滑力是引起輪軌磨耗和接觸疲勞損傷的主要原因。3種型面不同軌底坡下的縱向和橫向蠕滑力隨輪對橫移量的變化見圖7。從圖7可以看出，3種型面的縱向和橫向蠕滑力均隨輪對橫移量的增大呈先增大后減小的變化趨勢，主要是由于蠕滑力受到庫倫極限摩擦力的限制，摩擦力達到飽和時就不再增加，蠕滑率的增長不受限制，輪軌蠕滑率和蠕滑力之間表現出明顯的非線性特征。

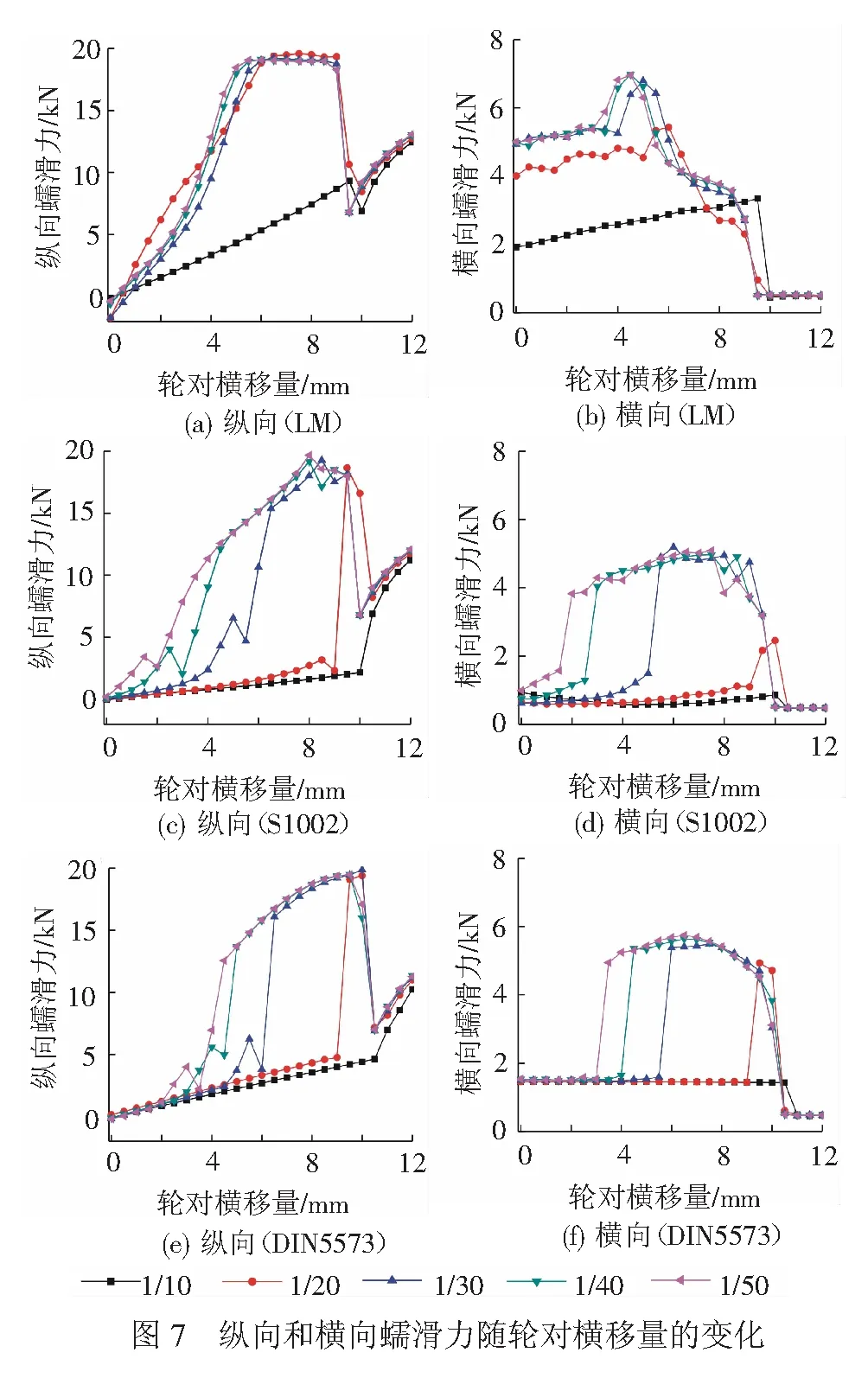
對于LM型面，輪對橫移量小于4 mm時1/20軌底坡下的縱向蠕滑力略大于其他軌底坡下的值，橫移量大于4 mm后基本表現為軌底坡越小縱向蠕滑力越大；橫向蠕滑力沒有表現出與縱向蠕滑率一致的規律。S1002和DIN5573型面縱向和橫向蠕滑力基本表現為隨軌底坡的減小而增大，但變化幅值較小。

3.2 接觸斑面積和接觸壓力

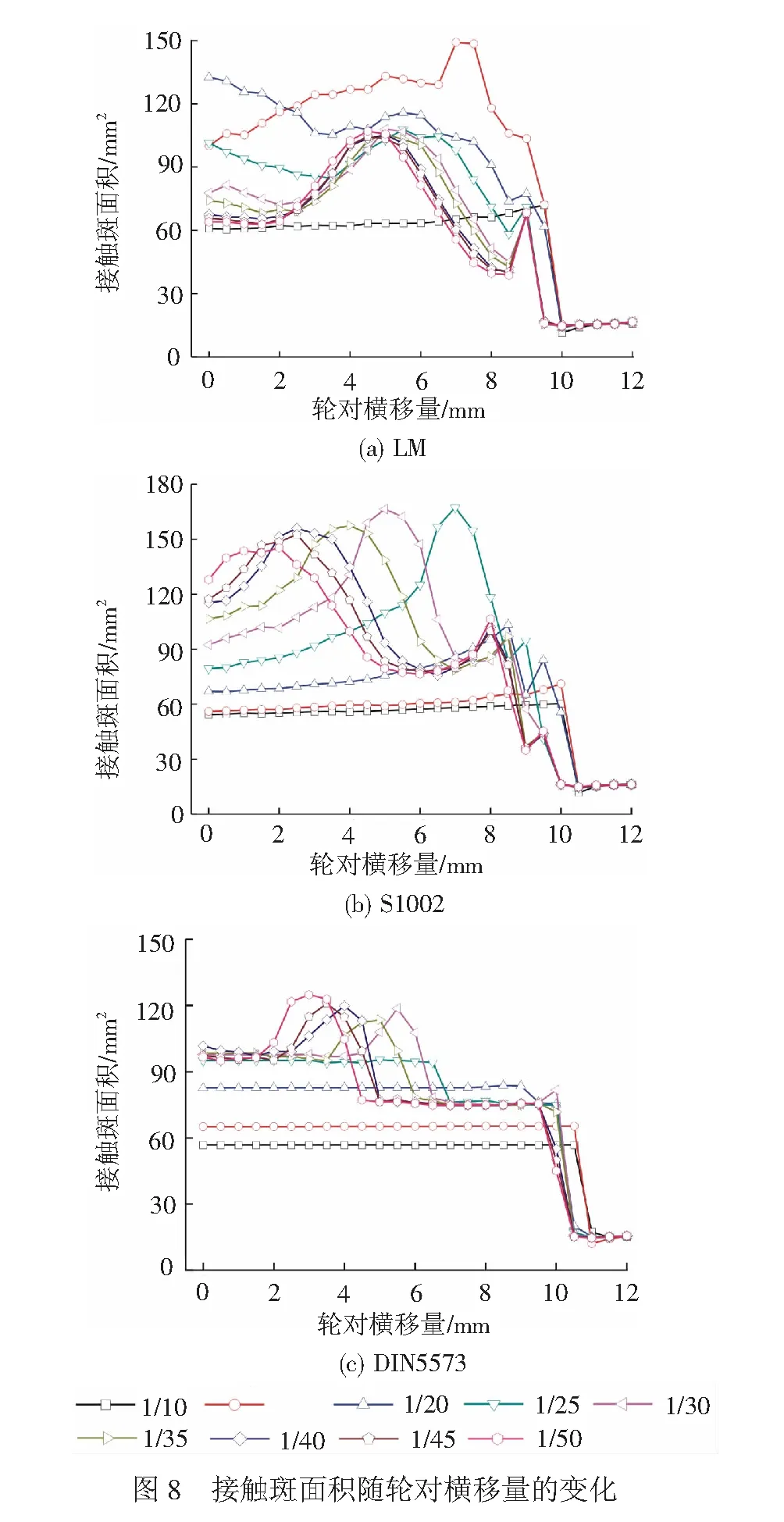
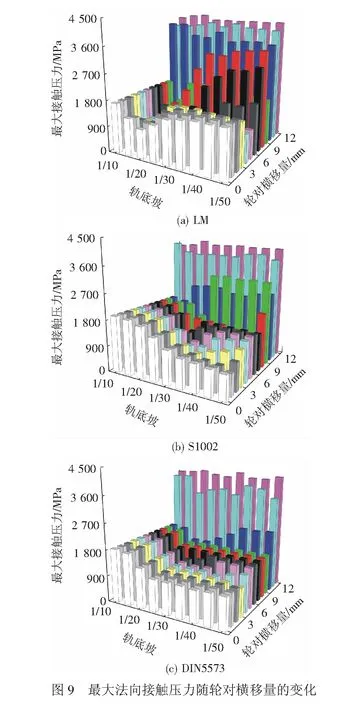
3種型面不同軌底坡下的接觸斑面積隨輪對橫移量的變化見圖8。對于LM型面，軌底坡小于1/25后，接觸斑面積隨輪對橫移量的變化規律一致，先略微減小，再增加，后又減小，軌底坡為1/30～1/50時接觸斑面積相差較小；軌底坡為1/15和1/20時，在輪緣根部接觸前接觸斑面積均較大，且大于90 mm2。對于S1002型面，軌底坡大于1/20時，接觸斑面積隨輪對橫移量變化較小，在輪緣貼靠后接觸斑面積急劇下降； S1002型面在其滾動圓附近采用了數值化設計理念，即采用了2條高次曲線代替圓弧，當車輪踏面中心附近與軌頂R300圓弧相接觸時輪軌接觸更加密貼，接觸點法向間隙非常小，輪軌型面匹配較好，軌底坡小于1/20時，隨著輪對橫移量的增加輪軌接觸點由名義滾動圓外側向踏面中心移動，然后再移向輪緣區域，導致輪軌接觸斑面積呈先增大后減小的變化趨勢，在輪緣貼靠鋼軌后接觸斑面積急劇減小。對于DIN5573型面，軌底坡大于等于1/20時，在輪緣貼靠前車輪上接觸點均位于踏面1∶46的直線段，導致輪軌接觸斑面積幾乎不隨輪對橫移量的變化而變化；軌底坡小于1/25時，在輪緣貼靠前接觸斑面積隨輪對橫移量的變化出現了2個平臺，接觸斑面積的變化相對較小。

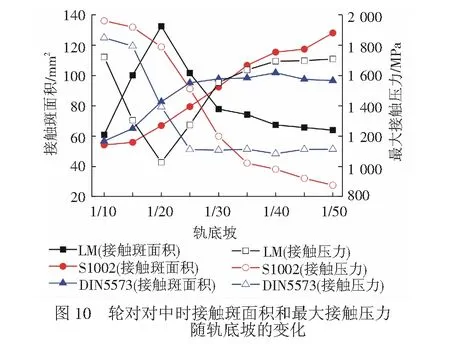
3種型面輪對對中位置時的接觸斑面積和最大法向接觸壓力隨軌底坡的變化曲線見圖10。從圖10可以看出，LM型面接觸斑面積隨軌底坡的減小呈先增大后減小的變化趨勢，最大法向接觸壓力隨軌底坡的變化規律剛好與接觸斑面積的變化規律相反。軌底坡為1/20時接觸斑面積和最大法向接觸壓力分別為132.6 mm2和1 027 MPa，軌底坡為1/40時分別為67.5 mm2和1 694 MPa，1/20軌底坡時接觸斑面積比1/40軌底坡約大1倍，最大接觸壓力約小39.4%。S1002型面接觸斑面積隨軌底坡的減小而增大，最大法向接觸壓力隨軌底坡的減小而減小。DIN5573型面接觸斑面積隨軌底坡的減小先增大，軌底坡小于等于1/25時接觸斑面積變化較小，約100 mm2，最大接觸壓力在軌底坡小于等于1/25時約為1 100 MPa。

3.3 接觸應力

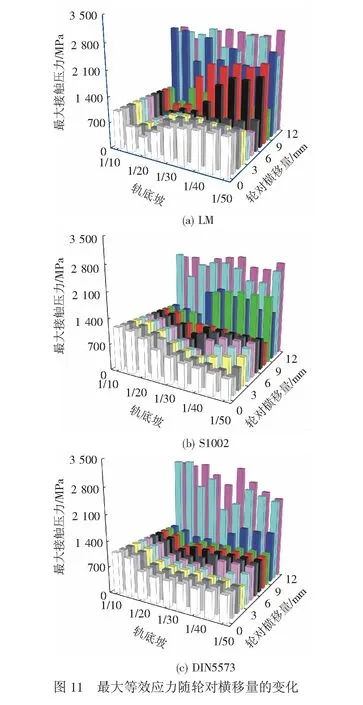
3種型面不同軌底坡下的最大等效應力隨輪對橫移量的變化見圖11。最大等效應力隨隨軌底坡和輪對橫移量的變化規律與最大法向接觸壓力的變化規律一致，最大剪切應力的變化規律又與等效應力的變化規律一致，在此不再贅述。

3種型面輪對對中位置時的最大等效應力和最大剪切應力隨軌底坡的變化曲線見圖12。從圖12可以看出，軌底坡對LM型面的最大等效應力和最大剪切應力的影響較大，軌底坡為1/20時最大等效應力和最大剪切應力分別為498 、259 MPa，軌底坡為1/40時分別為1 014、543 MPa，1/40軌底坡時最大等效應力和剪切應力比1/20軌底坡時約大1倍。顯然，LM型面采用1/20軌底坡能大大降低輪軌接觸應力，提高輪軌的使用壽命。S1002型面最大等效應力和最大剪切應力隨軌底坡的減小而增大，采用較小軌底坡對輪軌的使用壽命更有利。對于DIN5573型面，軌底坡小于等于1/25后軌底坡對最大等效應力和最大剪切應力的影響較小，分別約為700、350 MPa。

4 結論

本文從輪軌接觸幾何關系和輪軌非赫茲滾動接觸理論兩方面分析比較了我國現采用的3種地鐵車輪型面LM、S1002和DIN5573與CHN60鋼軌在不同軌底坡下的匹配關系，從靜力學分析角度尋找最優軌底坡匹配。研究結果表明：

(1) 1/20軌底坡下LM型面最大接觸壓力、等效應力和剪切應力等參數遠小于現行的1/40軌底坡，輪對橫移量大于5 mm后1/40軌底坡下的滾動圓半徑差明顯大于1/20軌底坡。LM型面直線段最優軌底坡為1/20，曲線段采用1/40軌底坡有利于車輛的曲線通過，降低輪軌磨耗。

(2) S1002型面最大接觸壓力、等效應力和剪切應力等參數隨軌底坡的減小而減小，軌底坡為1/40時輪軌型面匹配較優。

(3) DIN5573型面在軌底坡小于1/25時軌底坡對輪軌接觸特性的影響較小，軌底坡在1/40～1/30范圍內輪軌型面匹配較優。

參考文獻：

培育壯大新動能有利于應對新技術革命。新一輪全球技術革命主要表現為信息技術革命、智能技術革命、新能源技術革命等方面。培育壯大新動能，既可為應對新技術革命培育新企業等創新型主體，又可為應對新技術革命提供新技術等新要素支撐，更可為應對新技術革命提供新制度、新市場等環境。

[1] 曾向榮, 李文英, 高曉新. 城市軌道交通工程鋼軌軌底坡取值的探討[J]. 都市快軌交通, 2006, 19(6): 57-60.

ZENG Xiang-rong, LI Wen-ying, GAO Xiao-xin. On the Rail Base Inclination in Urban Rail Transit Project[J]. Unban Rapid Rail Transit, 2006, 19(6): 57-60.

[2] 中華人民共和國建設部.GB 50157—2003 地鐵設計規范[S]. 北京: 中國計劃出版社, 2003.

[3] 曾向榮, 吳建忠, 孫大新, 等. 首都機場線直線電機系統的軌道設計與創新[J]. 都市快軌交通, 2009, 22(1): 62-66.

ZENG Xiang-rong, WU Jian-zhong, SUN Da-xin, et al. Innovative Track Design for the Linear Motor System on Capital Airport Express[J]. Unban Rapid Rail Transit, 2009, 22(1): 62-66.

[4] 沈鋼, 張定賢. 軌底坡對曲線鋼軌側磨影響的研究[J]. 鐵道學報, 1994, 16(3): 94-99.

SHEN Gang, ZHANG Ding-xian. Research on Readjusting Rail Inclinations for Reducing Rail Side-cutting[J]. Journal of the China Railway Society, 1994, 16(3): 94-99.

[5] 周亮. 上海地鐵曲線軌道減磨措施試驗研究[J]. 城市軌道交通研究, 2009,(9): 62-66.

ZHOU Liang. Test And Research about the Measures of Alleviating Rail Wear in Shanghai Metro[J]. Urban Mass Transit Information, 2009,(9): 62-66.

[6] 鄧建輝, 陳朝陽, 鄧勇, 等. 軌底坡和軌頭廓面對鋼軌接觸疲勞損傷的影響研究[J]. 鐵道建筑, 2011, (8): 109-111.

DENG Jian-hui, CHEN Zhao-yang, DENG Yong, et al. Research on the Effect of Rail Cant and Rail Profiles on Contact Fatigue Damage of Rail[J]. Railway Engineering, 2011,(8): 109-111.

[7] 陶功權. KKD客車車輪踏面剝離成因初探[D]. 成都: 西南交通大學, 2013: 69-71.

[8] 李霞, 溫澤峰, 金學松. 鋼軌軌底坡對LM和LMA兩種輪對接觸行為的影響[J]. 機械工程學報, 2008, 44(3): 64-69.

LI Xia, WEN Ze-feng, JIN Xue-song. Effect of Rail Cant on Rolling Contact Behavior of LM and LMAWheelsets[J]. Chinese Journal of Mechanical Engineering, 2008, 44(3): 64-69.

[9] 李霞, 溫澤峰, 張劍, 等. 軌底坡對輪軌滾動接觸行為的影響[J]. 機械強度, 2009, 31(3): 475-480.

LI Xia, WEN Ze-feng, ZHANG Jian, et al. Effect of Rail Cant on Wheel/Rail rolling Contact Behavior[J]. Journal of Mechanical Strength, 2009, 31(3): 475-480.

[10] 張劍, 宋慧玲, 王生武, 等. 地鐵車輛輪軌型面匹配分析[J]. 大連交通大學學報, 2012, 33(5): 1-6.

ZHANG Jian, SONG Hui-ling, WANG Sheng-wu, et al. Analysis of Matching Relationship of Metro Vehicle Wheel and Rail Profiles[J]. Journal of Dalian Jiaotong University, 2012, 33(5): 1-6.

[11] ZAKERI, J A, FATHALI M, ROUDSARI N B. Effects of Rail Cant on Wheel-Rail Contact Forces in Slab[J]. International Journal of Mechanics and Applications, 2011, 1(1): 12-21.

[12] SADEGHI J, FATHALI M, BOLOUKIAN N. Development of a New Track Geometry Assessment Technique Incorporating Rail Cant Factor[J]. Proceedings of the Institution of Mechanical Engineers Part F:Journal of Rail and Rapid Transit, 2009, 223(3): 255-263.

[13] 范鐵華, 馬敬波, 羅清士, 等. 小半徑曲線鋼軌非正常側磨分析及防治措施[J]. 鐵道學報, 1990, 12(3): 39-46.

FAN Tie-hua, MA Jing-bo, LUO Qing-shi, et al. Analysis of Excessive Rail Side-wear on Small-radius Curves and its Prevention[J]. Journal of the China Railway Society, 1990, 12(3): 39-46.

[14] 王開文.車輪接觸點跡線及輪軌接觸幾何參數的計算[J]. 西南交通大學學報,1984,18(1):89-99.

WANG Kai-wen. The Track of Wheel Contact Points and the Calculation of Wheel/rail Geometric Contact Parameters[J]. Journal of Southwest Jiaotong University, 1984,18(1):89-99.

[15] 金學松, 劉啟躍. 輪軌摩擦學[M]. 北京: 中國鐵道出版社, 2004.

[16] KALKER J J. Three-dimensional Elastic Bodies in Rolling Contact[M]. Dordrecht: Kluwer Academic Publishers, 1990.

[17] POLACH O. Wheel Profile Design for Target Conicity and Wide Tread Wear Spreading[J]. Wear, 2011, 271(1): 195-202.