關聯規則挖掘在電子對抗目標分析中的應用

李 政，祝 利，韋 偉

（電子工程學院，合肥 230037）

0 引 言

信息化戰場上的電子對抗目標之間、電子對抗目標與其它武器系統、作戰行動之間往往是相互聯系的。掌握這種關聯關系，可以更加準確地把握電子對抗目標的活動規律，并對其活動進行預測，為電子對抗作戰和其它作戰預案的制定提供依據。

對于電子對抗目標的關聯分析，目前主要基于先驗知識的人工判斷。隨著電子對抗目標增多及其活動規律日益復雜，上述方法愈加難以實現。如何從海量偵察數據中使用自動化方法對電子對抗目標進行關聯分析，成為一個亟待解決的問題。

1 關聯規則挖掘

關聯規則挖掘是數據挖掘的一個重要領域，是模式挖掘的一種基本形式，其目的是挖掘和搜索數據集中反復出現的聯系。關聯規則有些是常識、經驗性的，而另一些則是啟發性的。

隨著可分析數據量的增大，關聯規則挖掘越來越受到重視。例如在商業領域，從大量交易數據中發現相關聯系，可以為產品促銷、超市貨架規劃、顧客購買習慣分析提供決策支持。

1.1 相關概念

1.1.1 關聯規則

設I＝｛i1，i2，…，im｝為項集，D是數據庫事務的集合，其中每個事務T是一個非空項集且T?I。設A是一個項集，包含于事務T中。關聯規則形如A?B，其中A?I，B?I，A≠?，B≠?，并且A∩B≠?［1］。關聯規則表示某一類或幾類項目與另一類項目之間存在的單向影響關系。關聯規則的典型案例是購物籃模型，例如通過對顧客購物籃內貨物的分析，可以發現牛奶和面包等某幾種貨物總是頻繁地一起出現。這個例子中，“購買牛奶的顧客更傾向于買面包”即是一條關聯規則，可以表示為：

1.1.2 支持度與置信度

支持度s表示A∪B在事務D中所占的百分比，即s（A?B）＝P（A∪B）。置信度c表示D包含A的事務的同時包含B的事務的百分比，即c（A?B）＝P（B｜A）。支持度和置信度是對于規則的2種度量，分別表示規則的普適程度和確定程度。最終挖掘的結果與挖掘算法中最小支持度與置信度閾值的取值有很大關系，若取值過高，難以發現關聯規則，若取值較低，關聯規則的參考價值就會大打折扣，且其數目會過多。在上述“牛奶與面包”的例子中，若關聯規則的支持度為5%，置信度為60%，可以表示為：

1.1.3 頻繁項集

若項集I滿足設定的最小支持度閾值，則稱I為頻繁項集。上述例子中，由于牛奶和面包總是頻繁地一起出現在購物籃中，若其滿足相應的支持度與置信度條件，則＜牛奶，面包＞構成了一個頻繁項集。根據支持度與置信度的定義，置信度與支持度有如下關系：

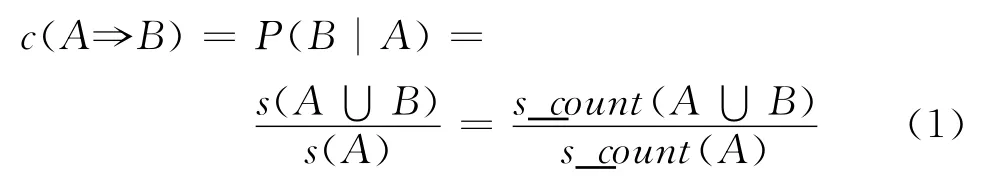
式中：s＿count（）為支持度計數。

根據式（1），A?B的支持度與置信度很容易從A、B和A∪B的支持度計數中得出，也就是說一旦確定A、B和A∪B的支持度計數s＿count（A）、s＿count（B）和s＿count（A∪B），就能確定關聯規則A?B或B?A。因此，關聯規則的挖掘可以最終歸結為確定頻繁項集。

1.2 典型算法

關聯規則挖掘一般可以分為2個步驟：第一是找出所有的頻繁項集，第二是由頻繁項集確定關聯規則。典型的關聯規則挖掘算法基本上按照上述步驟進行挖掘。

1.2.1 Apriori算法

Apriori算法于1994年由Agrawal和R.Srikant提出，是一種多候選產生類布爾型關聯規則挖掘算法。由于該算法采用逐層搜索的迭代方法，每次找出一組頻繁項集就要對數據進行一次掃描，為了減少計算量，采用“頻繁項集的所有非空子集也是頻繁項集”這一先驗性質壓縮掃描空間［2］。

1.2.2 FP－growth算法

由于Apriori算法需要產生大量的候選集以便從中尋找頻繁項集，并需要重復多次掃描數據庫，影響了算法的效率。針對這些問題，Jiawei Han于2000年提出頻繁模式增長（FP－growth）算法。該算法首先將數據集構建成1棵頻繁模式樹（FP－tree），再基于頻繁模式樹對頻繁項集進行挖掘。該算法僅需對數據集進行2次完整的掃描，且可以明顯地壓縮所要搜素的數據集的大小，因此得到了廣泛應用。1.2.3 序列規則挖掘算法

序列規則是在普通關聯規則基礎上添加時間信息，對于每一個時間段，都有在該時間段收集到的數據與之對應，即有多少時間段就有多少數據集［3］。在序列規則挖掘中，時間段代替了普通關聯規則挖掘中的“購物籃”。典型的序列規則挖掘算法有基于FP－tree的高效數據流頻繁項集挖掘算法FPStream和針對滑動時間窗口的FTP－DS頻繁項集挖掘算法等［4］。

2 基于關聯規則的電子對抗目標關聯分析

戰場上，電子對抗目標之間、電子對抗目標與武器系統及作戰行動之間的關聯關系表現為2種模式：

一是電子對抗目標、武器系統、其它作戰力量同時活動，體現出協同關系，例如多部雷達同時對同一目標進行探測；

二是電子對抗目標、武器系統、作戰力量依次活動，體現出時序關系。例如防空導彈對敵機進行攔截時，預警探測雷達往往先于制導火控雷達工作。

對于這2種模式，分別對其采用靜態關聯規則挖掘算法和序列規則挖掘算法進行分析。

2.1 靜態關聯規則挖掘

針對電子對抗目標、武器系統、作戰力量同時活動的情況，采用包含時間信息的FP－growth算法對其中的關聯規則進行挖掘。挖掘過程主要有以下步驟：

（1）數據處理

常規的FP－growth算法的數據中并沒有時間信息，為了體現目標同時出現的情況，將常規算法中的事務T設為時間段，即用時間段代替“購物籃”，將時間段盡量設小，以體現目標出現的同時性。

電子對抗偵察數據中重要的參數是目標的出現和消失時間，對其進行關聯規則挖掘時只需關注目標編號和目標活動時間這2個參數。在此將偵察數據整理成表1所示的形式，即每個時間段及在該時間段內出現的目標編號。

表1的時間段設定成1 s。需要注意的是，目標編號處不僅可以是電子對抗目標，也可以是其他武器系統或作戰行動。

（2）確定初始頻繁項集

對數據集進行完整掃描，對目標Ii出現的次數計數，確定支持度計數不小于最小支持度閾值的目標集合L，并按支持度計數遞減排序。這里舉例設：

表1 數據格式

（3）構造FP－tree

首先創造樹的根節點，記為n。對數據集進行掃描，創建樹的分枝。例如t1時間段包含I1、I2、I53項，其在L中的次序是I2、I1、I5。將I2作為根節點的子節點鏈接到n，I1鏈接到I2，I5鏈接到I1。t1時間段包含I2、I4項，其中I2鏈接到n，I4鏈接到I2。由于之前已經創建節點I2，因此I4與t1時間段共享節點I2。依此法構造FP－tree（如圖1所示），就可將頻繁項集挖掘問題轉化為FP－tree挖掘問題。

圖1 FP－tree

（4）挖掘頻繁項集

FP－tree的挖掘過程如下：首先由長度為1的頻繁模式（初始后綴模式）開始，構造其條件模式基，然后構造其FP－tree并對其進行遞歸挖掘。

以上面構建的FP－tree為例，首先考慮I5，I5出現在2個分支中，分別為路徑 〈I2，I1，I5：1〉和〈I2，I1，I3，I5：1〉。以I5為后綴，其前綴路徑為 〈I2，I1：1〉和〈I2，I1，I3：1〉構成I5的條件模式基。使用上述條件模式基構建 FP－tree，該樹僅具有 〈I2：2，I1：2〉1個分支，因為I3的支持度計數不滿足最小支持度閾值。因此，該路徑包含的頻繁模式為依此法對其它目標進行頻繁項集挖掘，即可確定所有項集模式。

（5）確定關聯規則

挖掘出所有頻繁項集后，可以直接由其產生滿足最小支持度和置信度的強關聯規則：

首先，對于每個頻繁項集l產生其所有非空子集m。

其次，對于非空子集m，如果tmin＿c，則 產 生 關 聯 規 則m?（l－m）。 其 中s＿count（）為支持度計數，tmin＿c為最小置信度閾值。

（6）評估關聯規則

由于置信度有時不能完全反應A、B相關性的實際強度，尤其是支持度閾值較低或關聯規則較長時。因此必須采用其它指標對關聯規則進行評估，在這里選用提升度指標：

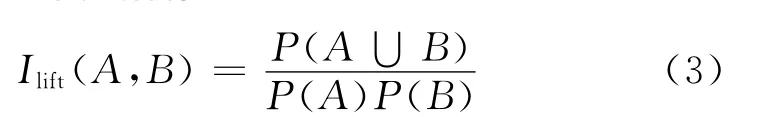
若提升度小于1，表示A、B是負相關，而提升度大于1則表示A、B正相關。對前面挖掘出的關聯規則使用提升度進行評估后，即可得到最終有價值的關聯關系。

2.2 序列關聯規則挖掘

序列挖掘是對相對次序或時間出現頻率高的模式進行發現的方法。上述對于電子對抗目標的靜態關聯規則挖掘雖然數據集包含時間信息，但在挖掘中沒有體現，挖掘的內容是電子對抗目標、武器系統、作戰單位同時活動時的關聯規則。序列關聯規則挖掘在上述方法的基礎上加上了時間因素，能夠反映電子對抗目標、武器系統、作戰單位依次活動時的規律。

序列挖掘采用和關聯規則挖掘類似的過濾算法，所需的數據格式與靜態關聯規則挖掘算法相同，可采用R語言和Statistica等軟件進行實現。除支持度、置信度、提升度等指標外，進行關聯模式挖掘需要注意的還有最大間隔指標，該指標表示關聯規則中2個目標出現時間的最大間隔［5］。該值若設置過大，則難以體現目標的關聯性。

3 關聯規則挖掘仿真與分析

3.1 基于FP－growth的靜態關聯規則挖掘的仿真

下面以2 220條模擬偵察數據進行仿真。該批數據中共有A、B、C、D、E5個電子對抗目標，時間以1 s為1段，共計2 220 s，分別以支持度5%、10%、15%、20%，置信度60%進行挖掘，仿真發現支持度為10%時可以獲得一定數目有價值的關聯規則，剔除關聯規則中提升度不大于1的數據，得到關聯規則如表2所示。

表2 部分挖掘的關聯規則

從表格中可見，目標B、C關聯性較強，目標C出現時B出現的頻率以及B出現時C出現的支持度都達到了65%以上。另外，目標A、B出現時目標C出現的次數雖然不多，但置信度和提升度最高，可見該規則具有很高的參考價值，在偵察活動中若發現A、B目標同時活動，應重點關注C目標。將目標活動情況進行可視化顯示（如圖2所示），從中可以發現B、C目標活動規律的關聯性十分明顯，但是對于其它關聯的活動規律難以通過人工判斷進行挖掘，而采用FP－growth靜態關聯規則挖掘算法就能很好地對其進行分析，體現出該方法的有效性。

圖2 目標活動規律

3.2 序列關聯規則挖掘的仿真

仿真時使用R語言arulesSequences程序包對一批模擬偵察數據進行挖掘，數據集中有A、B、C、D、E、F、G、H共8個電子對抗目標，每個時間段劃分為1 min，支持度分別設為5%、10%、15%、20%，置信度為60%，最大時間間隔為10 min，仿真發現支持度為20%時可以獲得一定數目有價值的關聯規則，如表3所示。

表3 部分挖掘的關聯規則

從表中結果可見，目標F在目標A之后10 min之內出現的支持度達到了45%，在偵察中若發現目標A活動，應及時在目標B的頻段對其進行控守。序列｛B，F｝、｛A，B｝支持度也較高，值得關注。

4 結束語

本文針對電子對抗目標之間、電子對抗目標與武器系統及作戰行動之間的2種關聯模式，分別采用了包含時間信息的FP－growth靜態關聯規則挖掘算法和序列關聯規則挖掘算法進行挖掘。仿真結果表明，通過上述方法可以揭示電子對抗目標之間、電子對抗目標與武器系統及作戰行動之間同時活動和依次活動2種關聯關系，能夠為電子對抗及其它作戰行動提供決策參考，具有一定的實用價值。

［1］Jiawei Han.Data Mining Concept and Techniques［M］.北京：機械工業出版社，2012.

［2］Rakesh Agrawal，Ramakrishnan Srikant.Mining sequential patterns［A］.Proceedings of The Eleventh International Conference on Data Engineering［C］.Washington D C，USA：IEEE Computer Society，1995：3－14.

［3］王星.大數據分析：方法與應用［M］.北京：清華大學出版社，2013.

［4］馬青霞，李廣水，孫梅.頻繁模式挖掘進展及典型應用［J］.計算機工程與應用，2011，47（15）：138－142.

［5］閆明月，侯忠生，高穎.一種面向布爾時間序列的關聯規則挖掘算法［J］.控制與決策，2012（10）：1147－1151.