電液伺服系統(tǒng)非線性振動誘因探究

， 　， ， (1.燕山大學(xué) 河北省重型機械流體動力傳輸與控制重點實驗室， 河北 秦皇島　066004；2.燕山大學(xué) 先進鍛壓成形技術(shù)與科學(xué)教育部重點實驗室， 河北 秦皇島　066004)

引言

電液伺服系統(tǒng)是一個非線性動力學(xué)系統(tǒng)，其在運行過程中容易產(chǎn)生噪聲或出現(xiàn)沖擊、爬行和非線性振動等異常現(xiàn)象，而且誘因不易確定，影響系統(tǒng)的穩(wěn)定工作[1]。

目前，對電液伺服系統(tǒng)動態(tài)特性的研究一般采用系統(tǒng)建模和數(shù)值仿真手段[2,3]，所依據(jù)的理論多是經(jīng)典控制理論和線性動力學(xué)理論，較少運用非線性動力學(xué)理論進行分析研究。而且，多數(shù)在系統(tǒng)建模時對非線性因素進行線性化處理[4,5]，研究結(jié)論與實際情況有較大差異，很難解釋實際動態(tài)測試中出現(xiàn)的時域波形繁雜、周期振蕩等異常現(xiàn)象，不能準(zhǔn)確反映執(zhí)行機構(gòu)的運動特征。

本研究根據(jù)非線性動力學(xué)原理，重點探究彈簧力和摩擦力等非線性因素對電液伺服系統(tǒng)運動特征的影響規(guī)律。通過理論研究及仿真分析，揭示系統(tǒng)執(zhí)行機構(gòu)運動的非線性動力學(xué)本質(zhì)，旨在為揭示電液伺服系統(tǒng)非線性振動的誘因提供理論借鑒。

1　動力學(xué)模型

電液伺服系統(tǒng)的執(zhí)行機構(gòu)為伺服液壓缸，本研究以常用的雙作用單活塞桿液壓缸為例進行分析，其工作原理如圖1所示。

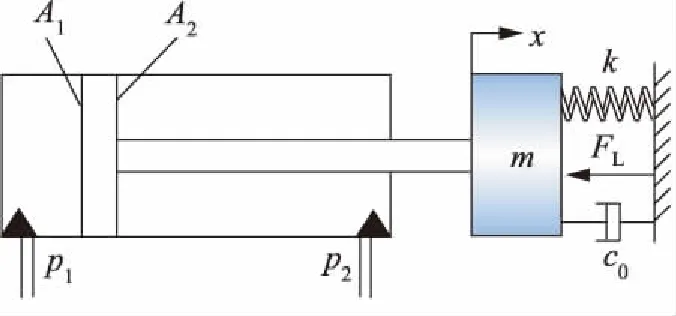
圖1　液壓缸工作原理

其動力學(xué)方程為：

(1)

式中，m為活塞及負載的折合質(zhì)量；x為活塞位移；Fc為黏性力；Fs為彈性力；Ff為摩擦力；FL為負載力；p1、p2分別為無桿腔和有桿腔壓力；A1、A2分別為無桿腔和有桿腔活塞有效作用面積。

2　非線性作用力及作用特征

2.1　非線性彈簧力及作用特征

液壓缸系統(tǒng)彈簧剛度由活塞桿剛度和液壓油剛度串聯(lián)合成，彈簧力主要來自于受控液壓油所構(gòu)成的液體彈簧。活塞運動會改變兩側(cè)液體彈簧的長度，引起液壓彈簧剛度的改變，變化規(guī)律為[1]：

(2)

式中，βe為油液體積彈性模量；L為液壓缸總行程；L1為活塞初始位置，即無桿腔液柱長度；VL1、VL2分別為閥與無桿腔和有桿腔之間管道內(nèi)油液體積；α、γ為待定系數(shù)。

由式(2)可得出液壓彈簧剛度隨活塞位移的變化規(guī)律，如圖2所示。

由圖2可知，液壓彈簧剛度隨活塞的運動呈現(xiàn)出非線性時變規(guī)律。當(dāng)α>0、γ=0時呈現(xiàn)軟彈簧特性，α=0、γ>0時呈現(xiàn)硬彈簧特性，α>0、γ>0時呈現(xiàn)半程軟彈簧、半程硬彈簧特性[6]。

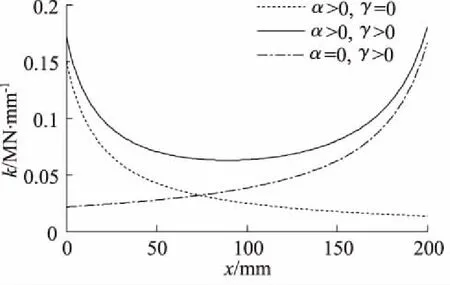
圖2　液壓彈簧剛度隨活塞位移的變化規(guī)律曲線

設(shè)y為在工作點x附近的振動位移，即Δx。將液壓彈簧剛度在工作點附近展成泰勒級數(shù)形式：

(3)

k(x+y)=k1+k2y+k3y2+o(y2)

(4)

此時，液壓缸系統(tǒng)的彈簧力可以表示為：

Fs=k(x+y)·y=k1y+k2y2+k3y3+o(y3)

(5)

另外，綜合考慮彈簧彈性勢能的對稱性以及其與彈簧力之間的關(guān)系，并去除高階無窮小項o(y3)，彈簧力可以進一步表達為[6]：

Fs≈k1y+k3y3

(6)

暫不考慮摩擦力的非線性因素，集中研究非線性彈簧力對系統(tǒng)運動特征的影響，系統(tǒng)動力學(xué)方程式(1)在工作點x附近的特性可表達為：

=p1A1-p2A2-FL-Ff(v)

=Fsin(ωt+φ0)

(7)

式中，c0為結(jié)構(gòu)阻尼系數(shù)，c1為線性摩擦系數(shù)。此外，因液壓缸中油壓有微觀波動，基本服從簡諧振動規(guī)律，故式(7)右邊可近似表示為Fsin(ωt+φ0)，是系統(tǒng)的激振源[7]。F為激振力振幅；ω為激振角頻率；φ0為激振力的初相。

由非線性動力學(xué)理論可知，式(7)是含有阻尼的Duffing方程。該方程為研究電液伺服系統(tǒng)的非線性彈簧力的作用特征提供了結(jié)構(gòu)模型。

進一步將式(7)化為式(8)的形式，并用“諧波平衡法”[8]進行求解，可得幅頻關(guān)系式(9)。

(8)

(9)

式中，A為零次近似解的振幅。

由幅頻關(guān)系式可得幅頻特性曲線，如圖3所示。當(dāng)β>0時為尾部右偏曲線；當(dāng)β<0時為尾部左偏曲線。阻尼的作用限制了共振振幅的無限上升。當(dāng)激勵頻率從小到大或從大到小變化時，會發(fā)生振幅突然變化的“跳躍現(xiàn)象”[1]。

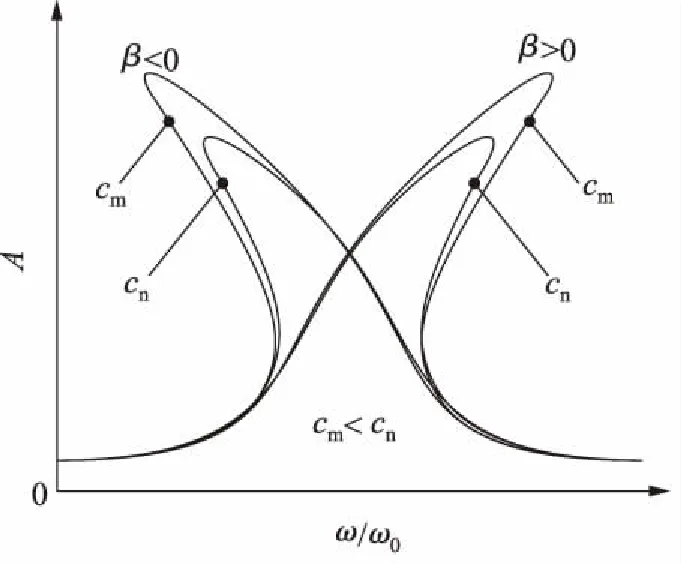
圖3　幅頻特性曲線

另外，Duffing方程在相平面上有三個平衡點，初始條件決定系統(tǒng)在不同流域中的軌線將趨于不同的穩(wěn)定定點。當(dāng)外加周期力不等于零時，系統(tǒng)便有可能在不同流域之間來回跳動，從而形成復(fù)雜的振蕩狀態(tài)，做各種復(fù)雜的運動[9]。

2.2　非線性摩擦力及作用特征

圖4所示為體現(xiàn)摩擦力與速度關(guān)系的Stribeck曲線[10]。

圖4　Stribeck曲線

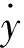
(10)

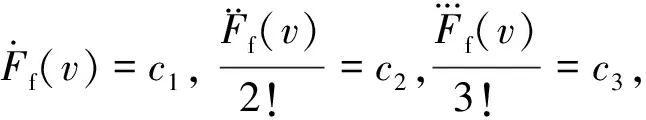
(11)

暫不考慮彈簧力的非線性因素，集中研究非線性摩擦力對系統(tǒng)運動特征的影響。摩擦力的作用效果隨工作點在Stribeck曲線上所處區(qū)段不同而異。當(dāng)工作點在區(qū)域II或III時，摩擦力呈現(xiàn)非線性時變特性。此時，在工作點附近，有[11]：

則系統(tǒng)動力學(xué)方程式(1)在工作點x附近的特性可表達為：

(12)

(13)

由非線性動力學(xué)理論可知，式(13)是受迫Van Der Pol方程。該方程為研究電液伺服系統(tǒng)的非線性摩擦力的作用特征提供了結(jié)構(gòu)模型。Van Der Pol方程存在極限環(huán)，如圖5所示[1]。當(dāng)|c1|>c0時，摩擦力作用的效果是產(chǎn)生極限環(huán)型振蕩[12]。

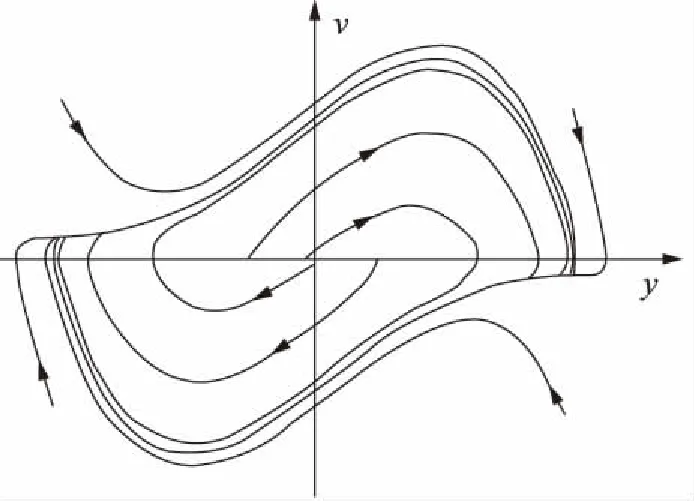
圖5　Van Der Pol 極限環(huán)

2.3　非線性彈簧力和非線性摩擦力耦合作用特征

由上述分析可知，非線性彈簧力的作用特征可以用Duffing方程描述；非線性摩擦力的作用特征可以用Van Der Pol方程描述。

進一步研究發(fā)現(xiàn)，同時考慮彈簧力和摩擦力的非線性作用，可得到如下形式的動力學(xué)方程：

(14)

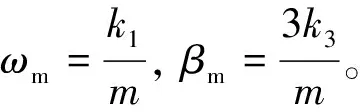
由非線性動力學(xué)理論可知，上式是Duffing-Van Der Pol耦合方程[13，14]。該方程為研究電液伺服系統(tǒng)的非線性動力學(xué)行為提供了結(jié)構(gòu)模型。

3　非線性耦合系統(tǒng)數(shù)值試驗

為了探索系統(tǒng)阻尼系數(shù)μ、非線性項系數(shù)βm和激振力Fn對系統(tǒng)運動特征的影響，取系統(tǒng)方程式(14)中的σ=1、ωm=0.5、ω=1、φ0=0得到具體算例式(15)，進行數(shù)值試驗研究：

(15)

3.1　分岔特性研究

Fn取不同值時，分別以μ和βm為分岔參數(shù)作分岔圖，如圖6、圖7所示。圖中橫軸分別為單位質(zhì)量上的系統(tǒng)阻尼系數(shù)μ和彈簧力非線性項系數(shù)βm，縱軸為振動位移y。

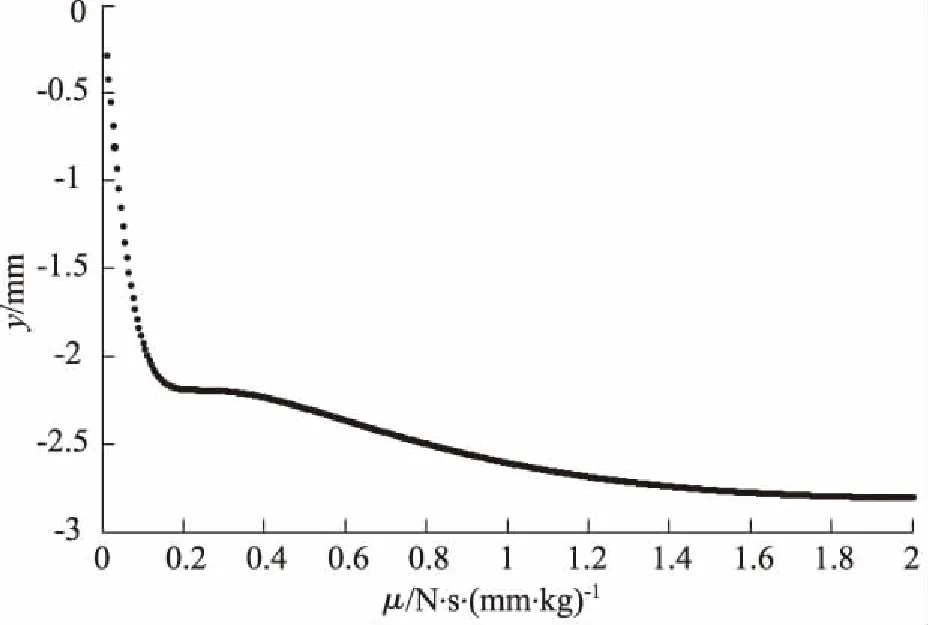
圖6　Fn=20 N·rad/(s·kg)時分岔參數(shù)為μ的分岔圖

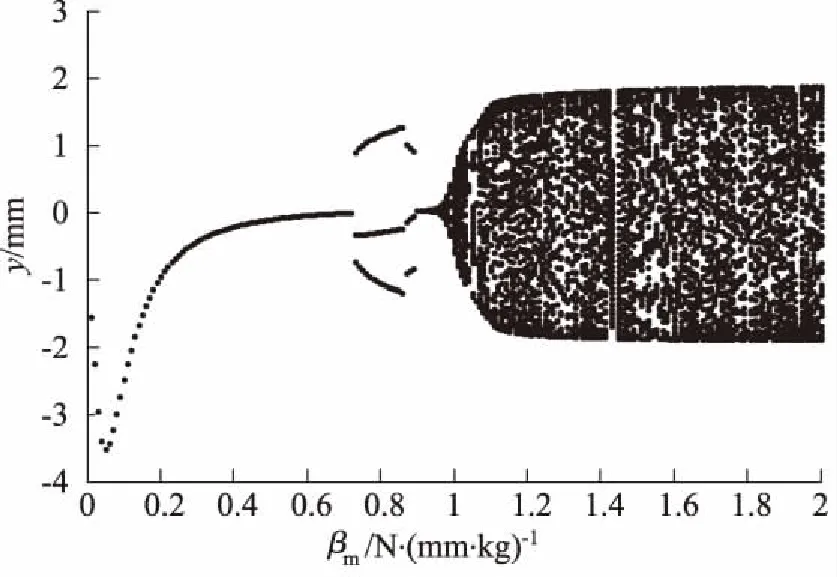
圖7　Fn=1.6 N·rad/(s·kg)時分岔參數(shù)為βm的分岔圖

由圖6、圖7可知，當(dāng)參數(shù)Fn、μ和βm取不同值時系統(tǒng)發(fā)生了不同程度的分岔現(xiàn)象[6]：① 系統(tǒng)方程存在單解、多解和無窮多個解，反映在分岔圖上表現(xiàn)為單值曲線、多值曲線和涂黑區(qū)等不同的區(qū)段，分別對應(yīng)于單周期、多周期和混沌等不同的運動狀態(tài)。② 隨著參數(shù)的變化，系統(tǒng)會發(fā)生運動狀態(tài)突然變化的動態(tài)分岔現(xiàn)象。

3.2　運動形態(tài)仿真

為了形象地體現(xiàn)系統(tǒng)在不同參數(shù)下的運動形態(tài)，在MATLAB中建立仿真模型，對其典型的非線性動力學(xué)行為進行仿真[12]。采樣頻率取100 Hz，遠大于外控力頻率：fP=ω/2π=0.16 Hz。

當(dāng)μ=2 N·s/(mm·kg)，F(xiàn)n=20 N·rad/(s·kg)時，仿真結(jié)果如圖8所示。時間歷程呈周期重復(fù)；功率譜在基頻fP及其倍頻處出現(xiàn)尖峰；相軌跡在有限的區(qū)域內(nèi)重復(fù)，呈一封閉曲線，即有極限環(huán)存在；Poincaré圖在一定的區(qū)域上只有1個孤立點存在。表明此時系統(tǒng)處于極限環(huán)型振蕩狀態(tài)。

圖8　極限環(huán)型振蕩形態(tài)

當(dāng)βm=0.75 N/(mm·kg)，F(xiàn)n=1.6 N·rad/(s·kg)時，仿真結(jié)果如圖9所示。時間歷程呈周期重復(fù)；功率譜在分頻fP/3及其倍頻處出現(xiàn)尖峰；相軌跡在有限的區(qū)域內(nèi)重復(fù)，呈封閉曲線；Poincaré圖在一定的區(qū)域上有3個孤立點存在。說明此時系統(tǒng)處于3倍周期運動狀態(tài)，周期3意味著混沌。

當(dāng)βm=1.1 N/(mm·kg)，F(xiàn)n=1.6 N·rad/(s·kg)時，仿真結(jié)果如圖10所示。時間歷程無規(guī)律；功率譜出現(xiàn)噪聲背景和寬峰；相軌跡在有限區(qū)域內(nèi)不重復(fù)；Poincaré圖在有限的區(qū)域上有無限個孤立點存在。說明此時系統(tǒng)處于混沌運動狀態(tài)[15]。

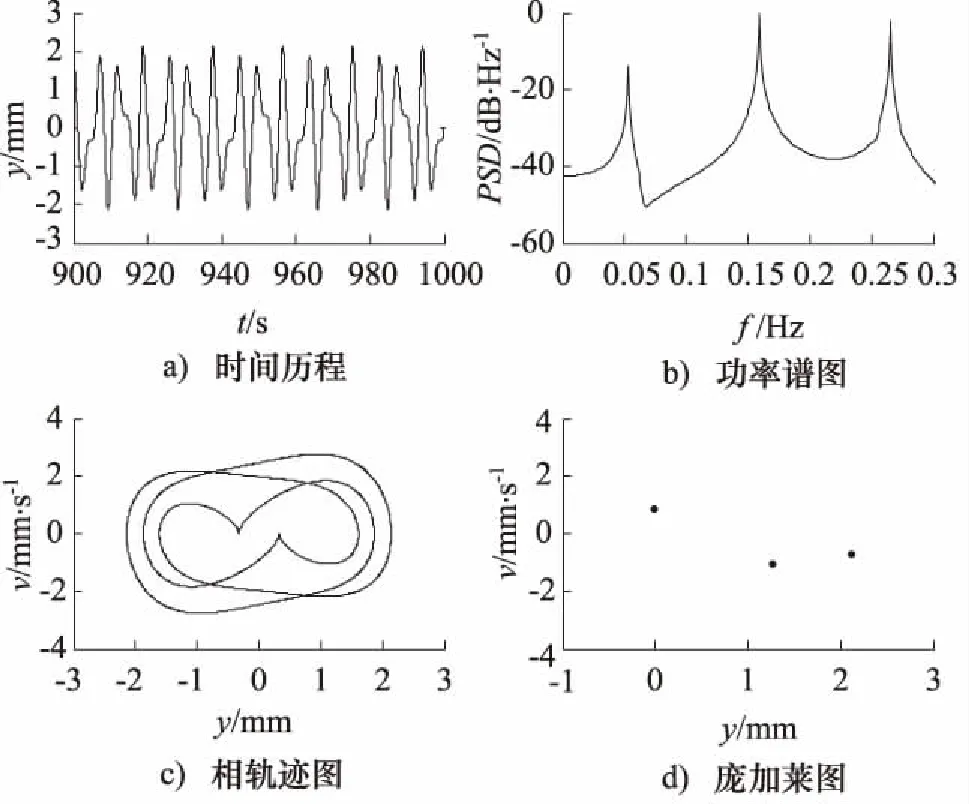
圖9　倍周期運動形態(tài)

圖10　混沌運動形態(tài)

由以上仿真分析可知，當(dāng)Fn、μ和βm取不同值時，系統(tǒng)在運行過程中蘊含豐富的非線性動力學(xué)行為，可能做極限環(huán)型振蕩、倍周期運動，進而通向混沌運動。

4　結(jié)論

以電液伺服系統(tǒng)為研究對象，根據(jù)非線性動力學(xué)原理，重點探究了彈簧力和摩擦力的非線性作用對系統(tǒng)運動特征的影響規(guī)律。通過理論研究和仿真分析，得到了如下結(jié)論：

(1) 非線性彈簧力和非線性摩擦力的耦合作用特征可以用Duffing-Van Der Pol方程來描述。

(2) 系統(tǒng)外加激振力、阻尼系數(shù)和彈簧力非線性項系數(shù)的大小影響系統(tǒng)的運動狀態(tài)。當(dāng)三者參數(shù)取不同值時，系統(tǒng)可能做極限環(huán)型振蕩、倍周期運動，進而通向混沌運動。

參考文獻：

[1]王林鴻，吳波，杜潤生，等.液壓缸運動的非線性動態(tài)特征[J].機械工程學(xué)報，2007，43(12)：12-19.

[2]Dasgupta K,Murrenhoff H.Modelling and Dynamics of a Servo-valve Controlled Hydraulic Motor by Bondgraph[J].Mechanism and Machine Theory,2011,46(7):1016-1035.

[3]Lan Z,Su J,Xu G,et al.Study on Dynamical Simulation of Railway Vehicle Bogie Parameters Test-bench Electro-hydraulic Servo System[J].Physics Procedia,2012,(33):1663-1669.

[4]Milic V,Situm Z,Essert M.Robust H∞Position Control Synthesis of an Electro-hydraulic Servo System[J].ISA Transactions,2010,49(4):535-542.

[5]Tang R,Zhang Q.Dynamic Sliding Mode Control Scheme for Electro-hydraulic Position Servo System[J].Procedia Engineering,2011,(24):28-32.

[6]Zhu Y,Jiang W L,Liu S Y,et al.Incentives of Nonlinear Dynamics Behaviors in Electro-hydraulic Servo System[J].ICIC Express Letters,2015,9(1):231-236.

[7]楊安元，楊雪.液壓系統(tǒng)的減振方法研究[J].液壓與氣動，2004，(2)：51-53.

[8]師漢民.機械振動系統(tǒng)[M].武漢：華中科技大學(xué)出版社，2004.

[9]劉秉正，彭建華.非線性動力學(xué)[M].北京：高等教育出版社，2004.

[10]朱勇，姜萬錄，王夢，等.非線性時變力作用下液壓缸爬行機理與抑制方法研究[J].農(nóng)業(yè)機械學(xué)報，2014，45(3)：305-313.

[11]王林鴻，杜潤生，吳波，等.數(shù)控工作臺的非線性動態(tài)特性[J].中國機械工程，2009，20(13)：1513-1519.

[12]姜萬錄，朱勇，鄭直. 摩擦力作用下電液伺服系統(tǒng)非線性動力學(xué)行為[J].北京航空航天大學(xué)學(xué)報,2015,41(1):50-57.

[13]Munehisa S,Naohiko I,Takashi T,et al.Analysis of Torus Breakdown into Chaos in a Constraint Duffing Van Der Pol Oscillator[J].International Journal of Bifurcation and Chaos,2008,18(4):1051-1068.

[14]李欣業(yè)，張振民，張華彪，等.Duffing-van der Pol振子的時滯反饋控制研究[J].振動與沖擊，2010，29(10):118-121.

[15]姜萬錄，張淑清，王益群.混沌運動特征的數(shù)值試驗分析[J].機械工程學(xué)報，2000，36(10)：13-17.