溫差預應力厚壁圓筒自增強分析*

朱瑞林 鄧衛軍 朱國林

(湖南師范大學工程與設計學院) （江西警察學院基礎部)

0 前言

利用機械壓力使壓力容器產生預應力以抵消部分操作應力而形成自增強壓力容器的方法，國內外做了大量研究，如文獻 [1]至文獻 [9]研究的自增強問題均是機械預應力方法的自增強。本文擬研究利用溫差使壓力容器產生預應力以抵消部分操作應力而形成自增強壓力容器的方法。

溫差預應力壓力容器比機械預應力壓力容器更安全、便捷、可靠、節省、靈活，因為溫差預應力具有如下一些特點：

（1）靠溫差應力產生預應力的方法不存在施壓介質，故沒有危險性，也不需要昂貴的水壓機等施壓設備。

（2）溫差的控制相對較為容易，因而溫差應力的大小及其均勻性容易得到保證。

（3）一旦溫差應力過大，由于不存在壓力介質，因此不至像機械應力那樣引起壓力容器爆炸等災難性事故。

（4）研究發現，溫差預應力的大小及分布規律與溫差Δt緊密聯系，因此，可根據操作條件而改變Δt以獲得不同的操作應力狀態，故容器結構優化空間很大，能夠獲得機動靈活的設計方案。

許多高壓容器在承受高壓的同時，往往還有熱量的傳遞，即筒壁內、外表面存在溫度差。由于金屬熱脹冷縮的原因，溫度較高部分金屬因受熱而產生的膨脹變形會受到溫度較低部分金屬的牽制，因而使前者受到壓縮而后者受到拉伸，從而出現溫差應力。顯然，溫差應力的大小和方向取決于溫差的大小與方向、容器的結構尺寸以及容器材料的性能，如內外壁溫差Δt=ti-to、容器材料的彈性模量E、容器材料的熱膨脹系數α、容器材料的泊松比μ、容器的徑比k=ro/ri，等等。眾所周知，厚壁圓筒的應力分布極不均勻，應力的大小和方向又取決于操作壓力的大小與方向。這就啟示人們利用溫差應力去抵消部分操作應力，從而構建一種溫差預應力自增強厚壁圓筒。

不難預見，改變溫差的大小與方向即可獲得不同的溫差應力分布狀態，而不同的溫差應力分布狀態顯然適合于不同的操作狀態。下面首先對溫差應力進行分析。

1 溫差應力分析

依據文獻[9]，可導出圓筒形壓力容器內、外壁存在溫差Δt時，器壁中任一點處 （半徑為r）的溫差應力為：

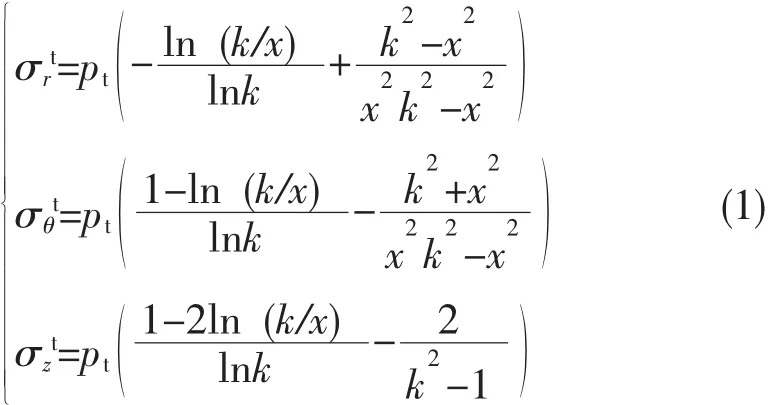
pt——熱載荷，MPa;

E——容器材料的彈性模量，MPa；

α——容器材料的熱膨脹系數，°C-1；

μ——容器材料的泊松比，無量綱；

Δt——容器內、外壁的溫差，°C；

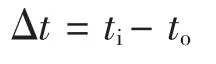
Δt＞0 時稱為內加熱， Δt＜0 時稱為外加熱；

ti——容器內壁面溫度，°C；

to——容器外壁面溫度，°C；

k——容器的徑比，無量綱；

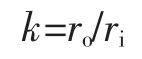
ri——容器內壁面半徑，m；

ro——容器外壁面半徑，m；

x——相對位置，x=r/ri，無量綱。

由式 （1）可見，不論內加熱還是外加熱，在圓筒壁中任一點都有：

內、外壁溫差應力為：

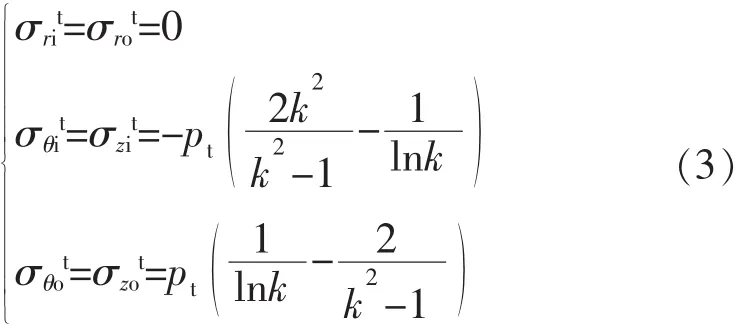
內壁面數值加下標i，外壁面數值加下標o。根據式 （1），不論內加熱或外加熱，x=k，即r=ro時，即x=1， 即 r=ri時，即即在圓筒內、外壁上軸向、環向溫差應力相等，徑向溫差應力為0。在1≤x≤k 內，有唯一極值點 （橫坐標）：

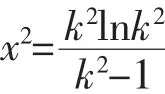
而在 1≤x2≤k2內，當 Δt＞0 時，＞0； 當 Δt＜0時，＜0。故 Δt＞0 （內加熱） 時，為極小值， 即亦即Δt＜0 （外加熱）時，為極大值， 即亦即

又根據式 （3）， 有

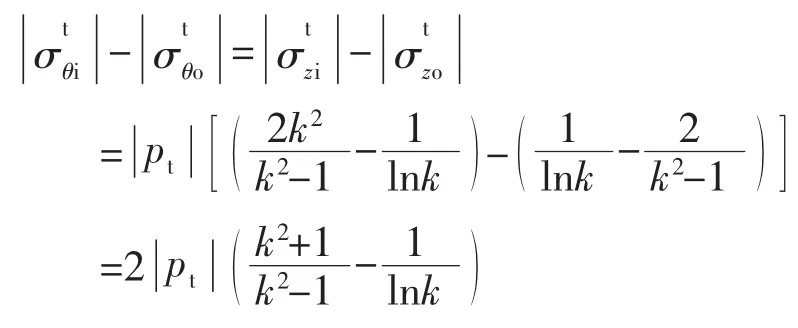
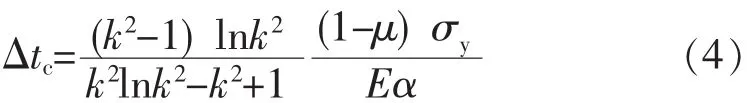
式中 σy——壓力容器材料的屈服強度。

Δt＜Δtc時，溫差應力不至于使容器產生屈服。隨著溫差增大，當Δt=Δtc時，內壁面開始屈服；溫差進一步增大，屈服區向外擴展，形成近內壁部分為塑性區、近外壁部分為彈性區的彈塑性狀態，這時彈、塑性區的應力將重新分布，不再由式 （1）表達，本文不涉及。外加熱時，臨界溫差Δtc符號與式 （4） 相反。

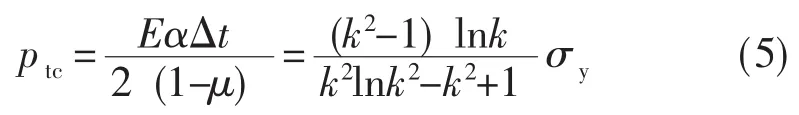
外加熱時臨界熱載荷符號與式 （5）相反。

2 利用溫差應力進行自增強的算例

例1 一般鋼材的彈性模量為E=1.95×105MPa，泊松比為μ=0.3，熱膨脹系數為α=1.2×10-5℃-1，屈服強度為σy=300 MPa。設容器k=2.5。若Δt=50°C，其溫差應力如圖1所示。

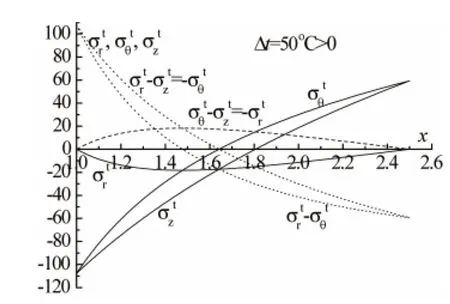
圖1 Δt=50°C的溫差應力分布

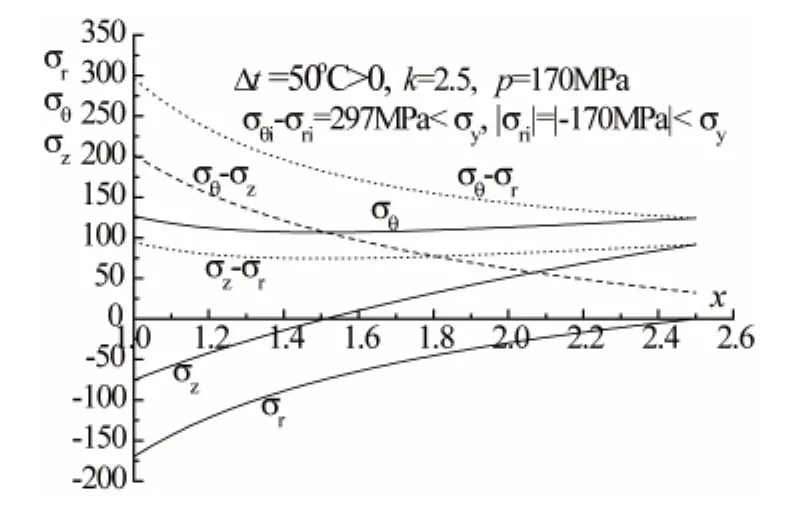
圖2 p=170 MPa、Δt=50°C時總應力分布

若對該容器施以Δt=50℃ （內壁面比外壁面高50℃）的溫差，其承載能力可達p=170 MPa。p=170 MPa、Δt=50℃時，徑向、環向、軸向總應力 （溫差應力與機械應力疊加）σr、σθ、σz如圖2所示。由圖2可見，此時容器處于安全狀態。

假如溫差增大到臨界溫差Δtc，由式 （4）得內加熱時臨界溫差Δtc=139.181℃，其承載能力可達p=250 MPa。 p=250 MPa、 Δt=Δtc時， 總應力 σr、σθ、σz如圖3所示。由圖3可見，此時容器仍處于安全狀態。

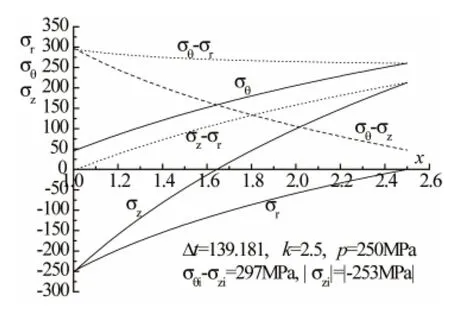
圖3 p=250 MPa、Δt=Δtc時總應力分布

例2 容器各性能參數仍如例1所述，不同之處為外加熱。

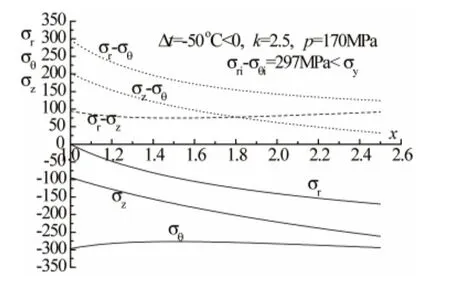
圖4 p=170 MPa、Δt=-50°C時總應力分布

Δt=Δtc=-139.181℃時的溫差應力如圖5所示，但對外壓容器而言，增大或減小溫差不一定有利于提高承載能力。例如，Δt=Δtc=-139.181°C、p=170 MPa 時， σθo=-400 MPa； Δt=-40 ℃、 p=170 MPa時， σθi=-319 MPa，σri-σθi=319 MPa。 這些應力均超過強度極限，好在外壓厚壁圓筒在實際使用中較為少見。

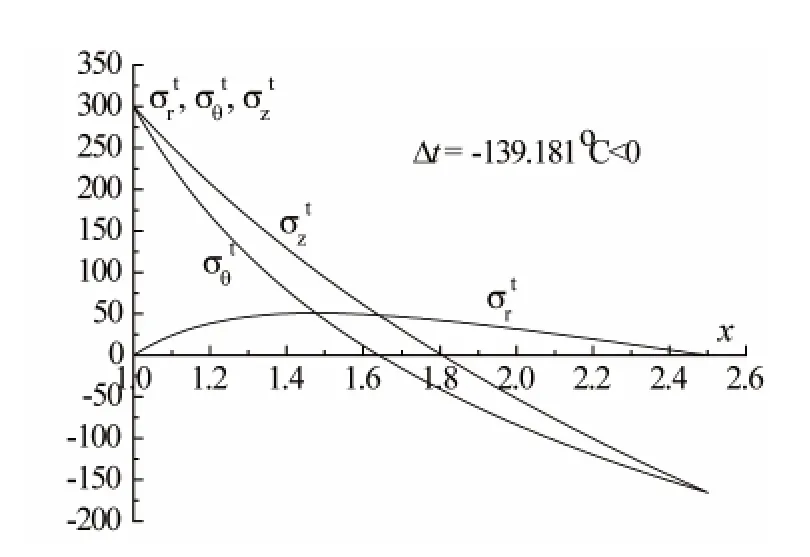
圖5 Δt=Δtc=-139.181℃的溫差應力分布

假如某生產過程不可避免地存在Δt=-40℃的溫差，根據以上分析，此時容器的承載能力為p=160 MPa。假如某生產過程不可避免地存在Δt=-100℃的溫差，根據以上分析，此時容器的承載能力為p=105 MPa，小于最大彈性載荷pe。

3 結論

本文在分析溫差應力特性的基礎上，研究了借溫差應力產生預應力的厚壁壓力容器自增強方法，指出了溫差等因素對厚壁壓力容器承載能力的影響。綜上所述，有如下結論：

（2）不論是內加熱還是外加熱，內壁面應力絕對值大于外壁面應力絕對值，隨著溫差 Δt增大，總是內壁面先于外壁面屈服。

（3）內加熱有利于降低內壓操作容器的應力，外加熱有利于降低外壓操作容器的應力。但并非溫差 Δt越大越有利。

（4）當生產過程不可避免地存在溫差時，可調節壁厚與承載能力，以保證容器的安全性。

[1] Ali A R M,Ghosh N C,Alam T E.Optimum design of pressure vessel subjected to autofrettage process[J].World Academy of Science,Engineering and Technology,2010,46：667-672.

[2] Hojjati M H,Hassani A.Theoritical and finite element modeling of autofrettage process in strain hardening thickwalled cylinders[J].International Journal of Pressure Vessels and Piping,2007,84：310-319.

[3] Majzoobi G H，Farrahi G H，Mahmoudi A H.A finite element simulation and an experimental study of autofrettage for strain hardened thick-walled cylinders[J].Materials Science and Engineering A 359,2003：326-331.

[4] Perry J,Aboudi J.Elasto-plastic stresses in thick walled cylinders[J] .ASME JournalofPressure Vessel Technology,2003,125：248-252.

[5] 朱瑞林，朱國林.自增強圓筒塑性區深度和承載能力探討 [J].化工裝備技術,2012,33(3)：35-39.

[6] Zhu Ruilin,Zhu Guolin.Effect of optimum plastic depth on stresses and load-bearing capacity of autofrettaged cylinder[J].Chinese Journal of Mechanical Engineering,2013,26(2)：365-370.

[7] Zhu Ruilin.Study on autofrettage for medium-thick pressure vessels [J].Journal of Engineering Mechanics,2013,139(12)：1790-1796.

[8] Zhu Ruilin,Zhu Guolin.On autofrettage of cylinders by limiting circumferential residual stress based on mises yield criterion[J].Journal of Theoretical and Applied Mechanics,2013,51(3)： 697-710.

[9] 余國琮.化工容器及設備 [M].北京：化學工業出版社，1980.