對一道三角形面積最值題的解法探討
2015-04-10 13:53:48樊啟滿
新課程(下) 2015年11期
樊啟滿
(江西省修水縣職業高中)
原題:在△ABC中,內角A,B,C的對邊分別為a,b,c,其外接圓半徑為6,且a+c=16.求△ABC面積的最大值.
此題是甘志國老師率先提出,他在《數學通訊》論壇里發了他的解法,引起了不小的爭論。解法如下:由正弦定理及題設可得BA+BC=16,所以點B在以A,C為焦點、長軸長為16 的橢圓上,當點B從短軸的端點向長軸的端點移動時,△ABC的面積S在減小.不妨設點B在橢圓弧上運動且∠BAC是銳角,得S隨∠BAC的減小而減小.
事實上底邊AC的長是隨著點B的位置不同而變化的,而設AC的長不變,解出的結果似有不妥.
我的解法:
由于圓內接三角形的對稱性,當AB取一有定義時的值時,對應著四種三角形(如圖),解此題只需考慮這種情況:即固定A點,A,B,C三點在圓上按順時針方向排列.它又分為兩種情況:點B在AO連線下方與點B在AO連線上方.
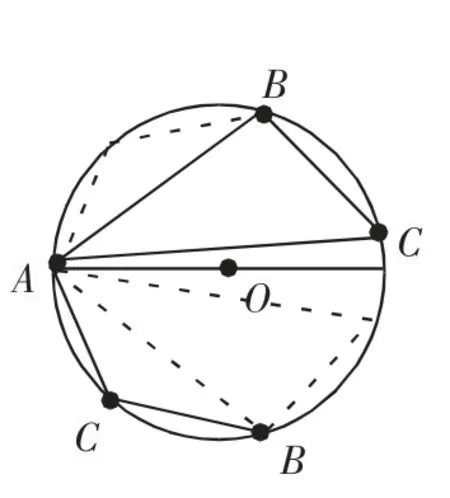
當點B在AO連線上及其下方時,面積的最小值為0,最大值為,此種情況不再贅述.下面只考慮另一種點B在AO連線上及其上方的情況:
當AB=4 時,角B最小,角A為直角;當時,角B為直角;當AB=8 時,角B最大,為鈍角.
設AB=8-m,則m的范圍為(-4≤m≤4),所以BC=8+m,三角形ABC的面積為:
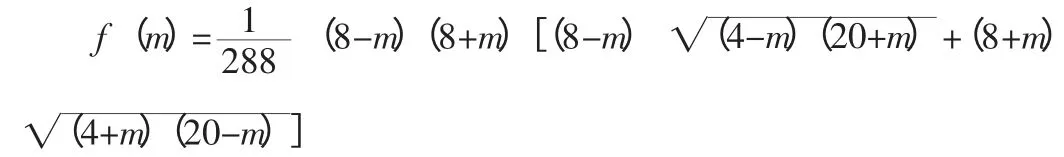
顯然這個函數是個偶函數,只需證明m∈[-4,0]上的單調性即可.
所以f(m)在上一定是增函數,函數值最大為28.
由于y1=(8-m)(8+m)在上是增函數,而y2=sinB在上是減函數,
考慮到g(m)=sinB,當時是減函數,且值域為時也是減函數,且值域為且恒有時
∵F(′m)時,F′(m)≥0,(fm)在m∈上是增函數,結合第一種情況,△ABC面積的最大值為

