超臨界層流復(fù)合翼飛機Re數(shù)效應(yīng)修正方法研究

馮文梁，陳 斌，呂凌英

(成都飛機工業(yè)(集團)有限責(zé)任公司技術(shù)中心，四川成都 610092)

超臨界層流復(fù)合翼飛機Re數(shù)效應(yīng)修正方法研究

馮文梁*，陳 斌，呂凌英

(成都飛機工業(yè)(集團)有限責(zé)任公司技術(shù)中心，四川成都 610092)

基于γ-Reθ轉(zhuǎn)捩預(yù)測模型，對使用超臨界層流復(fù)合翼的飛機進行轉(zhuǎn)捩預(yù)測數(shù)值模擬。獲得機翼在不同Re數(shù)下的自由轉(zhuǎn)捩位置，計算轉(zhuǎn)捩位置與試驗數(shù)據(jù)吻合。結(jié)合轉(zhuǎn)捩預(yù)測結(jié)果和強制轉(zhuǎn)捩試驗數(shù)據(jù)，對全機風(fēng)洞試驗數(shù)據(jù)進行不同高度的Re數(shù)效應(yīng)修正。改變了戰(zhàn)斗機只對阻力進行Re數(shù)效應(yīng)修正的傳統(tǒng)方法，分別對飛機的升力、阻力及縱向力矩進行Re數(shù)效應(yīng)修正。

Re數(shù)效應(yīng);轉(zhuǎn)捩;γ-Reθ模型

0 引言

風(fēng)洞試驗一般使用縮比模型，風(fēng)洞模型的縮小以及風(fēng)洞固有特性的限制，使得風(fēng)洞試驗的Re數(shù)與飛機真實飛行Re數(shù)存在較大的差異。因此必須對風(fēng)洞試驗數(shù)據(jù)進行Re數(shù)效應(yīng)修正。

對戰(zhàn)斗機的Re數(shù)效應(yīng)研究表明，由于戰(zhàn)斗機多采用較薄的翼型，在大氣中飛行時，機翼附面層近似于全湍流。Re數(shù)對全機的升力特性和縱向力矩特性影響很小，而對表面磨擦阻力有較大的影響。因此，在試驗數(shù)據(jù)修正中，只對阻力做Re數(shù)修正，包括最小阻力和升致阻力。

現(xiàn)今民機和高空、高速無人機等，為追求高的巡航效率，一般采用高升阻比翼型，如超臨界翼型和超臨界層流復(fù)合翼型。這些翼型在設(shè)計點(巡航狀態(tài))均能保持不小于50%弦長的自然層流區(qū)。研究表明，在設(shè)計狀態(tài)下層流翼型的阻力比普通紊流翼型的阻力可以減小一倍以上。但當(dāng)偏離設(shè)計點較多時，自然層流區(qū)趨于消失。翼型的阻力會迅速增大。同時試驗研究也表明，雷諾數(shù)通過影響超臨界翼型的流場結(jié)構(gòu)和壓力分布，進而影響超臨界翼型的宏觀氣動力特性，包括升力、阻力及縱向力矩［1］。雷諾數(shù)對超臨界翼型流動影響同時反應(yīng)在轉(zhuǎn)捩位置上。轉(zhuǎn)捩是邊界層理論中非常重要的概念，表示由層流流動向湍流流動的轉(zhuǎn)變［2-5］。

戰(zhàn)斗機的Re數(shù)效應(yīng)修正方法是通過變Re數(shù)試驗，得到最小阻力隨Re數(shù)變化的線性曲線，采用外插的方法把試驗Re數(shù)的最小阻力修正到飛行Re數(shù)。

本文通過基于γ-Reθ的轉(zhuǎn)捩預(yù)測模型對飛機機翼進行數(shù)值模擬，得到不同Re數(shù)下機翼的自由轉(zhuǎn)捩位置。同時在風(fēng)洞試驗中對飛機機翼進行強制轉(zhuǎn)捩試驗，得到機翼不同轉(zhuǎn)捩位置的氣動數(shù)據(jù)。利用CFD計算得到的轉(zhuǎn)捩位置結(jié)合強制轉(zhuǎn)捩試驗數(shù)據(jù)，對風(fēng)洞試驗數(shù)據(jù)的升力、阻力和縱向力矩進行Re數(shù)效應(yīng)修正［6-11］。

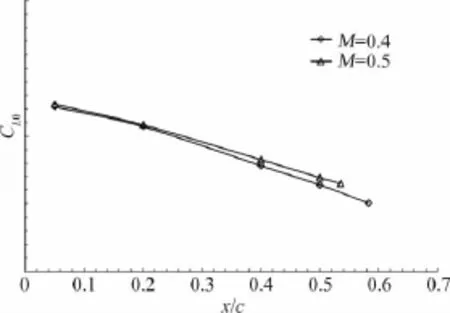
圖1 零迎角升力系數(shù)與轉(zhuǎn)捩位置關(guān)系Fig.1 The relationship between lift coefficient (α=0)and transition positions

1 計算軟件簡介

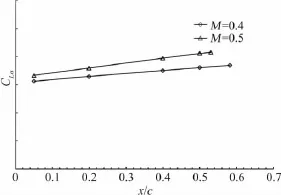
圖2 升力線斜率與轉(zhuǎn)捩位置關(guān)系Fig.2 The relationship between lift slope and transition positions

本文采用在航空航天行業(yè)使用較多的商用CFD軟件ANSYS CFX，該軟件采用基于有限元的有限體積法，使用全隱式多網(wǎng)格耦合求解，對六面體網(wǎng)格采用24點插值，本文計算模型采用六面體網(wǎng)格，網(wǎng)格數(shù)約為1 000萬左右。

本文中物體表面設(shè)置為無滑移物面邊界條件，遠場設(shè)置為開放邊界條件，選取SST湍流模型。轉(zhuǎn)捩模型采用γ-Reθ轉(zhuǎn)捩預(yù)測模型，由于該模型得到較為成熟的應(yīng)用，本文在此不再贅述，見文獻［12-15］。

2 強制轉(zhuǎn)捩試驗

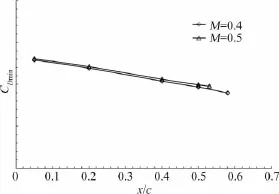
圖3 最小阻力與轉(zhuǎn)捩位置關(guān)系Fig.3 The relationship between minimum drag and transition positions

為研究機翼不同轉(zhuǎn)捩位置對氣動特性的影響，在機翼表面不同位置粘貼金剛砂膠帶進行強制轉(zhuǎn)捩風(fēng)洞試驗。根據(jù)試驗結(jié)果顯示，最小阻力、零迎角升力、升力線斜率、零升力矩以及縱向安定導(dǎo)數(shù)隨著轉(zhuǎn)捩位置的變化基本呈線性變化。

M=0.4、0.5、0.6的試驗Re數(shù)分別1.21×106、1.45×106、1.77×106。從圖1～圖5可以看出，不同馬赫數(shù)(Re也不同)，在相同強制轉(zhuǎn)捩位置，氣動特性略有差異。因此在進行Re數(shù)效應(yīng)修正時，首先通過CFD計算得到某馬赫數(shù)下不同高度的機翼 轉(zhuǎn)捩位置，再根據(jù)計算轉(zhuǎn)捩位置，在圖1～圖5中找到相應(yīng)馬赫數(shù)和轉(zhuǎn)捩位置的縱向?qū)?shù)值來進行Re數(shù)效應(yīng)修正。

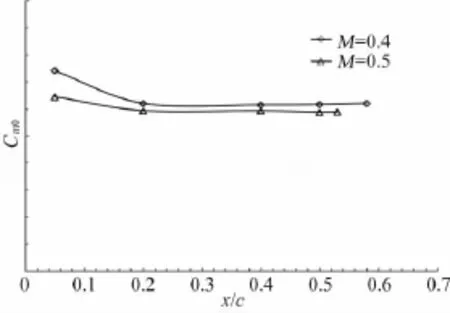
圖4 零升力矩與轉(zhuǎn)捩位置關(guān)系Fig.4 The relationship between zero lift pitching moment and transition positions

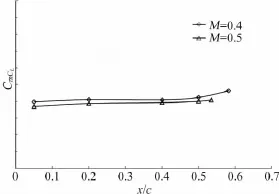
圖5 縱向力矩導(dǎo)數(shù)與轉(zhuǎn)捩位置關(guān)系Fig.5 The relationship between pitching moment derivative and transition positions

3 機翼超臨界特性

機翼初期設(shè)計考慮到高升阻比以及高臨界馬赫數(shù)的要求，選取了超臨界層流復(fù)合的翼型。后期由于飛機指標(biāo)改變，飛行速度降低，沒有使用到機翼的超臨界特性，因此風(fēng)洞試驗沒有完全驗證其超臨界特性(臨界馬赫數(shù))。

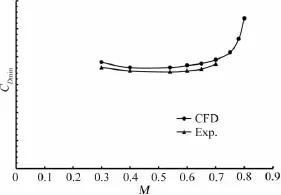
圖6 機翼最小阻力隨馬赫數(shù)變化曲線Fig.6 The curves for minimum drag of wing and Mach number

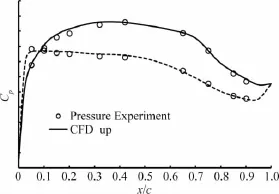
圖7 M=0.65，α=0°機翼截面壓力分布Fig.7 The pressure distribution of some wing section (M=0.65，α=0°)

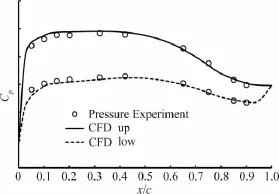
圖8 M=0.65，α=3°機翼截面壓力分布Fig.8 The pressure distribution of some wing section (M=0.65，α=3°)

4 計算與試驗對比

機翼自由轉(zhuǎn)捩位置較難通過試驗直接得到，本文在風(fēng)洞試驗中進行機翼不同位置的強制轉(zhuǎn)捩試驗，得到不同轉(zhuǎn)捩位置與縱向?qū)?shù)關(guān)系曲線(圖1～圖5)，并將自由轉(zhuǎn)捩試驗得到的縱向?qū)?shù)在圖1～圖3中進行線性外插，從而得到機翼自由轉(zhuǎn)捩位置。

由于風(fēng)洞Re數(shù)變化范圍較小，因此只有Re低于2.5×106的試驗數(shù)據(jù)。計算大氣條件與試驗相同，從圖9可以看出，機翼計算自由轉(zhuǎn)捩位置較試驗靠后約2%當(dāng)?shù)叵议L，計算轉(zhuǎn)捩位置與試驗結(jié)果隨Re變化的趨勢相同，計算結(jié)果與試驗數(shù)據(jù)基本吻合。

圖10～圖12為不同Re數(shù)的機翼上表面間歇因子云圖，從圖中可以看出間歇因子在層流段幾乎為零，達到轉(zhuǎn)捩位置后間歇因子瞬間增大。從圖中可以看出，機翼內(nèi)段由于受到機身繞流的影響層流段較外翼短，轉(zhuǎn)捩位置沿展向分布也不均勻。

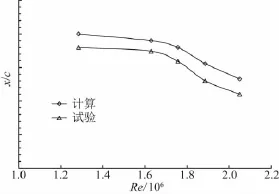
圖9 試驗與計算轉(zhuǎn)捩位置對比Fig.9 The transition positions comparing for calculation and experiment

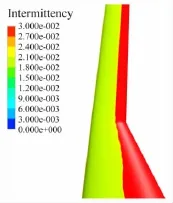
圖10 Re=2.0×106間歇因子云圖Fig.10 The intermittent factor contour for Re=2.0×106

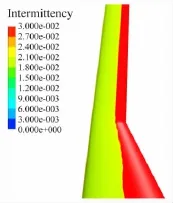
圖11 Re=5.0×106間歇因子云圖Fig.11 The intermittent factor contour for Re=5.0×106

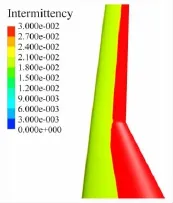
圖12 Re=8.0×106間歇因子云圖Fig.12 The intermittent factor contour for Re=8.0×106

5 Re數(shù)效應(yīng)修正方法

根據(jù)飛機飛行包線，確定飛機的飛行Re數(shù)范圍，并對該范圍的Re數(shù)進行數(shù)值模擬，計算出不同高度、速度下的轉(zhuǎn)捩位置。由于計算轉(zhuǎn)捩位置較試驗有約2%當(dāng)?shù)叵议L的誤差，對計算轉(zhuǎn)捩位置進行一定的修正。

由CFD計算得到的不同Re數(shù)的機翼轉(zhuǎn)捩位置，并根據(jù)各縱向?qū)?shù)與轉(zhuǎn)捩位置的線性關(guān)系(圖1～圖5)，使用計算得到的轉(zhuǎn)捩位置進行線性插值得到對應(yīng)Re數(shù)的縱向?qū)?shù)。用插值縱向?qū)?shù)減去試驗值，得到Re數(shù)效應(yīng)修正的縱向?qū)?shù)增量，并通過計算得到Re數(shù)修正量。

具體修正公式如下:

不同馬赫數(shù)和Re數(shù)下的計算自由轉(zhuǎn)捩位置如圖13。從圖中可以看出，在Re數(shù)小于7×106時，轉(zhuǎn)捩位置基本不變，超過該Re數(shù)后，轉(zhuǎn)捩位置急劇前移，層流段變短。

風(fēng)洞試驗僅能做到試驗?zāi)Ｐ秃退俣扰c飛機真實飛行相似，而無法得到飛機在不同高度下的氣動數(shù)據(jù)。飛機不同的飛行高度反應(yīng)了飛機Re數(shù)的變化。為獲取飛機在不同高度下的氣動數(shù)據(jù)，必須對風(fēng)洞試驗數(shù)據(jù)進行Re數(shù)效應(yīng)修正。

圖14～圖15為不同高度進行Re數(shù)修正后的極曲線和俯仰力矩曲線。圖16為經(jīng)過Re數(shù)修正后的風(fēng)洞試驗數(shù)據(jù)與飛行試驗氣動數(shù)據(jù)的對比。飛行試驗的升阻力通過飛機飛行過程中的重量以及發(fā)動機推力進行反算得到，從圖中可以看出，飛行試驗數(shù)據(jù)與風(fēng)洞試驗Re數(shù)修正數(shù)據(jù)基本吻合，試驗數(shù)據(jù)與修正數(shù)據(jù)的差異是由于發(fā)動機推力損失無法準確獲取等因素造成。

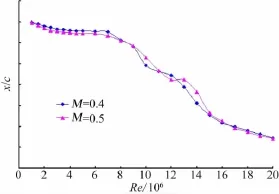
圖13 CFD計算轉(zhuǎn)捩位置隨Re變化曲線(M=0.5)Fig.13 The curves of CFD transition positions and Re(M=0.5)

圖14 進行Re數(shù)修正后的升阻極曲線Fig.14 The lift-drag polar curves after Reynolds number effect correction

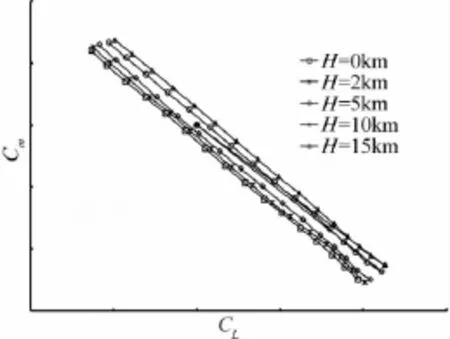
圖15 進行Re數(shù)修正后的力矩曲線Fig.15 The pitching moment curves after Reynolds number effect correction

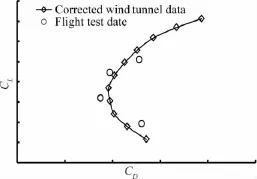
圖16 Re數(shù)修正數(shù)據(jù)與飛行試驗數(shù)據(jù)升阻極曲線對比Fig.16 The comparing for the data after Reynolds number effect correction and flight tests

6 結(jié)論

通過轉(zhuǎn)捩位置預(yù)測結(jié)合強制轉(zhuǎn)捩風(fēng)洞試驗的Re數(shù)效應(yīng)修正方法，使得風(fēng)洞試驗數(shù)據(jù)更加準確、可靠。修正方法已應(yīng)用于超臨界層流復(fù)合翼飛機的Re數(shù)效應(yīng)修正中，并得到飛行試驗的驗證，可為同類飛機的風(fēng)洞試驗數(shù)據(jù)Re數(shù)效應(yīng)修正提供可靠的修正方法。

［1］ Xu Xin，Liu Dawei，Chen Dehua，et al.Analysis of llow over supercritical airfoil for Reynolds numbers effects［R］.CSTAM 2012-B03-0140，2012.(in Chinese)

許新，劉大偉，陳德華，等.超臨界翼型雷諾數(shù)影響流動分析［R］.CSTAM 2012-B03-0140，2012.

［2］ Chen Yinchun，Si Jiangtao，Han Xianli，et al.Investigation of transition effect on the pressure distribution of supercritical wing［J］.Acta Aerodynamica Sinica，2003，21(4):470-475.(in Chinese)

陳迎春，司江濤，韓先鋰，等.轉(zhuǎn)捩對超臨界機翼壓力分布的影響分析［J］.空氣動力學(xué)學(xué)報，2003，21(4):470-475.

［3］ Yang Qingzhen，Zhang Zhongyin.Analysis of the boundary layer and aerodynamic characteristics of a supercritical laminar wing［J］.Acta Aeronautica et Astronautica Sinica，2004，25(5):439-442.(in Chinese)

楊青真，張仲寅.超臨界層流機翼邊界層及氣動特性分析［J］.航空學(xué)報，2004，25(5):439-442.

［4］ Chen Yi，Gao Zhenghong.Application of gamma-theta transition model to flows around airfoils［J］.Acta Aerodynamica Sinica，2009，27(4):411-418.(in Chinese)

陳奕，高正紅.Gamma-Theta轉(zhuǎn)捩模型在繞翼型流動問題中的應(yīng)用［J］.空氣動力學(xué)學(xué)報，2009，27(4):411-418.

［5］ David B DeGraff，Donald R Webster，John K Eaton.The effect of Reynolds number on boundary layer turbulence［J］.Experimental Thermal and Fluid Science，1999，18:341-346.

［6］ Suzen Y，Huang P.Modeling of flow transition using an intermittency transport equation［J］.Journal of Fluids and Engineering，2000，122(2):273-284.

［7］ Suzen Y B，Xiong G，Huang P G.Prediction of transition flows in a low-pressure turbine using an intermittency transport equation［R］.AIAA 2000-2645.

［8］ Zhang Yulun，Wang Guangxue，Meng Dehong，et al.Calibration of γ-Reθtransition model［J］.Acta Aerodynamica Sinica，2011，29 (3):295-301.(in Chinese)

張玉輪，王光學(xué)，孟德宏，等.γ-Reθ轉(zhuǎn)捩模型的標(biāo)定研究［J］.空氣動力學(xué)學(xué)報，2011，29(3):295-301.

［9］ Langtry R B，Menter F R.Transition modeling for general CFD applications in aeronautics［R］.AIAA 2005-522.

［10］Mayle R E.The role of laminar-turbulent transition in gas turbine engines［J］.ASME Journal of Turbo Machinery，1991，113:509-537.

［11］Langtry R B，Menter F R，Likki S R，et al.A correlation based transition model using local variables:part II-test case and industrial application［R］.ASME-GT 2004-53454，ASME Turbo Expo 2004 Vienna Austria，2004.

［12］Menter F R，Langtry R B，Likki S R，et al.A correlation based transition model using local variables:part I-model formulation［R］.ASME-GT 2004-53452.ASME Turbo Expo 2004 Vienna Austria，2004.

［13］Langtry R B.A correction-based transition model using local variables for unstructured parallelized CFD codes［D］.［PhD Thesis］.Stuttgart，2006.

［14］ Poll D I A.Laminar to turbulent transition［C］//IUTAM SYM.1979:253-260.

［15］ Erik J，Ponnampalam B.On the stability of three-dimensional boundary layers，Part 1:Linear and non-linear instiblity［R］.I2-CASE Report 99219.1999.

Research Reynolds number effect correction for air supercritical laminar complex wing

Feng Wenliang*，Chen Bin，Lyu Lingying
(Technical Center of Chengdu Aircraft Industrial(Group)Co.Ltd，Chengdu 610092，China)

Transition significantly affects aerodynamic characteristics of an airplane，such as the drag，lift and pitching moment，and the transition position of supercritical laminar complex wings is greatly influenced by Reynolds number effect.The traditional methods of Reynolds number effect correction are not suitable anymore for those aircraft with supercritical laminar complex wings.A γ-Reθmodel for the transition prediction of an airplane with supercritical laminar complex wings is introduced.The transition point could be obtained by this way according to its Reynolds number，and the computational transition points are accord with the wind tunnel tests.The wind tunnel experiment data are corrected and modified by the combination of CFD results and experiment data.The traditional Reynolds number effect correction methods correct the drag only，while this new proposed method corrects the lift，drag and pitching moment respectively and simultaneously.More accurate data for real flight could be obtained from wind tunnel experiment data by this method，and makes the flight safer.

Reynolds number effect;transition;γ-Reθmodel

V211.3

A

10.7638/kqdlxxb-2013.0086

0258-1825(2015)04-0470-05

2013-09-04;

2014-01-24

馮文梁*(1981-)，男，重慶人，工程師，研究方向:氣動布局設(shè)計，計算流體力學(xué).E-mail:78456365@qq.com

馮文梁，陳斌，呂凌英.超臨界層流復(fù)合翼飛機Re數(shù)效應(yīng)修正方法研究［J］.空氣動力學(xué)學(xué)報，2015，33(4):470-474.

10.7638/kqdlxxb-2013.0086 Feng W L，Chen B，Lyu L Y.Research Reynolds number effect correction for air supercritical laminar complex wing［J］.Acta Aerodynamica Sinica，2015，33(4):470-474.