基于高階物面近似的自適應間斷有限元法歐拉方程數值模擬

孫 強，呂宏強，伍貽兆

(南京航空航天大學，航空宇航學院，江蘇南京 210016)

基于高階物面近似的自適應間斷有限元法歐拉方程數值模擬

孫 強，呂宏強*，伍貽兆

(南京航空航天大學，航空宇航學院，江蘇南京 210016)

將高階間斷有限元與網格自適應相結合，于非結構網格上求解二維Euler方程。將數值解多項式的高階項貢獻用人工粘性項系數的形式進行量化，網格自適應過程中以人工粘性項系數作為網格自適應的指示器。在系數達到設定的上限閥值的區域進行網格加密，在系數達到設定的下限閥值的區域將迭代過程中加密過的網格稀疏以減少網格量。所有自適應均在高階曲線逼近真實物面的基礎上進行，以保證數值結果的精度。典型數值算例結果與實驗結果進行了對比，表明采用該自適應間斷有限元法可以保證以盡可能小的計算量得到高精度結果。

高階間斷有限元;自適應方法;Euler方程;人工粘性;物面高階近似

0 引言

間斷Galerkin有限元法(DGM)發展于20世紀70年代［1］。由于該方法能夠構造高精度的格式，并且易于實現自適應計算和并行計算，已成為計算流體力學領域研究熱點之一。Bassi等在1997年用DGM成功求解了二維Euler方程和N-S方程［2-3］;Cockburn等提出Runge-Kutta間斷Galerkin方法(RKDG)［4-5］; Nguyen等將S-A湍流模型成功應用于DGM［6］。國內呂宏強等在稀疏的非結構網格上求解了二維Euler方程和線化Euler方程［7-9］;張來平等發展了靜動態混合重構的DG/FV混合格式［10］;于劍等對人工粘性和NS方程進行了研究［11-12］。

自適應方法根據研究對象的不同和解的性質自動調整網格分布或者數值解的逼近精度。在流體力學計算中，解通常在局部變化較大，其他大部分區域是光滑的［12］，此時使用自適應方法可以有效降低計算量。自適應方法通常被分為三類:對局部網格加密或稀疏的h型自適應;調整局部單元內逼近多項式次數的p型自適應;調整網格單元位置保持單元總數不變的r型自適應。

由于間斷有限元方法通常將未知數表達為高階形式，在相同的網格上計算量與有限體積法和有限差分法相比成倍增加，故而自適應方法與間斷有限元方法相結合勢在必行。Yang等提出了一種于非結構網格上模擬界面的自適應方法［13］;Flaherty和Remacle研究小組則首次將網格度量場引入自適應間斷有限元方法中［14］。徐云、吳迪、蔚喜軍［15-16］等則根據后誤差估計提出了不同的h型網格自適應方法。

在高階情況下(p≥2)，間斷有限元對于物面形狀的表達十分敏感［3］，若物面邊界以直線表達，則無法得到收斂解。本文設計了一種h型自適應高階間斷有限元法，物面邊均采用高階曲線逼近真實物面以保證數值解的精度。將數值解多項式的高階項貢獻以人工粘性［17］系數ε的形式量化，以系數ε作為網格自適應的指示器。數值模擬過程中產生的非線性方程組采用牛頓法進行迭代，每個迭代步產生的大型線性系統采用塊高斯-賽德爾方法求解［18］。

1 間斷有限元數值離散

二維守恒形式的Euler方程為

其中，U為守恒變量，對流通量F(U)=(f(U)，g (U))，表達式分別為:

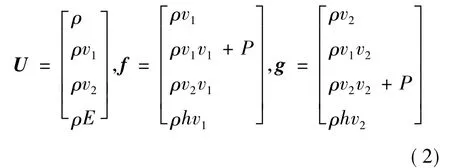
式中，ρ為密度;v1和v2為x、y方向的速度分量;E為單位總能;P為壓強;h為單位總焓。

式(1)兩邊乘檢驗函數V，在計算域運用分部積分后，弱解形式為:

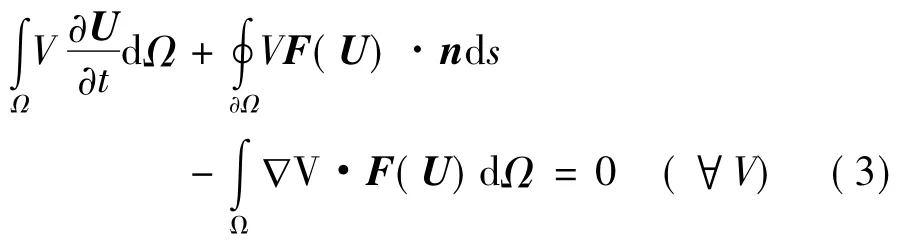
將計算域劃分為網格{e}，其中e表示網格單元。在每個單元e內:

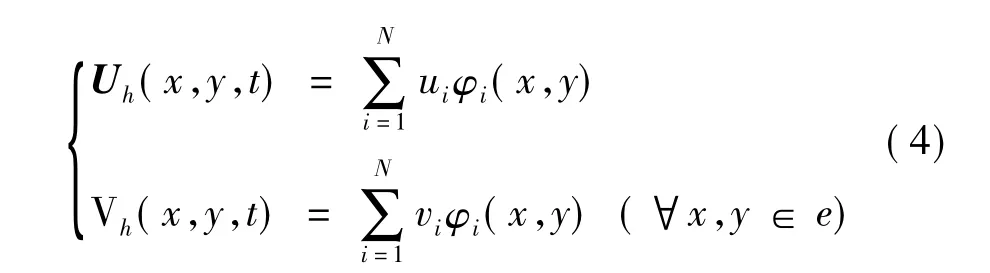
式(4)中，φi(x，y)為基函數。將式(4)代入式(3)中，得

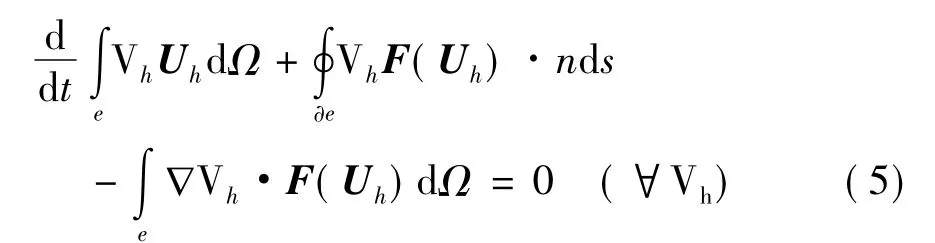
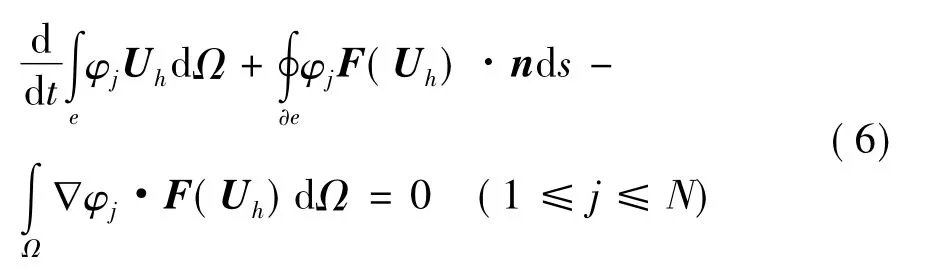
式(6)稱為p階間斷有限元離散［7］，p為式(4)中基函數的階數。

由于間斷有限元法允許解在單元的邊界處不連續，因而數值通量的定義不是唯一的。此處的數值通量直接借用傳統有限體積法的處理方法，即將式(6)中的通量函數F(Uh)·n用數值通量代替，其中和分別表示該單元和其相鄰單元在該邊界處的值。本文所有計算都采用LLF格式數值通量:

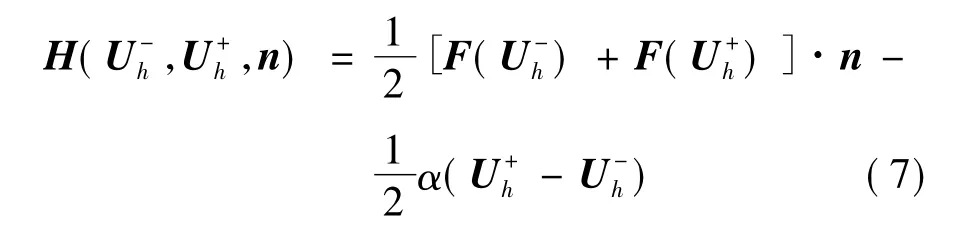
在物面和遠場分別采用無穿透和無反射邊界條件。式(6)最終的離散形式可寫為:

其中，M是質量矩陣，如果間斷有限元采用正交基函數，則是對角矩陣;R(u)是殘值;u包含Uh中所有的未知系數。對式(8)的求解采用牛頓-塊高斯賽德爾方法求解［18］。

2 人工粘性

人工粘性法［18］的思想就是在原Euler方程中加入一個耗散修正項，從而抑制激波附近的非物理振蕩。方程(1)變為如下形式:

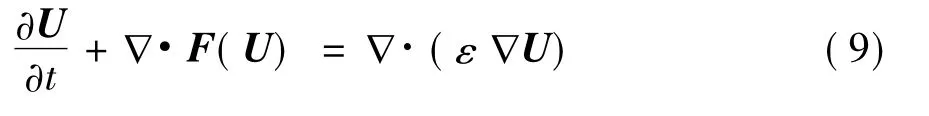
式(9)中，參數ε控制粘性項的大小。

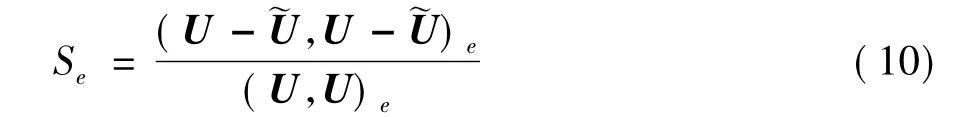
式中，(·，·)e表示L2(Ωe)空間的標準內積。這里預估Se的值能達到1/p4數量級。

單元的光順指示器確定后，粘性項系數通過以下函數定義:

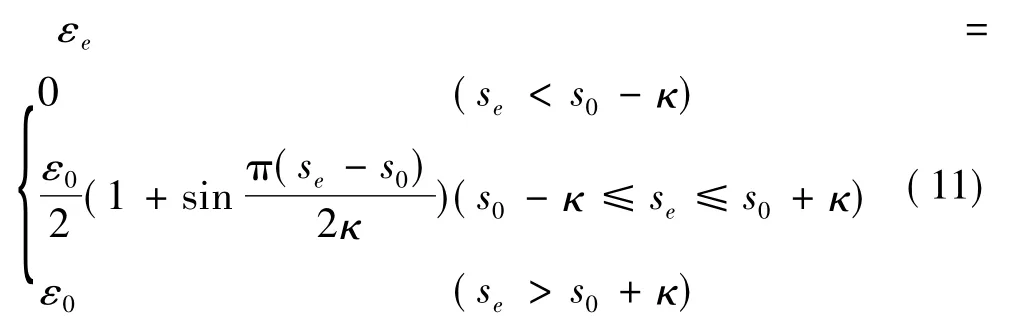
式(11)中，se= log10Se，參數 ε0= De/p，s0= log10(1/p4)，κ是人為定義常數。其中，De是計算元單元e的特征尺度。

由式(10)和式(11)可以看出，se是由U中高階項決定，表征了U的高階項的貢獻大小。解的光順程度越差se越大。εe只是作為se的分段函數，在數值表征上意義相同，它抹平光順區域的較小的se，突出非光順區域，使計算和表達更簡便。

3 網格自適應

3.1 網格加密

在計算過程中單元的ε達到設定好的上限閥值則認為該單元需要進行加密，采用三角形單元四分法對網格單元進行加密，如圖1所示。

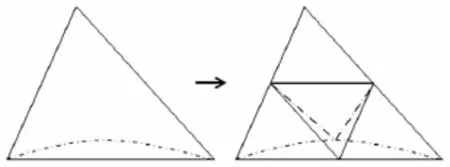
圖1 單元加密Fig.1 Element refinement

圖中實線單元為非物面單元，可以直接取三條邊的中點連線剖分加密。

Bassi指出高階間斷有限元對于物面形的表達精度十分敏感［3］，因而本文中的物面單元的物面邊均采用高階曲線逼近真實物面:在計算過程中設計物面邊

的高階曲線(本文中為6階)，即使網格十分稀疏，構造好的物面曲邊依然可以十分精確的表達真實物面，如圖1中左圖虛線所示。

在物面單元需要進行剖分時，利用已構造好的高階曲線找到逼近真實物面的物面邊的中點，然后連接另外兩條邊的中點生成四個新的網格單元，并且新生成的兩個物面單元的物面邊也用高階曲線擬合，如圖1中右圖虛線所示。

網格加密需要遵守以下原則:

1)相鄰單元的被剖分次數相差最多為1。

2)當單元的幾何尺寸細化到設定好的閥值之后就不可繼續剖分。

3.2 網格稀疏

在計算過程中，部分單元被加密后可能在進一步的迭代過程中解變得十分光滑，需要對其進行粗化以減少網格量。當加密過的單元的四個子單元ε均達到設定好的下限閥值時，則這四個子單元進行合并。如圖2所示。

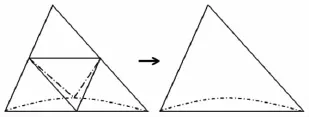
圖2 單元的粗化Fig.2 Element coarsening

圖2中，實線表示非物面單元的合并過程。若粗化后的單元為物面單元，物面邊依舊采用高階曲線逼近真實物面，如圖中虛線所示。

網格粗化是網格加密的逆向操作，需要遵守以下原則:

1)初始單元不可被粗化。

2)只有被加密過的單元才可以被粗化。

3)當鄰單元已經比判斷需要粗化的四個單元剖分次數大1時，不可進行粗化。

3.3 網格數據結構

為使程序的可移植性更高，將網格自適應作為模塊進行操作。雖然二叉樹結構存儲加密和粗化網格直觀高效，但自適應過程中增加與減少的點和線編號復雜且對于程序的結構不利。因而本文所有單元、點、線的存儲結構均為鏈表結構，加密過程中單元的增加操作如圖3所示。

E表示需要加密的單元，生成的四個子單元中間單元依舊為編號E，其余三個則排在總單元后三個，點與邊的操作類似。在這種操作下，網格模塊與程序流場計算模塊的接口不受自適應操作的影響，從而提高程序的可移植性。

同樣的，網格稀疏的過程單元減少過程如圖4所示。

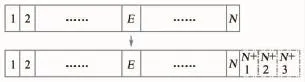
圖3 單元增加Fig.3 Elements increase

圖4 單元減少Fig.4 Elements decrease

其中E和三個fi表示由加密操作生成的四個子單元，合并后生成的單元依舊編號為E，而fi后的單元編號依次減3。

在網格加密過程中，每個子單元均設置兩個標記，用于記錄所在的初始單元號和本身的加密次數。在后續的網格稀疏過程中，根據這兩個信息和單元相鄰關系進行單元合并。

3.4 數據傳遞

網格加密和粗化的過程中，使各物理量在子單元內的積分值等于合并單元內的積分值，從而保證物理量的守恒。假設合并單元為E，各子單元為ei，uE(x，y)為合并單元的守恒變量的函數，uei(x，y)為子單元守恒變量的函數，則需滿足以下方程:

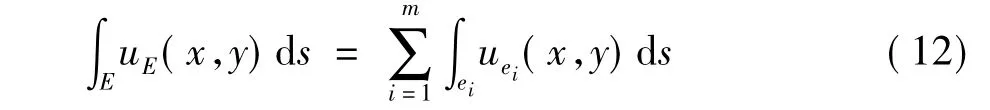
其中m為合并單元剖分后的子單元個數。

4 數值結果

4.1 圓柱繞流測試算例

為驗證物面構造與網格自適應結合的效果，本文首先對圓柱繞流(Ma=0.38、α=0)這一經典算例進行了數值模擬。

前人［3，8］做圓柱繞流計算為獲得精度較高的結果，網格均人為設計為規則分布。本文為驗證物面構造和自適應間斷有限元的優點，初始網格使用了分布較隨意、單元尺寸較極端的計算網格。

圖5給出了圓柱繞流網格，該網格共有80個單元，物面僅有8個點。

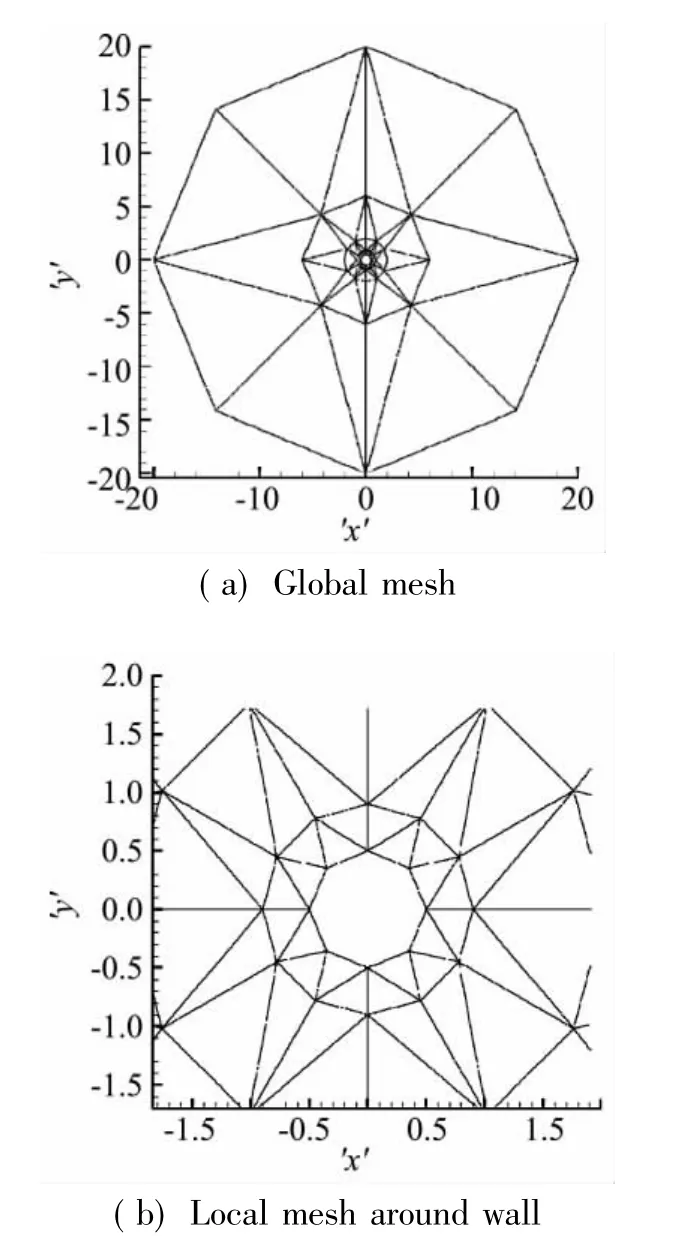
圖5 圓柱繞流計算網格Fig.5 Mesh around a circle

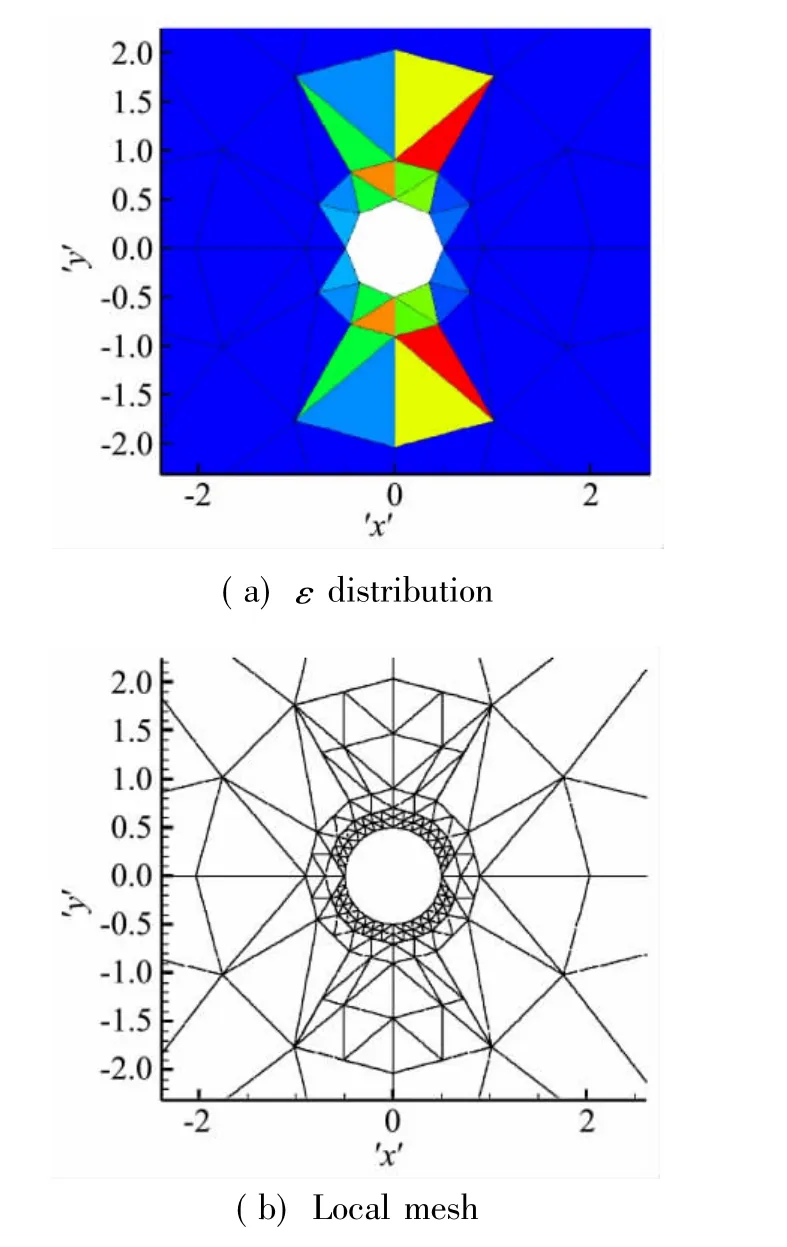
圖6 ε分布和自適應后的網格Fig.6 ε distribution and mesh after three times adaption

圖6(a)為在原始網格上p=4時ε分布，可以看出主要分布在流場數值可能出現數值解變化比較劇烈的區域。對這一區域進行網格自適應，2次自適應后的網格如圖6(b)所示。可以看出網格主要在ε集中區域自適應，從而僅需對這一區域的少量網格進行自適應操作。自適應前后的網格對比，發現自適應操作確實基于真實物面曲線，自適應后的網格更加逼近真實物面。

圖7給出了p=4情況下的圓柱繞流等馬赫線圖和壓強系數分布，可以看出壓強系數分布光滑并且對稱。

圖7 圓柱繞流等馬赫線圖和Cp分布Fig.7 Mach isolines and Cpdistribution

4.2 跨聲速NACA0012翼型繞流

采用上述自適應間斷有限元法給出了經典算例跨聲速(Ma=0.8、α=1.25)下NACA0012翼型繞流的數值結果。

圖8給出的NACA0012翼型的網格共有448個單元，而物面單元只有32個。

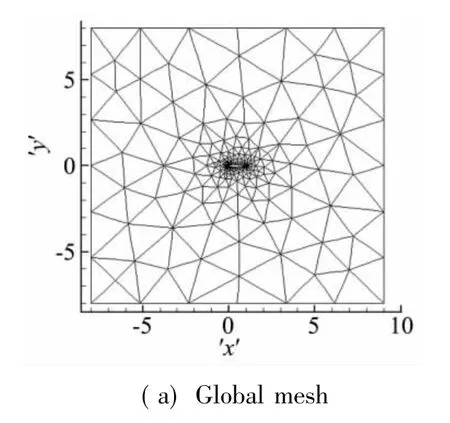
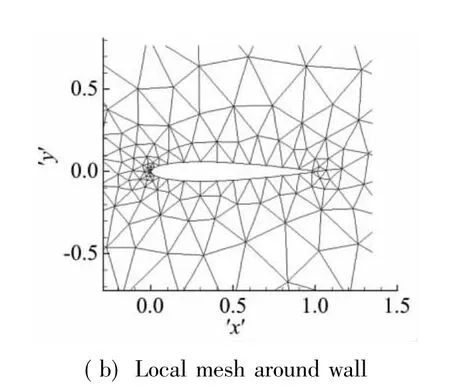
圖8 NACA0012翼型計算網格Fig.8 Mesh around NACA0012 airfoil

圖9給出了引入人工粘性未加入網格自適應的粘性項系數ε的分布與馬赫云圖。

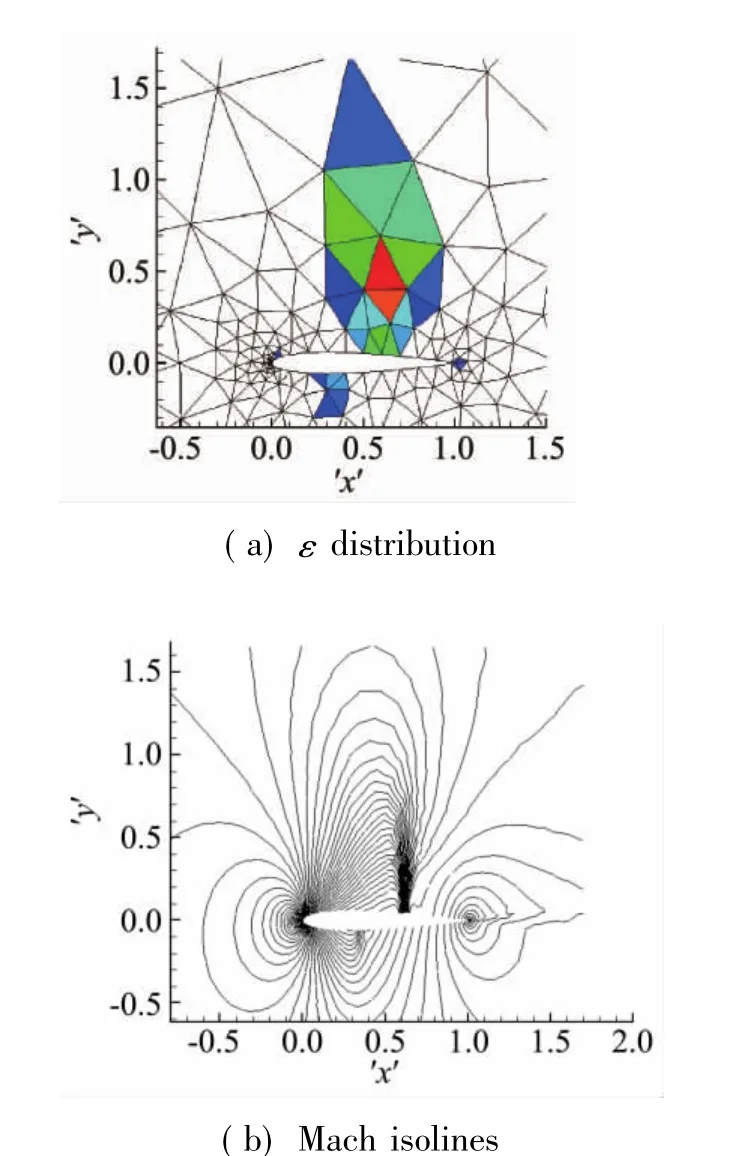
圖9 未加自適應的ε分布及等馬赫線圖Fig.9 ε distribution and Mach isolines without adaption

從圖中可以看出雖然網格十分稀疏，但依然可以在一個網格尺度內捕捉到激波，并且ε的分布集中在激波區域。

圖10給出了1次、2次自適應后的網格變化。圖11給出了網格自適應過程中局部網格的細化和粗化的動態變化情況。

從圖中可以看出，自適應過程中激波區域的網格加密，而遠離激波區域在精度低的時候加密了的單元則合并降低網格量。

圖12給出了自適應結束時的網格分布和ε分布。

圖13給出了添加自適應后的五階精度(p=4)的等馬赫線圖和表面壓強系數分布。

圖10 1次和2次自適應后的網格Fig.10 Mesh after once and twice adaption

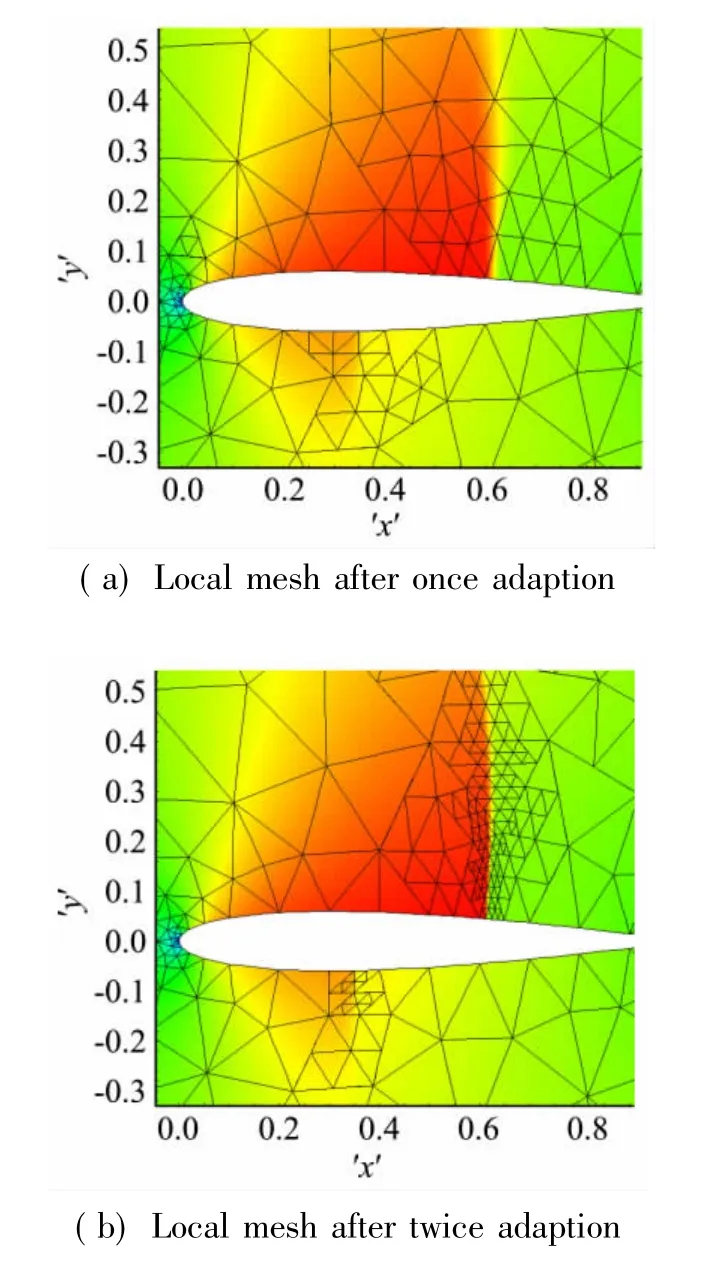
圖11 1次和2次自適應后的局部網格Fig.11 Local mesh after once and twice adaption

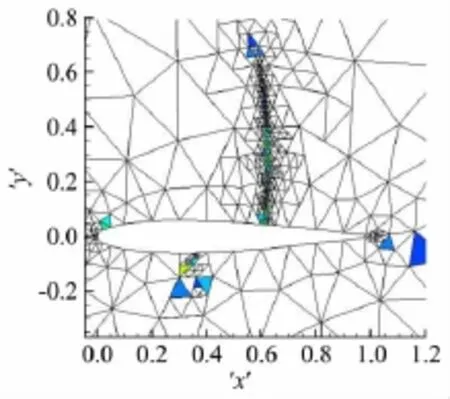
圖12 自適應結束的網格和ε分布Fig.12 Mesh and ε distribution after adaption

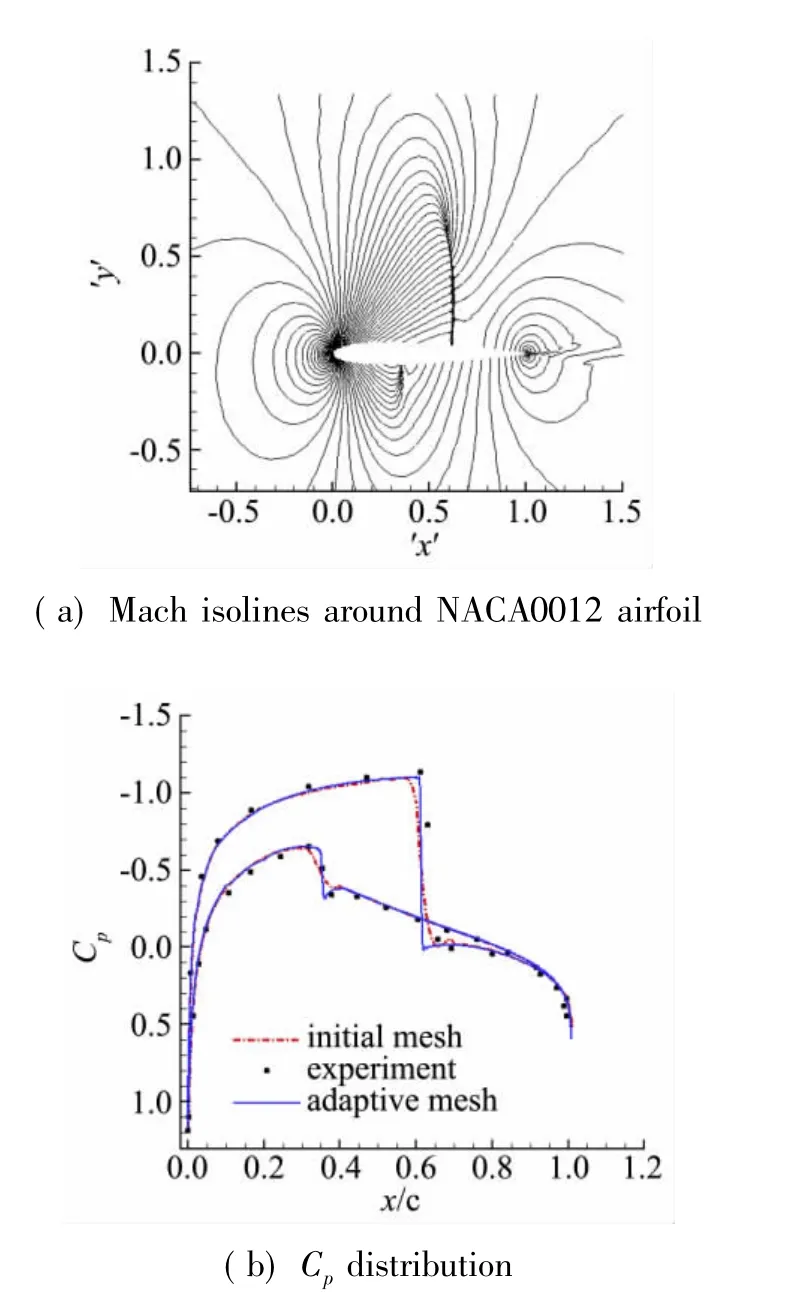
圖13 等馬赫線圖和Cp分布曲線Fig.13 Mach isolines and Cpdistribution

從圖中可以看出，自適應后的數值結果較原始網格上的數值精度有顯著提高，并且激波捕捉更精確接近實驗值。

4.3 超聲速NACA0012翼型繞流

為驗證方法的適應性，采用上述自適應間斷有限元法給出了超聲速(Ma=5.0、α=0)下NACA0012翼型繞流的數值結果(p=4)。

初始網格如圖14，初始網格數為660。自適應計算結束后的馬赫云圖及網格、ε分布如圖15所示。

從圖中可以看出，自適應操作主要集中在頭部激波區域。

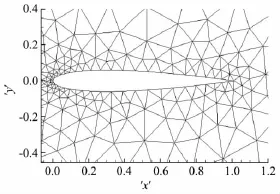
圖14 局部網格Fig.14 Local mesh

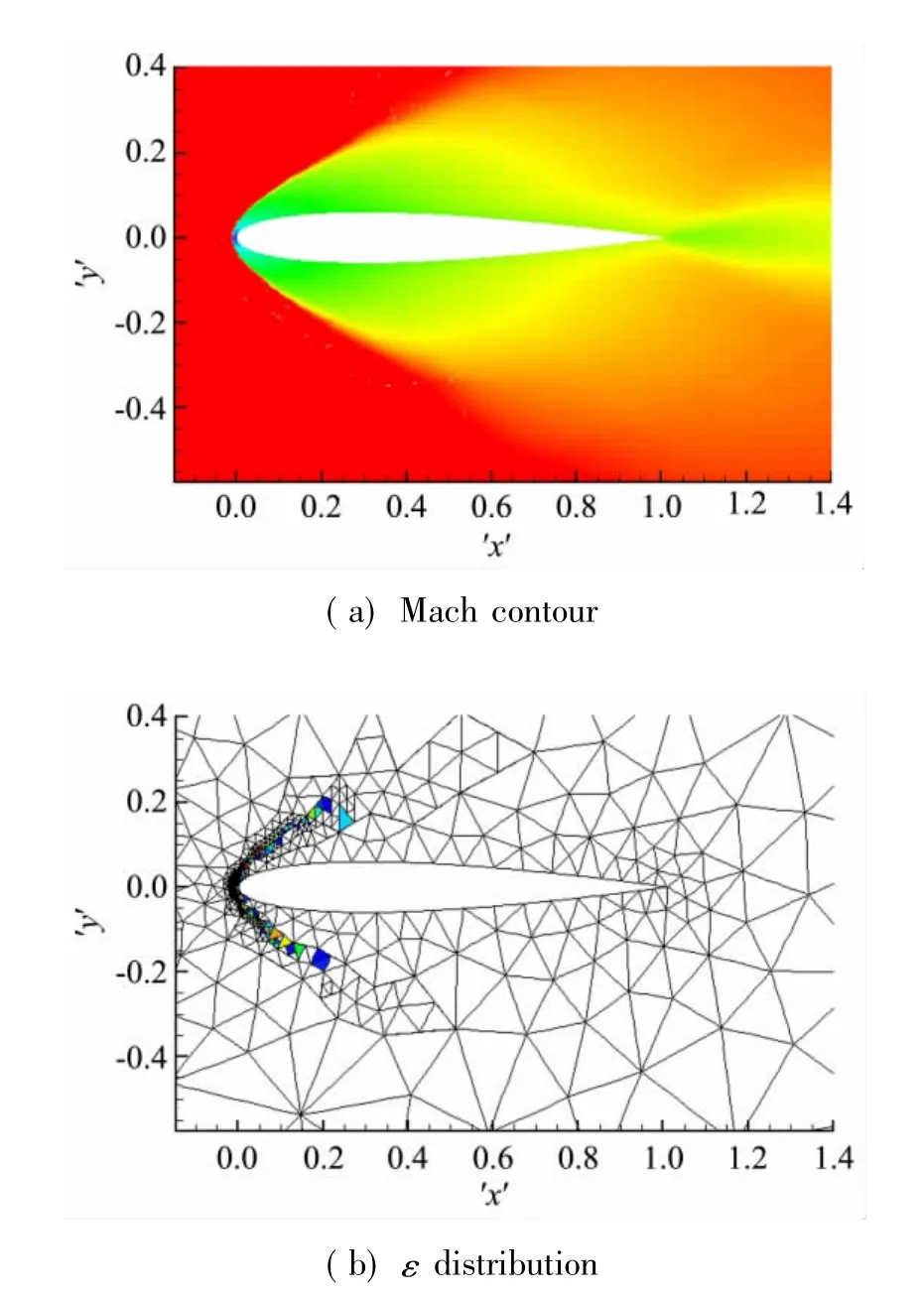
圖15 馬赫云圖及ε分布Fig.15 Mach contour and ε distribution

5 結論

(1)將數值解的高階項貢獻量化后作為自適應指示器可行并直觀有效。

(2)即使在很稀疏的初始網格基礎上，使用基于真實物面逼近的網格自適應方法也可以獲得高精度的數值解。

(3)本文設計的自適應方法提高了數值解精度的同時有效地控制了網格量。

對于非定常問題和三維問題，自適應方法在節省網格工作量和提高計算效率方面作用更為突出。同時具有加密和粗化的功能在非定常計算中會得到更有意義的應用，該部分研究正在進行中。在粘性流動的情況下可以在不引入人工粘性項的前提下計算人工粘性項系數，將其作為網格自適應判據，這部分工作也正在進行。

［1］ Reed W H，Hill T R.Triangular mesh methods for the neutron transport［R］.Los Alamos Scientific Laboratory Report LA-UR-73-479，1973.

［2］ Bassi F，Rebay S.A high-order accurate discontinuous finite element method for the numerical solution of the compressible Navier-Stokes equations［J］.Journal of Computational Physics，1997，131 (2):267-279.

［3］ Bassi F，Rebay S.High-order accurate discontinuous finite element solution of the 2D Euler equations［J］.Journal of Computational Physics，1997，138(2):251-285.

［4］ Cockburn B，Shu C.The Runge-Kutta discontinuous Galerkin method for conservation laws V:multidimensional systems［J］.Journal of Computational Physics，1998，141(2):199-224.

［5］ Cockburn B，Shu C.The local discontinuous Galerkin method for time-dependent convection-diffusion systems［J］.SIAM Journal on Numerical Analysis，1998，35(6):2440-2463.

［6］ Nguyen N C，Persson P O，Peraire J.RANS solutions using high order discontinuous Galerkin methods［R］.AIAA 2007-0914.

［7］ Lu Hongqiang，Wu Yizhao，Zhou Chunhua，et al.High resolution of subsonic flows on coarse grids［J］.Acta Aeronautica et Astronautica Sinica，2009，30(2):200-204.(in Chinese).

呂宏強，伍貽兆，周春華，等.稀疏非結構網格上的亞音速流高精度數值模擬［J］.航空學報，2009，30(2):200-204.

［8］ Lu Hongqiang，Zhu Guoxiang，Song Jiangyong，et al.High-order discontinuous Galerkin solution of linearized Euler equations［J］.Chinese Journal of Theoretical and Applied Mechanics，2011，43 (3):621-624.(in Chinese).

呂宏強，朱國祥，宋江勇，等.線化歐拉方程的高階間斷有限元數值解法研究［J］.力學學報，2011，43(3):621-624.

［9］ Lu H.High-order discontinuous Galerkin solution of low-Re viscous flows［J］.Modern Physics Letters B，2009，23(03):309-312.

［10］Zhang Laiping，Liu Wei，He Lixin，et al.A class of discontinuous Galerkin/finite volume hybrid schemes based on the“static re-construction”and“dynamic re-construction”［J］.Chinese Journal of Theoretical and Applied Mechanics，2010，42(6):1013-1022.(in Chinese).

張來平，劉偉，賀立新，等.基于靜動態混合重構的DG/FV混合格式［J］.力學學報，2010，42(6):1013-1022.

［11］Yu J，Yan C.An artificial diffusivity discontinuous Galerkin scheme for discontinuous flows［J］.Computers＆Fluids，2013，75(20): 56-71.

［12］Yu Jian，Yan Chao.Study on discontinuous Galerkin method for navier-stokes equations［J］.Chinese Journal of Theoretical and Applied Mechanics，2010，42(5):962-969.(in Chinese).

于劍，閻超.Navier-Stokes方程間斷Galerkin有限元方法研究［J］.力學學報，2010，42(5):962-969.

［13］Yang X，James A J，Lowengrub J，et al.An adaptive coupled levelset/volume-of-fluid interface capturing method for unstructured triangular grids［J］.Journal of Computational Physics，2006，217 (2):364-394.

［14］Remacle J F，Li X，Shephard M S，et al.Anisotropic adaptive simulation of transient flows using discontinuous Galerkin methods［J］.International Journal for Numerical Methods in Engineering，2005，62(7):899-923.

［15］Xu Yun，Yu Xijun.Adaptive discontinuous Galerkin methods for hyperbolic conservation laws［J］.Chinese Journal of Computational Physics，2009，26(2):159-168.(in Chinese).

徐云，蔚喜軍.自適應間斷有限元方法求解雙曲守恒律方程［J］.計算物理，2009，26(2):159-168.

［16］Wu Di，Yu Xijun.Adaptive discontinuous Galerkin method for euler equations［J］.Chinese Journal of Computational Physics，2010，27 (004):492-500(in Chinese).

吳迪，蔚喜軍.自適應間斷有限元方法求解三維歐拉方程［J］.計算物理，2010，27(004):492-500.

［17］VonNeumann J，Richtmyer R D.A method for the numerical calculation of hydrodynamic shocks［J］.Journal of Applied Physics，1950，21(3):232-237.

［18］Xia Y D，Wu Y Z，Lv H Q，et al.Parallel computation of a highorder discontinuous Galerkin method on unstructured grids［J］.Acta Aerodynamica Sinica，2011，29(5):537-541.(in Chinese).

夏軼棟，伍貽兆，呂宏強，等.高階間斷有限元法的并行計算研究［J］.空氣動力學學報，2011，29(5):537-541.

［19］Lu H，Berzins M，Goodyer C E，et al.Adaptive high-order discontinuous Galerkin solution of elastohydrodynamic lubrication point contact problems［J］.Advances in Engineering Software，2012，45 (1):313-324.

Adaptive discontinuous Galerkin method to solve Euler equations based on high-order approximative boundary

Sun Qiang，Lu Hongqiang*，Wu Yizhao
(College of Aerospace Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China)

A high-order discontinuous method(DGM)is integrated with adaptive method to solve Euler equations on unstructured mesh.Contribution of the polynomial’s highest-order terms is quantified in the form of artificial viscous coefficient.The coefficient is regarded as the indicator of h-adaptivity.Elements where the coefficients are greater than the upper limit are refined.Those where the coefficients are less than the lower limit are coarsened if they have been refined.A high-order geometric approximation of curved boundaries is adopted to ensure the convergence.Numerical results of test cases are consistent with corresponding experimental ones.High accurate numerical results can be obtained with the h-adaptive method at low expense.

high-order DGM;adaptive method;Euler equations;artificial viscosity;high-order boundary approximation

V211.3

Adoi:10.7638/kqdlxxb-2014.0027

0258-1825(2015)04-0446-08

2014-04-23;

2014-07-08

國家自然科學基金(11272152);航空科學基金(20101552018);江蘇高校優勢學科建設工程資助項目

孫強(1987-)，男，山東萊陽市人，博士研究生，研究方向:計算流體力學.E-mail:submarineultra@126.com

呂宏強*(1977-)，男，博士，副教授，E-mail:hongqiang.lu@nuaa.edu.cn

孫強，呂宏強，伍貽兆.基于高階物面近似的自適應間斷有限元法歐拉方程數值模擬［J］.空氣動力學學報，2015，33(4):446-453.

10.7638/kqdlxxb-2014.0027 Sun Q，Lu H Q，Wu Y Z.Adaptive discontinuous Galerkin method to solve Euler equations based on high-order approximative boundary［J］.Acta Aerodynamica Sinica，2015，33(4):446-453.