PSE方法研究平板邊界層中三波共振的非線性作用機制

張 麗

(天津大學力學系，天津 300072)

PSE方法研究平板邊界層中三波共振的非線性作用機制

張 麗*

(天津大學力學系，天津 300072)

用拋物化穩定性方程(PSE)方法數值模擬了實驗中三波共振中三維擾動的非線性作用情況，得到的計算結果與實驗數據在定量上比較相符。研究表明擾動演化的定性行為與理論描述的結果是一致的，即二維波在初始階段和參數共振階段按照線性指數增長，三維波在初始階段同樣按照線性指數增長。在非線性作用比較強時，三維波快速增長起來，最終作用在二維波上，使其再次增長起來，從而引起轉捩。

三波共振;PSE方法;參數共振;非線性作用;轉捩

0 引言

不可壓縮邊界層轉捩的實驗研究發現當二維擾動的幅值增長到一定階段時，在下游會觀察到三維擾動的產生，并且三維擾動的增長率要遠大于其線性理論預測的增長率。1962年Klebanoff［1］等人對平板邊界層的非線性擾動演化及轉捩問題進行了系統研究，發現了其流向的Λ渦結構如圖1(a)所示的K型三維擾動。Saric［2］等人在 1984年用煙線實驗研究了轉捩中快速增長的三維擾動，在下游觀察到如圖1(b)所示的交錯的Λ渦結構，即C型和H型擾動。

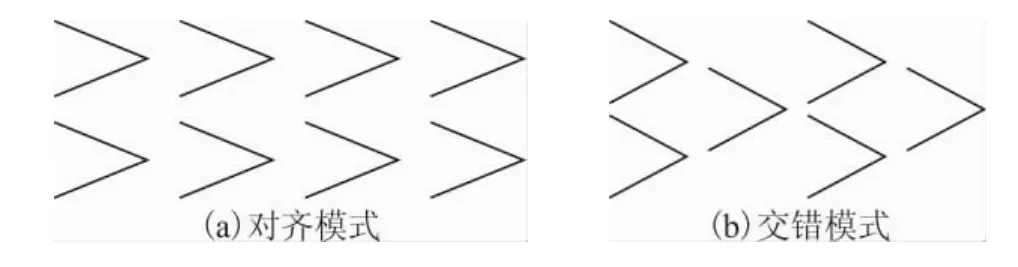
圖1 煙線演化示意圖Fig.1 The smoke line evolution

Kachanov和Levchenko［3］通過實驗研究發現在不可壓縮平板邊界層中，如果加入的二維波的初始幅值很小，就會出現C型轉捩，當幅值稍微增大時，將會出現H型轉捩，當幅值更大時，就會出現K型轉捩。在Kachanov實驗的基礎上Corke和Mangano［4］用熱線感應的實驗方法對擾動的初始幅值更小的C型和H型轉捩問題，并考慮了二維與三維擾動的相位角，結果發現，增大二維擾動的初始幅值會使轉捩提前發生，并且不同的相位角會影響三維擾動的增長速度。Zelman［5］和 Sayadi［6］等用數值模擬的方法對Kachanov實驗進行分析，得到了與實驗數據定性上相符的結果。在Kachanov實驗的啟發下，董亞妮和周恒［7］用直接數值模擬的方法驗證了可壓縮流體中二次失穩和三波共振機制的存在。三波共振的理論研究方面，Herbert［8-9］用二次失穩理論，對三波共振中參數共振階段做了詳細的解釋。Mankbadi［10］等考慮了臨界層中擾動的非線性作用這一方面來對參數共振階段進行了分析，并說明二維平面波在參數共振階段一直遵循著線性指數增長。Mankbadi，Wu＆Lee［11］和Wu［12］用三層結構理論研究了Blasius邊界層中上支界擾動的三波共振情況，他們發現非線性作用主要發生在臨界層以及附近的‘擴散層’中，臨界層處的非線性作用以及粘性決定著擾動的發展。

本文將研究三波共振中三維擾動在邊界層中的非線性作用情況，觀察了三維擾動及由于非線性作用產生的其他高次諧波的擾動演化情況，并與實驗結果進行了對比。我們采用了一種比較方便的PSE方法來研究上述問題，該方法相對于eN方法需要較多的計算，但是相比與直接數值模擬方法(DNS)節省很多的計算量，同時還可以考慮流動的非平行性，解決擾動的非線性演化過程，與現實中擾動的演化情況相比是比較符合的。并且我們采用了一種新的求解流向波數α的方法，不用再對α進行迭代求解，節省了計算時間和計算量。因此本文用改進后的PSE方法來研究邊界層中擾動的演化過程，分析三維擾動在Blasius邊界層中的非線性作用。

1 控制方程和數值方法

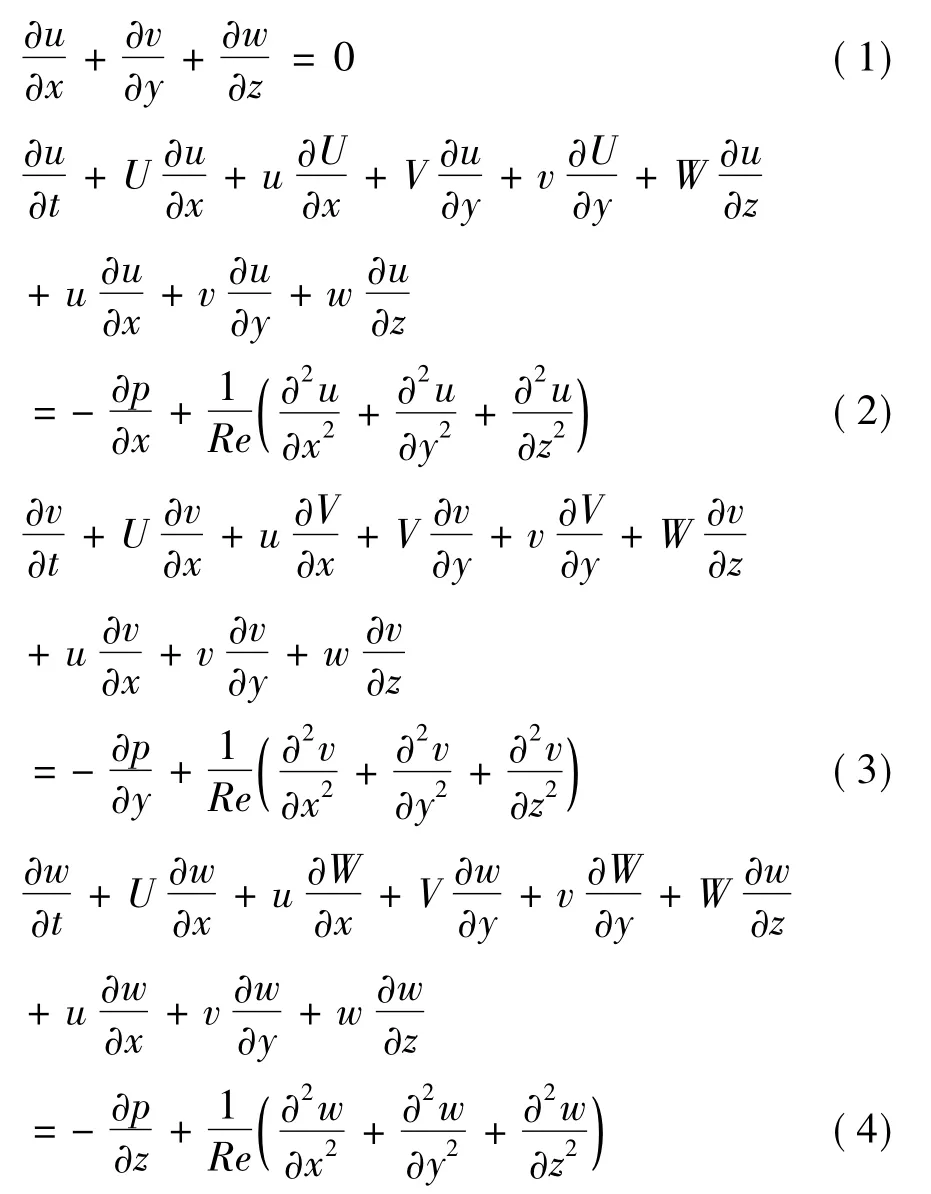
假設擾動是時間和展向的周期函數，擾動表示為:

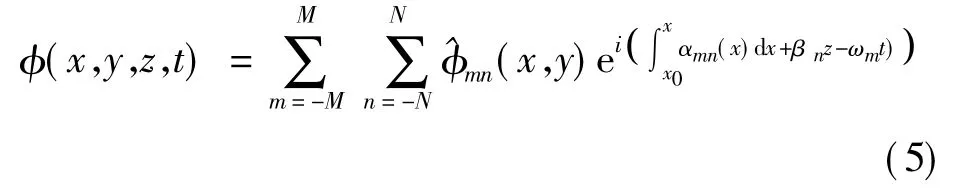
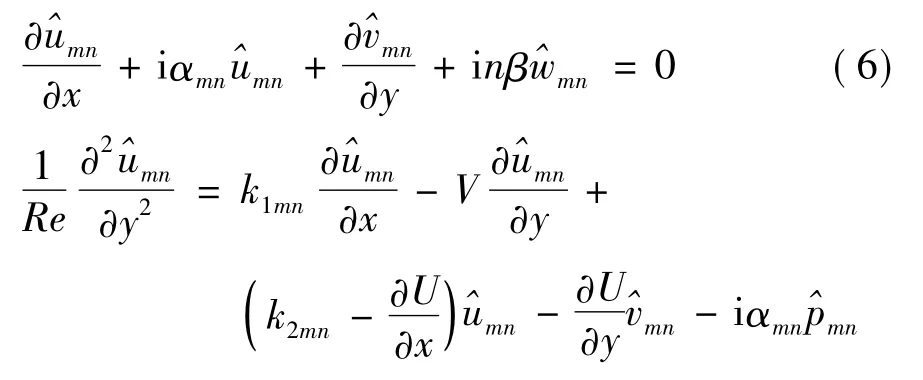
將PSE方程寫成算子的形式:

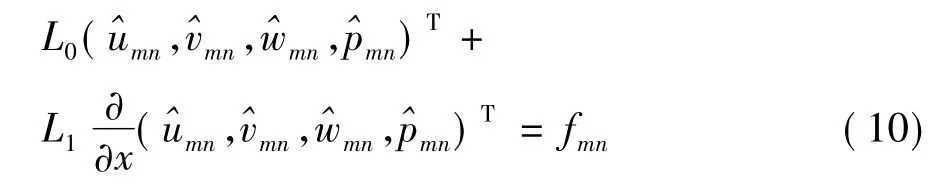
式中fmn表示非線性項。

求解PSE方程最關鍵的是如何確定流向波數α，通長采用的方法是選取下列四個補充條件的其中之一:

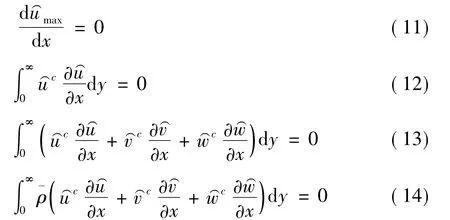
式中上標c表示復共軛，這些條件都是以基本擾動的形狀沿流向不變，或者動能沿流向不變為前提的。對于線性PSE，在擾動幅值比較小并且邊界層沿流向的變化不太快時，上述前提條件是可以滿足的。但是在非線性PSE中，如果擾動的幅值比較大，非線性作用開始體現出來時，基本擾動會有較大的變形;另一方面，在邊界層沿流向變化比較快時，即使是線性PSE，基本擾動的變形也會比較快，所以上述補充條件的前提就不成立了。除此之外，使用以上補充條件時，需要對基本波數α進行迭代求解，計算時間很長并且計算量比較大。

依據流動穩定性理論，我們建議了一種新的求解流向波數α的補充條件，即對某個流向位置利用:

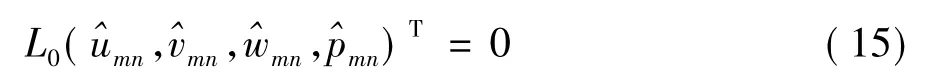
來確定當地位置處的流向波數αmn，再由非線性拋物化穩定性方程計算擾動向下游的演化。我們這樣處理的原因是，線性算子L0反應了當地平行流假設下擾動波特性，而當地基本波數αmn應該滿足當地平行流假設下擾動波的特性，因此由L0來確定αmn。

本文采用的基本流是二維平板Blasius相似性解入口條件。流向x方向上采用Karniadakis等［14］建議的顯隱結合的三階計算格式進行離散，法向y方向我們采用Malik［15］差分格式，有四階精度并且可以適用于變間距網格。流向方向網格選取等間距網格，為了保證壁面邊界層內的網格點數足夠多，法向y方向上選取變間距網格。

2 數值結果

首先針對Kachanov和Levchenko［3］的實驗，參考其擾動參數(x*=600mm，雷諾數046，邊界層排移厚度，選取計算域入口的擾動為一個二維波和一對三維波。

表1 入口處擾動參數Table 1 The perturbation parameters of the entrance

依據實驗中測量的擾動演化曲線，我們提取了二維擾動的初始幅值A2D，rms=5×10-3、三維波初始幅值A3D，rms=3×10-5，并用PSE方法計算了的擾動演化情況，同時與實驗結果進行了對比。實驗中法向測量點固定在y*/δ*=0.26位置處，其中δ*是當地邊界層名義厚度。

圖2中，線條是數值結果，符號是實驗結果。二維波幅值在初始階段按照線性指數增長，當穿出中性曲線的中性點(αi=0)時，幅值開始衰減;由于初始階段幾乎沒有非線性作用，三維波的幅值會經歷一段線性演化，隨后由于二維波幅值的增長，二維、三維波之間的三波共振使得三維波快速增長，但二維波在相當一段距離內仍保持自身的線性增長，因此它起著“催化劑”作用;在最后階段，二維波受到三維波的反作用幅值會再次增長起來。我們可以看出二維波幅值PSE與實驗結果相比很符合。由于三維波的初始幅值很小，實驗中初始階段的三維波演化情況很難測出，所以這一階段的三維波幅值演化可以忽略掉。同時還可以觀察到下游三維波幅值的增長情況與實驗結果還是比較符合的。

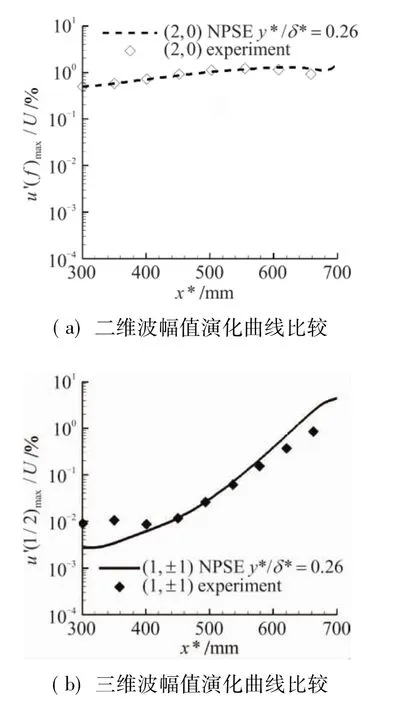
圖2 幅值演化曲線比較Fig.2 Compared of the amplitude evolution curve

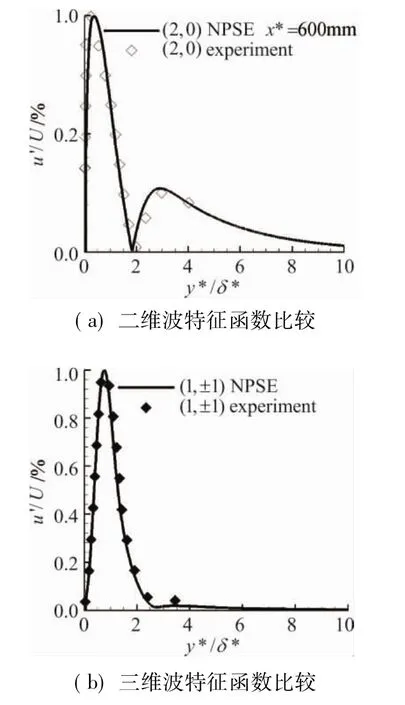
圖3 特征形狀函數比較Fig.3 Compared of the characteristic function

圖3顯示的是x*=600 mm處歸一化之后的擾動的特征形狀函數隨法向位置的分布，并與實驗數據進行了比較。歸一化之后的二維波和三維波特征形狀函數分布與實驗相比，符合的比較好。同時也說明了實驗中測量的擾動是T-S波。

由于非線性的作用，在擾動演化過程中會產生其他頻率的波，我們觀察了幾種比較特殊的擾動的幅值演化情況，并與實驗結果進行了對比，如圖4所示。

在流向比較靠前的位置處就會出現(4，0)波和(3，±1)波，并且其幅值隨著流向會快速的增長起來，其結果與實驗結果比較相符。(5，±1)在流向比較靠下游的地方出現，幅值增長比較小，與實驗結果比較趨勢相同，數值上有所偏差。由于(6，0)的幅值很小，實驗中測量時有一定的困難，因此，PSE結果與實驗結果近似平行，數值上有一定的差距。因為受到實驗環境、實驗技術、實驗條件的影響，實驗數據或多或少與數值模擬結果有所不同，但總體定性上、定量上還是比較符合的。

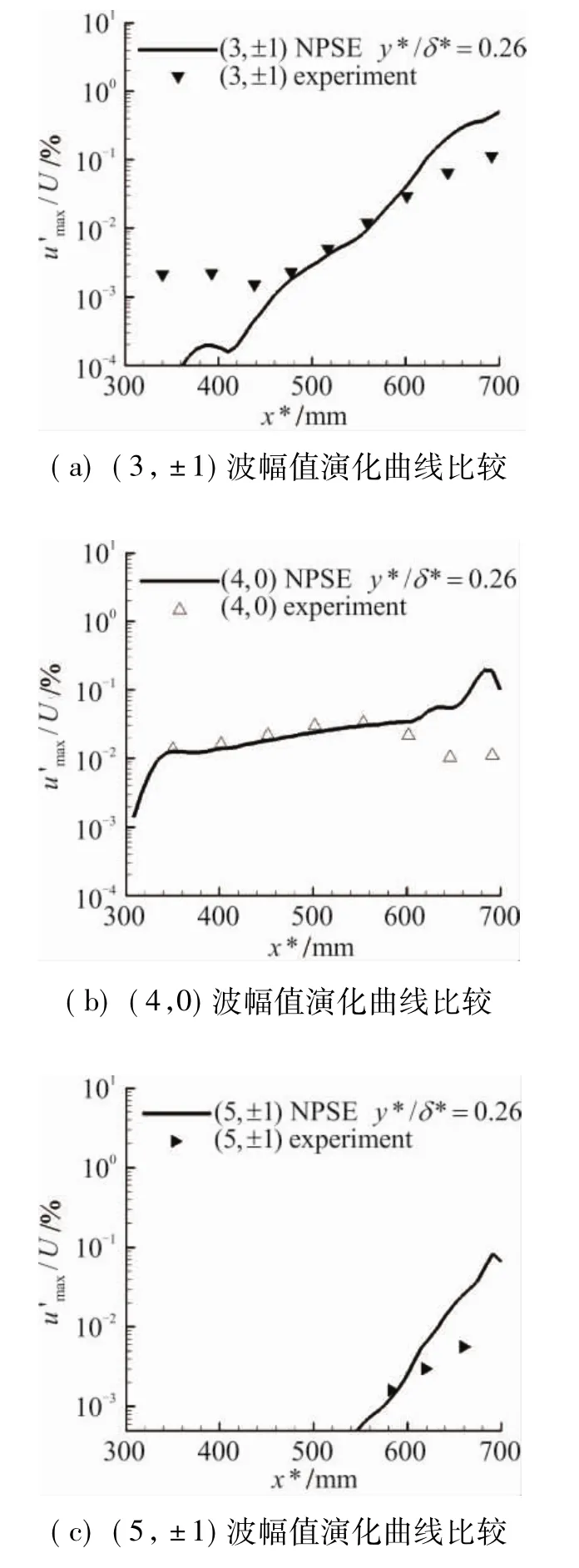
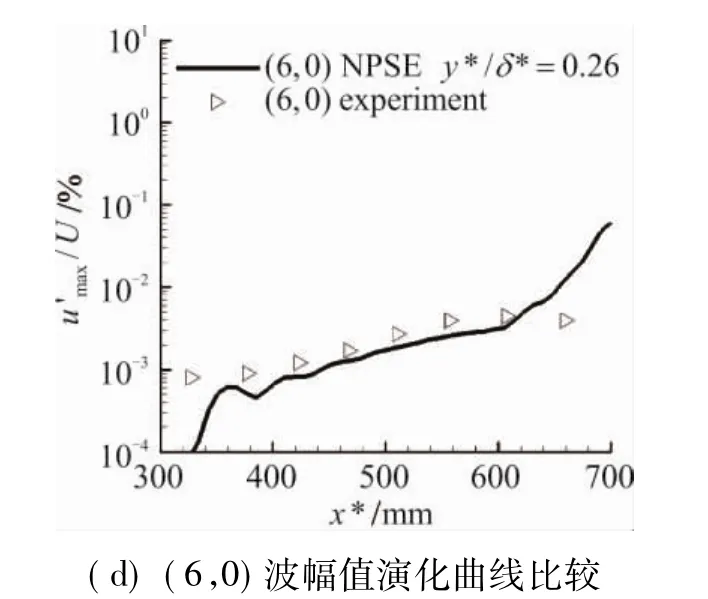
圖4 高階擾動幅值演化曲線比較Fig.4 Compared of high-order disturbance evolution curve

圖5給出了高次諧波歸一化之后的特征形狀函數分布情況，并將其與實驗中的數據進行了比較。其中菱形符號表示實驗結果，實線是PSE數值結果。x*=600 mm位置處擾動已經快速的增長起來，此時的非線性作用已經很明顯，擾動的特征形狀函數會有所變形。考慮到(3，±1)波和(5，±1)波的幅值都比較小，測量中會存在一定的困難，PSE計算結果與實驗結果相比較，還是比較符合的。

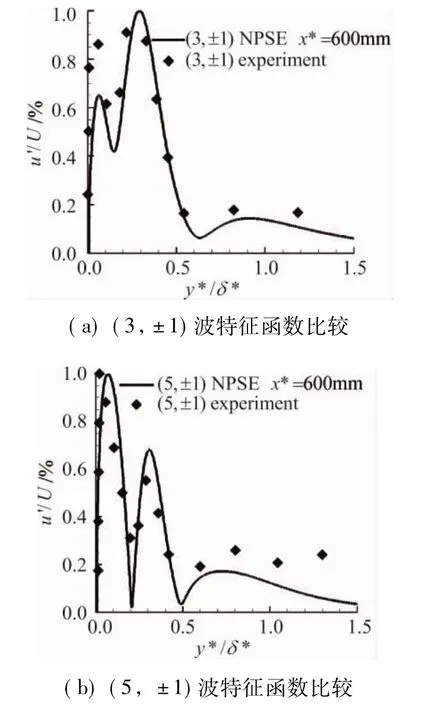
圖5 高階擾動特征形狀函數比較Fig.5 Compared of the high-order disturbance characteristic function

3 結論

同樣按照線性指數增長。在非線性作用比較強時，三維波快速增長起來，并給二維波一個反作用使得二維波再次增長起來，這與理論描述的結果是一致的。從而證實了三維擾動的非線性作用機制。

［1］ Klebanoff P S，Tidstrom K D，Sargent L M.The three-dimensional nature of boundary-layer instability［J］.J.Fluid Mech.，1962，12:1-34.

［2］ Saric W S，Thomas A S W.Experiments on the subharmonic route to turbulence in boundary layers［J］.Turbulence and Chaotic Phenomena in Fluids，1984:117-122.

［3］ Kachanov，Yu S，Levchenko V Ya.The resonant interaction of disturbances at laminar-turbulent transition in a boundary layer［J］.J.Fluid Mech.，1984，138:209-247.

［4］ Corke T C，Mangano R A.Resonant growth of three-dimensional modes in transitioning Blasius boundary layers［J］.J.Fluid Mech.，1989，209:93-150.

［5］ Zelman M B，Maslennikova I I.Tollmien-Schlichting-wave resonant mechanism for subharmonic-type transition［J］.J.Fluid Mech.，1993，252:449-478.

［6］ Sayadi T，Hamman C W，Moin P.Direct numerical simulation of complete H-type and K-type transitions with implications for the dynamics of turbulent boundary layers［J］.J.Fluid Mech.，2013，724:480-509.

［7］ DongYani.A numerical study for the resonant triad interaction and secondary instability in a three-dimensional supersonic boundary layer［D］.［Master’s Thesis］.Tianjin:Tianjin University，2005.(in Chinese)

董亞妮.三維超音速邊界層中三波共振和二次失穩機制的數值模擬研究［D］.［碩士學位論文］.天津:天津大學，2005.

［8］ Herbert T.Subharmonic three-dimensional disturbances in unstable plane shear flows［R］.AIAA-83-1759，1983.

［9］ Herbert T.Secondary instability of boundary layers［J］.Ann.Rev.Fluid Mech.，1988，20:487-526.

［10］Mankbadi R R.Critical-layer nonlinearity in the resonance growth of three-dimensional waves in boundary layer［R］.1990，NASA TM-103639.

［11］Mankbadi R R，Wu X，Lee S S.A critical-layer analysis of the resonant-triad in boundary-layer transition:nonlinear interactions［J］.J.Fluid Mech.，1993，256:85-106.

［12］Wu X.On critical-layer and diffusion-layer nonlinearity in the threedimensional stage of boundary-layer transition［J］.Proc.R.Soc.Lond.，1993，A433:95.

［13］Li Jia.The numerical simulation of transition for spanwise wavepacket disturbances in boundary layers and the prediction by the PSE methed［D］.［PhD Thesis］.Tianjin:Tianjin University，2012.(in Chinese)

李佳.邊界層中展向波包型擾動轉捩的數值模擬及用PSE方法轉捩預測［D］.［博士畢業論文］.天津:天津大學，2012.

［14］Karniadkis G E，Israeli M，Orszag S A.High-order splitting methods for the incompressible Navier-Stokes equations［J］.J.Comput.Phy.，1991，97:414-443.

［15］ Zhou Hen，Zhao Gengfu.Hydrodynamic Stability［M］.Beijing: National Defence Industry Press，2004.(in Chinese)

周恒，趙耕夫.流動穩定性［M］.北京:國防工業出版社，2004.

文章用PSE方法研究了三波共振中擾動的演化情況，研究表明實驗和PSE數值結果在定量上還是比較相符的。定性上的比較中，二維波在初始階段和參數共振階段按照線性指數增長，三維波在初始階段

The PSE approach to study the nonlinear evolution of three-dimensional disturbances in incompressible boundary layers on flat-plate

Zhang Li*
(School of Mechanical Engineering，Tianjin University，Tianjin 100072)

The study of the nonlinear evolution of three-dimensional disturbances in the boundary layers has a great theoretical research significance to the hydrodynamic stability.PSE method is adopted to study the subharmonic resonance in the experiment，and comparison between PSE results and experimental data is presented.The numerical results by PSE match the experiment results basically in quantitatively.In the qualitative comparison，the plane wave experiences a linear exponential growth in the beginning stage and parametric-resonance stage，and the subharmonic oblique waves also experience a linear exponential growth in the initial stage.However，when the nonlinear effects is relatively strong，the subharmonic oblique waves experience a super exponential growth that is faster than the exponential growth predicted by the linear theory，and stmulate the plane wave to make it increase again.This result is a consistent with the theoretical description.

subharmonic resonance;PSE approach;resonant-triad resonance;nonlinear evolution; transition

V211.3

A

10.7638/kqdlxxb-2014.0022

0258-1825(2015)04-0441-05

2014-04-14;

2014-05-26

張麗*(1990-)，女，碩士，流體力學專業.E-mail:likecrazy0701@sina.com

張麗.PSE方法研究平板邊界層中三波共振的非線性作用機制［J］.空氣動力學學報，2015，33(4):441-445.

10.7638/kqdlxxb-2014.0022 Zhang Li.The PSE approach to study the nonlinear evolution of three-dimensional disturbances in incompressible boundary layers on flat-plate［J］.Acta Aerodynamica Sinica，2015，33(4):441-445.