機構系統關節約束反力分析

敬 謙，劉宏昭，王庚祥

(1.西安理工大學 機械與精密儀器工程學院，西安 710048；2.隴東學院 機械工程學院，甘肅 慶陽 745000)

機構系統關節反力是約束反力的一種，關節反力計算的準確性對機構動力學分析、工作特性分析、結構設計、零部件選取以及機器工作壽命預測等意義重大。近年來，機構系統運動中如何引入拉格朗日乘子并明確其物理意義仍然是國內外研究的熱點[1]。關于拉格朗日乘子與關節反力的關系問題，丁光濤[2]從理論分析的角度討論了完整約束和非完整約束力學系統中引入待定乘子兩種不同的途徑，著重研究了變分原理條件極值中引入待定乘子修正系統的拉格朗日函數的方式，給出了拉格朗日乘子與理想約束反力之間的關系表達式。

關節反力常見的計算方法有牛頓歐拉方程、達朗貝爾原理以及拉格朗日方程。趙燕等[3]利用牛頓歐拉法列出所有構件的力和力矩平衡方程，確定了驅動力和平臺受到的約束反力，但同時也指出當機構結構復雜或需要求解的主動力和運動副反力的數目更多時，這種方法很不方便。Marek 等[4-5]討論了包含有冗余約束和奇異約束的剛體系統約束反力的求解方法，給出了在包含非獨立約束條件下能夠確定單一關節反力或一組關節反力的前提條件。通過整車系統動力學分析,劉剛同樣選用牛頓歐拉方程對工程機構鉸接系統鉸點動態約束反力進行了研究[6]。文獻[7]建立了多對均布傳力桿空間RCCR機構模型，利用達朗貝爾原理計算出了在動力條件下機構慣性力引起約束反力的理論表達式。拉格朗日增廣法將加速度約束方程與動力學方程耦合進行積分，求解時必須考慮速度和位移約束的違約修正,如果修正不當,往往會使得求解發散。為了避免違約修正，原亮明等[8]將完整約束方程進行泰勒展開后與動力學方程聯立求解并以一個七桿機構為例，驗證了算法的正確性。彭慧蓮等[9]以多體系統中的樹形結構為例，詳細介紹了選用局部坐標建立約束方程的方法和優點，指出對具有光滑固定面約束和光滑柱鉸鏈約束的平面多剛體系統的關節約束反力與Lagrange 乘子一一對應，并以曲柄滑塊機構為例利用矢量方程法加以驗證。上述文獻對拉格朗日增廣法中待定乘子的引入原理進行了詳細介紹，并從理論分析的角度詳述了機構系統在受完整約束或非完整約束下關節反力的數值計算方法。另外，當前利用增廣法求解機構系統動力學的目的主要集中在對機構運動特性的分析[10-12]，而對關節反力本身的物理含義及求解方法有效性問題研究較少，這對研究桿件壽命、關節磨損特性等問題形成一定阻礙。

針對以上問題，本文在對拉格朗日方程中約束反力與拉格朗日乘子關系的基礎上，指出乘子項是廣義位形空間中的廣義約束力，其實質是廣義約束力中各個約束所占的權重。利用拉格朗日增廣法計算機構的關節反力，詳細說明每個關節對應關節反力的計算方法和篩選步驟。為了證明計算方法的正確性，利用牛頓歐拉方程對所選模型關節反力再次求解，并應用ADAMS對同一模型進行動力學仿真，將所得的三種結果進行了對比。本文雖然以雙搖桿機構為例，所受約束為理想約束，但由于求解過程對約束方程與結構特性沒有特殊要求，保證了該方法對空間任意機構系統關節反力求解的適應性和準確性。

1 拉格朗日乘子的含義

第一類拉格朗日方程是應用數學分析中的乘子法建立的動力學方程。對于機構系統中任意構件其完整的表達式為[13]

(1)

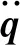
(2)

式中：F為廣義外力；Qc為約束反力。比較式(1)和式(2)明顯可得約束力與拉格朗日乘子之間的關系

(3)

2 關節反力計算與篩選

約束方程是在建立系統模型時，系統的狀態變量必須滿足一定條件所構成的方程。機械系統關節約束方程數等于該處關節反力個數且與該關節自由度數之和為3(平面)或為6(空間)[14]。設q為機構系統廣義坐標，C為機構約束方程，對C關于廣義坐標求一階和二階偏導可得機構的速度和加速度約束方程

(4)

(5)

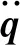
(6)

當約束方程中包含驅動約束方程時，雅克比矩陣為方陣，且通常為非奇異矩陣，即m=n，當約束方程中不包含驅動約束方程時，雅克比矩陣不為方陣，即m≠n。將式(6)與動力學方程式(1)聯立可得到系統完整的動力學模型

(7)

將剛體質量矩陣M、雅克比矩陣Cq、合外力矢量Qe以及Qd代入式(7)即可求得拉格朗日乘子λm×1，其標量形式可以寫為

λ=[λ1，λ2,...,λm]T

(8)

假設機構總運動副個數為A，構件數為b，第a個運動副自由度為Fa(a的取值規則與關節反力計算結果無關)，則機構總的約束方程個數m和機構廣義坐標個數n分別為

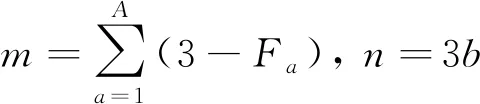
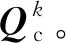
(9)

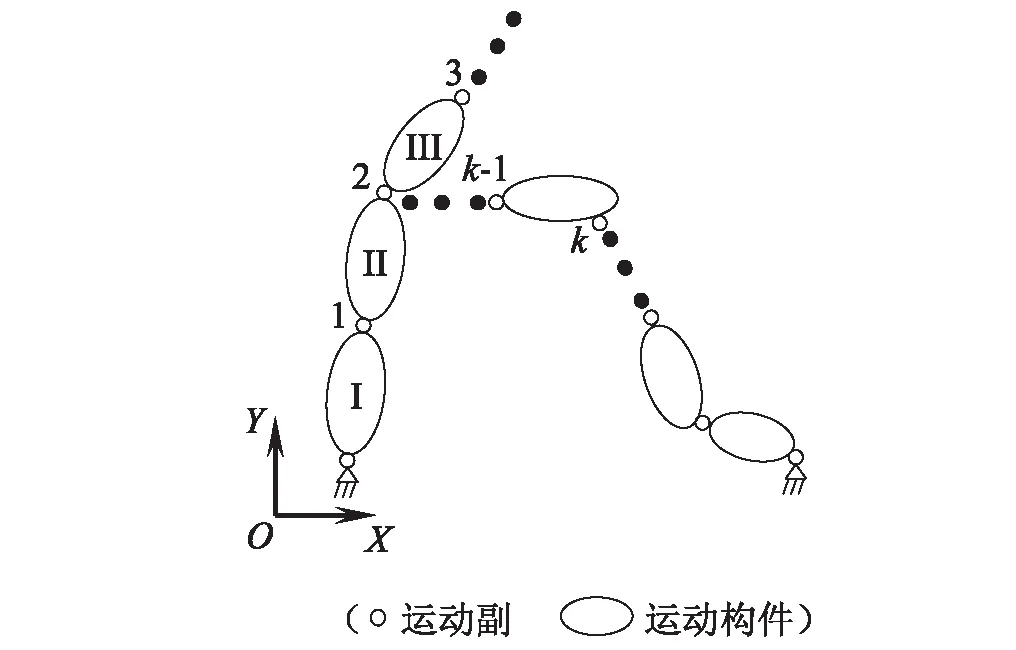
圖1 機構系統運動副Fig.1 Kinematic pairs in mechanism system

同樣，與該運動副相關的拉格朗日乘子(λ)k為機構系統乘子項λ中的第l+1行至第l+3-Fk行，即

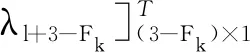
(10)

將式(9)轉置與式(10)代入式(3)得

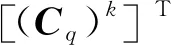
(11)

(12)

再次取所有廣義關節反力項N中與該運動副相關的關節反力，即N中的第l+1行至第l+3-Fk行

(13)

上述計算方法和篩選步驟的整個求解過程對系統的結構特性并無特殊要求，適用于空間機構系統，因此可以得出選用拉格朗日增廣法求解任意機構系統關節反力的一般步驟：

步驟1根據機構運動學已知條件求解約束方程C，并對約束方程關于廣義坐標求偏導得到雅克比矩陣Cq，提取雅克比矩陣Cq中與待求關節相關的分量并轉置；

步驟2同樣方法，提取拉格朗日乘子λ中與代求關節相關的拉格朗日乘子分量；

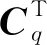
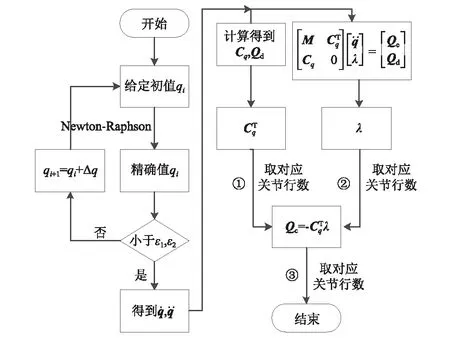
圖2 關節反力計算流程圖Fig.2 Calculated flow chart of reaction force

3 數值算例

以平面四桿機構OABC為例，簡圖如圖3所示。表1給出各均質桿件結構參數，轉動慣量相對質心。由于各桿長關系滿足l1+l4≤l2+l3，因此該機構為雙曲柄機構，即驅動桿和從動桿均可做整周回轉。桿l2為驅動桿，逆時針勻速轉動，轉速50π rad/s，計算時間t從0～0.4 s即一個周期內各構件的位置、速度和加速度。取桿件質心建立局部坐標系，系統坐標系O1XY，原點位于O，X軸與桿l1重合，方向指向C點。

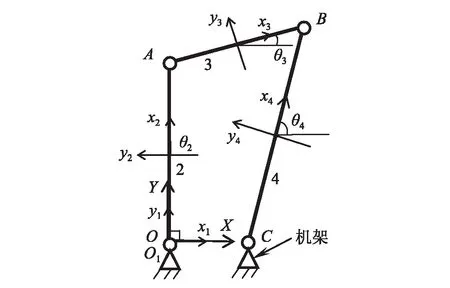
圖3 四桿機構簡圖Fig.3 Diagram of planar four-bar mechanism

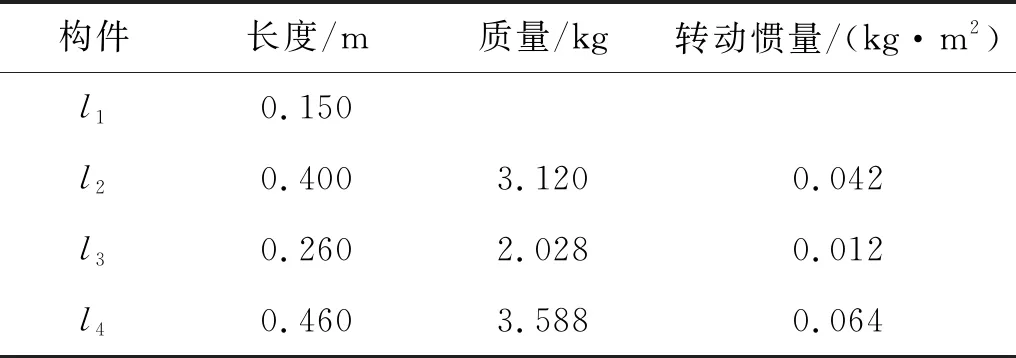
表1 四桿機構參數Tab.1 Parameters of four bar mechanism

為了證明上述拉格朗日增廣法求解各個關節對應關節反力選擇步驟和方法的正確性，利用牛頓歐拉方程對所選模型各關節反力重新計算。設桿件質量為m，選用質心坐標為廣義坐標q=(Rx,Ry,θ)，根據桿件受到與其相鄰構件i和j的力和力矩平衡條件，可列出如下矢量表達式

(14)

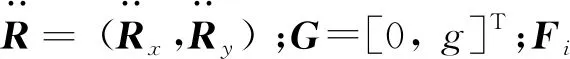
同樣選用四桿機構OABC為對象，利用ADAMS軟件建立三維仿真模型如圖4所示。并進行動力學仿真分析，求解各個關節接觸反力。

ADAMS簡化模型在時間t從0～0.4 s即一個周期內進行仿真，得到各個關節的關節反力及x向和y向的分力，將結果與前兩節的數值結果進行對比如圖5～圖8所示。

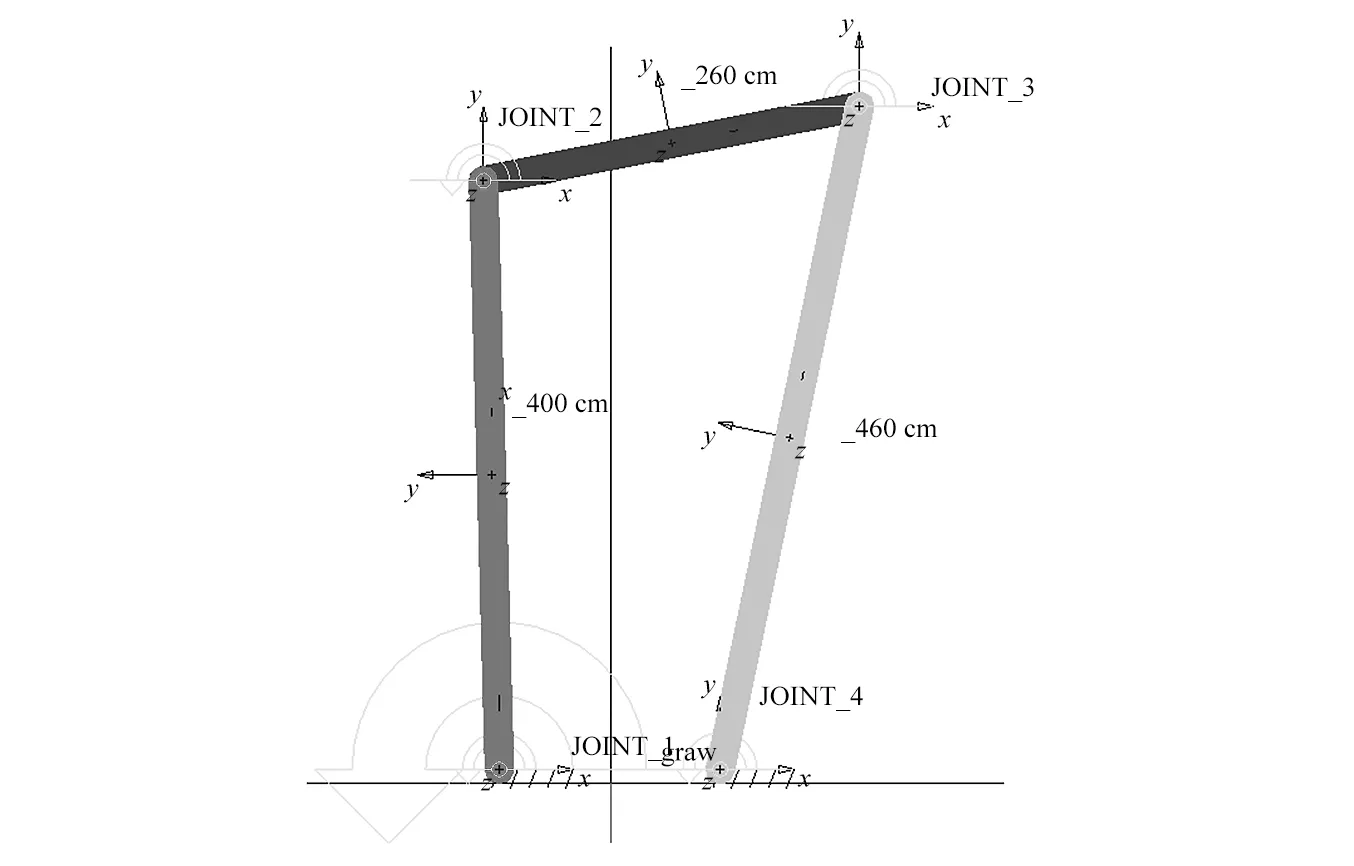
圖4 ADAMS仿真模型Fig.4 ADAMS simulation model

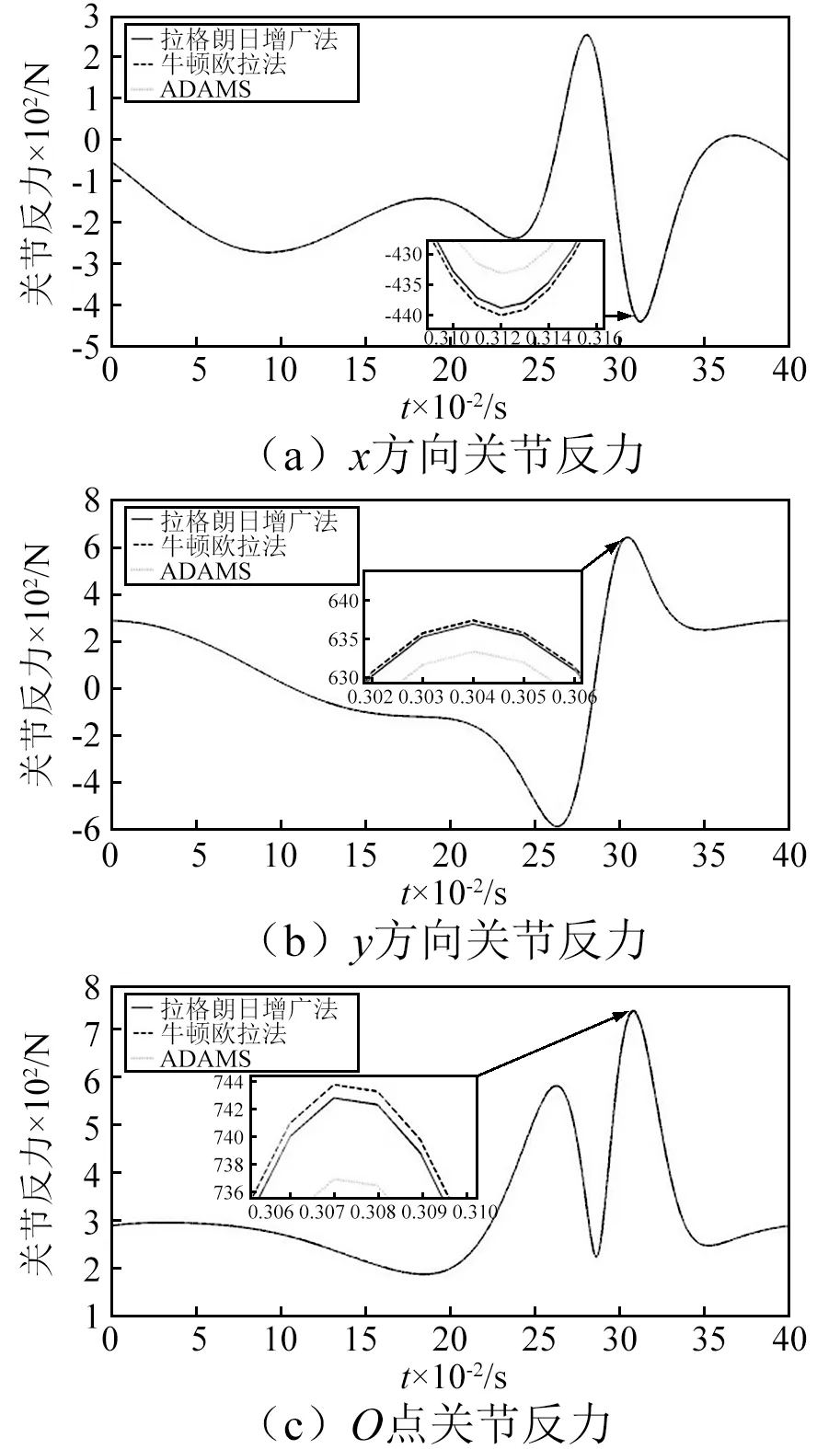
圖5 O關節反力及分量Fig.5 Reaction force and components at point O

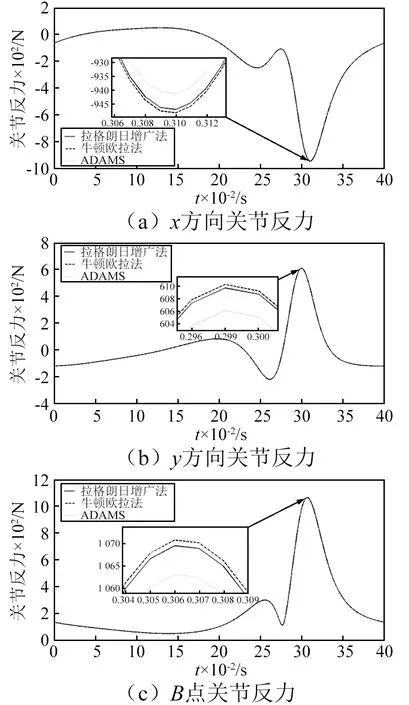
圖7 B點關節反力與分量Fig.7 Reaction force and components at point B

分析圖5～圖8中數值計算與ADAMS仿真結果曲線可得以下結論：

(1)拉格朗日增廣法對所選雙搖桿機構各關節處關節反力計算結果與其他兩種方法計算結果相比略有誤差，但不影響本次對關節反力計算方法與篩選步驟的討論。

(2)拉格朗日增廣法計算關節反力產生誤差的原因主要是由于初始坐標位置精度不同、給定計算結果誤差等級不夠以及動力學方程組求解過程中出現的約束違約等原因造成。

(3)三種計算方法所得各關節處關節反力變化曲線基本重合，符合四桿機構實際的運動規律和動力學特性，可以證明文中拉格朗日增廣法求解關節反力計算方法和篩選步驟的正確性。

4 結 論

(1)針對長期以來對拉格朗日乘子法中涉及拉格朗日乘子是否為系統真正關節反力的問題，明確了拉格朗日乘子中的乘子項是廣義位形空間中的廣義約束力而非真正的關節約束反力。

(2)利用拉格朗日增廣法計算機構的關節反力，詳細說明每個關節對應關節反力的計算步驟和方法，并以雙搖桿機構為例對一個周期內的所有關節的關節反力進行數值求解。

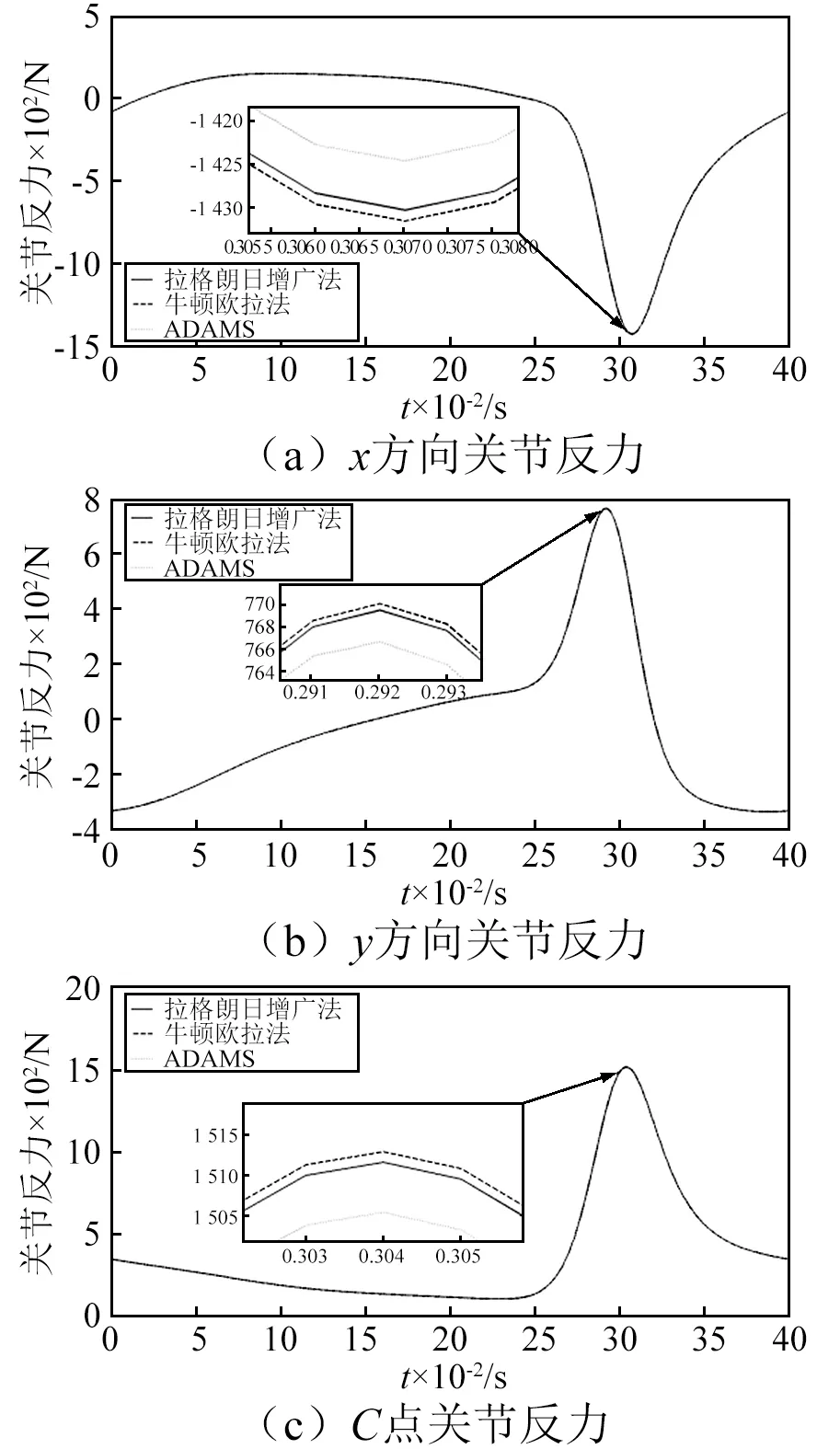
圖8 C點關節反力及分量Fig.8 Raction force and components at point C

(3)為了驗證計算方法和選擇步驟的正確性，利用牛頓歐拉方程與ADAMS軟件對同一模型進行動力學數值仿真，通過使用不同方法求得的各關節反力相同，且誤差在允許范圍之內。

(4)關節反力計算方法與篩選步驟雖然以雙搖桿機構運動一周各個關節所受關節反力的計算與篩選為例，但通過第二部分論述，該方法可使用于空間任意機構系統的關節反力計算。