紅外瓦斯傳感器檢測中噪聲點研究*
程文娟,黃星星,湯世祥,童 兵,周淼淼
(合肥工業大學 計算機與信息學院,安徽 合肥230009)
0 引 言
常用煤礦瓦斯檢測儀按其工作方式可分為催化型、熱傳導式、氣敏半導體型和紅外型等[1]。但是催化型存在零點漂移和靈敏度衰減的問題[2]、熱傳導式易受到水蒸汽等其他氣體的影響、氣敏半導體型的測量范圍窄而且精確度低。因為紅外型瓦斯檢測儀具有測量范圍廣、響應速度快、壽命長、不易中毒等優點已被廣泛應用于煤礦環境中易燃易爆氣體濃度的檢測[3]。但由于紅外瓦斯傳感器檢測儀易受煤礦環境中的溫度、濕度、壓力等復雜的物理環境因素影響,使檢測瓦斯濃度值不準確,一般有硬件和軟件兩種方法來解決這一問題。但由于通過硬件改進的方法價格昂貴,一般傾向于采用軟件方法。近些年有很多文獻撰寫了關于采取軟件的方法設計紅外瓦斯傳感器,如參考文獻[4~6]等,其中較為經典的軟件方法是參考文獻[4]所述選用防脈沖平均濾波算法,該算法的基本思想是去掉n個采集數據集中最大值和最小值,然后計算剩下所有樣本的平均值。此方法比較簡單且易行,但存在著如果采集數據量n 值偏大時靈敏度會降低的缺點。參考文獻[5]用線性最小二乘法分別計算出采集數據集中的最大和最小的理想值,將最大和最小理想值的差值帶入相應公式計算出瓦斯濃度值。這樣不僅保證數據的連續性,而且具有較高檢測響應時間,但該方法工作效率低。參考文獻[6]基于RBF 神經網絡對采集數據處理,這種方法能夠消除環境中溫度和濕度因素對瓦斯濃度檢測的影響,但沒有考慮其他物理環境和硬件本身因素對瓦斯濃度測量值的影響。
本文將與基準數據偏差較大的點定義為噪聲點。首先,利用分化距離與K-means 算法結合方法找出采集數據中可能的噪聲點;其次,根據孤立度系數判斷真正的噪聲點;再次,對噪聲點做直接丟棄處理,這樣做可以提高軟件工作效率;最后,對處理之后的剩余采集數據集計算平均值即為測量的瓦斯濃度值,實驗結果表明:該方法測試出的瓦斯濃度的誤差小于1%,精度高。
1 相關理論
1.1 朗伯—比爾定理
紅外型瓦斯傳感器是基于分子振動和轉動吸收譜與發光光譜的一致性原理而制成的[7]。當紅外光透過待測氣體時,紅外光的強度會變弱,氣體對紅外光的吸收遵循朗伯—比爾(Lambert-Beer)定律

式中 I 為透射光強度;I0為入射光強度;K 為吸收截面系數;L 為紅外光透過氣體層的厚度;C 為待測氣體的濃度。根據入射光和透射光的強度便可計算出氣體的濃度C。
1.2 分化距離
分化距離是指計算任意兩數據點的實際距離D(i,j)和任意兩點距離中最大距離dmax,選取分化度φ(0 <φ <1),對所有的D(i,j)做分化處理,便得到分化距離d(i,j)[8],其關系式為

式中 d(i,j)為分化距離;φ 為分化度;D(i,j)為兩點間實際距離。任意兩點距離D(i,j)與距離集中最大距離dmax的比值Θ(i,j)為

式中 D(i,j)為兩點間實際距離;dmax為距離集中的最大距離。如果Θ(i,j)<φ,則D(i,j)<d(i,j);否則D(i,j)≥d(i,j),分化距離的思想是使原本能靠近的兩個數據更緊密,原本距離較遠的兩個數據變得更遠。
1.3 K-means 算法模型分析
K-means 算法是關于數據集相似度的聚類算法,是一種非監督學習方法[9]。在中小規模的樣本數據的聚類采用此方法有很好的效果。
根據參考文獻[10]中所述K-means 算法主要思想,首先,需要隨機選取初始聚類的K 個中心點;其次,計算所有剩余的數據集到中心點的歐氏距離,將距某一中心點最近的數據點歸并到該聚類;最后,用均值法調整聚類的中心點計算收斂函數,不斷重復上述步驟,直至收斂函數的值最小為止。
對于一系列時間間隔相同的數據點,可將K-means 算法的思想簡化為如下步驟:
1)在數據集D 中隨機的選擇K 個點β1,β2,β3,…,βk作為聚類簇C1,C2,C3,…,CK的聚類中心點;
2)計算不在聚類簇的數據集中的點di各個簇類中心點的歐氏距離,并將距di最近的點分配到Cj類

3)對于簇Cj,重新計算簇Cj的質心βj;
4)計算收斂函數,并判斷收斂函數的值是不是最小,其中收斂函數如式(5)所示

2 采集數據處理與模型建立
實驗設計紅外瓦斯傳感器選用單光路雙波長的設計方案,紅外瓦斯傳感器系統示意圖如圖1 所示。
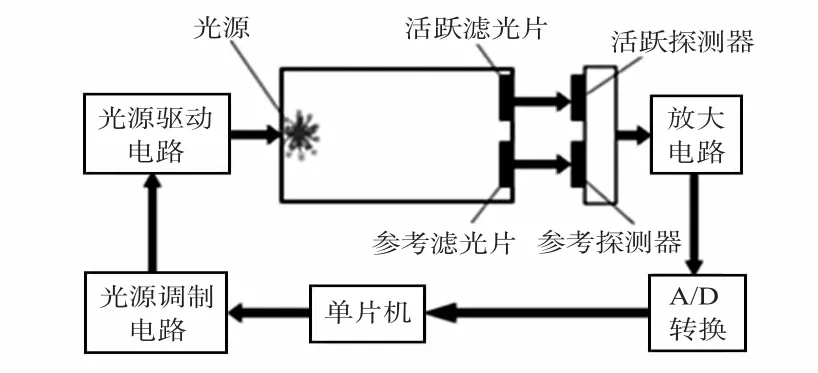
圖1 紅外瓦斯傳感器系統示意圖Fig 1 Diagram of infrared gas sensor system
紅外瓦斯傳感器系統中光源為IRL715;探測器為PYS3228,該探測器含兩個獨立的濾光片和探測器。其中,單片機不僅控制光源調制電路和光源驅動電路,而且可以顯示檢測的瓦斯濃度值。
用實驗設計的系統采集120 個數據作為采集數據集D={x1,x2,…,xi…,x120},將此120 個數據分為3 組,每組40 個數據點,首先,計算相鄰兩個數據xi,xi+1絕對值ai,絕對值的集合為A={a1,a2…,ai,…,a39},如果相鄰數據差的絕對值較小,則這兩個數據點很可能是在同一聚類簇中;其次,對集合A 中的數據點做分化距離處理后得到的集合S={s1,s2,…,sx,…,s39};最后,用K-means 算法對集合S進行聚類,可得到不同的聚類簇中心值和各個聚類簇中的數據點,選擇聚類中心點值最大的簇作為虛擬噪聲點的集V={d1,d2,…,dm}。
根據虛擬噪聲集合V 中數據點查找在集合D 中對應的數據值,求出這些數據點的前后相鄰數據點的孤立系數,并分別將某一數據點與其前后相鄰的數據點計算的孤立系數的值分別叫前孤立系數和后孤立系數。孤立系數的表達式為

式中 xi與xi+1為相鄰的兩數據點,f 為采樣頻率。將θ 與給定的閾值ε 比較,如果θ≥ε,則孤立度高;否則,孤立度低。
如果一個數據點的前孤立系數和后孤立系數均大于閾值ε,則此數據點為噪聲點,如果一個數據點與其前相鄰的孤立系數高與其后相鄰的孤立系數低,或者相反,如圖2 所示,可將其視為轉折點。
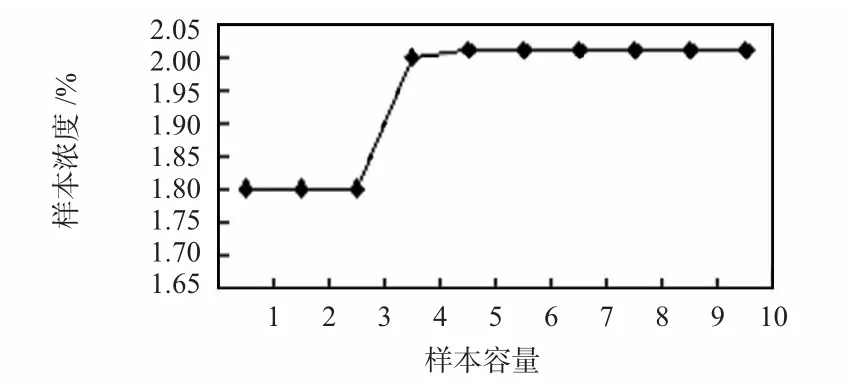
圖2 轉折點示意圖Fig 2 Diagram of turning point
根據以上設想,將某一數據點的前、后孤立系數與給定的閾值比較,即可判斷此數據點是不是噪聲點。可用如表1所示的噪聲點判定表判斷。

表1 噪聲點判斷表Tab 1 Noise point determination
如果判定xi是噪聲點,可以直接將其丟棄,假設噪聲點有m 個,分別為{x1,x2,…,xm},丟棄噪聲點之后的有用數據為{x1,x2,…,x40-m},選用式(7)均值法計算濃度值

通過上述對數據集處理過程的描述,得到樣本處理點的流程圖如圖3 所示。
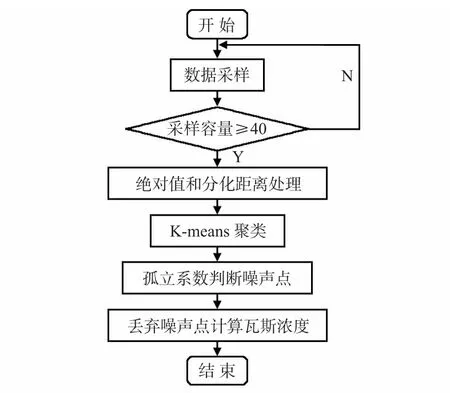
圖3 樣本處理流程圖Fig 3 Flow chart of sample processing
3 實驗結果與分析
本文中K-means 算法中K=4,f=0.5 Hz,根據經驗可知孤立系數閾值為ε=arctan 0.03,分化度為φ=0.01。
本文選取濃度為2%的標準瓦斯濃度分別選用基于分化距離與K-means 算法結合的方法處理采樣值與不做任何處理采樣數據集可得到如圖4 所示的實驗結果對比圖。由圖4 可以看出:基于分化距離與K-means 結合的方法處理數據集之后的數據集中的噪聲點明顯比不做任何處理的采集數據集中的噪聲點的數目減少,所以,此方法檢測的瓦斯濃度值的準確度高。
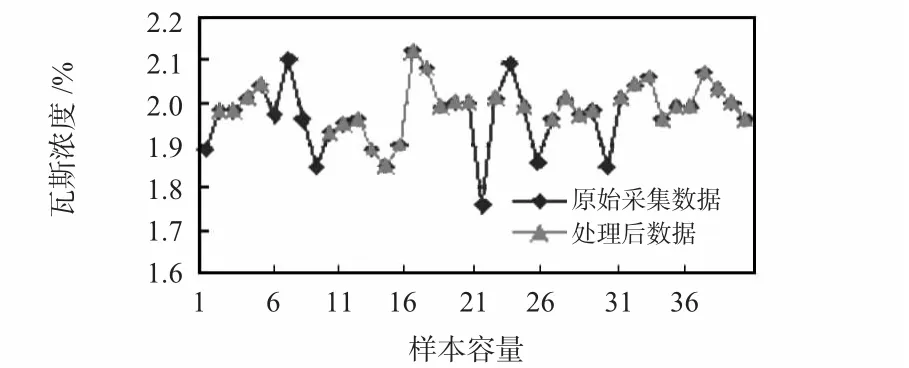
圖4 實驗結果對比圖Fig 4 Comparison of experimental results
本文對標準瓦斯濃度的選取值小于5%,經過采用基于分化距離與K-means 算法結合方法,通過聚類和判斷噪聲點等過程的處理,可得實驗結果對比分析表如表2。

表2 實驗結果對比分析表Tab 2 Comparison and analysis of experimental results
從表2 可以看出:基于分化距離與K-means 算法結合方法檢測瓦斯濃度小于1%,而且具有較高的精確度。
4 結束語
本文提出了一種基于分化距離與K-means 算法結合的方法,對采集一段時間采集數據集處理,再根據前后孤立系數判斷噪聲點,計算濃度值。經過實驗證明了此方法的有效性,由實驗結果可看出:此方法檢測的瓦斯濃度值小于1%,測量精確度高,適用于礦井的復雜環境。除此之外,本方法還可應用于其他氣體測試。
[1] 張 雷,尹王保.基于紅外光譜吸收原理的紅外瓦斯傳感器實驗[J].煤炭學報,2006,31(4):480-483.
[2] 于 震,張正勇.熱催化瓦斯傳感器的特性及其補償方法[J].傳感器與微系統,2010,29(1):42-44.
[3] 葉瑋琳,鄭傳濤.中紅外甲烷檢測儀穩定性實驗及溫度補償研究[J].光學學報,2014,34(3):273-277.
[4] 呂光潔.光譜吸收式煤礦瓦斯紅外檢測技術的應用研究[D].西安:西安科技大學,2009.
[5] 趙 聰.基于非色散紅外光譜吸收原理的瓦斯濃度檢測儀設計[J].計算機測量與控制,2009,17(6):1229-1231.
[6] 張 麗,王汝琳.基于神經網絡的礦用紅外瓦斯傳感器檢測模型的研究[J].工礦自動化,2009(8):18-21.
[7] 羅達峰,楊建華.基于紅外吸收光譜的瓦斯氣體濃度檢測技術[J].光譜學與光譜析,2011,31(2):384-386.
[8] 劉 歡,吳介軍.基于分化距離的離群點檢測算法[J].計算機應用研究,2010,27(9):3316-3318.
[9] Han Jiawei,Kamber Micheling,Pei Jian,et al.數據挖掘概念與技術[M].范 明,孟小峰,譯.北京:機械工業出版社,2012.
[10]周愛武,于亞飛.K-means 聚類算法的研究[J].計算機技術與發展,2011(2):62-65.

