ACO-BP 神經網絡在電梯交通流預測中的應用*

萬健如，賈祖新，智 淵

(1.天津大學 電氣與自動化工程學院，天津300072;2.重慶能源職業學院 電梯學院，重慶402260)

0 引 言

隨著高層智能建筑的興起，電梯配置和群控調度對于樓宇內垂直交通效率的影響越來越大［1］。合理有效的電梯交通流預測是電梯配置和群控調度的基礎，可為其提供必需的交通數據信息［2］，使系統可依據獲得的不同時段的客流強度，識別上下高峰、隨機層間等不同交通模式，并以此實現最佳配置和最優調度。

電梯交通流預測研究自20 世紀80 年代以來，出現了時間序列模型、指數平滑模型、神經網絡法、非參數回歸、支持向量機等方法［3～5］。其中，基于BP 神經網絡的電梯交通流預測模型發展迅速，但傳統的BP 算法具有對初值敏感、訓練時間長、易陷入局部極小值、預測精度低等缺點，這雖可通過附加動量法、自適應學習率、牛頓法等進行改進，但均存在局部極小問題和場合局限，不能滿足現代建筑智能化的要求。本文提出利用蟻群優化(ACO)的BP(ACO-BP)神經網絡進行全局優化，利用天津某大廈實際交通流數據對模型進行仿真驗證，結果表明了本文提出ACO-BP 神經網絡應用于電梯交通流預測系統的有效性。

1 交通流預測模型

1.1 電梯交通流分析

電梯交通流是由乘客數、乘客出現的頻率以及乘客在樓層的分布情況所描述的狀態量［4］，其特性與建筑大樓類型息息相關。本文以5 min 作為時間間隔，通過統計進出某辦公大樓的總乘客數，得到交通流時間序列{x(ti)，i=1，2，3，…，n;ti=i×td;td=5 min;}。交通流時間序列具有非線性、隨機性和高度的復雜性，甚至表現出混沌特性，很難用一個確定完整的函數表達式來描述，而神經網絡可在不建立精確數學模型的情況下逼近任意非線性映射，非常適合電梯交通流預測系統的建模。

1.2 神經網絡預測模型

1.2.1 網絡結構

理論上已經證明:在合適的結構和權閾值的情況下，包含一個S 型隱含層和一個線性輸出層的3 層BP 網絡可以逼近任意有理函數［6］。因而，本文采用具有單隱含層的BP神經網絡，隱含層和輸出層分別采用對數S 型和線性激活函數，其拓撲結構如圖1 所示。

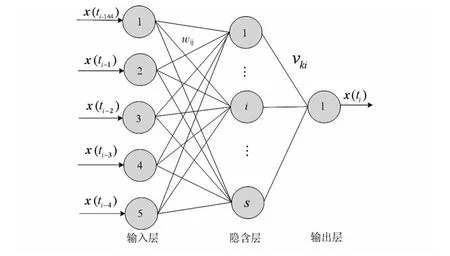
圖1 BP 網絡結構圖Fig 1 Architecture of BP neural network

輸入矢量和輸出矢量分別為

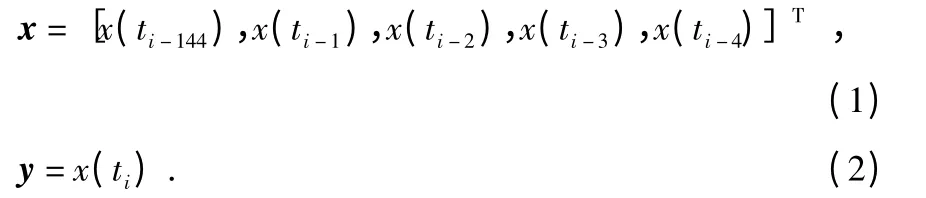
隱含層節點數是影響神經網絡性能的關鍵，太少不足以提取出樣本的內在規律，太多又會造成過度擬合。目前，關于隱含層節點數的確定在理論上還不成熟，本文根據Kolmogorov 定理［7］來確定基本節點數，并在此基礎上增加節點數進行試湊，以得到最佳隱含層節點數。

1.2.2 BP 算法

本文采用批訓練方式調整權值，定義誤差函數為

采用梯度下降法進行推導，對輸出層而言，第i 個輸入到第k 個輸出的權值和閾值變化量分別為

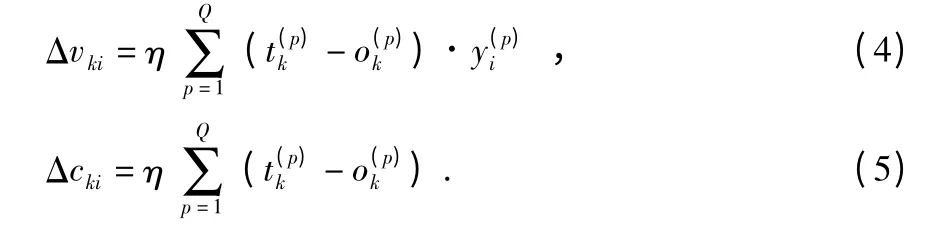
同理，隱含層第j 個輸入到第i 個輸出的權值和閾值變化量分別為

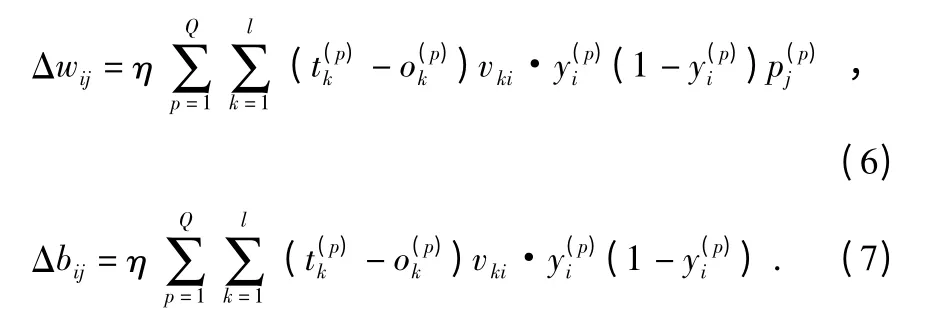
1.2.3 BP 算法改進

針對BP 算法的缺點，目前已有附加動量法、自適應學習率等一些比較成熟的改進方法［8］。以附加動量法為例，改進后的網絡權值調整公式為

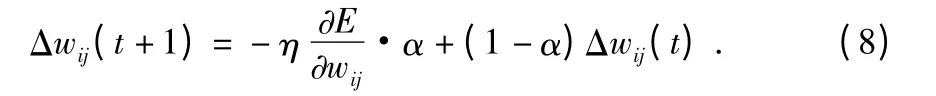
其中，α(0 ＜α ＜1)是動量因子。

附加動量法積累了前一次權值調整的經驗，雖可使網絡滑過某些局部極小值，但在某些場合下仍會使網絡出現振蕩且沒有足夠能量跳出低“谷”。

2 ACO-BP 神經網絡

ACO 算法具有良好的分布式計算和全局尋優能力，并且易于與其他方法融合［9］。而對于經典ACO 算法過度搜索與抉擇困惑的問題，本文利用精英螞蟻和優化排序策略進行改進。

2.1 ACO-BP 神經網絡的策略

ACO 算法優化神經網絡主要通過改進樣本學習訓練過程實現，具體實現過程如下:

1)確定參數個數n，包括網絡中所有的權閾值。每個參數pi(i=1，2，…，n)對應一個有N 個元素的集合Ipi，這些元素為pi的可能取值。候選值個數N 并非越大越好，過多的候選值對于規避局部極小值的作用不大，反而會增加蟻群工作量，并且使神經網絡修正能力的發揮受限。

2)設置螞蟻數m，啟動所有螞蟻，每只螞蟻隨機選擇Ipi中的一個候選值，然后螞蟻按概率選擇下一個集合的某個元素，直至每只螞蟻均在n 個集合中各選擇了一個候選值。對于螞蟻k(k=1，2，…，m)，其選擇Ipi中第j 個元素的概率為

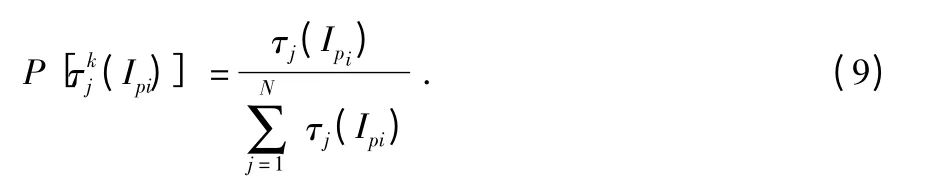
其中，τj(Ipi)為集合Ipi中第j 個元素的信息素的值。為避免搜索陷入螞蟻最初產生的幾條路徑中，信息素的初始值不應太小。

3)經過上述步驟之后，m 只螞蟻構建出m 組權閾值組合，分別計算每個組合所對應的網絡輸出和誤差，并按照誤差從小到大排序，記錄本次循環最優解。當m 只螞蟻全部周游完成一次循環之后，根據下式更新信息素

其中，ρ∈(0，1)是ACO 算法中表征信息素留存能力的重要參數。ρ 太小會使收斂太快，解的質量不好;ρ 太大會增大搜索范圍，收斂太慢。考慮極限情況，令ρ=1，即不使用信息素蒸發機制，信息素就會無限積累，算法是不會收斂的。

式(10)混合了精英和優化排序策略。在優化排序策略下，輸出誤差最小的前δ 只螞蟻多釋放出的信息素的總增量為

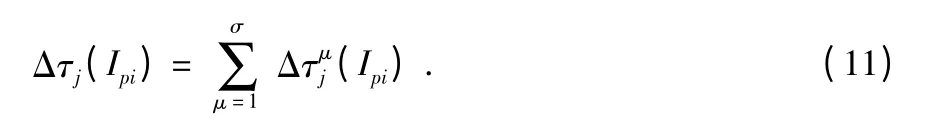
其中，μ 為螞蟻排序號。當第μ 只螞蟻選擇了第j 個元素，其信息素的增加)為

否則為0。其中，Q 為信息素固定值;eμ為第μ 只螞蟻對應的神經網絡輸出誤差。

否則，為0。其中，e*為精英螞蟻至此找到的最優解對應的輸出誤差。

4)重復步驟(2)，(3)，直到輸出誤差滿足ACO 算法要求或者循環次數達到上限。

5)將蟻群最終搜索到的權閾值組合作為神經網絡的初始值，利用BP 算法訓練網絡，進一步修正權閾值，直到滿足要求。

2.2 程序流程圖

基于以上ACO—BP 神經網絡的過程，得出如圖2 所示的優化算法的整體流程圖。

3 應用實例

利用天津某辦公大樓的實際交通流數據進行分析，統計該辦公大廈周一～周五共5 個工作日內每天7:00～19:00 每5 min 內進出大樓的總乘客數，共得到720 個數據。

由于隱含層的S 型函數對零點附近的輸入信號放大程度較好，而當凈輸入較大時，神經元的輸出將趨于飽和，放大效果不是很明顯。因而需要將這720 個數據統一歸一化到區間［0，1］中，即得到樣本數據。

3.1 各層節點數的確定

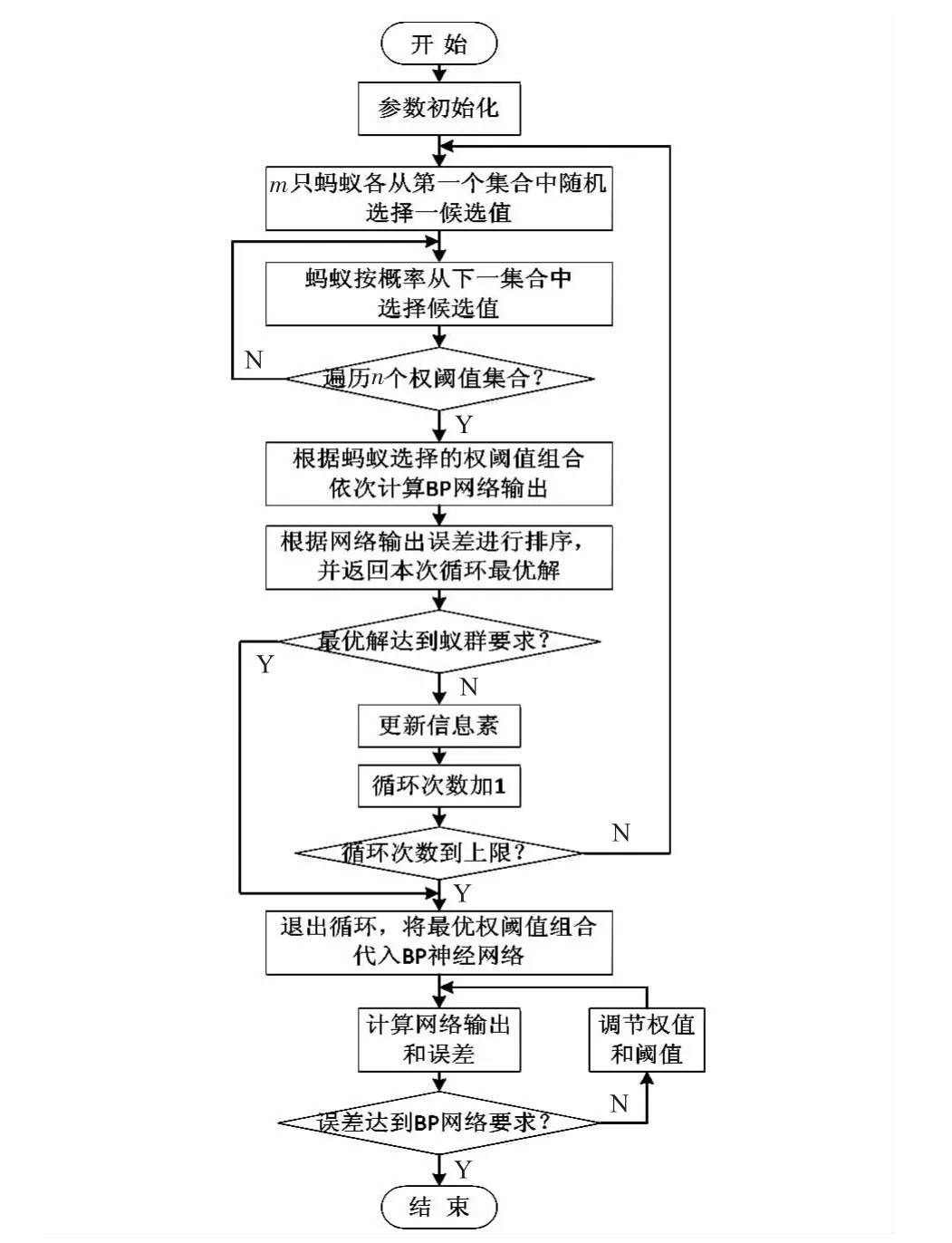
圖2 ACO—BP 網絡算法流程圖Fig 2 Flow chart of ACO—BP neural network algorithm

對于電梯交通流而言，t 時刻的交通流與當天前2 個時刻以及前天同一時刻的交通流相關性最大。為了更好地反映交通流的變化以及數據間的內在聯系，如圖1 所示，本文利用當天前4 個時刻和前天同一時刻的交通流來預測當天某一時刻的交通流，即輸入節點數為5，輸出節點數為1，由此，確定基本隱含層節點數應為11，然后，在此基礎上加上一些余量進行試湊。

表1 給出了當誤差目標為0.01，采用BP 算法訓練時，具有不同隱含層節點數的網絡所需的訓練時間與循環次數，可知隱含層節點數取13，15 為最佳，本文取13。

表1 網絡訓練結果Tab 1 Network training results

3.2 仿真分析

確定網絡權閾值參數個數為92，將區間［－5，5］等分為100 份，利用Matlab 中rands()函數在每個小區間中隨機產生一個數作為候選值，最終每個參數對應一個有100 個候選值的集合;經過反復的匹配與調整，最終選定100 只螞蟻，信息素留存系數ρ 取0.8，信息素初始值取8 000，σ 取20，Q 取1。

取前4 天的數據作為訓練樣本，第五天的數據作為測試樣本，由此可得到572 組訓練樣本和144 組測試樣本，編制m 文件分別對基于BP 與ACO—BP 神經網絡的電梯交通流預測模型進行仿真分析，并對傳統的BP 算法利用附加動量法進行改進。設置最大迭代次數為40 000，均方差目標為0.002，為了弱化隨機性的影響，分別運行3 次，對比最終的訓練誤差，結果如圖3 所示。

圖3 三次運行結果對比Fig 3 Comparison of three running results

由圖3 可知，3 次運行中，傳統的BP 神經網絡即使經過附加動量法改進之后仍然全部陷入了0.003 93 這個極小值點;而ACO—BP 神經網絡3 次全部達到訓練誤差要求0.002。

取其中一次的運行結果進行對比分析，具體結果如表2所示;圖4 ～圖7 所示分別為傳統BP 和ACO-BP 神經網絡的訓練誤差性能曲線和模型預測擬合曲線。

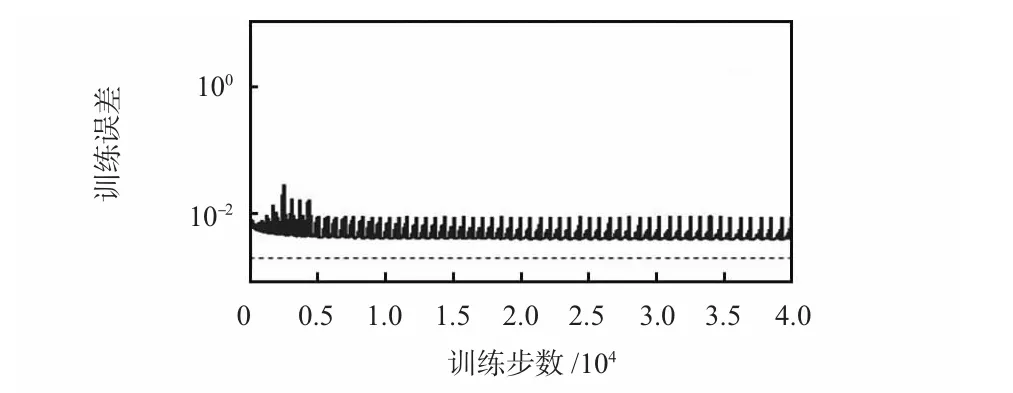
圖4 傳統BP 神經網絡的訓練誤差性能曲線Fig 4 Training error performance curve of BP neural network

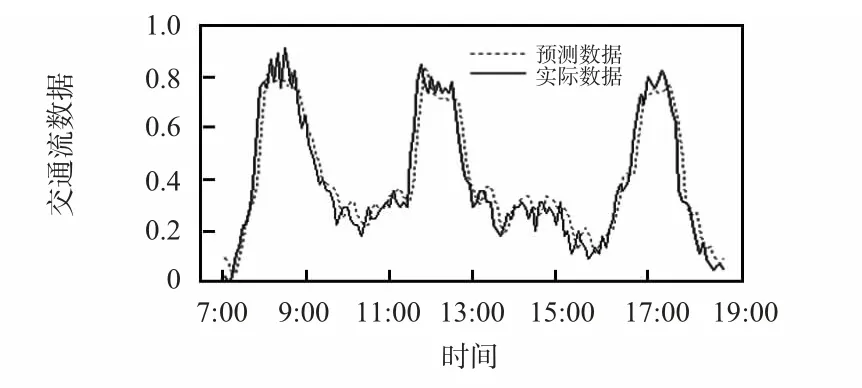
圖5 傳統BP 神經網絡模型的預測和擬合曲線Fig 5 Forecasting and fitting curve of traditional BP neural network model

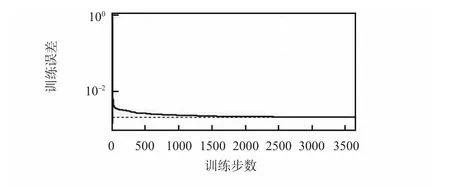
圖6 ACO—BP 神經網絡的訓練誤差性能曲線Fig 6 Training error performance curve of ACO—BP neural network

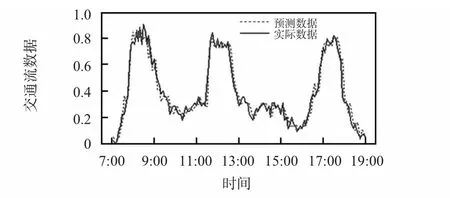
圖7 ACO—BP 神經網絡模型的預測和擬合曲線圖Fig 7 Forecasting and fitting curve of ACO—BP neural network model

圖4 所示訓練過程耗時447 s，在開始的5 000 步，網絡在跳過某些局部極小值之后，誤差由初始值1.18 降到0.004左右，之后網絡便陷入了一個長達3 0000 多步的振蕩過程，并且最終誤差只達到0.003 93，此時網絡完全陷入這個局部極小值。對比圖6，整個訓練過程耗時88 s，初始誤差僅為0.276，只用3 638 步就達到誤差目標0.002，并且整個訓練過程很平滑，未受到局部極小值的影響。

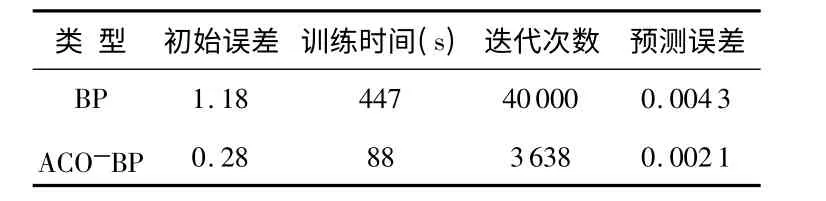
表2 ACO—BP 與BP 神經網絡預測結果對比Tab 2 Prediction results comparison of ACO—BP and BP neural network

對比圖5 和圖7 可知，二者均可以較好地預測交通流的變化趨勢，對于客流高峰時段的預測也都在合理范圍內。但二者的預測精度是有差別的，圖5、圖7 的預測誤差分別為0.004 3和0.002 1，而且圖7 的預測曲線能很好地反映交通流短時間內很小的變化。

綜上所述，ACO—BP 神經網絡不但克服了傳統BP 神經網絡的局部極小值問題，而且在訓練時間和預測精度上也有優勢。

4 結束語

本文在建立的基于BP 神經網絡交通流預測模型的基礎上，針對BP 算法的缺點，提出ACO—BP 算法，該方法兼具ACO 算法全局尋優和BP 網絡廣泛映射等優點;采集天津某辦公大廈的實際交通流數據對建立的ACO—BP 神經網絡交通流預測模型進行仿真，結果表明:ACO—BP 神經網絡訓練時間短、預測精度高，這可為電梯配置與群控提供更為準確的交通流信息。

［1］ 萬健如，張彥朝，楊岳楓.電梯選型配置與優化設計研究［J］.中國電梯，2009，20(21):21－26.

［2］ Ding Bao，Zhang Yongming，Peng Xiyuan，et al.A hybrid approach for the analysis and prediction of elevator passenger flow in an office building［J］.Automation in Construction，2013，35:69－78.

［3］ 唐海燕，于德亮，丁 寶，等.基于SVR 的電梯交通流時間序列預測［J］.控制工程，2011，18(5):723－726，792.

［4］ 黃 敏，崔寶同，顧樹生.基于小波神經網絡的電梯交通流預測［J］.控制與決策，2006，21(5):589－592.

［5］ 張曉利，陸化普.非參數回歸方法在短時交通流預測中的應用［J］.清華大學學報:自然科學版，2009，49(9):39－43.

［6］ 王旭東，劉金鳳，張 雷.蟻群神經網絡算法在電動車用直流電機起動過程中的應用［J］.中國電機工程學報，2010，30(24):95－100.

［7］ 徐華中，吳 蘇，劉 念.基于多傳感器數據融合技術的短時交通流檢測［J］.傳感器與微系統，2009，28(2):104－106，109.

［8］ 田秀梅.BP 算法的改進及仿真研究［J］.電子技術，2011，38(3):60，64－65.

［9］ Mavrovouniotis Michalis，Yang Shengxiang.Evolving neural networks using ant colony optimization with pheromone trail limits［C］∥Proceedings of the 13th UK Workshop on Computational Intelligence，Piscataway:IEEE，2013:16－23.