GPS控制網坐標轉換模型的研究
金儉儉,董彥鋒,王 茹,徐錄鑄,王維宇
(東南大學交通學院,江蘇 南京211189)
一、引 言
近些年來,GPS定位技術已廣泛用于控制測量等領域。GPS定位的成果屬于WGS-84大地坐標系,但我國目前應用的地形圖卻屬于1954北京坐標系或者1980國家坐標系,而不同的坐標系之間存在著平移和旋轉關系,因此應用GPS定位成果需要進行坐標轉換。我國的平面和高程兩個控制系統分別屬于不同的系統基準和坐標框架,故隨著控制測量區域面積的不同,3個坐標的變化規律呈現出復雜性,如較小區域的控制測量,為了減少長度變形,一般采用無須投影計算的平面直角坐標系統等,而在空間坐標轉換問題上需要考慮這些因素。
空間坐標轉換模型主要有布爾薩(Bursa)模型、莫洛金斯基(Molodensky)模型、范士模型和武測模型等。上述模型都包括3個平移參數,3個旋轉參數和1個尺度參數,因而稱為七參數轉換模型,本文就布爾薩模型在一定區域GPS控制測量中坐標向高斯直角坐標系的轉換進行探討,并在相同原理基礎上將其演變成九參數模型,以解決單一尺度不足問題。
二、坐標系相互轉換
1.空間直角坐標系統
如圖1所示,兩個空間直角坐標系之間存在3個平移量,對應的坐標軸之間存在3個微小的旋轉角,及兩坐標系之間的尺度比。
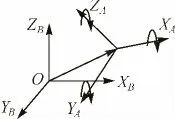
圖1 空間直角坐標系
2.布爾薩七參數轉換模型
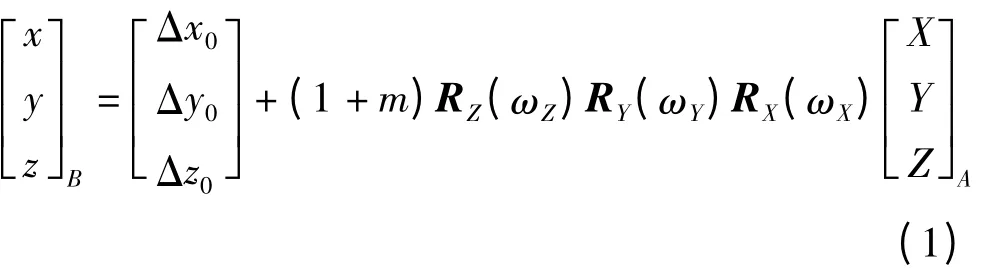
式中,B為1980西安坐標系坐標,A為WGS-84坐標系坐標。
其中3個旋轉參數為
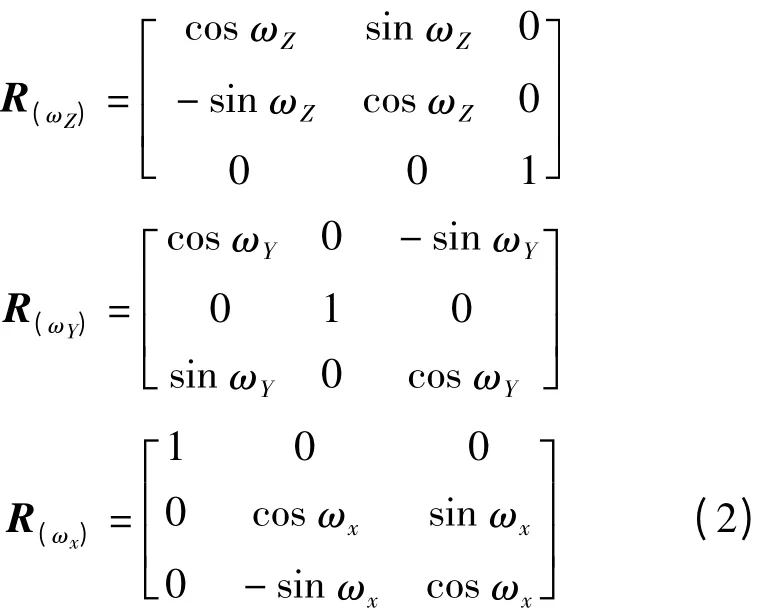
在小區域GPS控制測量中,考慮到旋轉角都是微小量,對同一點,有式(3)
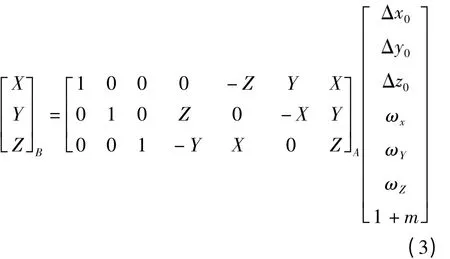
對式(3)進行整理變換,可得式(4)
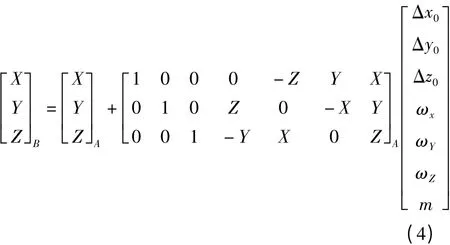
3.間接平差模型
依據式(4),若求七參數,只要有足夠多的重復點觀測,就可依據平差理論建立模型。這里按照間接平差模型V=Bδ^X-L建立相關的坐標轉換模型,在最小二乘原則下求解七參數。

式中,B矩陣中相關的坐標系數是WGS-84坐標系測得的數據坐標。
4.平差計算及精度評定
由于七參數轉換模型中有7個未知數,依據平差原理,需要至少進行坐標聯測3個點,每個點分別有x、y、z坐標數據。
設在一控制測量區域已經存在3個坐標點,其1980西安坐標系的坐標已知,然后利用GPS接收機聯測這3個點的坐標,得到WGS-84坐標系的坐標,分別為:( x1,y1,z1),( x2,y2,z2),( x3,y3,z3),將其代入,可得B矩陣。這里3個點坐標測量的精度相同,可設其權陣為單位陣。依據最小二乘法原理VTPV=min可得
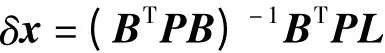
由此可以計算出七參數轉換模型中的7個參數,代入式(6)可以得到任意一點1980坐標系中的坐標。
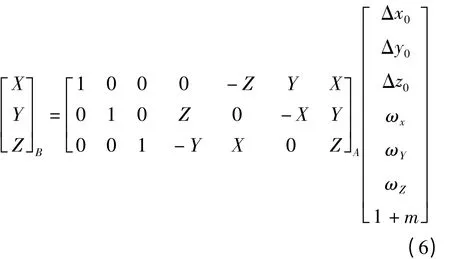
由此,兩個坐標系之間坐標轉換的模型就建立了。求出轉換參數后,依據轉換模型可求出公共點在新坐標系下的坐標,依據V=Bδ^X-L可得殘差矩陣,而綜合變換法的原理就是對轉換后的殘差矩陣進行擬合。擬合是從數學原理來對數據的分析預估,可采用多項式擬合及曲面擬合等多種擬合方法,其中以最小多項式擬合最為常用。在實際應用中,更為重要的是對各種模型的比較,以便選擇一個最優模型,這里選用單位權方差估值的計算式作為擬合模型的選取準則。即
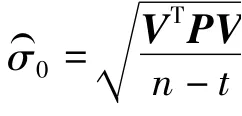
式中,n表示參加擬合計算的數值個數,t為擬合模型的參數個數。
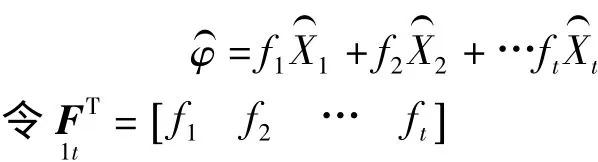
由協因數傳播定律知Q)x)x=(BTPB)-1
故 Q)φ)φ=FTQ)x)xF
5.九參數坐標轉換模型
傳統的七參數坐標轉換模型是單尺度模型,因此只需解算一個尺度參數即可。然而,GPS控制測量觀測的成果有高程方向上的誤差和平面坐標方向上的誤差,分別屬于兩個基準系統的數據,故尺度比并無可比性。因此GPS坐標轉換如果仍以單尺度模型進行坐標轉換,則不能很好地反映出兩坐標系統尺度上的差異。
因而將七參數轉換模型中尺度參數進行延伸,在X、Y、Z軸上各設置一個尺度參數是比較合理的,
這樣就得到九參數坐標轉換模型。
其中三尺度模型可表示為
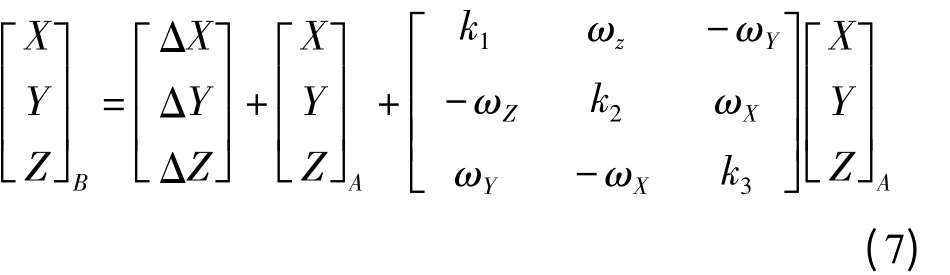
將其寫成誤差方程為
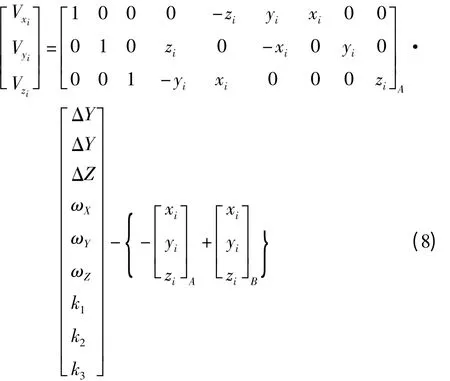
根據誤差方程式,按最小二乘法原理,即可求出兩坐標系之間的九轉換參數及坐標轉換精度。具有3個尺度參數的九參數模型其精度要比七參數模型的精度要高,更適用于小區域的GPS控制網的坐標轉換。
三、實例分析
如某測區面積約50 000 km2,5個已知重合點坐標見表1,分別為WGS-84和北京54坐標系下的坐標,依據上面建立的布爾薩模型及其延伸,求出相關的轉換模型,對兩種模型的精度進行比較(見表1)。
1.七參數坐標轉換模型
觀測數n=15,必要觀測數t=7,體系的自由度為15-7=8。
將表1中各點數據代入七參數的誤差方程中,依據δx=(BTPB)-1BTPL,(這里的權陣為單位陣)可求解出

式中,Δx0、Δy0、Δz0單位為m;ωΧ、ωY、ωZ單位為s。

表1 兩種模型精度比較

2.九參數坐標轉換模型
觀測數n=15,必要觀測數t=9,體系的自由度為15-9=6。
將表中各點數據代入九參數的誤差方程中,依據δx=(BTPB)-1BTPL,(這里的權陣為單位陣)可求解出

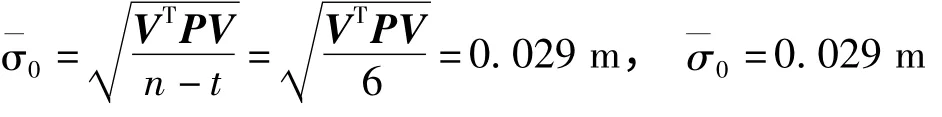
通過兩種模型精度的比較,可以看出九參數模型的單位權中誤差要小于七參數模型的單位權中誤差,由此,在小區域的GPS控制網中,采用九參數坐標轉換模型可以提高精度,減小誤差,且更適用于高差變化大的區域。針對控制測量面積的不同,其已知重合點的均勻性和密度應有不同的要求,如對于小區域的控制測量來說可寬松一些。
四、結束語
本文對一定區域GPS控制網的坐標轉換進行了研究,并結合布爾薩空間坐標轉換模型的原理及特點,將七參數坐標轉換模型進行了延伸,在相同原理的基礎上,演變成九參數坐標轉換模型,彌補了七參數坐標轉換模型中單一尺度的不足。研究成果對于測繪生產具有實際的應用價值和意義。
[1] 李成仁,岳東杰,袁豹,等.基于最小二乘配置的九參數模型在三維坐標轉換中的應用[J].測繪與空間地理信息,2014,37(7):193-196.
[2] 徐仕琪,張曉帆,周可法,等.關于利用七參數法進行WGS-84和BJ-54坐標轉換問題的探討[J],測繪與空間地理信息,2007,30(5):33-42.
[3] 孫小榮,張書畢,徐愛功,等.七參數坐標轉換模型的適用性分析[J].測繪科學,2012,37(6):37-39.
[4] 武漢大學測繪學院測量平差學科組.誤差理論與測量平差基礎[M].武漢:武漢大學出版社,2014.5.

