天文經緯度歸心實用算式推證

蘇明曉，包 歡，趙軍喜，王玉峰

（1．96633部隊，北京 100096；2．信息工程大學 地理空間信息學院，河南 鄭州450052；3．92292部隊，山東 青島 266405）

1 天文經緯度歸算至標志中心算式的推證

1．1 歸心計算式的推證過程

圖1中設C為測站，天文經緯度為λ0，φ0。Z為庫房測試間的地面標志中心，天文經度和緯度分別為λ，φ。歸心的目的是將測站天文經緯度歸算為標志中心的經緯度，需測定歸心元素：d為測站C到標志中心Z之間的水平距離，α為CZ方向的方位角，由正北起算。CK為C點的平行圈，在球面三角形CZK中有

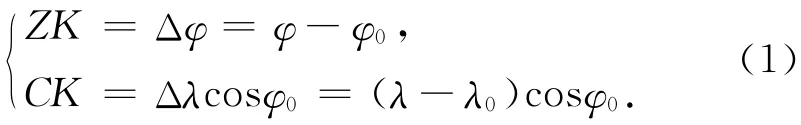
球面三角形CZK相對較小，可視作平面三角形，所以

圖1 測站歸心

因此

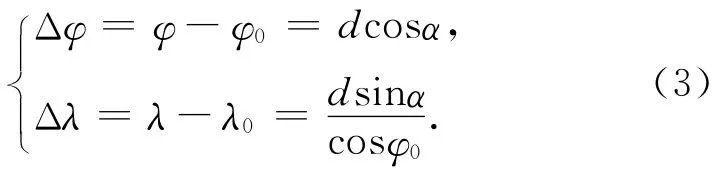
第一等式右邊應乘以ρ／M0，第二等式右邊應乘以ρ／N0，得到

其中ρ＝206 265是角秒與弧度的換算常數；M0和N0為C點的子午圈曲率半徑和卯酉圈曲率半徑。在橢球測量學中［2］

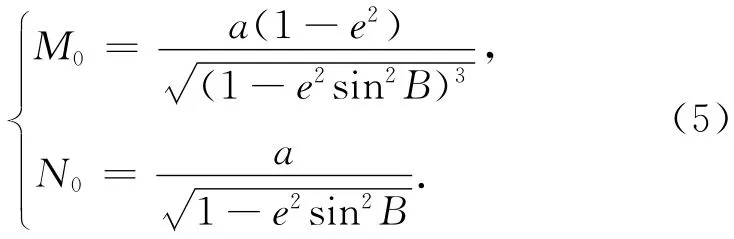
式（5）中a是參考橢球的長半軸，e2是由參考橢球基本元素導出的常數，B是測站點的大地緯度。于是得到精密的天文經緯度歸心計算式

然而，國際米原器的準確度只有0.1微米，并且難以復現，容易損壞，隨時間會有緩慢的變化。所以，隨著科學技術的發展，用自然米取代實物米就成為了一個必然趨勢。

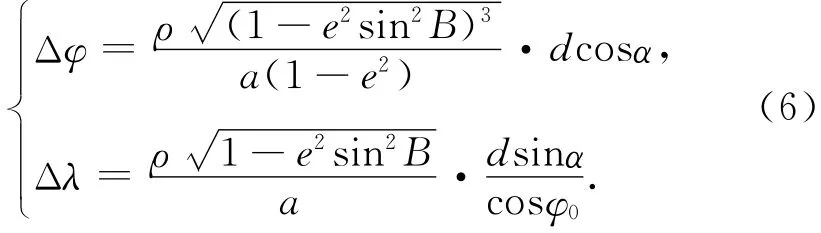
該式在一些文獻中存在不同形式的謬誤，數據處理人員在使用時務必注意。

由式（3）知測試間地面標志中心點的天文經緯度

1．2 天文經緯度歸心計算式中變量特點

分析式（6）中的變量：d，α和φ0是測站點的觀測數據，隨測站位置和實際條件而變化；ρ，a和e是（與參考橢球有關的）常數；B隨測站位置的變化而變化，影響歸心計算結果。在其它參數和變量確定不變的前提下，分析歸心元素d，α對歸心計算結果的影響：

1）d越大，Δφ和Δλ的絕對值也越大。

2）在α＝0°或180°時，cosα絕對值最大為1，Δφ的絕對值也最大；sinα絕對值最小，Δλ的絕對值也最小為0。

3）在α＝90°或270°時，cosα絕對值最小，Δφ的最小絕對值為0；sinα最大絕對值為1，Δλ的絕對值也最大。

2 天文經緯度歸心計算實用公式的設計

2．1 天文經緯度歸心計算實用公式的設計

我國自2008年7月1日起啟用2000國家大地坐標系，歸心計算使用的橢球參數是確定不變的［3－4］。不妨構建常數

我國領土的地理緯度大體在北緯3°～55°之間，隨著緯度B增大，sin B增大，（1－e2sin2B）減小，即常數Ⅰ和Ⅱ隨B增大而減小。為獲得有較好代表性的常數Ⅰ和Ⅱ的數值，分別取B＝3°和B＝55°，將2 000國家大地坐標系的橢球參數a＝6 378 137 m、常數e2＝0．006 694 380 022 9和ρ一并代入式（8）［5］；得到3°和55°處常數Ⅰ、Ⅱ的數值，取其均值作為常數Ⅰ、Ⅱ的結果［6］

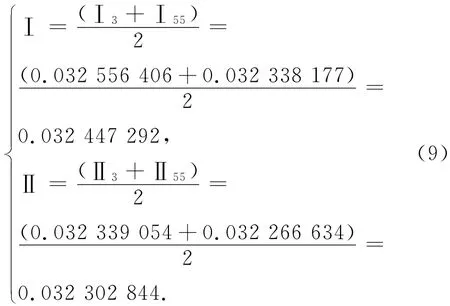
于是式（6）簡化為

這就是適于我國境內使用的天文經緯度歸心計算簡化公式。Δφ和Δλ計算結果的單位分別是角秒和時秒。

2．2 歸心元素測量精度的數學分析

式（10）中觀測值d和α相互獨立，其測量的中誤差為md和mα，根據誤差傳播定律，Δφ和Δλ的誤差mΔφ和mΔλ應為［7］

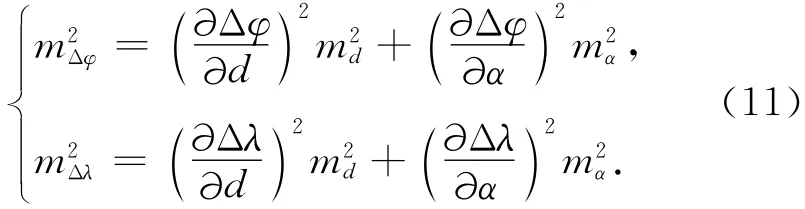
進一步計算偏導數

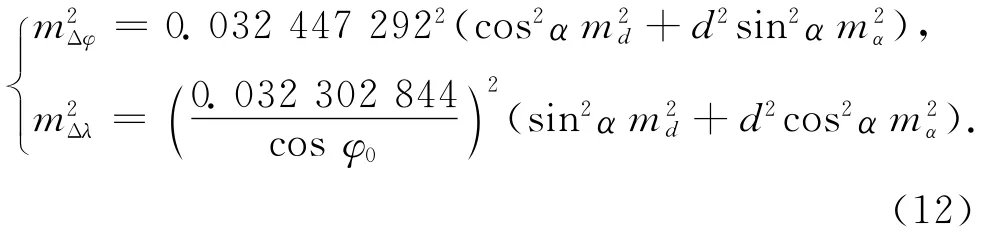
解得

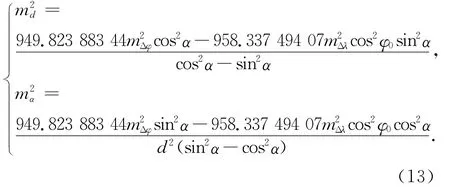
可見在Δφ和Δλ精度既定的情況下，歸心元素的測量精度與測站點天文緯度φ0有關，且隨偏心觀測的水平距離d和方位角α的大小不同而變化，具體作業時宜根據作業條件確定歸心元素的測量精度。

3 計算比對及結論

為分析歸心計算式的精度，對試驗數據做如下處理：

1）為保證公式的實用性，歸心元素d使用近年實際數據處理作業中遇到的最大值350 m；

2為便于討論，歸心元素α分別取接近其最大值的0．1°和89．9°各兩組數據；

3）大地緯度B分別取3°和55°各兩組數據，以確保試驗數據涵蓋我國境內大部分地區；

4）天文緯度φ0與大地緯度B取值基本一致。

在使用簡化天文經緯度歸心式（10）計算的同時，使用精密天文經緯度歸心式（6）進行比對計算。試驗數據及計算、比較和統計結果見表1（為方便比較，Δλ單位也用角秒表示）。

專用工程需要的天文緯度和經度測量中誤差分別是±0．5″和±0．4 s（相當于±0．6″）。

1）天文緯度和經度歸心簡化實用公式與精密公式計算結果最大互差分別是0．038″和0．022″，這種極值出現在我國疆域的南北兩端，且小于所需天文緯度和經度測量中誤差的10%。在我國中部廣大地區其互差僅為測量中誤差的1～2%。二者計算結果互差達到可以忽略的量級。

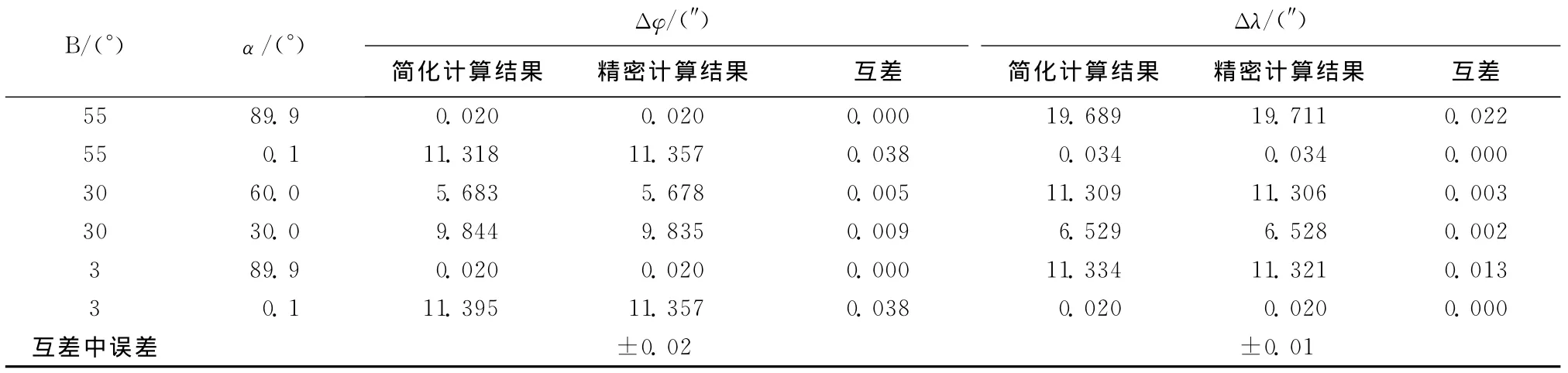
表1 兩種天文經緯度歸心計算結果比較表

2）天文緯經度歸心簡化實用公式與精密公式計算結果互差中誤差分別是±0．02″和±0．01″，均達不到天文緯度和經度測量中誤差的5%，忽略其差異不會對成果精度產生明顯影響［8］。

即用簡化天文經緯度歸心公式計算獲得的歸心改正數Δφ和Δλ精度與精密計算公式相當，該式完全可以用于設備庫房導航設備測試間的天文經緯度歸心數據處理。

利用簡化的天文經緯度歸心計算實用公式，可在野外簡陋環境下快速計算天文經緯度歸心改正數，獲取設備測試間地面標志中心點的天文經緯度；或作為歸心改正精密計算結果正確性的檢核手段，增強成果可靠性。

［1］ 艾貴斌．導彈陣地大地測量原理與方法［M］．北京：解放軍出版社，2011：432－439．

［2］ 郭群長，李仲勤，李輝．橢球大地測量學概論［M］．成都：西南交通大學出版社，2009：50－55．

［3］ 程鵬飛，成英燕，文漢江．2000國家大地坐標系實用寶典［M］．北京：測繪出版社，2010：127－128．

［4］ 田桂娥，宋利杰，尹利文，等．地方坐標系與CGCS2000坐標系轉換方法的研究［J］．測繪工程，2014，23（8）：66－69．

［5］ 呂志平，喬書波．大地測量學基礎［M］．北京：測繪出版社，2010：90－95．

［6］ 中國人民解放軍總裝備部．GJB 6304－2008 2000中國大地測量系統［S］．北京：總裝備部軍標出版發行部出版，2008．

［7］ 孔祥元，郭際明．控制測量學［M］．武漢：武漢大學出版社，2010：116－122．

［8］ 隋立芬，宋力杰，柴洪洲，等．誤差理論與測量平差基礎［M］．北京：測繪出版社，2010：40－45．