基于彈性薄板理論的采場頂板破斷特征分析
王新豐 高明中 陳雨雪 王建建 蘭學強 周安偉
(1.煤礦安全高效開采省部共建教育部重點實驗室,安徽 淮南232001;2.安徽理工大學能源與安全學院,安徽 淮南232001)
巖層活動與礦山壓力聯系密切,采場圍巖活動是形成礦山壓力的根源,礦山壓力的顯現也是采場圍巖活動的具體表現[1]。采礦界眾多學者針對采場頂板的破斷特征展開了大量研究[2-4],提出了以壓力拱、懸臂梁、鉸接巖梁、砌體梁及傳遞巖梁為主的多種巖梁假說。但巖梁理論未能凸顯巖層結構的空間概念,為了更加直觀獲取頂板破斷的宏觀特征,人們開始嘗試用薄板模型來揭示覆巖破斷的內在機理與空間形態[5-7],根據不同的支承邊界條件建立了采場礦壓薄板理論的力學模型,研究了工作面頂板結構破斷及裂紋發展的力學特征。然而由于前人對于薄板理論的應用研究大多選取某一特定的開采階段展開探討,因此很難全面獲取頂板不同時期的破斷特征。為了反映頂板破斷的連續性和時效性,本研究采用彈性薄板的小撓度理論構建不同開采階段下的頂板力學模型,從巖層運動的角度揭示頂板破斷的失穩機理。
1 頂板破斷的力學模型分析
采礦中形成的頂板由于其高長比很小可將其簡化為矩形薄板[7],根據采場頂板瞬時破壞、分段延伸和分區遷移的時空特點,對采場頂板構建四邊固支、兩邊固支兩邊簡支和四邊簡支3 種不同支承邊界條件下的力學模型,通過對3 種力學模型的分析求解,可以得到采場頂板不同破斷時期的力學演化形態。
1.1 頂板破斷前的力學模型分析
采場頂板破斷前可將其視為四邊固支的矩形薄板,采場覆巖受均布荷載q 作用。矩形頂板長為2a,寬為2b(其中b <a),板厚為h,彈性模量為E,泊松比為μ,抗彎剛度為D,板的撓度為ω,內力彎矩為Mx、My,頂板應力為σx、σy和τxy。建立四邊固支的矩形頂板力學模型,如圖1 所示。
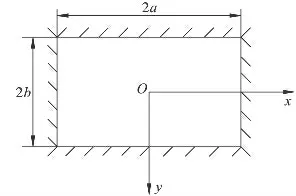
圖1 四邊固支頂板力學模型Fig.1 Mechanical model of the roof with four edges clamped
根據題設條件可知,該矩形薄板的邊界條件為
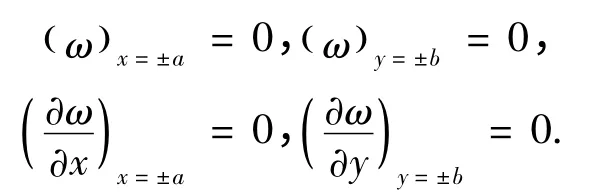
基于彈性力學的最小勢能原理,利用瑞利-里茨法[8]構建滿足邊界條件的一階撓曲面方程
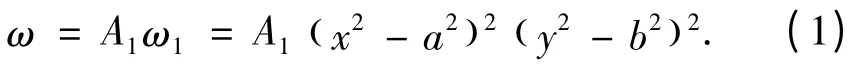
根據薄板彎曲的直法線假設,在不計應變分量的情況下,求得薄板彎曲的總勢能為
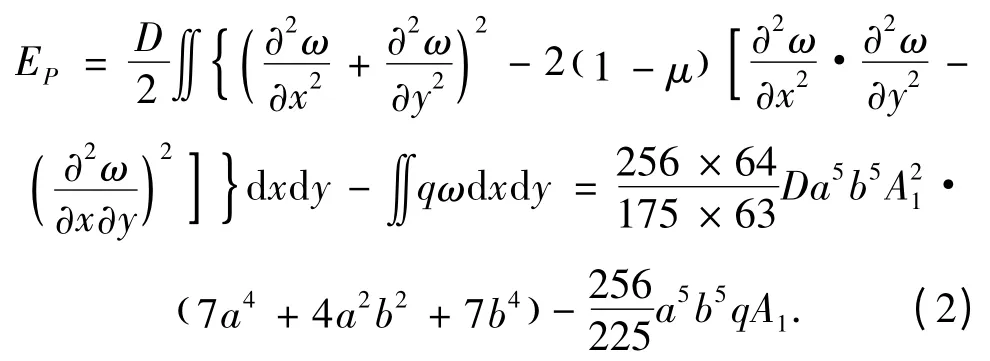
由(?EP)/(?A1)得
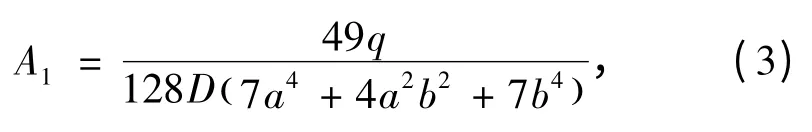
進而求得
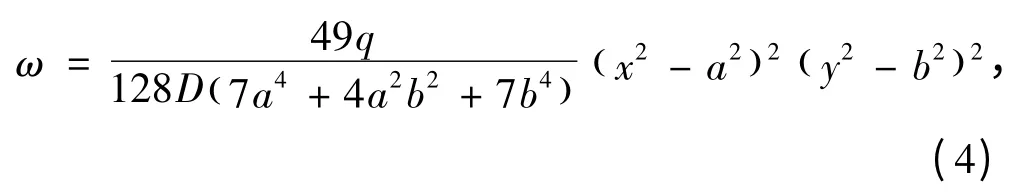
其中,
D = Eh3/[ 12 (1 - μ2)] .
根據彈性力學的內力彎矩公式[8],求得等厚薄板的彎矩為
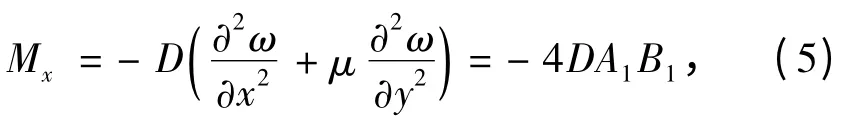
其中,
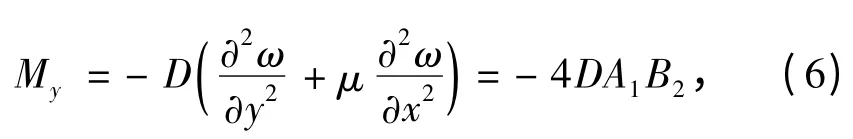
其中,
B1=[( y2-b2)2( 3x2-a2)+μ ( x2-a2)2( 3y2-b2)],
B2=[( x2-a2)2( 3y2-b2)+μ ( y2-b2)2( 3x2-a2)].
利用彈性力學的應力推導公式[8],求得等厚薄板的頂板應力為
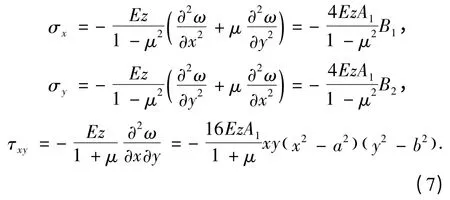
采用數學極限求導方法對彎矩式(5)、式(6)進行極值求解,可以得出矩形頂板的彎矩最大值點在長邊中點,即點(0,±b)處,此時對應的頂板應力相對較大。因此長邊中點處的彎矩值將首先達到巖體的極限彎矩開始發生破斷,破斷后的裂紋不斷向長邊兩端蔓延擴展,直至破壞到長邊邊緣。
1.2 頂板破斷期間的力學模型分析
矩形頂板的長邊破斷以后,采場頂板的固支長邊將變為簡支邊,進而構建頂板破壞期間兩邊固支兩邊簡支的力學模型,如圖2 所示。
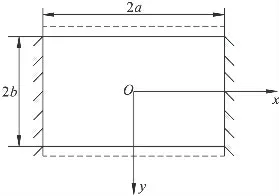
圖2 兩邊固支兩邊簡支的頂板力學模型Fig.2 Mechanical model of the roof with two edges clamped and two edges simple supported
由題設條件可得,該等厚薄板的邊界條件為
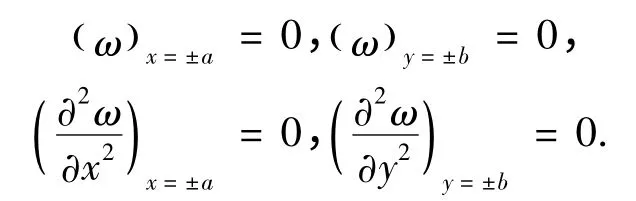
同樣利用瑞利-里茨法構建滿足邊界條件的一階撓曲面方程
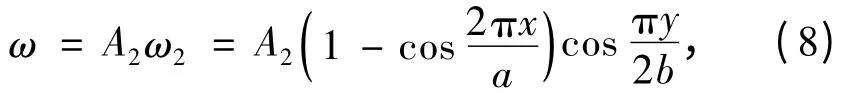
進而求得
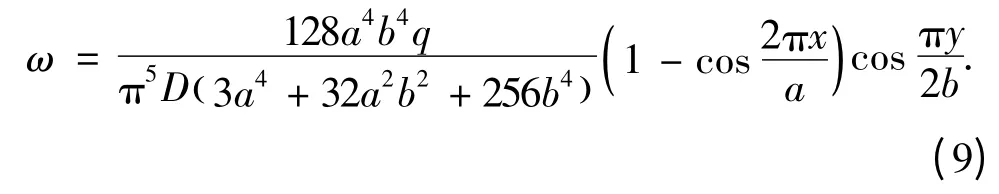
利用彈性力學的內力彎矩公式,求得等厚薄板的彎矩為
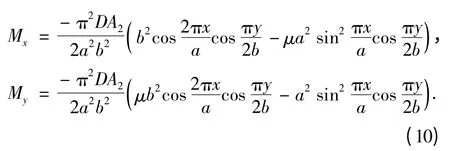
同樣對彎矩式(10)進行分析求解,得到頂板彎矩的最大值點在短邊中點,即點(±a,0)處,此時對應的頂板應力為
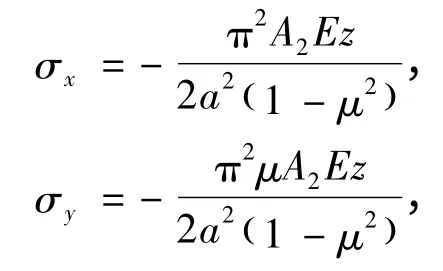
該力學模型下的矩形頂板首先在短邊中點附近達到其極限彎矩進而發生破斷,隨著開采的進行斷裂裂紋沿著短邊中點逐漸向兩端擴展,直至將短邊完全破斷,由原來的固支邊轉化為簡支邊,使得頂板內部形成環形破斷,近似為平面橫“O”型破壞。
1.3 頂板破斷后的力學模型分析
隨著工作面推進度的增加,當矩形頂板的四條固支邊全部破壞為簡支邊后,頂板破斷形式隨即改變,因此需重新構建力學模型,依據新的強度破壞準則進行力學求解,新建模型如圖3 所示。
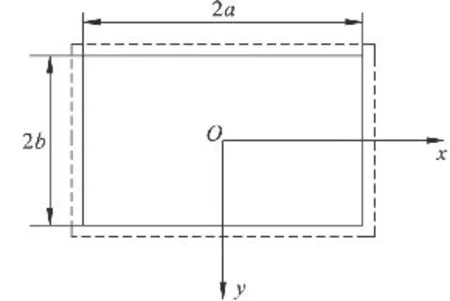
圖3 四邊簡支的頂板力學模型Fig.3 Mechanical model of the roof with four edges simple supported
依據題設條件,新建力學模型的邊界條件為
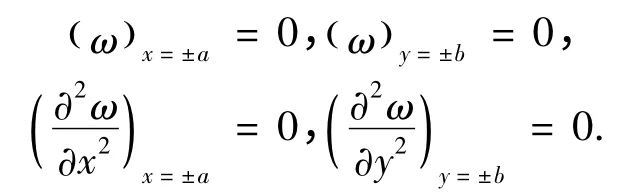
利用里茨法構建滿足上述邊界條件的一階撓曲面方程
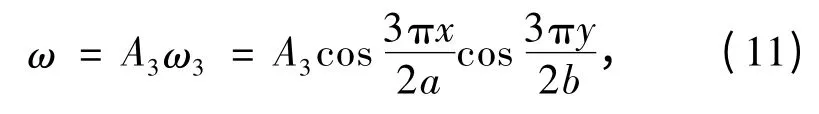
進而求得滿足條件的一階撓度表達式
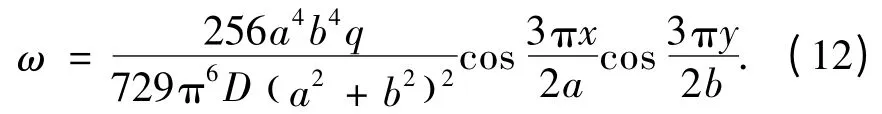
利用彈性力學的內力彎矩公式,求得等厚薄板的彎矩為
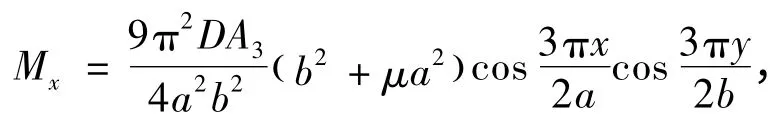
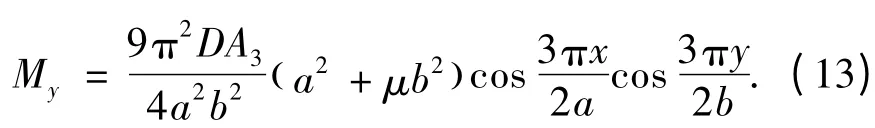
由彎矩式(13)可以求得頂板彎矩的最大值點位于矩形薄板的中心,即點(0,0)處,此時對應的頂板應力相對較大,因此該矩形頂板將在薄板的中心位置發生破斷,從而產生沿x 方向的橫向裂紋,且裂紋發展趨勢隨開采進度不斷向兩端擴展,并在短邊近端斷裂裂紋產生分叉,形成平面的橫“X”型破斷。
2 頂板破斷的力學特征
采場覆巖的破斷特征和垮落形態與開采進度和推進時間密切相關,表現為覆巖破壞的時空效應。通過對不同開采階段的頂板力學模型分析求解,可以得到頂板破斷的力學顯現特征和時空演變形態。采場頂板的破斷過程隨著開采活動的進行經歷了以下幾個演化階段:采動伊始,采場頂板首先在長邊中點發生破斷,破斷裂紋不斷向長邊兩端蔓延擴展,直至破壞到長邊邊緣;隨后矩形頂板的短邊中點開始破斷,并逐漸向兩端延展,促使薄板短邊完全破斷,斷裂裂紋與長邊端部交合貫通,構成環形破斷,形成平面的橫“O”型破壞;再隨著工作面繼續向前推進,頂板中心處發生破斷,產生沿x 軸方向的橫向裂紋并不斷向短邊擴展,最后在短邊近端斷裂裂紋發生分叉延伸,同薄板長邊的端角處交合貫通,形成空間的橫“X”型破斷。頂板四周形成的空間橫“O”型破斷與中部形成的“X”型破斷共同構成了頂板破斷的橫“O-X”型破壞形態,其頂板破斷的演化過程如圖4 所示。
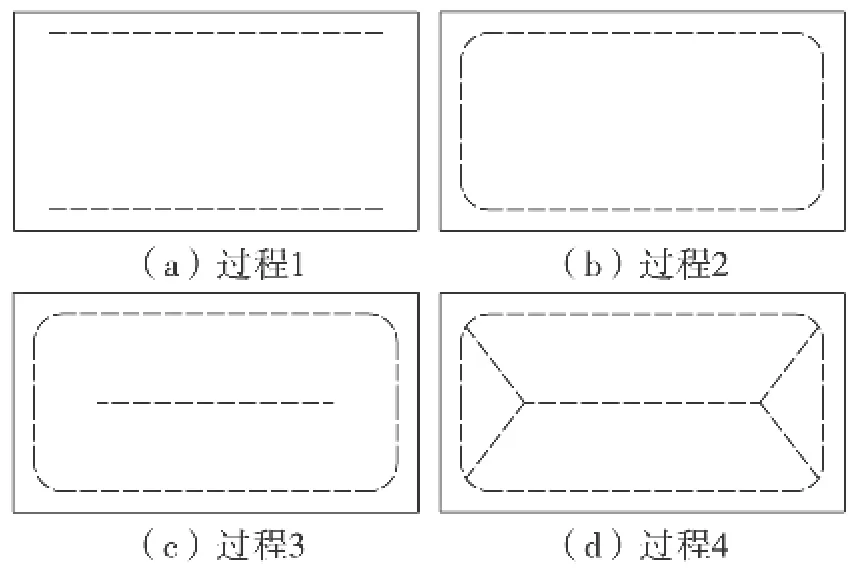
圖4 采場頂板橫“O-X”型破斷演化過程Fig.4 The evolutionary process of stope roof with horizontal "O-X "shape fracture
3 頂板應力演化規律的數值模擬
在理論分析采場頂板破斷規律的基礎上,運用三維數值模擬軟件FLAC3D對采場頂板的破斷過程進行建模分析。模型的幾何尺寸設計為600 m×400 m×200 m(長×寬×高),工作面斜長保持200 m 沿走向推進,推進期間為了避免邊界效應對模型開采的影響,走向兩邊各留100 m 的保護煤柱。煤層埋深約600 m,底板厚度45 m。模型四側和底部根據具體約束條件固定各邊界的水平方向位移或垂直方向位移,頂部定義為自由邊界并施加15 MPa 的均布荷載。
通過模擬煤層頂板應力場的演變過程,可以從宏觀上窺探頂板應力的分布狀態及時空演化規律(見圖5)。煤層開采至50 m(圖5(a))時,頂板長邊首先出現應力集中現象,長邊中部的應力顯現程度較高,應力峰值集中于長邊中點。工作面推進到100 m(圖5(b))時,短邊中部開始出現應力集中,且應力集中區域由短邊中心向端末發展。當工作面推進到150 m(圖5(c))以后,頂板中部應力開始顯現,并隨工作面推進度的增加不斷由中心位置向外輻射。隨著應力數值不斷增大,應力集中現象隨之擴展,工作面推進到300 m(圖5(f))時應力分布區域幾乎覆蓋了整個板面。綜合分析發現,應力集中出現的部位依次由“頂板長邊—短邊—中部”循序漸進地向前發展,頂板應力的宏觀演變特征與采場頂板的橫“O -X”型破斷較為吻合,其演變過程類似于頂板的橫“O -X”型破斷。
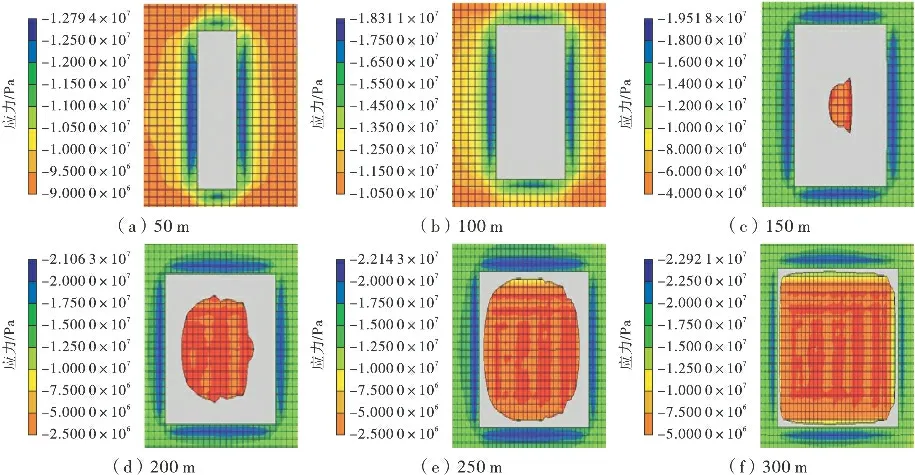
圖5 頂板應力的演化過程Fig.5 The evolutionary process of the roof stress
4 結 論
(1)針對煤層開采過程中采場覆巖形成的特定空間結構和變形破斷形態,運用彈性薄板小撓度理論構建了3 種不同支承邊界條件下的頂板力學模型,通過理論計算得出了頂板斷裂前后的撓度、彎矩和應力解析表達式,并從理論層面揭示了頂板破斷的力學特征,采場頂板首先在板邊四周形成平面的“O”型破斷,而后在中部形成平面的“X”型破斷,兩者交合貫通構成頂板的空間橫“O-X”型破斷。
(2)采用數值模擬軟件分析了頂板應力場的分布狀態和演化規律,工作面推進過程中頂板應力的集中部位依次由“頂板長邊—短邊—中部”逐漸向前擴展,其應力演變過程與頂板橫“O -X”型破斷相互印證。
[1] 張益東,程敬義,王曉溪,等. 大傾角仰(俯)采采場頂板破斷的薄板模型分析[J].采礦與安全工程學報,2010,27(4):487-493.
Zhang Yidong,Cheng Jingyi,Wang Xiaoxi,et al.Thin plate model analysis on roof break of up-dip or down-dip mining stope[J].Journal of Mining and Safety Engineering,2010,27(4):487-493.
[2] 史 紅,姜福興. 采場上覆大厚度堅硬巖層破斷規律的力學分析[J].巖石力學與工程學報,2004,23(18):3066-3069.
Shi Hong,Jiang Fuxing.Mechanical analysis of rupture regularity of hard and massive overlying strata of longwall face[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(18):3066-3069.
[3] 陳忠輝,謝和平,李全生.長壁工作面采場圍巖鉸接薄板組力學模型研究[J].煤炭學報,2005,30(2):172-176.
Chen Zhonghui,Xie Heping,Li Quansheng. Study on plate group mechanical model for main roof of longwall face[J].Journal of China Coal Society,2005,30(2):172-176.
[4] 錢鳴高,石平五.礦山壓力與巖層控制[M].徐州:中國礦業大學出版社,2003:66-70.
Qian Minggao,Shi Pingwu.Mining Pressure and Stata Control[M].Xuzhou:China University of Mining and Technology Press,2003:66-70.
[5] 賈喜榮,翟英達.采場薄板礦壓理論與實踐綜述[J]. 礦山壓力與頂板管理,1999,16(3/4):22-25.
Jia Xirong,Zhai Yingda.The review of groundpressure theory of thin slab in coal mining and its application[J]. Ground Pressure and Strata Control,1999,16(3/4):22-25.
[6] 顧 偉,張立亞,譚志祥,等. 基于彈性薄板模型的開放式充填頂板穩定性研究[J]. 采礦與安全工程學報,2013,30(6):886-891.
Gu Wei,Zhang Liya,Tan Zhixiang,et al. Study on roof stability of open backfilling based on elastic plate model[J].Journal of Mining and Safety Engineering,2013,30(6):886-891.
[7] 浦 海,黃耀光,陳榮華.采場頂板X -O 型斷裂形態力學分析[J].中國礦業大學學報,2011,40(6):835-840.
Pu Hai,Huang Yaoguang,Chen Ronghua.Mechanical analysis for XO type fracture morphology of stope roof[J]. Journal of China University of Mining and Technology,2011,40(6):835-840.
[8] 吳家龍.彈性力學[M].北京:高等教育出版社,2001.
Wu Jialong. Elasticity Mechanics[M]. Beijing:Higher Education Press,2001.

