基于LS-SVR 的光電式濁度傳感器研究

紀瑩蕾，陳 鋒

(中國科學技術大學 自動化系，安徽 合肥230026)

0 引 言

濁度反映的是水樣的一種光學特性，它體現為水中懸浮物和膠體物質等對光線透過水樣時所產生的阻礙程度，濁度的測量方法很多，常見的是透射法和90°散射法。透射法不適合測量低濁度，因為低濁度時，入射光基本上都直接透射過去，很難檢測細微的濁度變化;散射法不適合測量高濁度，因為高濁度下粒子會產生重復散射，使得散射光強快速衰減，濁度和散射光強的線性度變差;比值法是利用散射和透射的比值與濁度的線性關系得到濁度值，它可以減小光源和色度的干擾，但是該線性關系只適用于一定濁度范圍［1］。在散射法基礎上，Dana D R［2］等人提出利用后向散射檢測來改進濁度測量范圍;宋啟敏等人［3］則證明30°前向散射檢測可以增大濁度檢測范圍，同時改善非線性度;Kunio Ebiea 等人［4］提出在前向散射的基礎上，采用雙光束探測來減小光源干擾，提高濁度檢測精度。這三種方法雖然提高了測量精度，擴大測量范圍同時改善線性度，但都需要額外增加光學器件，增加光路設計復雜性。

本文提出了一種濁度檢測的改進方法。首先，綜合散射、透射、比值三種數據檢測結果，利用散射法來降低低濁度誤差，利用透射法來降低高濁度誤差，利用比值法進行線性補償和抗光源干擾;其次，加入環境光采集裝置和溫度裝置消除背景光和溫度影響;最后，利用最小二乘支持向量回歸(LS－SVR)對透射、散射、比值、溫度、環境光進行數據融合，在合適的范圍內選擇合適的權重，綜合這三種方法的優點以獲得濁度測量值，提高濁度檢測的精度和抗干擾能力。

1 相關理論

1.1 透射法原理

透射法的公式如下

其中，Il為透射光強，lx;A 為電路常數;Io為入射光強，lx;k 為與入射光波長與微粒分布等相關的常數;T 為水樣濁 度，NTU;L為透射光程，mm。由公式(1)可以看出濁度的大小和透射光強對數值呈單調衰減的關系。

1.2 散射法原理

當水中懸浮顆粒直徑小于入射光波長時，散射法滿足瑞利散射定理;當水中懸浮顆粒直徑大于入射光波長時，散射法滿足米氏散射定律。雖然滿足的定理與波長有關，但是相關公式可以簡化為

其中，Ks為與散射相關的比例系數;Is為散射光強，lx。由公式(2)可知，散射光強度與濁度呈正比關系。

1.3 比值法原理

理想情況下，散射光強與濁度呈線性關系，但是散射光在到達光電接收器之前，會因為穿過一定光程的水樣而發生衰減。將衰減后的散射光強與透射光強進行比值處理，公式如下

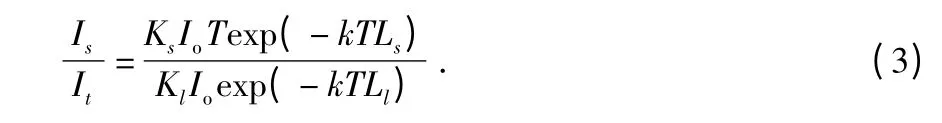
如果設計中將透射光程Ll和散射光程Ls設置相同，就可以得到濁度與光強比值之間的線性關系。

2 基于LS-SVR 的濁度檢測建模

LS－SVR 適宜解決非線性和小樣本的問題，且學習能力強，泛化性能好［5］。由于濁度檢測的三種方法各自適用的線性范圍不同，超出相應的線性范圍就會出現非線性現象，并且檢測過程中存在溫度和環境光干擾，這些干擾會影響到檢測值精度。同時濁度標定過程中，樣本點較少，因此，本文利用LS－SVR 濁度檢測建模來提高檢測精度穩定性。

2.1 LS－SVR 算法

給定訓練樣本集(xk，yk)，k=1，2，…，m，xk∈Rn，yk∈R。根據公式(4)來對樣本進行擬合

其中，φ(x)為從低維特征空間到高維的非線性映射。考慮到擬合誤差和函數復雜度這2 個因素，利用結構風險最小原則，可將回歸問題重新表述為帶約束的優化問題［6］，如公式(5)所示

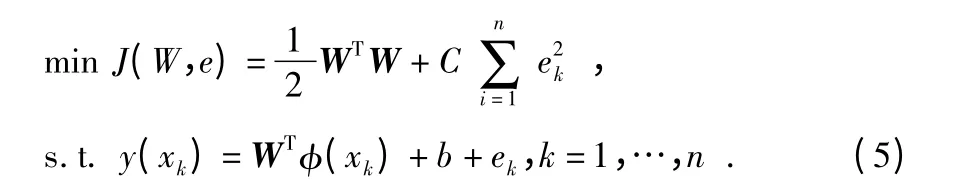
其中，ek為誤差，C 為調節因子，控制誤差的比重。通常，φ(x)的功能由核函數來進行取代，使用核函數可以減小內積空間計算，避開高維災難。常見的核函數有多項式核、線性核和高斯核，本文選用的核函數是高斯核函數，該核函數靈活性很大，應用比較廣泛，其公式如下

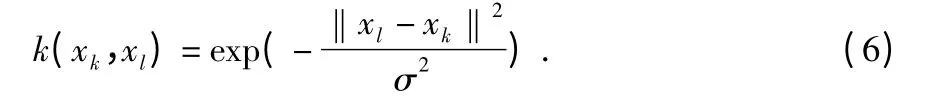
對于高斯核函數，參數σ 的選擇對分類效果影響比較明顯，當σ 趨近于零的時候，所有的訓練樣本點都作為支持向量，這就產生“過學習”現象，容易錯誤識別樣本點，推廣能力較弱;反之，如果σ 趨近于無窮，則所有樣本的地位相同，推廣能力和對測試樣本的正確判斷能力都為零，也就是所有樣本都是同一類。

2.2 濁度建模

散射法測濁度時，散射電壓與濁度大小為線性關系，但是這種線性關系只適用于低濃度(0 ～40 NTU)狀態［7］。當濃度升高時，由于重復散射現象的發生導致采集到的散射光強衰減，散射電壓值與濁度值呈現一種非線性關系。透射電壓值與濁度大小呈對數線性關系。因此，本文首先對透射電壓取對數處理，再利用透射電壓對數值和濁度大小進行擬合。但是，這種對數線性關系只在中高濃度有效。濃度過低時，入射光強基本穿過待測液體，由微粒透射產生的細小變化很難被感知到。比值法建立在散射和透射基礎上，它能夠減小光源的干擾，但是濁度和比值的線性關系只適用于一定的范圍。此外，溫度和環境光也會對濁度的測量產生影響。溫度升高時，光源的輻射功率降低，光電探測器的分流電阻減小，從而導致檢測到的散射值和透射值減小。環境光，指的是并非由入射光被水樣中的顆粒散射而產生的光，它被探測器檢測到時同樣會產生干擾。根據以上分析，本文建立基于LS－SVR 濁度檢測模型，如圖1 所示。

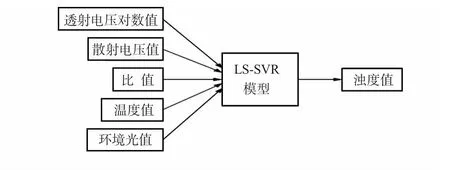
圖1 基于LS-SVR 濁度檢測模型Fig 1 Turbidity measurement model based on LS-SVR

圖1 中，輸入因子包括散射電壓值、透射電壓對數值、散射和透射的電壓比值、溫度值和環境光值;采用的算法是LS－SVR;輸出因子即是濁度值。本文首先通過實驗標定得到訓練數據，然后將訓練數據輸入模型中，調節參數σ 和C，控制支持向量的個數和誤差的比重，得到訓練時間和擬合誤差綜合較好的LS－SVR 模型。最后利用既得模型，求出濁度值。

3 實 驗

3.1 系統結構

本系統結構框圖如圖2 所示。其中，供電單元提供系統需要的+5 V 直流電。光源發出的光穿透盛放待測溶液的比色皿后，被探測器接收。探測器將接收到的光信號轉變為電信號，通過信號調理電路進行提取和放大，利用A/D采樣將模擬信號轉換為數字信號輸入微處理器。溫度芯片和光照芯片將采集到的溫度和環境光傳入微處理器，微處理器對散射值、透射值、散射和透射的比值、溫度值以及光照值進行數據融合，從而獲得濁度檢測值。

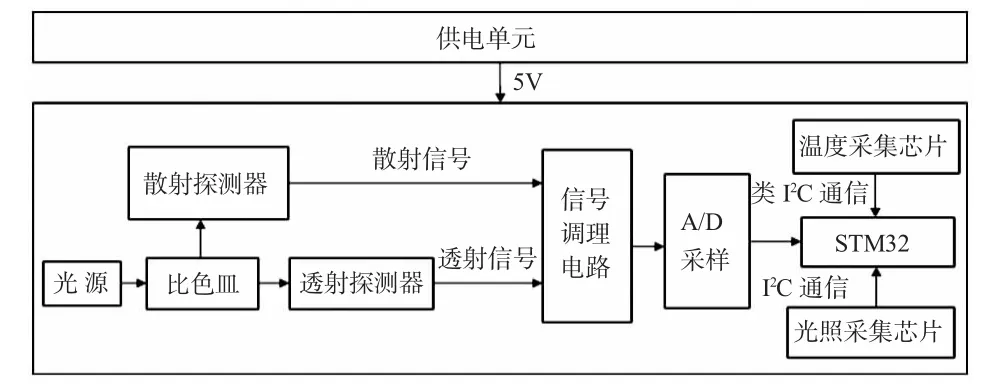
圖2 系統結構框圖Fig 2 Block diagram of system structure

3.2 實驗對比分析

為了精確測量濁度大小，本文將標準400 NTU 的福爾馬肼濁度液稀釋為14 個梯度，10 個梯度用來作為訓練數據，剩下梯度用來對實驗結果進行驗證。訓練完畢后，利用訓練獲得的參數對驗證數據進行擬合。

本文將檢測到的數據訓練后，利用本文方法對4 個梯度進行驗證，并將其與常見的三種方法進行比較。根據實驗結果計算得到，散射LS－SVR 誤差平均值為9.5%;透射LS－SVR 為12.4%;比值LS－SVR 為3.6%;而使用本文方法得到的誤差是2.7%，誤差遠遠小于以上三者的誤差，它們的誤差分布趨勢見圖3。可見，綜合三種方法的LS－SVR 能夠有效改善測量精度。

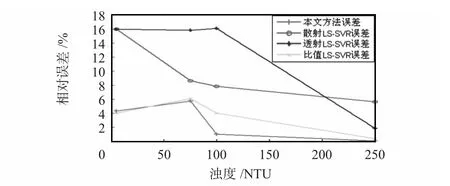
圖3 誤差對比Fig 3 Error comparison

3.3 實驗干擾性分析

干擾因素主要指的是溫度和環境光干擾。為了更好地研究溫度和光照對濁度的影響，按照控制變量法，在分析溫度干擾時，通過調節密封裝置使得光照強度維持在1 lx 左右，溫度的干擾比對結果如表1 所示。同理，在分析光照干擾時，將溫度維持在室溫環境下，大約25 ℃左右;由于本文在濁度檢測中加入避光罩，因此，進入濁度傳感器的光線很少，故考慮光強為150 lx 以內外界光對濁度值的影響，環境光的干擾比對結果如表2 所示。

由表1 可知，溫度對濁度的影響是存在的。本文以25℃為參考標準，當偏離常溫25℃后，隨著溫度的偏離程度越高，誤差也就越大。加入溫度因素后，能夠有效降低濁度檢測誤差。由表2 可以看出:外界環境光使得濁度檢測值偏大，隨著光照的增加，濁度檢測的偏差也越來越大。加入光照因素后，能夠減小濁度檢測誤差。

表1 15 ～35 ℃環境溫度干擾測量結果Tab 1 Measurement result of 15 ～35 ℃temperature environmental interference

表2 1 ～116 lx 環境光干擾測量結果Tab 2 Measurement result of 1 ～116 lx ambient light interference

4 結束語

本文分析了濁度常見的測量方法，針對散射法適合測量低濁度，透射法適合測量中高濁度和比值法能減小光源干擾的特性，利用LS－SVR 將三者進行融合，選擇最佳濁度預測值，從而提高了檢測精度。同時，為了增強濁度檢測的抗干擾性，在濁度傳感器設計中加入環境和溫度檢測裝置，并將二者加入濁度模型中。實驗結果證實:本文的設計方法能夠提高濁度檢測精度，改善濁度測量儀性能，增強其穩定性。

［1］ 張 愷，張玉鈞，殷高方，等.綜合散射法與透射法測量水濁度的研究［J］.大氣與環境光學學報，2011，6(2):100－105.

［2］ Dana D R，Maffione R A.Determining the backward scattering coefficient with fixed－angle backscattering sensors－revisited［C］∥Ocean Optics XVI，Santa Fe，New Mexico，US，2002:18－22.

［3］ 宋啟敏，陸明剛.散射光式濁度測量的范圍和非線性研究［J］.上海大學學報:自然科學版，1997，3(5):564－569.

［4］ Kunio Ebiea，Dabide Yamaguchia，Hiroshi Hoshikawab，et al.New measurement principle and basic performance of high－sensitivity turbidimeter with two optical systems inseries［J］.Water Research，2006，40:683－691.

［5］ Yan Weiwu，Shao Huihe.Application of support vector machines and least squares support vector machines to heart disease diagnosis［J］.Control and Decision，2003，18(3):358－360.

［6］ Suykens J A K，Vandewalle J.Least squares support vector machine classifiers［J］.Neural Processing Letters，1999，9(3):293－300.

［7］ ISO 7027.Water quality－determination of turbidity［S］.International Organization for Standardization(ISO)，1999.