基于傳感器的細長體橫向低頻振動載荷辨識*

吳巧瑞，姚熊亮，孫龍泉

(哈爾濱工程大學 船舶工程學院，黑龍江 哈爾濱150001)

0 引 言

細長體的水下發射有垂直發射和水平發射，相對而言，垂直發射具有貯彈量大、發射率高、可以全方位發射、反應時間短、可以對目標實行飽和攻擊等的顯著優點［1］。細長體的出水過程可分為三個階段:細長體出筒段、水中自由航行段和穿越水面段［2］。雖然這個過程一般只持續幾秒鐘，但細長體卻經歷了一系列復雜的運動環境，具體表現為高動壓、非定常和多相流動。

在細長體出筒過程中，筒內燃氣會隨著細長體尾部從筒內溢出，并與周圍的水摻混，在此過程中，水氣之間傳遞動量和能量，導致水氣混合物的壓力不斷震蕩，同時形成尾空泡［3］和肩空泡［4］。尾部氣泡和肩部空泡隨著細長體出水會發生坍塌，對細長體表面產生很大的沖擊力。水中自由航行階段，細長體將承受風、浪、流復雜海洋環境載荷;在穿越水面階段，自由液面會沿著高速運行的細長體表面上升，到達一定高度后脫落并對沖擊細長體表面。由此可見細長體在出水過程中將遭受十分復雜的載荷作用。

細長體在非定常非均勻載荷作用將發生橫向振動，其中，低頻振動具有振動能量大、結構響應位移大和變形大的特性［5］，因此，它可能會造成極大的危害。另外，由于細長體承載能力較差。因此，對細長體橫向低頻振動載荷的辨識具有很大的必要性。

本文在模態疊加法的基礎上，開發了一種辨識細長體在出水過程中橫向低頻振動載荷的方法，即根據細長體發射試驗中傳感器測得的加速度等信息，辨識細長體出水過程中的低階振動受力狀態，即彎矩和剪力信息，并判斷最大載荷出現的細長體截面，為細長體結構的強度校核和結構設計提供依據。

1 低頻振動載荷辨識方法

1.1 載荷辨識理論推導

細長體結構的運動方程可離散成多自由度系統的運動方程式

式中 Ms為結構的質量矩陣;Cs為結構的內阻尼矩陣;Ks為結構的剛度矩陣;L 為流體力(包括外力和結構運動引起的水動力)節點矢量;ω 為結構的節點位移矢量，是時間和空間的函數，可寫成ω(x，t)。

結構在真空中的無阻尼自由振動方程式為

解之，可得其固有頻率λ01，λ02，…和干模態φ1，φ2，…用最初n 個干模態組成的模態矢量陣進行坐標轉換，則位移和廣義位移可寫成式(3)的形式

式中 φ=［φ1，φ1，…，φn］，q 為廣義坐標矢量，即結構在真空中的主坐標矢量。

另外，有

式中 M 為細長體各截面彎矩，正是本軟件要辨識的物理量，如果想得到細長體各截面的彎矩信息，必須知道細長體各階主坐標。由式(3)可得

式中 細長體各點加速度¨ω 是已經測得的加速度信息。下面將介紹如何根據各點加速度¨ω 進行辨識得到細長體各階主坐標qi(t)，進而得到細長體各截面彎矩M(x，t)和剪力N(x，t)。

細長體作為無限自由度的彈性振動系統，總體彈性振動和局部彈性振動疊加在一起。采用濾波技術將加速度的低頻部分和高頻部分分開，總體彈性振動和局部彈性振動分開。得到細長體的前幾階振動疊加的加速度¨ω 信息之后，再利用式(5)提取出各階主坐標。

經濾波后，式(5)可改寫成

利用式(6)提取主坐標各階主坐標qi(t)的傳統做法是直接將式(6)二次積分，但隨著積分時間步的延長，這種做法會使累計誤差越來越大，使積分出的位移ω1和主坐標產生qi(t)漫漂現象，即偏離實際值越來越遠。因此，本文采用拉普拉斯變換的方式求解式(6)，可有效地改善該現象。

對式(6)兩邊同時乘φi(x)并沿細長體長度方向上積分，可得

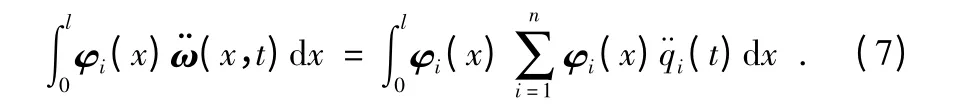
由于振型φ 具有正交性，易知

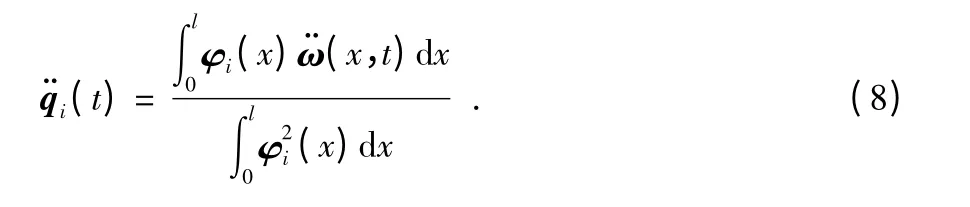
對式(8)兩邊同時做拉普拉斯變換

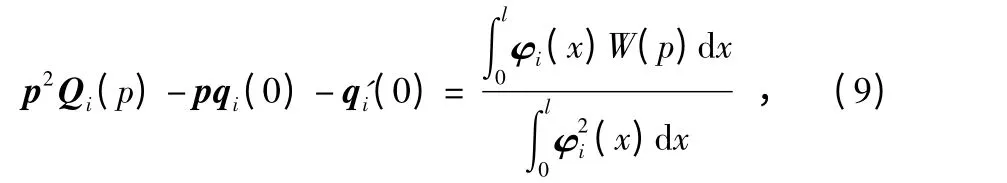
式中 Qi為qi(t)的拉普拉斯變換，易知

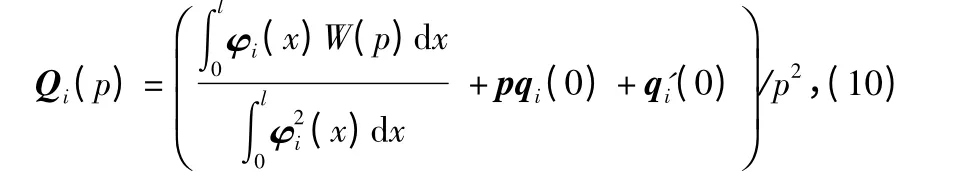
式中 q(0)和q'(0)可通過初始條件ω(0)，ω'(0)以及式(3)得到。

通過式(10)，求得Qi(p)后，對其進行反演即可得，而后通過式(4)即可得各截面彎矩

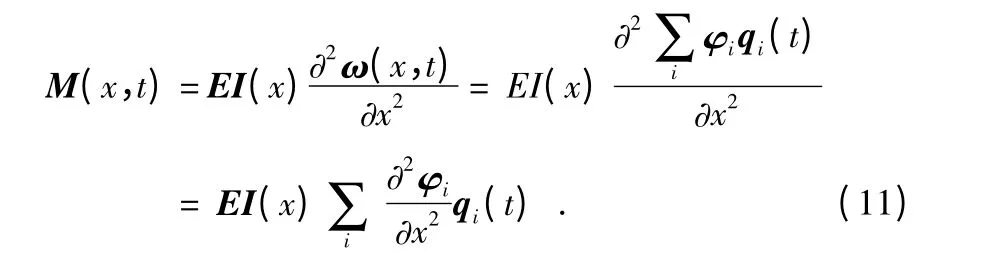
同理，可得各截面的剪力為

1.2 載荷辨識流程

由于本文目的是辨識細長體出水過程中低頻振動載荷，因此，在細長體出水實驗中，由位移傳感器測得細長體截面初始位移信息，速度傳感器測得初始速度信息和加速度傳感器獲得加速度信息。首先，要對測得的加速度信息進行濾波處理，濾去高頻部分，保留低頻部分。然后，即可使用1.1 節中的辨識方法得到任意截面的彎矩和剪力信息。另外，由于式(11)和式(12)中涉及高階導數求導問題，為了減小誤差，可以對φ 進行曲線擬合后求導。具體辨識流程如圖1 所示。

圖1 載荷辨識流程圖Fig 1 Flow chart of load identification

2 方法驗證

由于細長體出水數據的保密性，特選取一個具有解析解的模型算例［6］:如圖2 所示的一等截面簡支梁，其單位長度的質量為m，在1/4 跨長處作用一干擾力P0sin θt，并且θ=0.75ω1，已知阻尼比為ζ1=ζ2=0.05，用振型分解法求其位移和彎矩。

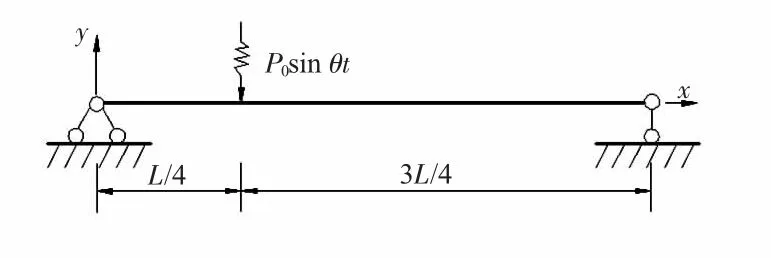
圖2 模型圖Fig 2 Modal illustration

由振型分解法，得彎矩和剪力的解析解分別為

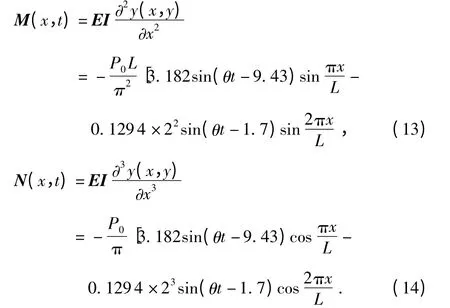
取彈性模量E=2.1×1011Pa，單位長度質量m=245 kg/m，慣性矩I=1.57×10－4m4，載荷幅值P0=1000 N，簡支梁長度L=2 m，計算步長 為0.000 05 s，計算時間為0.01 ～0.02 s。將相關的若干截面的初始速度信息、初始位移信息、加速度時歷值以及振型信息輸入程序，即可獲得任意截面的彎矩和剪力信息。

然后給出了x=1.0 m 和x=1.5 m 處使用本文提出的辨識方法所得的彎矩和剪力時歷曲線，并與解析解進行了對比，如圖3 和圖4 所示。在圖3 的彎矩比較圖中，解析解與數值解幾乎吻合，從局部放大圖中才能看出微小的誤差。在圖4 中，解析解和計算值也吻合較好，但顯然，其誤差要大于彎矩的計算誤差，這可能是剪力需要更高階的求導導致的。

3 結 論

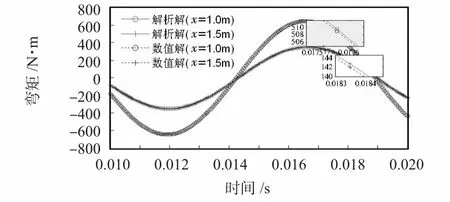
圖3 彎矩比較圖Fig 3 Comparison of moment

圖4 剪力比較圖Fig 4 Comparison of shear force

本文基于模態疊加法，提出了一種細長體出水橫向低頻振動載荷辨識的方法。在輸入傳感器測得相關的試驗數據的基礎上，對加速度進行濾波處理，濾去高頻部分保留低頻成分，可有效地辨識細長體出水過程中發生橫向低頻振動時，任意截面在任何時刻的彎矩和剪力信息，旨在判斷最大載荷截面以進行強度校核，為實際工程的結構設計提供一定的依據。

［1］ 裴 繯，張宇文，袁緒龍，等.潛載細長體垂直發射橫向振動特性仿真分析［J］.兵工學報，2009，30(8):1056－1060.

［2］ 申麗輝.航行體水下及出水過程的流體特性研究［D］.哈爾濱:哈爾濱工程大學，2013:1－8.

［3］ 劉志勇，顏 開，王寶獸.潛射細長體尾空泡從生成到拉斷過程的數值模擬［J］.船舶力學，2005，9(1):43－50.

［4］ 劉海軍，王 聰，鄒振祝，等.潛射細長體出筒過程肩空泡形態和水阻動力特性研究［J］.工程力學，2012，29(7):313－319.

［5］ 夏益霖，吳家駒.航天發射的低頻振動環境及其模擬［J］.強度與環境，1998(1):1－8.

［6］ 張相庭，王志培，黃本才，等.結構振動力學［M］.上海:同濟大學出版社，2005:112－117.