基于ABAQUS 的復合薄膜熱結構有限元分析

楊曉丹

(江蘇大學 機械工程學院，江蘇 鎮江212013)

0 引 言

三軸加速度傳感器是汽車電子和消費類電子產品市場發展的一個重要方向，有著巨大的市場份額。目前，娛樂系列消費類電子產品(如iPod，iPhone，SonyPS3，Wii 等)都應用了加速度傳感器作為動作操控和接收裝置。在Wii 和PS3 中，加速度傳感器可以靈敏地感測游戲者的動作，并將其轉換為游戲中的虛擬人物、物品或交通工具的動作和狀態等，并顯示在畫面中。iPod 和iPhone 中的加速度傳感器則可以根據用戶的動作而相應地對菜單進行操作。加速度傳感器在飛機導航系統中廣泛應用，它對GPS 衛星信號實現定位，配合陀螺儀或電子羅盤等元件一起可創建方位推算系統，對GPS 系統實現互補性應用。此外，三軸加速度傳感器在硬盤抗沖擊防護、子計步器和數碼相機的防抖等方面也得到了應用。

本文以熱對流［3，4］三軸加速度傳感器為研究對象，在已取得的研究成果基礎上，針對器件設計和制造中所涉及的關鍵問題展開研究，重點分析多層復合半導體薄膜懸臂梁在溫度場和應力場以及二者的耦合場作用下的形變機制。

1 有限元模型的建立與關鍵技術的研究

1.1 基本假設

基于有限元基于ABAQUS的半導體硅基復合薄膜彎曲懸臂梁熱結構分析是一個復雜過程，因此，對該過程進行數值模擬分析時，有必要做出某些近似和假設。在做熱結構分析的過程中，對彎曲懸臂梁撓度變化進行研究時，應做以下兩點基本假設［5］:

1)多晶硅腔壁絕熱，器件各部分的材料勻質且各向同性;

2)空氣與低應力Si3N4和SiO2薄膜的熱交換系數為一固定值。

1.2 半導體硅基復合薄膜彎曲懸臂梁模型的建立

半導體硅基復合薄膜彎曲懸臂梁的三維有限元是在ABAQUS/Explicit 軟件平臺上建立的，有限元模型參數是根據設計實體器件所提供的數據簡化而來，有限元模型如圖1所示(圖中上蓋已經被隱藏，這樣可以顯示內部結構，且垂直于腔體平面向上的為Z 軸正方向)。

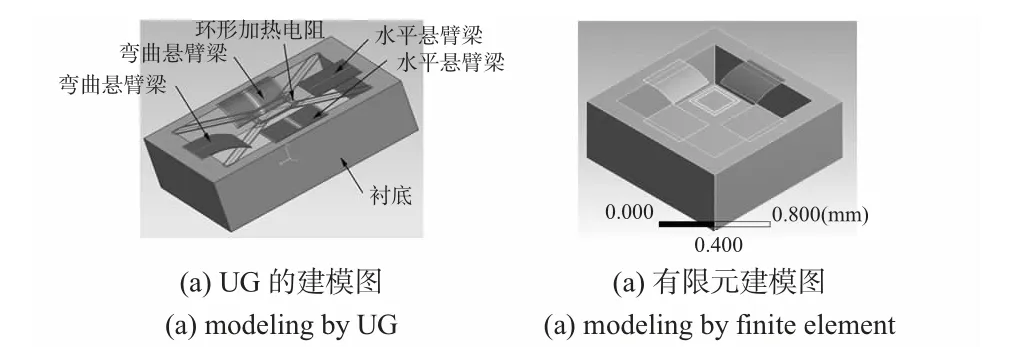
圖1 Z 軸測試腔的模型圖Fig 1 Model of Z axis test chamber

1.3 材料屬性的定義與網格劃分及邊界條件的定義

腔體材料是多晶硅，用來固定懸臂梁一端和保溫絕熱，不參與結果討論，所以，將它定義為剛體。雙層懸臂梁的下層是Si3N4［6］，楊氏模量E1=226 GPa，密度ρ1=3.44×103kg/m3，泊松比γ1=0.24，與空氣的熱交換系數h1=0.01 W/(m·K)，熱膨脹系數α1=2.1×10－6/K，比熱C1=0.71 J/(g·K)，懸臂梁的上層是SiO2，楊氏模量E2=75 GPa，密度ρ2=2.2×103kg/m3，泊松比γ2=0.17，與空氣的熱交換系數h2=0.02 W/(m·K)，熱膨脹系數α2=0.5×10－6/K，比熱C2=0.966 J/(g·K)，腔體中的填充氣體為空氣，密度為ρ2=1.29 kg/m3，對流換熱系數為h2=0.025 W/(m·K)。

網格劃分是通過布置種子來控制網格密度的，種子的近似全局尺寸設置為0.01，網格的單元屬性設置為六面體，劃分技術為結構化網格劃分，設定算法為中性軸算法，有限元模型網格劃分如圖2 所示。仿真模型中各個部件的接觸均定義為無摩擦面接觸。

1.4 分析步的定義和載荷定義

圖2 有限元模型的網格劃分Fig 2 Mesh of finite element model

在實際工作中，水平懸臂梁兩端是被固定的，在Z 軸方向上不會發生撓度變形，所以，不作討論。彎曲懸臂梁的一端被固定在腔壁中，所有方向的自由度被限制住，另一端自由，當彎曲懸臂梁受物理場作用時，需要考慮彎曲懸臂梁的撓度情況。當物理場作用在懸臂梁上時，要在相應的分析步中加載對應的物理量，比如:當有加速度作用在懸臂梁上時，需要在加速度分析步中加載加速度;當溫度場作用在懸臂梁上時，需要在溫度分析步中加載溫度;當加速度和溫度場的耦合場一同作用在懸臂梁上時，則需要在加速度分析步和溫度分析步中分別加載加速度和溫度，便可得到作用在懸臂梁上的耦合物理場。

2 有限元模擬分析

2.1 加速度場對復合薄膜彎曲懸臂梁撓度的影響

2.1.1 Z 軸負方向加速度對彎曲懸臂梁撓度的影響

有限元模擬條件:由于模型中的空氣、腔體和加熱器不參加計算，所以，新建了一個只有懸臂梁的簡易模型，用來加載加速度，模型的尺寸單位為mm。加速度分別取20，40，60，80 gn。方向沿Z 軸負方向，從后處理中得出相對位移的變化，再考慮初始撓度的大小，從而求得彎曲懸臂梁的實際撓度，如圖3 所示。

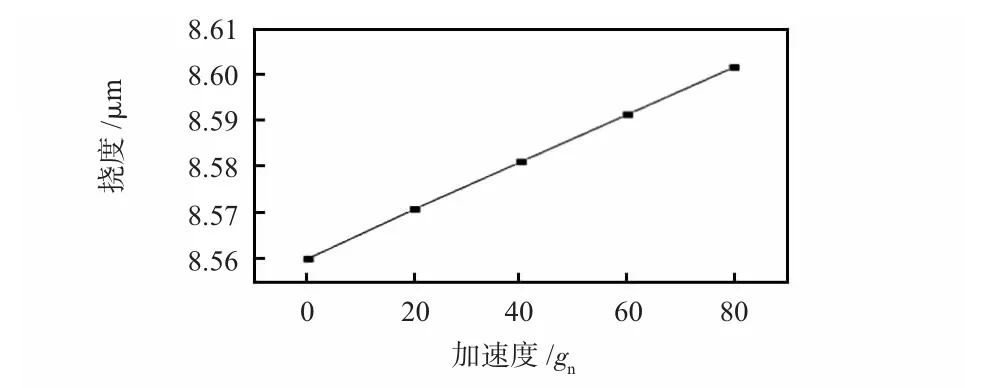
圖3 沿Z 軸負方向的加速度對彎曲懸臂梁撓度的影響Fig 3 Influence of acceleration along Z-axis direction on deflection of curved cantilever

從圖3 中可以看出:Z 軸負方向的加速度越大，彎曲懸臂梁相對于初始撓度的位移越大，當加速度大小達到80 gn時，彎曲懸臂梁上各點相對于初始撓度的位移變化達到最大，懸臂梁上各點的位移如圖4 所示。

由圖4 可以看出:當存在80 gn，沿Z 軸負方向的加速度時，彎曲懸臂梁沿Z 軸負方向產生相對位移，位移最大變化量為0.036 7 μm。

2.1.2 Z 軸正方向的加速度對撓度影響

圖4 沿Z 軸負方向的加速度為80 gn 時彎曲懸臂梁上各點的相對位移變化Fig 4 Relative displacement change of each point on curved antilever while acceleration is 80 gn along Z-axis negative direction

有限元模擬條件:使用2.1.1 中的簡易模型，單位依舊為mm。加速度分別取20，40，60，80 gn，沿Z 軸正方向，從后處理中得出相對位移的變化，再加上初始撓度，求得彎曲懸臂的實際撓度，繪制成曲線圖，如圖5 所示。

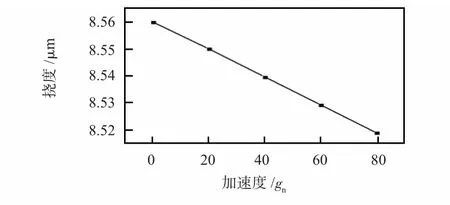
圖5 沿Z 軸正方向的加速度對彎曲懸臂梁撓度的影響Fig 5 Influence of acceleration along Z-axis direction on deflection of curved cantilever

從圖5 中可以看出:Z 軸正方向的加速度越大，彎曲懸臂梁的撓度變化越小，當加速度大小達到80 gn時，彎曲懸臂梁上各點相對于初始撓度的位移變化達到最大，懸臂梁上各點的位移如圖6 所示。

圖6 沿Z 軸正方向的加速度為80 gn 時彎曲懸臂梁上各點相對于初始位移的變化Fig 6 Change of each points on curved cantilever relative to initial displacements while acceleration is 80 gn along Z-axis direction

由圖6 可以看出:當存在為80 gn，沿Z 軸正方向的加速度時，彎曲懸臂梁沿Z 軸正方向產生相對位移，相對于位移變化量為0.041 0 μm。

2.2 溫度場對復合薄膜彎曲懸臂梁撓度影響

有限元模擬條件:由于模型中的空氣、腔體和加熱器都要參加計算，使用完整的模型，模型的尺寸單位設定為m。(下文的模擬中，都使用這個模型)在實際情況中，由于器件的供電電池所提供的電壓是一定的，所以，加熱器所達到的相對穩定的溫度也是一定的，對加熱器加載溫度時，只加載360 K 的溫度，腔體中會產生一個變化的梯度溫度場，溫度最終會達到穩定，在腔內溫度到達穩定的過程中，彎曲懸臂梁會在Z 軸方向上受熱產生形變［7］，如圖7 所示。

圖7 加熱器加載溫度360K 時彎曲懸臂梁上各點相對于初始位移的變化Fig 7 Change of each points on curved cantilever relative to initial displacements while load temperature of heater is 360K

由圖7 可以看出:當加熱器溫度加載360 K 時，彎曲懸臂梁相對位移的最大變化量為2.721 μm。

2.3 耦合場對復合薄膜彎曲懸臂梁撓度影響

2.3.1 加速度沿Z 軸正方向且加熱器恒溫保持360 K

有限元模擬條件:加速度分析步中加載加速度分別為20，40，60，80 gn，沿Z 軸負方向。溫度分析步中，對加熱器加載360 K 的溫度，彎曲懸臂梁在耦合場的作用下發生形變［8］，從后處理中得出相對位移的變化，再考慮初始撓度的大小，從而求得彎曲懸臂梁的實際撓度，如圖8 所示。

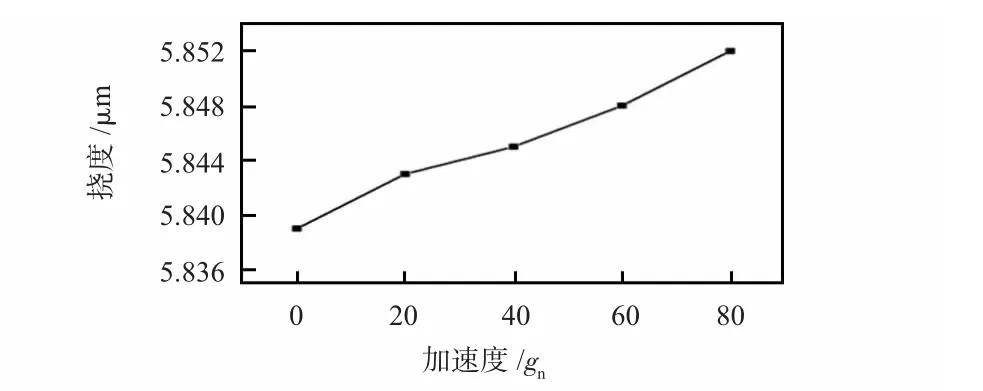
圖8 360 K 時沿Z 軸負方向的加速度對彎曲懸臂梁撓度的影響Fig 8 Influence of acceleration along Z-axis negative direction on deflection of curved cantilever，at the temperature of 360 K

從圖8 中可以看出:沿Z 軸負方向的加速度越大，彎曲懸臂梁的撓度越大，當加速度大小達到80 gn時，彎曲懸臂梁上各點相對于初始撓度的位移變化達到最大，懸臂梁上各點的位移如圖9 所示。

由圖9 可以看出:加速度為－80 gn，加熱器加載溫度為360 K 時，彎曲懸臂梁相對位移的最大變化量為2.717 μm。

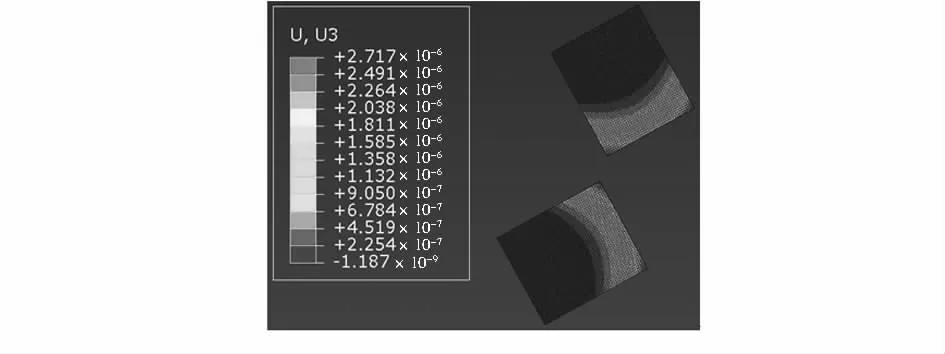
圖9 加速度為-120 gn 與加載溫度為360 K 時的彎曲懸臂梁上各點相對于初始位移的變化大小Fig 9 Change of relative to initial displacements of each points on curved cantilever while acceleration is-120 gn，load temperature is 360 K

2.3.2 加速度沿Z 軸正方向且加熱器恒溫保持360 K

有限元模擬條件:加速度分析步中加載加速度，大小分別取20，40，60，80 gn，方向沿Z 軸正方向。溫度分析步中，對加熱器加載360 K 的溫度，彎曲懸臂梁在耦合場的作用下發生形變，從后處理中得出相對位移的變化，再考慮初始撓度的大小，從而求得彎曲懸臂梁的實際撓度，如圖10 所示。

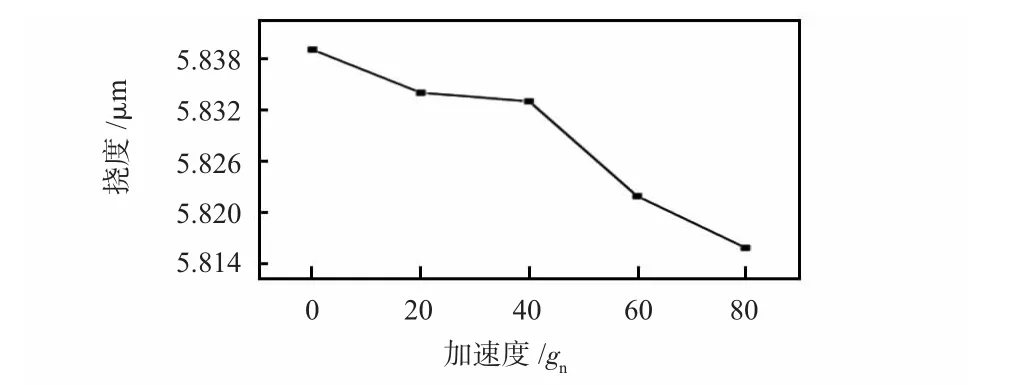
圖10 360 K 時沿Z 軸正方向的加速度對彎曲懸臂梁撓度的影響Fig 10 Influence of acceleration along Z-axis positive direction on deflection of curved cantilever，at the temperature of 360 K

從圖10 中可以看出:Z 軸正方向的加速度越大，彎曲懸臂梁的撓度越小，當加速度大小達到80 gn時，彎曲懸臂梁上各點相對于初始撓度的位移變化達到最大，懸臂梁上各點的位移如圖11 所示。

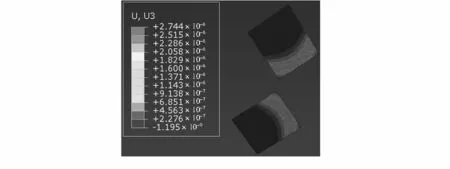
圖11 加速度為80 gn 且加載溫度為360 K 時的彎曲懸臂梁上各點相對于初始位移的變化大小Fig 11 Changes of each points on curved cantilever relaive to initial displacements while acceleration is 80 gn and load temperature is 360 K

由圖11 可以看出:加速度為80 gn，加熱器加載溫度為360 K 時，彎曲懸臂梁相對位移的最大變化量為2.744 μm。

3 結 論

通過ABAQUS 軟件對半導體硅基復合薄膜彎曲懸臂梁在多物理場中的撓度變化進行有限元分析，并對影響撓度變化的因素進行分析比較，可以為器件在實際生產過程中提供一些理論指導和幫助。仿真結果表明:當線性增加沿Z 軸負方向的加速度時，彎曲懸臂梁上的撓度也隨之線性增加，最大值為8.596 7 μm;當線性增加沿Z 軸正方向的加速度時，彎曲懸臂梁上的撓度隨之線性減小，最小值為8.519 0 μm;當加熱器的加載溫度為360K，沒有加速度作用時，彎曲懸臂梁的撓度變化為5.848 μm;當加熱器的加載溫度為360 K，沿Z 軸負方向的加速度線性增加時，彎曲懸臂梁的撓度變化也大致呈線性增加，當加速度達到80 gn時，彎曲懸臂梁的撓度為5.843 μm，當加熱器的加載溫度為360 K，沿Z 軸正方向的加速度線性增加時，彎曲懸臂梁的撓度變化也大致呈線性減少，當加速度達到80 gn時，彎曲懸臂梁的撓度為5.816 μm。通過以上分析，器件Z 軸腔在檢測加速度時，彎曲懸臂梁的撓度和加速度之間存在著一定的函數關系，這對于器件的信號檢測是十分有利的。

［1］ 李 鵬，李昕欣，王躍林.壓阻式二氧化硅微懸臂梁化學氣體傳感器［J］.傳感器學報，2007(10):1004－1699.

［2］ 石亦平，周玉蓉.ABAQUS 實例詳解［M］.北京:機械工業出版社，2006.

［3］ Leman O，Mailly F，Latorre L，et al.Noise analysis of a first-order thermal sigma delta architecture for convective accelerometers［J］.Analog Integr Circuits S，2010，63(3):415－423.

［4］ Choi J C，Kong S H.Performance analysis of a convection-based tilt sensor［J］.Jap J Appli Phys，2010，49(6):06GN15.

［5］ 李純金，杜佐飛.大彎曲半徑管材推彎回彈有限元分析［J］.機械設計與制造，2013(6):94－97.

［6］ 俞 誠.等離子氮化硅應力的研究［J］.半導體技術，1996(3):26－28.

［7］ 劉雙麗.雙金屬熱制動器的設計與仿真［J］.中北大學學報，2008(29):554－557.

［8］ 鄭文濤，徐永超，張士宏.鋁合金手機殼的溫熱液壓成型實驗及模擬研究［J］.塑性工程學報，2006(5):92－95.