基于和聲搜索的低延遲和低能耗無線傳感器網絡*

彭珍瑞，李 輝，董海棠，殷 紅

(蘭州交通大學 機電工程學院，甘肅 蘭州730070)

0 引 言

無線傳感器網絡(WSNs)節點結構緊湊，重量輕，采用電池供電，一般情況下，節點分布在不便于維護的惡劣環境中，必須通過各種手段節約傳感器節點能量。另外，盡量減小延遲保證信息獲取的實時性是無線傳感器網絡的更高性能的要求［1，2］。目前大多數節能算法通過分層傳輸數據包方法實現，如LEACH 算法［3］、PEGASIS 算法［4］等。相對于節點到基站間的數據直接傳輸，分層方法減小了傳輸距離，降低了能耗，但算法中簇內成員在將數據送到簇頭節點時存在排隊競爭，同時多跳發送數據到基站，增大了網絡的延遲，影響網絡實時性。和聲搜索(harmony search，HS)算法［5］作為一種新的啟發式算法，在解決車輛運輸問題［6］、水網設計［7］等方面都取得了一系列的研究成果。

本文提出一種基于和聲搜索算法的無線傳感器網絡最優路徑選取方法，旨在保證傳輸能耗較小的前提下，降低網絡的傳輸延遲，完成對能量和傳輸延遲兩方面的優化。

1 無線傳感器網絡模型建立

1.1 路徑傳輸延遲［2］

路徑傳輸延遲是指數據包從該路徑的源節點發送到該路徑的目的節點所需要的時間，整個網絡信息交互導致的通信延遲由四部分組成:處理延遲、排隊延遲、傳輸延遲和傳播延遲。處理延遲由傳感器節點的處理器決定，傳輸延遲和傳播延遲分別由網絡帶寬和信號傳播速度決定，這三種網絡延遲條件恒定，所以，選取相同的權值因子，將這三種延遲視為只與傳輸路徑的跳數有關，通過中間節點的數量越多，則延遲越高，即通過單個節點的網絡延遲為χ。而減小排隊延遲則需要限制數據流盡量少地通過某同一節點進行中轉，減少數據傳輸之間的競爭。若節點等待接收一個數據包的網絡延遲為w，若該節點有k 個數據包等待接收，則網絡延遲為k·w。假設網絡有一條傳輸路徑從V0將數據發送到Vn，路徑P 為(V0，V1，…，Vi，…，Vn)，di為節點i 與上一個節點i－1 之間的傳輸延遲，di=χ+kiw，則該路徑P 的網絡延遲Dp為

假設從節點V0將數據發送到Vn有m 條路徑，則每條路徑被選中的概率為

1.2 網絡能耗模型［1］

無線傳感器網絡節點的能耗通常由三部分組成:微控制器單元(MCU)、收發單元(TCR)、傳感器主板(SB)。每個部分都會有一定的能量消耗，所以，傳感器節點i 能耗可以表示為

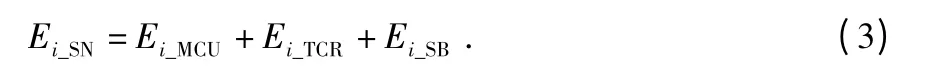
其中，Ei_MCU為傳感器微控制單元消耗能量;Ei_TCR為傳感器收發單元消耗的能量;Ei_SB為傳感器主板消耗的能量。收發單元消耗的能量又可以分為接收數據的能耗Ei_TCR_RX和發送數據產生的能耗Ei_TCR_TX(di)，所以，選擇路徑P 能量消耗為

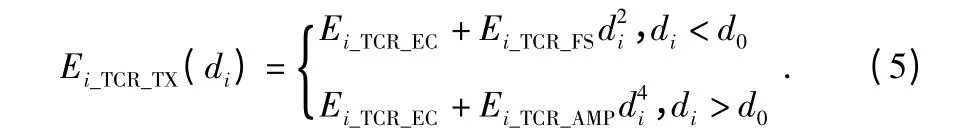
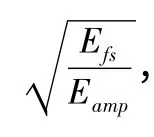
2 和聲搜索算法概述

和聲搜索算法將樂器聲調的和聲類比于優化問題中的解向量，對音樂的評價對應優化問題的目標函數值［5］。和聲搜索的計算步驟如下:

初始化問題和算法參數

1)優化問題描述如下

其中，f(x)為目標函數，x 為由決策變量xi構成的解向量，i=1，2，…，N，每一個決策的值域為Xi。和聲記憶庫的大小定義為HMS、和聲記憶庫取值概率HMCR、音調微調概率PAR、音調微調帶寬bw、創作的次數Tmax。

2)初始化和聲記憶庫

隨機生成HMS 個和聲x1，x2，…，xHMS放入和聲記憶庫，和聲記憶庫形式如下

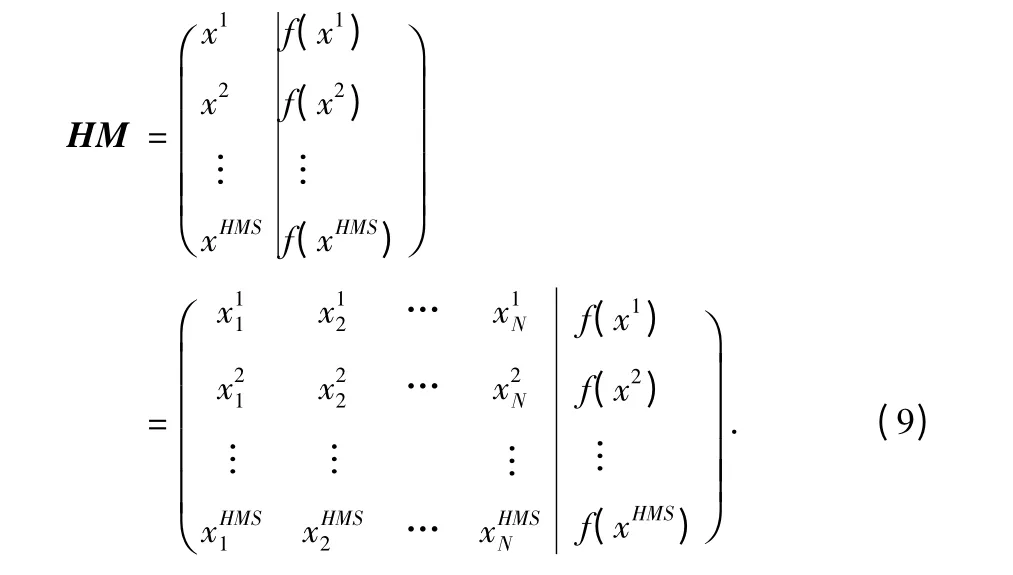
3)生成一個新的和聲

生成新的和聲x'i=［x'1，x'2，…，x'N］，新的和聲每一個音調x'i(i=1，2，…，N)通過以下三種機理產生:a.學習和聲記憶庫;b.音調微調;c.隨機選擇音調。

4)更新和聲記憶庫

對第三步中的新解進行評估，如果優于HM 中的函數值最差的一個，則將新解更新至HM 中。

5)檢查是否達到算法終止條件

重復步驟第3 步和第4 步，直到創作(迭代)次數達到Tmax為止。

3 基于和聲搜索算法的無線傳感器網絡模型求解

3.1 路徑生成的編碼方式

和聲搜索算法應用于無線傳感器網絡數據傳輸中，最棘手的問題在于如何將網絡中的路徑編碼到和聲記憶庫中，同時，編碼方式會對搜索最優路徑的有效性有重要影響。本文采用基于優先級路徑編碼方式［8］。

假設網絡中的節點數目為Nmax，同時將網絡中的節點編號為將被選入傳輸路徑中的節點的集合，xk表示和聲記憶庫中的變量，該變量賦值為－2/Nmax～2/Nmax的隨機數。路徑從節點1 開始，逐個產生，當每次有新的節點加入時，該節點對應在的變量將被賦值較大的負優先值－2/Nmax，使得該節點很難被再次選中。具體算法步驟:

2)判斷是否滿足終止條件，如果tk=Nmax或跳轉到第4 步;否則k=k+1，跳轉到第3 步。

3)路徑拓展，選擇與節點tk－1有數據鏈接，同時節點優先值最大的節點作為下一跳的節點xk(tk)=－2/Nmax，跳轉到第2 步。

4)路徑完成，如果最后得到的終止節點為目標節點，則生成的集合為有效路徑;若終止節點不為目標節點，則為無效路徑。

在Matlab 仿真環境下，以N=20 為例，在100 m×100 m的區域內隨機生成20 個節點，假定每個節點的傳輸半徑為R，在此例中R 取50 m，即兩節點間的距離小于50 m，視為相鄰節點，數據包需要從節點1 發送到節點20，網絡拓撲結構如圖1 所示。同時隨機生成編碼如表1。

圖1 網絡拓撲結構圖Fig 1 Structure diagram of network topology

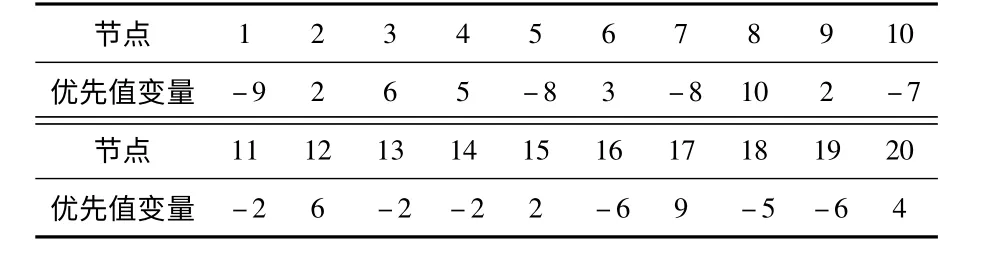
表1 編碼表Tab 1 Encoding table

由拓撲結構可知，節點1 與節點2，3，5，6，7 可以產生數據通信，比較節點2，3，5，6，7 對應的變量優先值，選擇節點3 作為下一跳的節點，并將節點1 的變量賦值為－10，確保其在后面的搜索中不會被選為中轉點，同時節點3 和2，4，5，9，10 有數據鏈接，比較后確定節點4 作為下一跳的中轉節點，依此類推，得到傳輸路徑V={1，3，4，8，17，20}。

3.2 基于和聲搜索的算法流程

由對網絡模型的分析可知，網絡建立由網絡延遲和通信能耗兩方面因素決定，通過用戶對網絡中延遲和能耗的要求不同，延遲和能耗權重不同，分別設為α 和β，α+β=1。和聲向量的質量通過目標函數值來判斷，對低延遲和低功耗的目標定義目標函數為

考慮延遲和能耗影響，得到算法流程如圖2 所示。

3.3 結果與分析

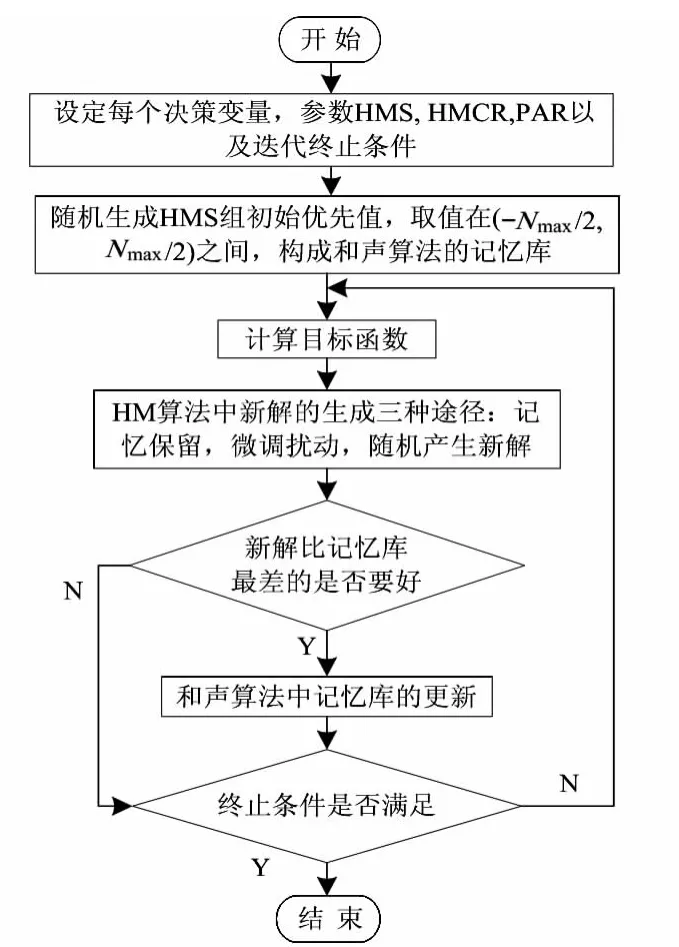
圖2 算法流程圖Fig 2 Flow chart of algorithm

在Matlab 環境下，對100 個節點的網絡應用和聲搜索算法進行仿真實驗，考慮傳感器相鄰節點距離R ＜30 m。對延遲和能量消耗兩個目標所占權重值的不同，分析延遲和能耗對網絡數據傳輸路徑選擇的影響。

分別取α=0，β=1;α=0.5，β=0.5;α=1，β=0;迭代次數J=1200;圖3(a)為網絡能耗圖，圖3(b)為網絡延遲圖。

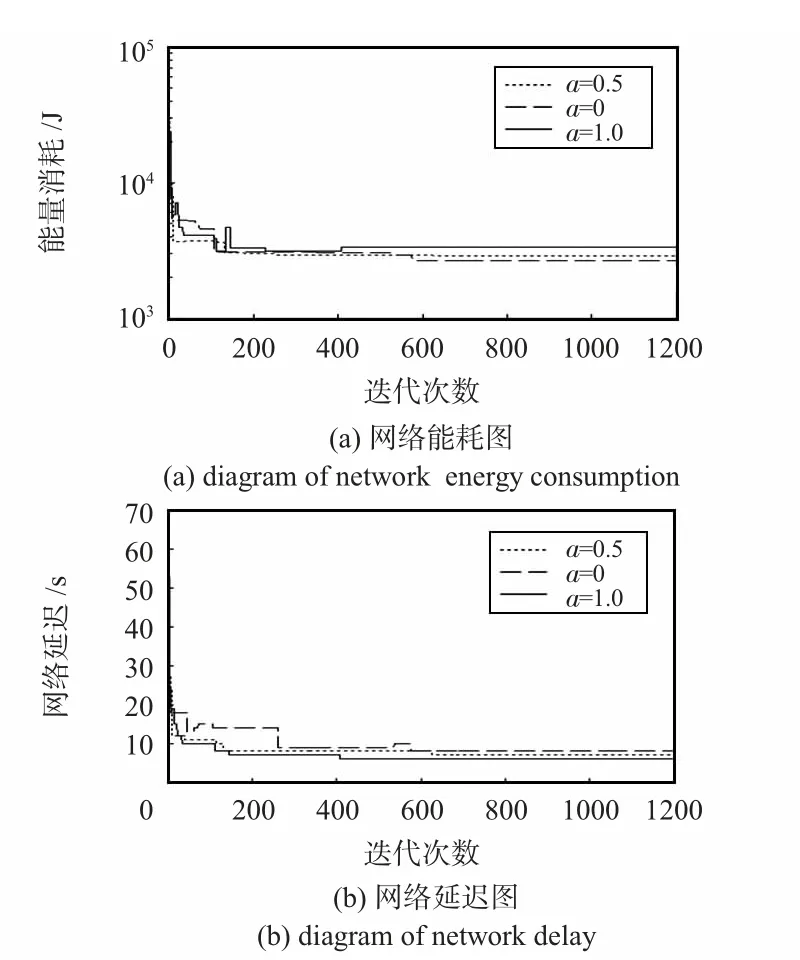
圖3 網絡能耗和網絡延遲圖Fig 3 Diagram of network energy consumption and network delay

由圖3 變化趨勢可以看出:在運行約600 代后，基本可以得到穩定的數據傳輸路徑。由記錄的數據可知，取α=0，β=1，即單獨考慮能耗影響因素，路徑產生的能耗為2 695.86 J，延遲為10.4 s;取α=1，β=0，即單獨考慮降低延遲，導致的延遲為6.2 s，能耗為3 355.73 J;取α=0.5，β=0.5，即給定選擇路徑中能耗及延遲各占50%權重，則產生的路徑能耗為2 851.1 J，延遲為7.4 s。比較3 組數據，當優先考慮能耗因素，延遲會相應偏高，而優先考慮延遲因素，則能耗相對較高，雖然都未達到單方面的最優值，但綜合考慮能量消耗和網絡延遲兩方面因素，可以得到滿足總目標的較優傳輸路徑。由此可見，網絡延遲和網絡中的能量消耗兩方面因素相互制約，無法同時達到最優狀態，而給延遲和能耗設定相應的權重值，可以得到用戶所需求的相應優化路徑。

4 結 論

本文應用和聲搜索算法解決無線傳感器網絡中低延遲和低能耗的雙目標優化問題。分析了網絡中延遲和能耗模型，同時在找尋最優路徑時，采用基于優先級的路徑編碼算法，迭代更新和聲記憶庫。在Matlab 仿真環境下對網絡進行仿真實驗后，驗證網絡延遲和網絡中的能量消耗的相互制約關系，可以根據用戶對網絡的需求，得到相應的優化路徑。

［1］ Cheng Chi－Tsun，Tse Chi K，Lau Francis C.M.A delay－aware data collection network structure for wireless sensor networks［J］.IEEE Sensors Journal，2011，11(3):699－710.

［2］ 顧洪軍，張 佐，吳秋峰.網絡控制系統中周期性通信的實時性充分條件［J］.測控技術，2001，20(6):1－4.

［3］ Heinzelman W，Chandrakasan A，Balakrishnan H.An applicationspecific protocol architecture for wireless micro sensor networks［J］.IEEE Translations on Wireless Communications，2002，1(4):660－670.

［4］ Lindsey S，Raghavendra C S.PEGASIS:Power－efficient gathering in sensor information systems［C］∥Proc IEEE Conf Aerosp Big Sky，MT，USA，2002:1125－1130.

［5］ Geem Z，Kim J，Loganathan G.A new heuristic optimization algorithm:Harmony search［J］.Simulation，2001，76(2):60－68.

［6］ Geem Z W，Lee K S，Park Y.Application of harmony search to vehicle routing［J］.American Journal of Applied Sciences，2005，2(12):1552－1557.

［7］ Geem Z W.Optimal cost design of water distribution networks using harmony search［J］.Engineering Optimization，2006，38(3):259－280.

［8］ Mohemmed A W，Sahoo N C，Geok T K.Solving shortest path problem using particle swarm optimization［J］.Applied Soft Computing，2008，8(4):1643－1653.