典型場景下電波傳播特性建模

郭淑霞，單雄軍，張 政，高 穎

(1.西北工業大學無人機特種技術重點實驗室，西安710065;2.西北工業大學航海學院，西安710072)

對 Q

引 言

無論是雷達、衛星導航系統，還是電子對抗，都依賴于無線電波傳輸，避免不了對電波傳播特性的分析。不能使用微擾、基爾霍夫法等傳統方法來求解掠入射時粗糙的表面散射性能。近期有一些使用改進的算法來解掠入射問題的方法，能夠定量分析掠入射多重散射特性，從而很好地求解大入射角散射系數問題［1］，但較難把大氣波導影響加入其中;且需要利用積分數值法進行計算，計算量相當大［2］。利用拋物方程計算求解復雜大氣條件，可應用于電波環境中。其中，阻抗邊界條件可用混合傅里葉變換(mixed Fourier transform，MFT)處理，進而用離散混合傅里葉變換(discrete mixed Fourier transform，DMFT)實現。

中國電波研究所已對森林中的電磁波傳播情況進行了實測和分析，并提出了經驗模型。但是經驗模型并不能準確預測地形與多徑的傳播特性影響［3］。LI等人對森林中的4層模型進行了研究［4］。然而，很難運用解析方法來分析森林與大氣波導等電磁環境特性。

在森林電波環境分析中，對森林的電磁波的傳播問題采用拋物方程進行求解，并且利用計算的結果和Tamir模型結果相互比較，證明拋物方程法在森林電波環境中可行性［5］。

采用拋物方程法對正常的大氣分布、動態分析地海面情況下電波傳播損耗的分析和計算，表明電波傳播特性對特定環境中雷達和通信系統的正常工作產生重要的影響;但它未考慮粗糙表面及大氣不均勻等因素的影響［6-8］。

基于拋物方程法分析粗糙海面上的電波傳播特性，對于海面電波環境分析有較好的借鑒作用［9］。

以上僅考慮采用拋物方程法求解某一特定場景下電波傳播損耗的問題。針對典型場景(如海上、山區、丘陵、城區)問題，無法使用已有典型場景下的基礎模型來全面表達電波傳播特性［10］。本文中建立一種適用于不同傳輸場景、基于確定性拋物方程的統一電波傳播模型，可求解典型場景下的電波傳播衰落問題。

1 典型場景分析

目前武器裝備面臨的場景主要有海上、山區、丘陵、城區，因此，這4個場景是本文中需要研究的典型場景。通過介電常數和電導率來劃分武器裝備所在的不同場景。當武器裝備依次從海上、山區、丘陵、城區區域經過時，介電常數和電導率會發生變化，即拋物方程的邊界條件發生變化，拋物方程的解相應發生改變。

針對本文中的典型場景，畫出典型場景(海上、山區、丘陵、城區)的示意圖，橫坐標為區域，縱坐標為高度。如圖1所示。

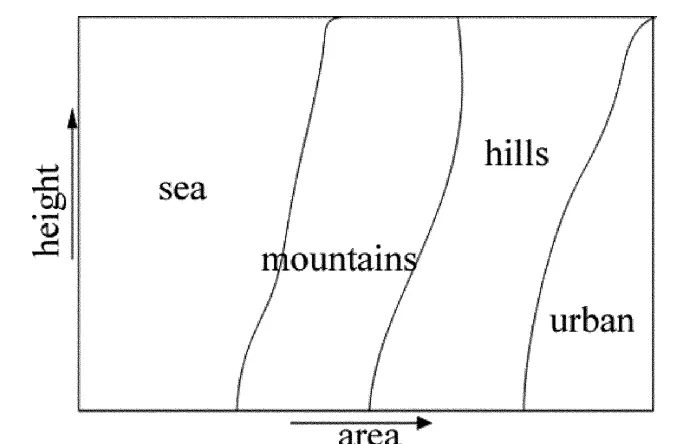
Fig.1 Schematic diagram of typical scenarios

以無人機為例。處于無人機的角度上，橫坐標的區域表示無人機所在的區域，縱坐標的高度表示無人機遠離研究對象的高度。假設無人機從海上、山區、丘陵、城區區域依次飛過時，通過介電常數和電導率的變化，即可得知無人機所在的區域。表1是典型場景下的介電常數和電導率的分布表。

Table 1 Dielectric constant and conductivity distribution under typical scenarios

已知典型場景下的介電常數和電導率，即可確定邊界條件，運用統一電波傳播模型可求得特定的解。得出仿真結果與相應的模型進行比較，驗證統一電波傳播模型的正確性。

2 基于拋物方程建立統一電波傳播模型

電磁場諧因子是 e-iωt，其中，ω 為角頻率，t為時間。所有電磁場分量和方位角都沒有關系，方位角相互對稱。方程在直角坐標系中可表示為:

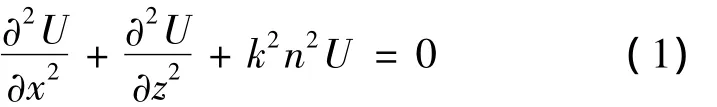
式中，z為高度，x為距離，U為波函數，k為真空中的傳播常數，n為折射指數。

根據微分算子理論對(1)式進行因式分解，可得:

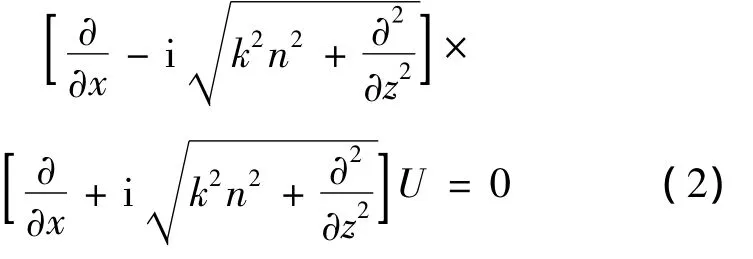
式中，電波的前向傳播對應前一個微分算子;電波的后向傳播對應后一個微分算子，選取拋物方程的前向傳播為研究對象，忽略后向傳播的影響。得到近似拋物方程為:

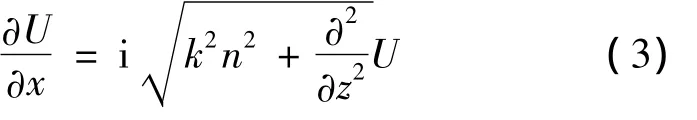
對 Q

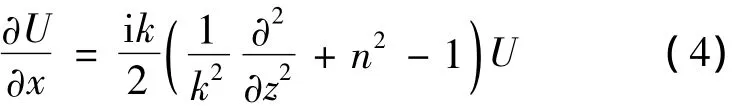
用Fourier分步步進法求解窄角拋物方程(電波傳播仰角小于15°)時，在x+Δx的場可似為:

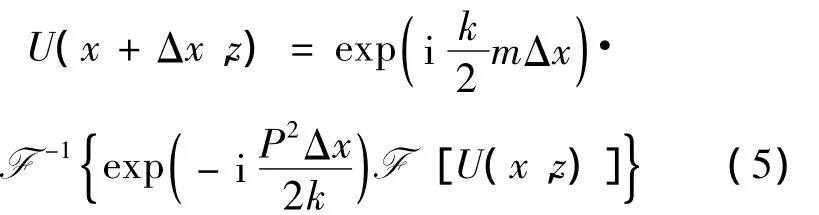
式中，m=n2-1+2z/ae，包含了地球曲率的影響，設地球的半徑是ae為Fourier變換是相應的Fourier逆變換;P為Fourier變換的頻域變量，通常P=ksinθ，θ為電波傳播方向到水平方向的角度［11-12］。可以用合適的Fourier變換來表示其中的阻抗邊界條件。

模型精度受電波傳播仰角的影響比較大，當電波傳播仰角大于15°時，應用窄角拋物方程建立的計算模型會產生較大誤差。所以該模型合適的仰角小于15°。在推導方程解時，將場量進行分解，分解后結果為兩個不同因子的乘積。根據以上理論，傳播損耗L在數值上等于傳播空間的傳播損耗LBF與發射天線的空間發散損耗LPF之和。

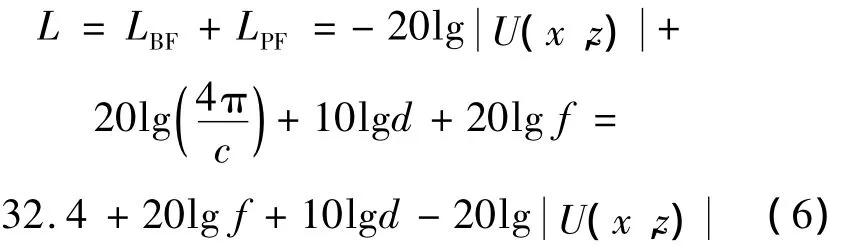
式中，c為光速，d為傳播距離，f為頻率。

用分布步進法來求拋物方程(parabolic equations，PE)時，在相應的譜域中通過Fourier變換加入邊界條件。對完純導電平面，磁場或電場分別滿足Neumann或Dirichlet的邊界條件。通過鏡像理論分析，邊界條件的滿足需邊界有偶對稱或奇對稱。因此，Fourier變換可以變為單邊余弦變換或正弦變換。

對導電的平面而言，電磁場的分量應滿足Leontovich邊界條件:

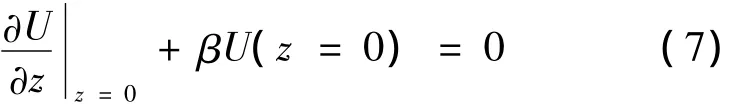
式中，

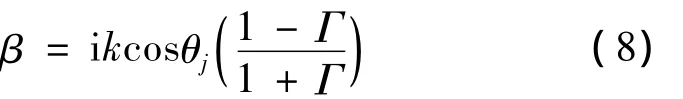
式中，Γ是邊界Fresnel反射系數，θj是電波入射角。采用Fourier變換法求解滿足阻抗邊界條件(7)式的拋物方程時，通過引入混合Fourier變換就可滿足邊界條件，進而可以采用DMFT進行快速的求解。

基于PE建立統一電波傳播模型，求解典型場景下電波傳播衰落問題，即求解不同傳輸場景下拋物方程的邊界條件問題。

分析典型的場景對電磁波傳播的影響，可把典型的場景對應等效為損耗介質層［4，13］，并且用等效的反射系數ξ來表示:

式中，ε和σ分別是把典型的場景等效為損耗介質層的介電常數與電導率，λ為波長。

圖2表明，在4種不同的水平傳播距離(分別為10km，50km，100km和150km)情況下，電磁信號隨高度變化的傳播損耗。

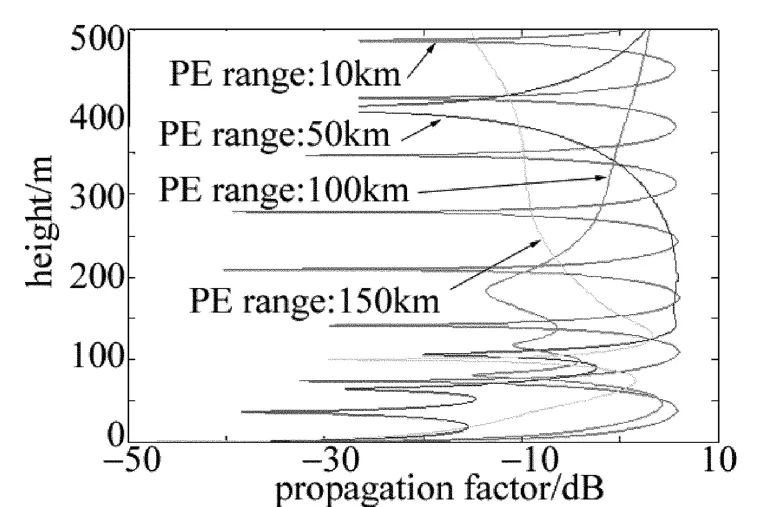
Fig.2 Attenuation characteristics of electromagnetic signal based PE equation

圖3 表明采用水平極化方式，在不同距離及不同高度情況下，電磁信號傳播隨水平距離及高度變化的傳播損耗。圖中，蒸發波導高度為35m。不同的損耗值對應相應的顏色，可知傳播損耗值隨著距離增加而增大。

Fig.3 Signal propagation loss under horizontal polarization with different distance and different height

3 仿真分析

為了進一步驗證統一電波傳播模型的正確性，下面用統一電波傳播模型計算典型場景下電波傳播特性，并與相應的模型進行比較。

3．1 海上場景分析

假設海面上大氣折射率為1、天線類型是高斯天線、發射天線水平極化、高30m、頻率900MHz;海水介電常數為70、電導率為5S/m;最大傳播距離為200km。用統一電波傳播模型計算風速為10m/s的海面電波傳播特性，距離為5km，海浪為中浪，浪高2.5m，海面的高度均方根差為0.63m，電波傳播仰角小于15°。

圖4顯示傳播因子隨高度的變化，同時給出了Miller-Brown模型的結果。結果顯示，兩種方法結果較吻合，峰值與零點位置也一致。

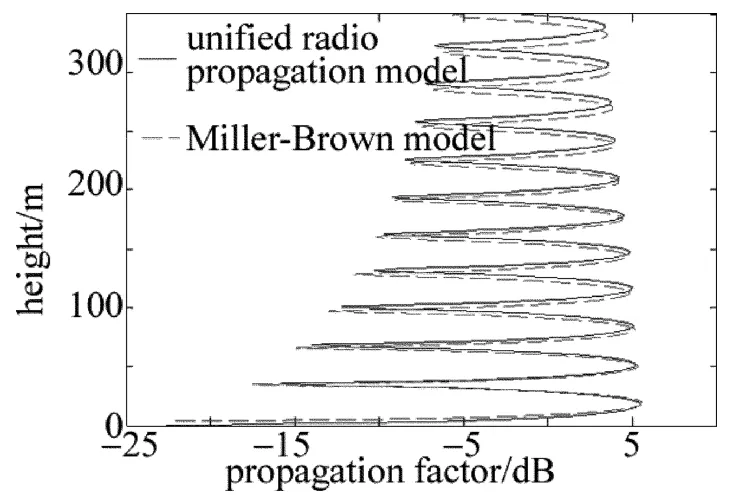
Fig.4 Comparison between uniform radio propagation model and Miller-Brown model

此算例采用統一電波傳播模型及阻抗邊界條件的方法，仿真顯示了統一電波傳播模型能求解該問題。為驗證統一電波傳播模型的正確性，本文中計算了海面上的電波傳播因子，并且和Miller-Brown模型相互的比較，二者能夠很好地吻合。統一電波傳播模型也可以分析海面的復雜電磁波環境和地形，而且也能分析復雜海洋環境的傳播特性。

3．2 城區場景分析

以雙射線模型作為基準參考模型，驗證了統一電波傳播模型的正確性。雙射線模型的傳播因子理論值為:

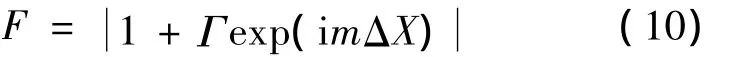
式中，ΔX為直射波與反射波的路程差，m為自由空間波數。

計算了一個簡單小區內電波傳播情況，其中，頻率為900MHz，垂直極化的發射天線高度為5m，在小區內位于(41.8m，7.41m)處，長方體建筑尺寸為17m(長)×17m(寬)×24m(高)，街道的寬度為12m，接收點距發射天線的距離為850m，建筑表面的介電常數為4，電導率為0.05μS/m，電波傳播仰角小于15°。采用統一電波傳播模型的計算結果與射線追蹤模型結果比較，如圖5所示。

為了驗證統一電波傳播模型的正確性，此算例計算了城區建筑物上的電波傳播因子，并與射線追蹤法進行比較，二者吻合較好，驗證了模型的正確性。這樣的結果符合電波傳播的物理機制。

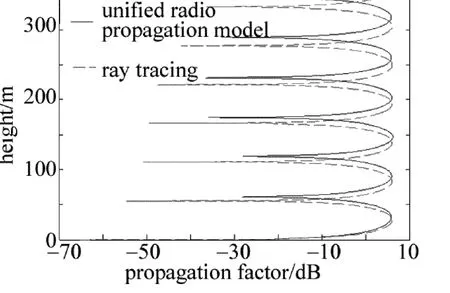
Fig.5 Comparison between uniform radio propagation model and ray tracing model

4 結束語

不同的電波傳播場景需建立相應的傳播模型，針對不同型場景問題，無法使用已有典型場景下的基礎模型來全面表達電波傳播特性。作者建立了一種適用于多傳輸場景、基于確定性拋物方程的統一電波傳播模型，求解典型場景下的電波傳播衰落問題，即求解不同邊界條件下拋物方程的解。分析典型場景對電波傳播的影響時，可把典型場景等效為損耗介質層，得到拋物方程的邊界條件，進而可得到電波在典型場景下的傳播損耗。在不同輸場景下，將統一電波傳播模型與Miller-Brown模型、射線追蹤模型進行比較，結果較吻合，驗證了其正確性。

［1］ HUAN Z G，TONG Ch M，HU G P.Study of low-grazing angle scattering effect from gaussian rough surface［J］.Electronics ＆ Information Technology，2007，29(2):482-485(in Chinese).

［2］ GUO J Y，WANG J Y，LONG Y L.Analysis of radio propagation over rough sea surface with parabolic equation［J］.Journal on Communications，2009，30(6):47-52(in Chinese).

［3］ GUO J Y，WANG J Y，LONG Y L.Analysis of radio propagation in partly forested terrain environment using parabolic equation approach［J］.Chinese Journal of Radio Science，2008，23(6):1045-1050(in Chinese).

［4］ LI L W，LEE Ch K，YEO T S，et al.Wave mode and path characteristics in a four-layered anisotropic forest environment［J］.IEEE Transactions on Antennas and Propagation，2004，52(9):2445-2455.

［5］ GUO J Y，WANG J Y，LONG Y L.Parabolic equation model for wave propagation in forest environments［J］.Chinese Journal of Radio Science，2007，22(6):1042-1046(in Chinese).

［6］ FENG K Sh，GE D B，LUO X Y，et al.Study on effects of the complex environment on radar and communication propagation with the method of parabolic equation［J］.Chinese Journal of Electronics，2000，28(6):68-71(in Chinese).

［7］ LI D X，YAN R J，GUAN W，et al.Research on two-way parabolic equation modeling under irregular terrain environment［J］.Journal of Astronautics，2012，33(2):235-241(in Chinese).

［8］ CHEN H F，CHEN Y，LI Y Y，et al.Simulation of atmospheric transmission characteristics of laser at 1.06μm［J］.Laser Technology，2014，38(2):266-269(in Chinese).

［9］ WANG Z L，FAN W Sh，ZHENG L H.Study and simulation on sea-surface propagation prediction model［J］.Chinese Journal of Radio Science，2008，23(6):1095-1099(in Chinese).

［10］ WANG K，YAN Y Q，LONG Y L，et al.Two-way parabolic equation approach for modeling radio wave propagation in the presence of multiple knife edges［J］.Chinese Journal of Radio Science，2011，26(6):1058-1064(in Chinese).

［11］ CAO S P，WANG W F，XUE X Ch.Dynamic 3-D shape measurement based on de-interlaced images by Fourier transform［J］.Laser Technology，2013，37(6):736-741(in Chinese).

［12］ MO X F，SHI J L，CHEN X G，et al.Measurement of SBS linewidth based on time-domain Fourier transform［J］.Laser Technology，2013，37(5):561-564(in Chinese).

［13］ HOLM P，LUNDBORG B，WAERN A.Parabolic equation technique in vegetation and urban environments［J］.IEEE Transactions on Antennas and Propagation，2003，32(3):464-468.