數學文化研究與傳播
——“第四屆全國數學文化論壇學術會議”綜述

李春蘭

（內蒙古師范大學 數學科學學院，內蒙古 呼和浩特 010022）

數學文化研究與傳播
——“第四屆全國數學文化論壇學術會議”綜述

李春蘭

（內蒙古師范大學 數學科學學院，內蒙古 呼和浩特 010022）

“第四屆全國數學文化論壇學術會議”有3位院士和15位學者分別進行了報告，其中45分鐘和25分鐘的報告各9個．這些報告內容豐富、思想深刻，從不同角度反映了近年來中國數學文化研究和傳播的情況．這次會議主要是圍繞數學文化的種類和特征、數學的應用、中國傳統數學和中國文化、數學史、數學與游戲、數學之美、數學哲學、數學文化的傳播、數學教育等展開研討．

第四屆全國數學文化論壇學術會議；數學文化；數學的應用；數學史；數學哲學

1 會議概述

自2011年開始，由中國數學會主辦的“全國數學文化論壇會議”每年召開一次．首屆“全國數學文化論壇會議”于2011年10月在河北師范大學召開，“第二屆全國數學文化論壇會議”于2012年10月在南京信息工程大學召開，“第三屆全國數學文化論壇學術會議”于2013年8月在沈陽建筑大學召開．

為了更好地交流國內外數學文化研究進展，推進中國數學文化研究，繁榮數學文化，于2014年8月2日至5日，在內蒙古師范大學舉行了“第四屆全國數學文化論壇學術會議”．共有一百六十多位來自全國63個單位的學者出席了會議，其中有3位是中國科學院院士：嚴加安、馬志明和陳永川．在內蒙古師范大學的全力支持下、內蒙古數學學會的協助下、以及中國數學會和國家基金委天元數學基金的資助下，會議取得了圓滿成功．

“第四屆全國數學文化論壇學術會議”組織委員會主席為內蒙古師范大學斯仁道爾吉教授，副主席為內蒙古師范大學劉官廳教授和內蒙古大學楊聯貴教授．學術委員會主席為中國科學院嚴加安院士，副主席為中國科學院、中國數學會秘書長張立群研究員．

會議共有18個報告，45分鐘的特邀報告和25分鐘的報告各9個．這些報告從不同角度很好地反映了近年來中國數學文化研究和傳播的情況．下面列出會議的報告人及其報告的題目．

45分鐘特邀報告：

（1）中國科學院嚴加安院士：概率破玄機，統計解迷離

（2）中國科學院馬志明院士：數學與現代文明

（3）中國科學院陳永川院士：漫談獨立與相關

（4）北京航天航空大學李尚志教授：數學與中國文化

（5）山東大學劉建亞教授：不器之學

（6） 香港浸會大學副校長湯濤教授：通過互聯網推廣數學文化

（7）浙江大學蔡天新教授：十七世紀：天才的世紀

（8）沈陽建筑大學靖新教授：數學模型之美

（9）復旦大學程晉教授：反問題：基于數學模型的研究方法

25分鐘報告：

（1）四川師范大學張紅教授：民國時期數學傳播與四川數學的發展

（2）西北農林科技大學林開亮副教授：華羅庚先生在矩陣論方面的貢獻

（3）西北民族大學范忠雄教授：對弈熵率在藏棋“杰布杰曾”上的應用

（4）河南科技學院郭運瑞教授：我校數學文化課程的教學實踐與在河南高校的影響

（5）內蒙古師范大學代欽教授：釋數學文化

（6）東南大學張福保教授：對數學確定性喪失的再認識

（7）西交利物浦大學劉剛副主任：德國數學展簡介

（8）深圳大學張文俊教授：游戲中的數學思維

（9）內蒙古師范大學郭世榮教授：中國傳統數學詩文歌訣的文化意蘊

2 摭拾內容

“第四屆全國數學文化論壇學術會議”的18個報告，主要是圍繞數學文化的種類和特征、數學的應用、中國傳統數學、數學與中國文化、數學史、數學與游戲、數學之美、數學哲學、數學文化的傳播、數學教育等展開研討．報告內容豐富、思想深刻，為參會代表奉上了豐盛的“數學文化盛宴”．參會代表再一次經歷了數學文化的洗禮，受益匪淺．下面摭拾會議中的報告作簡要的綜述，以便國內學者更好地了解此次會議報告的內容．

2.1 數學文化的界定和種類及其特征

代欽教授在對國內外文化與數學文化之定義進行綜述的基礎上，提出了數學文化的定義，即數學文化是數學知識、思想方法及其在人類活動的應用以及與數學有關的民俗習慣和信仰的總和．他在報告中綜合豐富的案例詳細闡述了數學文化的4種形態：純粹數學形態、學校數學形態、應用數學形態和民族數學形態；以及數學文化的5個特征：規范特征、審美特征、認知特征、歷史特征和價值特征．

2.2 數學的應用

拉普拉斯語“生活中最重要的問題絕大部分只是概率問題”．嚴加安院士長期從事概率論和隨機分析研究，對概率統計的本質有深刻的領悟，曾對概率統計作詩一首——悟道詩：隨機非隨意，概率破玄機．無序隱有序，統計解迷離．在這次報告中，嚴院士以“概率破玄機，統計解迷離”為題，通過日常生活中的一些例子向大家展示概率是如何破玄機和統計是如何解迷離的．其中包括：從“生日問題”談起；條件概率和全概率公式；計算條件概率的貝葉斯公式；如何評估疾病診斷的確診率；如何設計對敏感性問題的社會調查；“辛普森悖論”；“統計平均”的陷阱；“競賽規則”藏玄機；分組混合血標本檢驗既省錢又省時；抽樣調查的結論依賴于樣本量的大小．

一個時代的總的特征在很大程度上與這個時代的數學活動密切相關．馬志明院士通過概述前人的研究成果及其個人的研究發現，以數學與現代生命科學、多媒體中的數學、數學與現代經濟金融等為視角，用豐富生動的實例來說明數學與現代文明是密切相關的．

獨立與相關是數學中的普遍現象，如線性代數中的線性相關與線性無關，概率事件的獨立性與相關性等．陳永川院士分別以線性代數篇、概率統計篇、應用數學篇為主題，以豐富案例為依據，闡述了“獨立與相關”問題．其中“線性代數篇”以Fisher不等式（線性代數的巧妙證明）、Hall婚姻定理（線性代數證明）、Pick定理（來自天書的證明）、Rota基猜想、Wilf猜想、點燈問題等為例；“概率統計篇”以豆科植物莖的顏色（綠色和黃色的比是3∶1）、洗牌問題（只需7次就可將牌洗均勻）、拋硬幣問題（硬幣面朝上和朝下遵循51∶49的比值）、Polya罐子模型、敏感問題調查等為例；“應用數學篇”以網絡溯源、無尺度網絡——這個世界太小了、網絡——跆拳道俱樂部、網絡——用網絡算法對抗犯罪、搜索引擎、訪問網頁記錄數據、Zipf定律、壓縮感知等為例．

學術界將已知原因（輸入）、過程（模型）而探求唯一結果（輸出）的一類問題成為正問題．反問題的研究是目前應用數學研究中的一個熱點研究領域．盡管一些經典反問題的研究可以追溯很早．反問題這一研究領域的興起卻是近幾十年來的事情．在科學研究中經常要通過間接觀測來探求位于不可達、不可觸之處的物質的變化規律；生產中經常要根據特定的功能對產品進行設計，或按照某種目的對流程進行控制．這些都可以提出為某種形式的反問題．程晉教授在報告中指出：“反問題”簡而言之就是由果求因，即由效果、表現反求原因、原像．反問題與正問題是成對出現的．從根本上來講，選擇哪個稱為正問題，哪個稱為反問題嚴格說來都是任意的．反問題研究的核心其實就是反問題的數學研究．反問題的產生是科學研究不斷深化和工程技術迅猛發展的結果，而計算技術的革命又為它提供了重要的物質基礎．反問題的研究已經遍及現代化生產、生活、研究的各個領域．除了有精煉的概括外，程晉教授在報告中還通過一些例子來介紹反問題研究的起源、發展已經將來可能的應用前景．

2.3 中國傳統數學和中國文化

李尚志教授的《數學大觀》一直深受廣大師生的喜愛，可謂是大家百看不厭的“連續劇”．李教授幽默詼諧，在這次報告中，他以一道算術題3×8=23引出“中國文化”．詳細闡述了老和尚判24會有什么后果，以史料、事實等說明這道算術題引發的血案及血案的改良版和海外版．最后，李教授向大家提供了網絡資源，視頻：中國大學視頻公開課李尚志：數學大觀（1—14集）；歐陽夏丹對話李尚志；數學的草根本色：教育人生Mooc∶ www.wemooc.edu.cn→課程；博客：blog.sina.com.cn/kumath．

中國古代數學著作中常以詩詞歌訣表達數學的問題、算法與思想，包含了豐富的文化信息，頗具文化意蘊．郭世榮教授以中國傳統數學著作如《數術記遺》《孫子算經》《張丘建算經》《算學啟蒙》《四元玉鑒》等為例，指出中國傳統數學著作中出現的“歌訣”形式多種多樣，如四言、五言、六言、七言絕句，又如各種詞牌的詞，鳳棲梧、雙搗練、清江引、山破羊、醉太平、雁兒落、皂羅袍、梅氣清、西江月、水仙子、鷓鴣天、駐馬聽，等等，都經常用到，這里將其簡稱為“歌訣”型．郭教授從“歌訣”的歷史概要、表達形式、反映的數學內容、體現的數學文化、簡要的評論等角度闡述中國傳統數學詩文歌訣的文化意蘊．

2.4 數 學 史

17世紀涌現的科學人物并不是最多的，卻都是重量級的：費爾馬、帕斯卡爾、惠更斯、牛頓、斯賓諾莎、萊布尼茲，還有稍早的培根、開普勒、伽利略和笛卡爾，最后3位的學術生涯大部分時光也是在17世紀度過的．不僅如此，其中的多位還橫跨科學與人文兩大領域．蔡天新教授從“意大利文藝復興”談起，主要圍繞“17世紀的科學”和“17世紀的哲學”通過豐富生動的史實來闡明17世紀是天才的世紀．并言簡意賅地說明出現“天才的世紀”的客觀原因．

丘成桐先生曾說，中國近代數學能超越西方或與之并駕齊驅的主要有3個，其中之一就是華羅庚（1910—1985）在多復變函數方面的工作．他在多復變函數方面的貢獻比西方至少早了10年，海外的數學家都很尊重華先生在這方面的成就．在1940年以前，華羅庚的數學研究主要是受到Landau《數論教程》的影響，其成果匯集成專著《堆壘素數論》；在1940年以后，對華羅庚影響越來越深的是Turnbull與Aitken的《矩陣標準型理論導引》，其影響見于華羅庚1940年代關于多復變函數與矩陣幾何的多篇論文．林開亮副教授在報告詳細介紹了華羅庚先生在矩陣論方面所取得的成就以及對海內外學者的影響．

2.5 數學與游戲

張文俊教授通過對一個民間游戲“取石子”及其變形的取勝策略分析，揭示其中蘊含的主要數學思維：逆向思維、極端原理、對稱原理、分類思想、劃歸思想、窮舉方法、歸納猜想、演繹推理，揭示數學與游戲的聯系與區別．

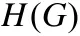
2.6 數學哲學與數學之美

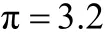
“數學確定性的喪失”的提出對數學界、文化界乃至整個社會的影響是巨大的，相關的研究也很多．張福保教授從數學文化的角度探討了對數學原理的真理性的意義、數學原理的真理性的建立與喪失以及數學體系確定性喪失的一些認識．他強調哥德爾不完全性定理的提出所導致的所謂“數學確定性的喪失”并沒有給數學帶來災難，數學在刻畫現實世界、服務科學技術方面的工具功能進一步凸顯，這一定理只是印證了數學的文化屬性，數學是人類理性精神的產物．在報告中，也簡單介紹了哥德爾不完全性定理在其它領域的文化含義和影響．

數學模型之美，是數學思想、精神之美，是人類創造性活動的展示，是對世界之美的表達．靖新教授以“數學模型之美”為報告主題，其報告內容包括：模型與美、數學模型之美、優美的數學模型賞析、大數據時代數學建模范式的創新．

2.7 數學文化的傳播

日趨流行的互聯網新媒體（尤其是社交媒體）為科學傳播提供了一種更為快捷便利的途徑．結合互聯網技術進行教學，成效可望進一步擴展．湯濤教授提出通過互聯網推廣數學文化，并且重點介紹了他和劉建亞教授主編的刊物《數學文化》，以及《數學文化》引導的善科數學網．在報告中，針對“善科數學網”，湯教授交待的主要內容有：“善科科普”的宗旨、善科文庫、善科書單、微博微信科普、視頻科普等；針對《數學文化》這個刊物，湯教授交待了這個刊物的網址：www.global-sci.org/mc；微博：新浪微博@數學文化，以便大家更方便地去查閱與交流．另外，重點介紹了《數學文化》所包含的欄目：數學人物、數學史林、數學煙云、數學趣談、數學經緯、數學教育、好書推薦．并且分別以“數學教育”和“數學人物”為代表，闡述《數學文化》所刊載的高質量的文章．湯教授的報告，不僅使得參會代表獲得了更多的信息資源，而且加深了參會代表對“數學文化”的認識、拓寬了大家的科研視野．

德國數學展即為IMAGINARY EXHIBITION是一個互動式的巡回展覽．IMAGINARY通過可視化，互動裝置，虛擬世界，3D物體等，以一種有趣，容易理解的方式向參觀者展示了一個基于代數幾何，奇點理論和微分幾何的奇妙的數學世界及相關的理論背景．展覽的主辦方是奧博沃爾法赫數學所．劉剛副主任在報告中詳細地介紹了德國數學展展覽的動機、展覽的形式、2008—2013年展覽概況、歷史展覽的內容回顧、數學展與中國及在中國展覽的內容與展覽的圖片．同時他也向大家詳細地介紹Surfer、Monament、Cinderella、3Dexploer等軟件．最后，他提出4點思考：科學研究與科學普及相結合；數學美與數學文化的大眾化；融合數學美學到教學中，改變數學的形象；大學與中學的銜接與交流，與社區科普的結合．

《數學文化》是國內很多學校所開設的公共選修課之一．郭運瑞教授在報告中介紹了河南科技學院數學文化課程的教學及其實踐活動的情況，實踐教學活動內容豐富，精彩紛呈，教學活動很有特色，活動中師生積極性之高，學生參與人數之多，影響面之大，輻射范圍之廣，在河南省高校中具有較大的影響，并于2014年該課程被評為省級精品視頻公開課程．

2.8 數學教育

民國時期，是中外數學交流頻繁和中國數學家成果較多的時期，對中國近現代數學的發展影響很大．張紅教授在報告中主要闡述的內容為：數學教育在四川的制度化過程、抗戰前后四川高等院校數學的發展．她通過擷取民國這樣的時間片段，將西方數學對中國近現代數學發展的影響，置于四川這樣的地理環境進行研究，豐富了中國近現代數學以及數學文化傳播的研究．

3 結 語

文化是民族的血脈．數學對于人類的發展、科學的進步、人類的文明等有著重要的意義，它本身就是一種文化．從這次會議報告中，可以感知，中國數學文化研究景象繁榮．“第四屆全國數學文化論壇會議”突出了近年中國數學文化研究與傳播的同時，并直接或間接地提出了今后研究的新課題．

Research and Communication of M athematical Culture——Summary of the Fourth National Academ ic Conference on M athematical Culture

LI Chun-lan
(College of Mathematics Science, Inner Mongolia Normal University, Inner Mongolia Hohhot 010022, China)

In the Fourth National Academic Conference on Mathematical Culture, there are 3 academicians and 15 scholars to make reports, the number of 45 m inutes＇and 25 m inutes’ reports are both 9. The content of every report is rich, the thought is profound. These reports reflect the research and spread of mathematical culture from different areas in recent years in China. Discussion topics include types and characteristics of mathematical culture, the application of mathematics, Chinese traditional mathematics and Chinese culture, the history of mathematics, mathematics and game, the beauty of mathematics, the philosophy of mathematics, the spread of mathematical culture, mathematics education.

the fourth national academic conference on mathematical culture; mathematical culture; the application of mathematics; the history of mathematics; the philosophy of mathematics

G40-055

：A

：1004–9894（2015）01–0091–03

[責任編校：周學智]

2014–11–05

內蒙古師范大學高層次人才科研啟動經費項目——民國時期中學數學教育發展史研究（YJRC12004）；內蒙古師范大學科研

——中國百年小學數學教育研究史（1902—2002）（2012RWZD004）

李春蘭（1978—），女，黑龍江肇源人，副教授，博士，主要從事數學教育與數學史研究．