撓性航天器軌控期間姿態容錯控制

楊婧,　侯建文,　史小平

(1.哈爾濱工業大學 控制與仿真中心,黑龍江 哈爾濱 150080;2.上海航天技術研究院 上海 201109)

?

撓性航天器軌控期間姿態容錯控制

楊婧1,侯建文2,史小平1

(1.哈爾濱工業大學 控制與仿真中心,黑龍江 哈爾濱 150080;2.上海航天技術研究院 上海 201109)

摘要:軌道調控期間,軌道控制推力會對撓性航天器的質心運動與姿態運動產生影響。針對軌道控制期間撓性航天器姿態控制系統的執行機構故障問題,提出了一種基于擴張狀態觀測器(extended state observer, ESO)的滑模容錯控制算法。該算法將執行器故障,系統干擾及參數攝動量視為未知動態,通過設計相應的擴張狀態觀測器,能有效的實現對滑模狀態量及未知動態的估計;在此基礎上,利用未知動態的估計信息,設計了滑模容錯控制控制律。最后,針對軌控期間反作用飛輪故障的撓性航天器姿態系統進行了仿真研究,仿真結果表明該算法能夠有效處理執行器故障并使閉環系統穩定。

關鍵詞:擴張狀態觀測器; 滑模容錯控制; 撓性航天器; 執行器故障

侯建文(1960—)，男，研究員，博士生導師，研究方向為航天器控制；

史小平(1965—)，男，博士，教授，博士生導師，研究方向為飛行器智能控制、復雜系統仿真。

0引言

在軌航天器的工作任務復雜,工作環境惡劣,反作用飛輪作為航天器姿態控制系統的執行機構,其作用重大,一旦飛輪出現故障,姿態控制系統將無法正常工作甚至會造成一系列安全問題;此外,由于受到工作環境及研發成本的制約,使得硬件冗余在解決執行器故障問題方面的應用受限[1]。因此,為了提高航天器姿態控制系統的安全性和可靠性,并降低系統對硬件的依賴,亟需設計相應的容錯控制策略,以保證航天器順利完成工作任務。

容錯控制的主要目的是在系統故障條件下,保證系統的穩定性并盡可能保證系統性能,主要分為被動容錯控制和主動容錯控制兩大類[1]。在航天空之領域,關于星體容錯控制的研究成果相當豐富[2-4]。其中被動容錯控制由于實時性強,不需要故障診斷信息,魯棒性好,控制器形式固定等優點而受到廣泛關注,包括:變結構容錯控制方法[6-7],反推容錯控制理論[8],滑模容錯控制算法[9-10]等。

撓性航天器在軌運行時,不僅會受到環境干擾力矩的影響,撓性附件的振動也會對姿態控制的精度產生影響。目前關于撓性航天器姿態控制已有眾多研究成果[11-12],但對于軌道調控期間的撓性航天器研究成果則較少。進行軌道調控期間的撓性航天器,由于軌道控制推力會激起星體上撓性附件的振動,進而對航天器的質心運動與姿態運動產生影響,其中文獻[13-14]給出了含軌道推力影響的撓性航天器姿態系統動力學模型。考慮到軌道推力控制期間撓性航天器所受到的擾動力矩已遠大于其他運行階段的擾動力矩[11-12],因此在設計容錯控制及主動振動抑制策略時有必要將軌道推力的影響考慮進去。

擴張狀態觀測器具有良好的觀測性能,它不僅能觀測不確定對象的狀態變量,并且能觀測對象模型中內擾和外擾的實時控制量[15]。本文針對軌道控制期間反作用飛輪失效的撓性航天器姿態系統控制問題,在采用了飛輪冗余配置的條件下,基于擴張狀態觀測器理論設計了一種對故障不敏感的滑模容錯控制器,該觀測器能有效的估計執行器故障,外界干擾及系統參數攝動量。最后,將該方法用到含飛輪故障的撓性航天器姿態系統上,仿真結果表明能實現未知動態的精確估計并保證系統的穩定性。

1數學模型

1.1　系統動力學模型

當航天器進行軌道調整時,軌道推力會引起航天器撓性附件的振動,從而對航天器的質心運動與姿態運動產生影響,并引起航天器軌道與姿態運動的耦合[13]。撓性航天器軌道控制期間的系統動力學模型可表示為[1-2]

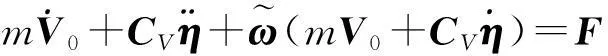
(1)

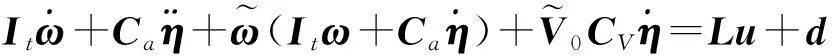
(2)

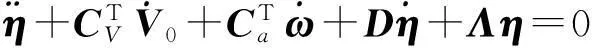
(3)

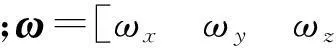
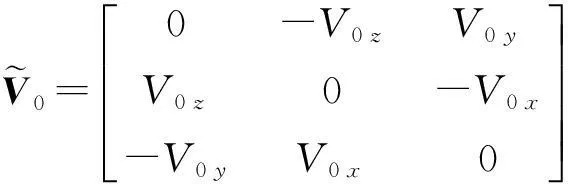
1.2　航天器運動學模型

姿態四元數描述的航天器姿態運動學方程可表示為

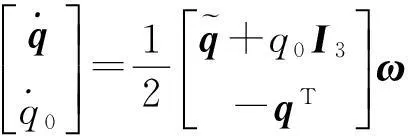
(4)

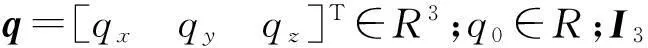
1.3　含執行器故障的姿態系統模型

考慮到航天器的轉動慣量無法精確獲得,不妨將其表示成以下形式

It=It0+ΔIt,

(5)

其中:It0表示轉動慣量的標稱值;ΔIt表示攝動值。

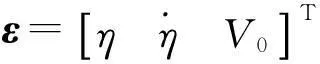
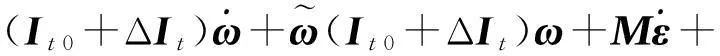
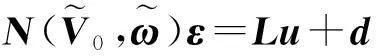
(6)

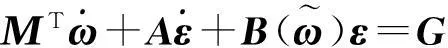
(7)

其中:

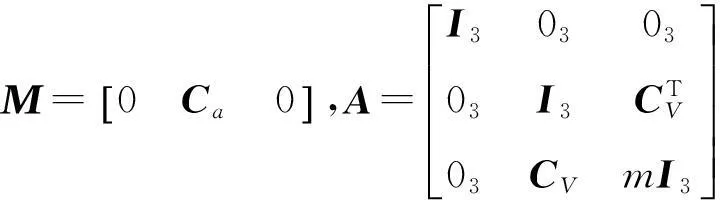
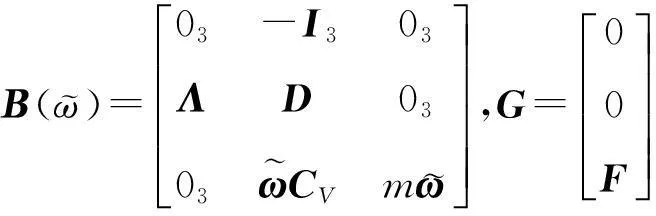
由式(7)可知

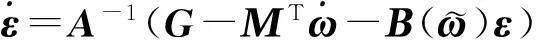
(8)

將式(6)帶入式(8)得

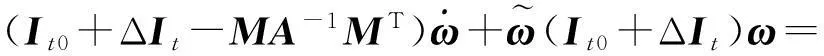
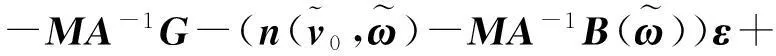
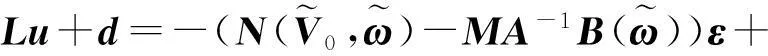
RF+Lu+d,

(9)

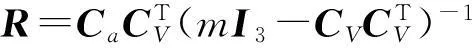
在考慮執行器故障的條件下,式(9)可表示成

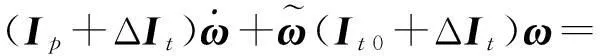
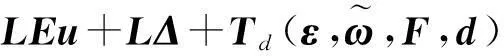
(10)

其中

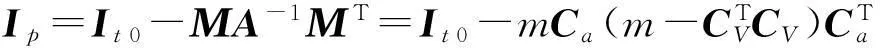
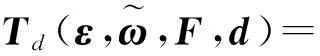
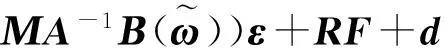
Δ=diag(Δ1,Δ2,Δ3,Δ4)表示恒值偏差故障,E=diag(e1,e2,e3,e4)表示執行器的故障矩陣,ej表示失效因子且滿足

進一步,式(10)可改寫成式(11)

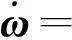
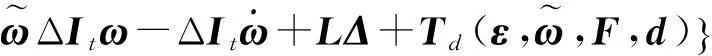
(11)

定義未知動態

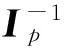
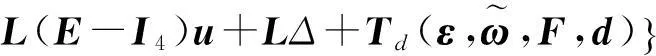
(12)

由式(11)及式(12)可知

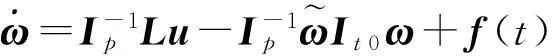
(13)

1.4　問題描述

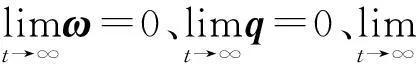
2容錯控制器設計

為了使姿態角及姿態角速度鎮定到期望值,選取滑模變量如下

σ=ω+βq,

(14)

其中β>0。

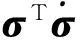
由式(14)可知

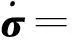
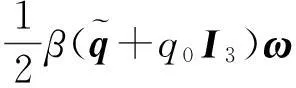
(15)

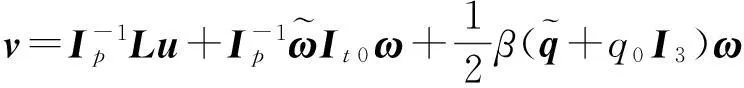
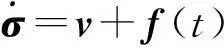
(16)

v=-κ1σ-κ2sgn(σ)-f(t),

(17)

其中k1>0、k2>0為正常數。

注:考慮到故障情形下執行機構的有效控制部分為L(E-I4)u,而容錯控制的前提為系統可控,因此,本文所考慮的執行器故障情形均滿足系統可控條件。

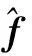
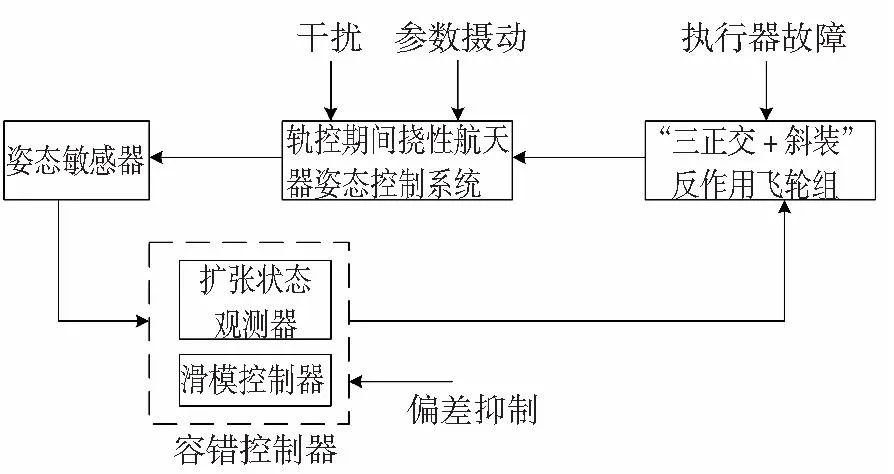
圖1　閉環姿態系統結構框圖

2.1　基于ESO的未知動態估計

由式(16)可知,式(16)可以解耦成以下三個方程組

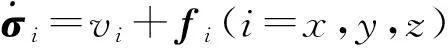
(18)

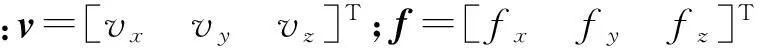
根據式(18),可構造如式(19)的二階擴張狀態觀測器

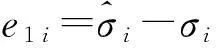
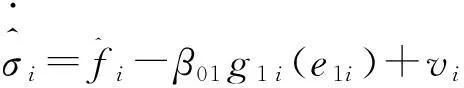
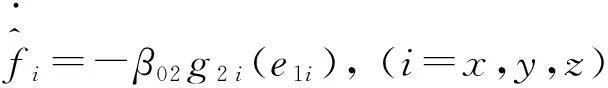
(19)

其中β01、β02為觀測器系數;g1i(e1i)、g2i(e1i)表示具有相應結構的非線性函數。

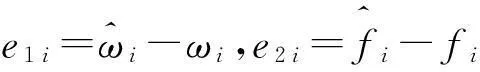
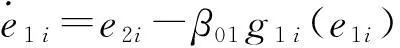
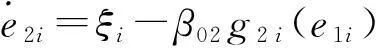
(20)

根據擴張狀態觀測器的收斂性理論可知:當函數滿足條件

g1i(e1i)=e1i，

(21)

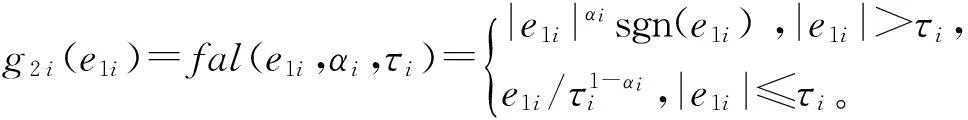
(22)

其中參數0<αi<1,τi>0,并且觀測器系數β01、β02取適當值時,則狀態估計誤差有界收斂,并最終達到以下穩態

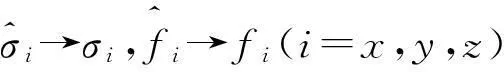
(23)

2.2　滑模容錯控制

根據式(23)及式(17)的分析可知控制律v可選取為

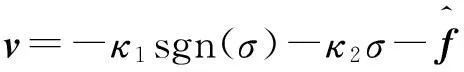
(24)

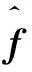
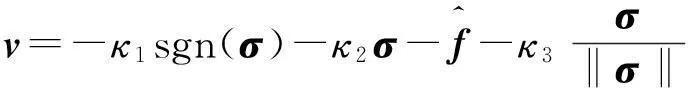
(25)

其中κ1、κ2、κ3>0為正常數。

當控制量v滿足式(25)時,系統的容錯控制律可表示為

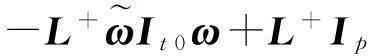
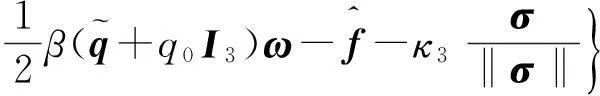
(26)

其中L+表示L的偽逆矩陣,并且滿足L+=LT(LLT)-1。

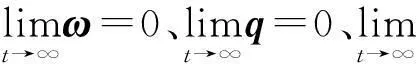
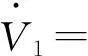
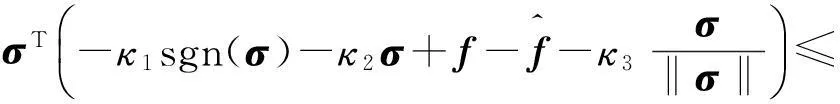
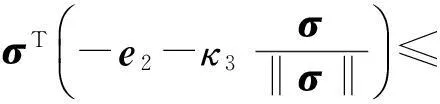
(27)

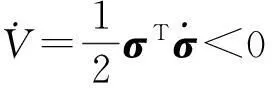
3仿真研究

為了驗證本文控制方法的有效性,本文對軌道控制期間,反作用飛輪故障條件下的撓性航天器姿態控制系統進行了仿真研究,控制參數選取如下:參數攝動量為20%,m=400 kg,ω(0)=[0.001-0.001 20.001 5]Trad/s,F=[111]TN,ωn=diag([0.77

1.11.88],Γ=diag([-0.023 40.004 22-0.003 9]),ε=diag([0.005 70.008 70.013]),q(0)=[0.250.470.53-0.660 1]T,

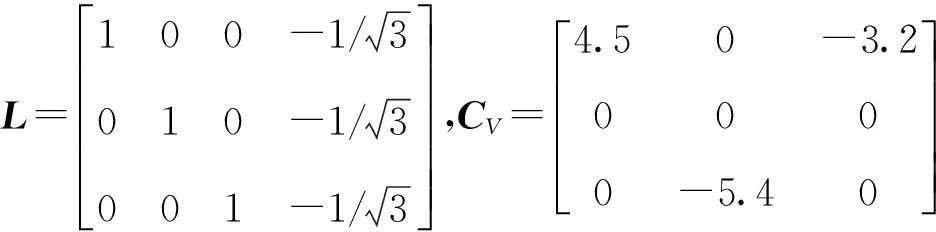
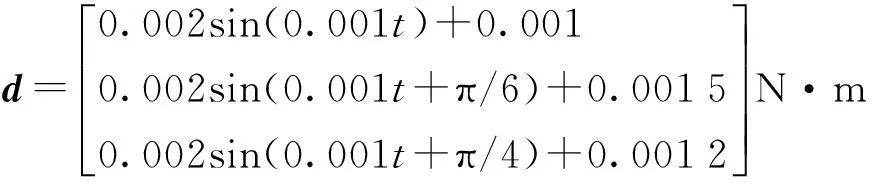
本文選取了執行器乘性故障和加性故障這兩種故障類型,故障參數設置如下:

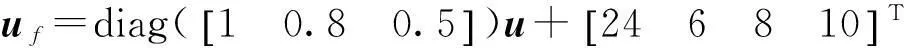
利用Simulink仿真軟件,反作用飛輪故障條件下的控制效果如圖2~圖5所示。

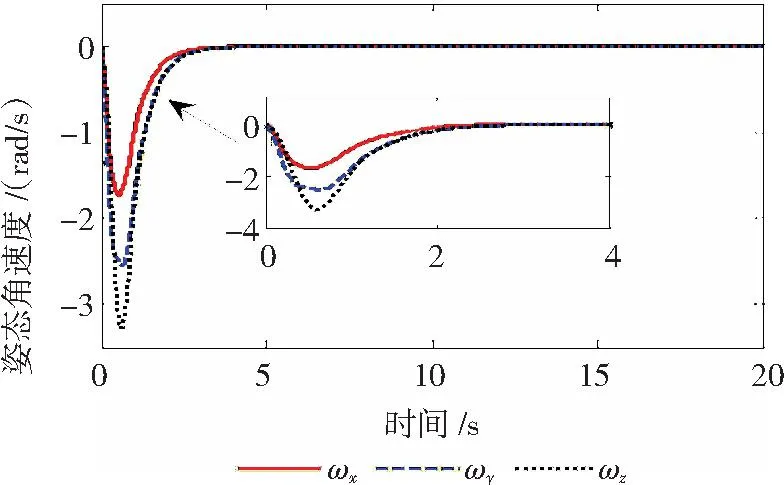
圖2　姿態角速度響應曲線

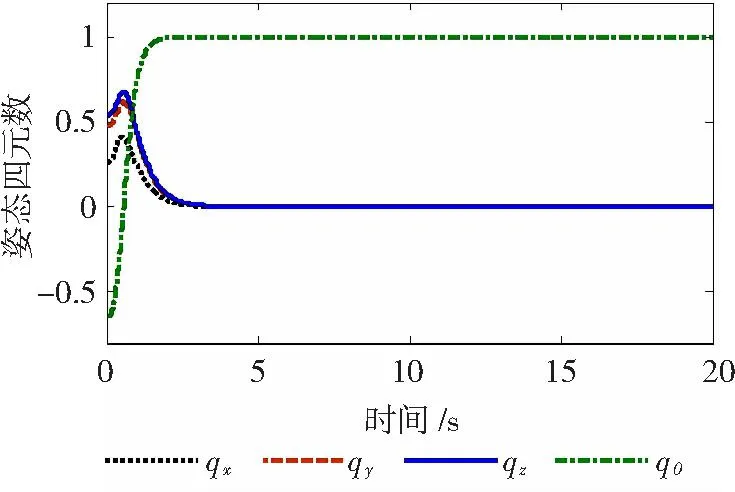
圖3　姿態四元數響應曲線

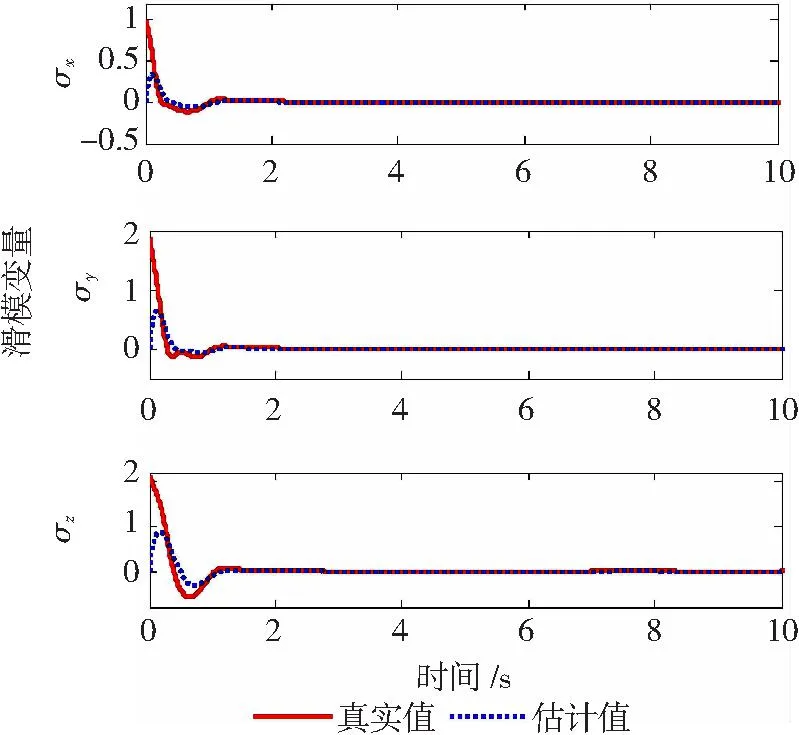
圖4　滑模變量響應曲線

從圖2和圖3中可以看出,在本文所設計的容錯控制器作用下,對執行機構同時出現故障狀況:反作用飛輪1存在24 N·m的恒值偏差故障,反作用飛輪2損失20%控制能力并且存在6 N·m的恒值偏差故障,反作用飛輪3損失50%控制能力并且存在8 N·m的恒值偏差故障,反作用飛輪4完全失去控制能力并且存在10 N·m的恒值偏差故障,撓性航天器姿態控制系統能迅速穩定,并且姿態角及姿態角速度矢量均能收斂到期望值。

從圖4和圖5可以看出,在容錯控制器的作用下,擴張狀態觀測器能夠有效的觀測滑模變量及未知動態的變化,具有良好的觀測效果。

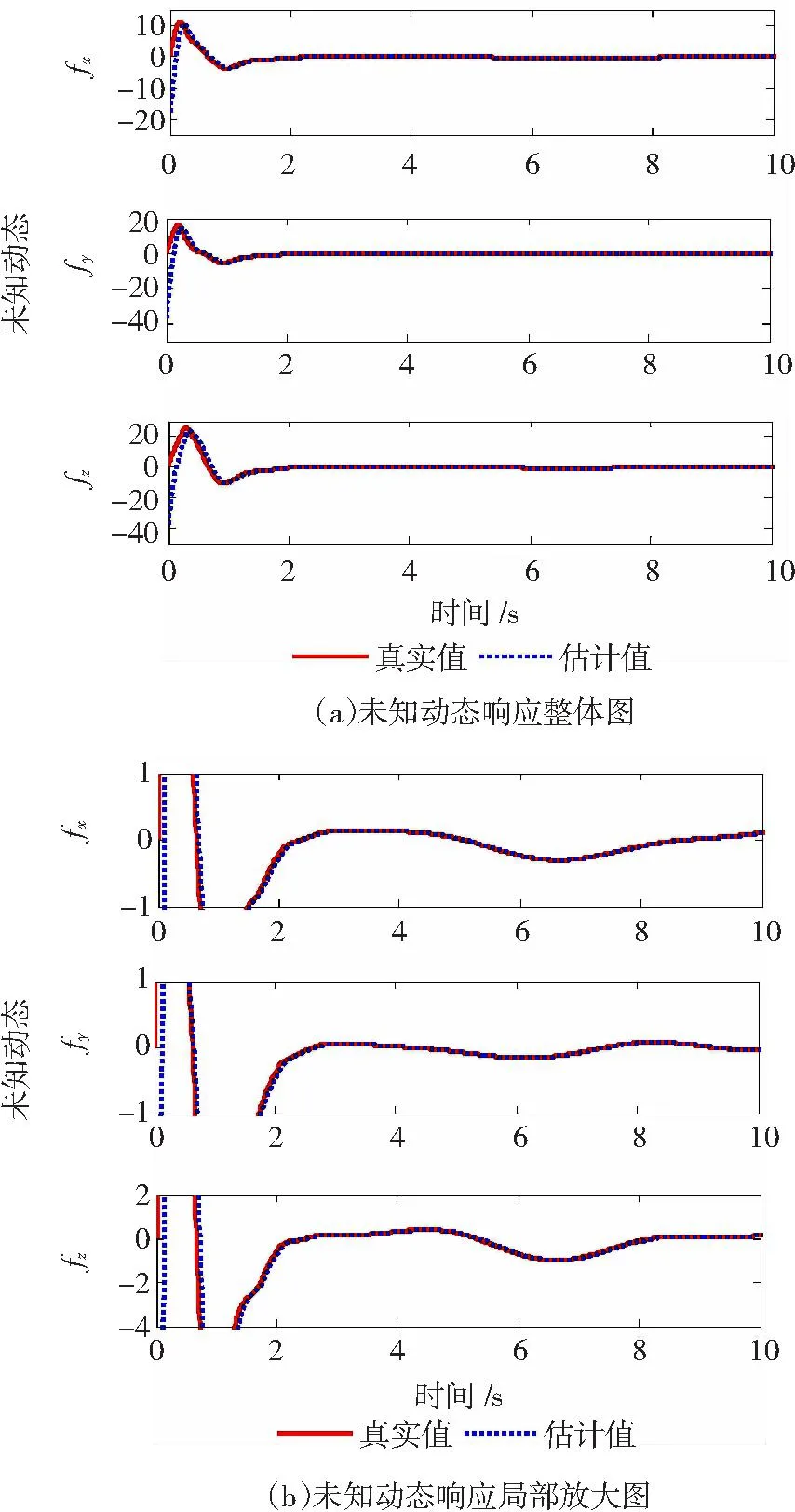
圖5　未知動態響應曲線

4結論

針對軌道調控期間的撓性航天器姿態系統,研究了姿態控制系統反作用飛輪故障下的容錯控制問題。本文將執行器故障、系統不確定性及系統內部和外部干擾視為未知動態,通過設計擴張狀態觀測器,能有效地估計滑模變量及未知態;在此基礎上,結合未知動態的估計值,設計了一種對反作用飛輪故障不敏感的滑模容錯控制器。仿真結果表明,該容錯控制算法不僅具有良好的容錯控制效果,還能有效地觀測滑模變量及未知動態的變化。

參 考 文 獻:

[1]張愛華,胡慶雷,霍星,等. 過驅動航天器飛輪故障重構與姿態容錯控制[J]. 宇航學報, 2013, 34(3): 369-375.

ZHANG Aihua, HU Qinglei, HUO Xing, et al. Fault reconstruction and fault tolerant attitude control for over-activated spacecraft under reaction wheel failure[J].Journal of Astronautics, 2013,34(3):369-375.

[2]姜野. 控制受限的撓性航天器姿態容錯控制[D]. 哈爾濱:哈爾濱工業大學, 2011.

[3]張嫻,程月華,姜斌.軌控期間撓性航天器姿控系統的容錯控制[J].航天控制, 2011, 29 (1): 41-47.

ZHANGXian, CHENG Yuehua, JIANG Bin. Adaptive backstepping fault-tolerant control for flexible spacecraft attitude control system during orbit control [J]. Aerospace Control, 2011, 29(1): 41-47.

[4]閆鑫. 基于滑模的航天器執行機構故障診斷與容錯控制研究[D]. 哈爾濱:哈爾濱工程大學自動化學院,2014:10-12.

[5]霍星, 胡慶雷, 肖冰,等. 帶有飽和受限的撓性航天器變結構姿態容錯控制[J].控制理論與應用,2011,28(9):1063-1068.

HUO Xing, HU Qinglei, XIAO Bing, et al. Variable-structure fault-tolerant attitude control for flexible spacecraft with input saturation[J].Control Theory & Applications, 2011,28(9): 1063-1068.

[6]姜野, 胡慶雷, 馬廣富. 航天器時延自適應變結構容錯控制[J].控制與決策, 2010, 25(5): 651-656.

JIANG Ye, HU Qinglei, MA Guangfu. Combined adaptive variable structure and time delay fault tolerant control for spacecraft[J]. Control and Decision, 2010, 25(5): 651-656.

[7]胡慶雷,張愛華,李波.推力器故障的剛體航天器自適應變結構容錯控制[J].航空學報, 2013, 34(4): 909-918.

HU Qinglei, ZHANG Aihua, LI Bo. Adaptive variable structure fault tolerant control of rigid spacecraft under thruster faults[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(4):909-918.

[8]ALI I, RADICE G, KIM J. Backstepping control design with actuator torque bound for spacecraft attitude maneuver [J]. Journal of Guidance Control and Dynamics, 2010, 33(1): 254-259.

[9]程月華,姜斌,孫俊,等.基于滑模觀測器的航天器姿態控制系統滑模容錯控制[J]. 上海交通大學學報,2011,45(02): 190-194.

CHENG Yuehua,JIANG Bin,SUN Jun,et al. Sliding mode fault tolerant control for spacecraft attitude systems based on sliding mode observer[J].Journal of Shanghai Jiaotong University, 2011,45(02): 190-194.

[10]肖冰,胡慶雷, 霍星,等. 執行器故障的撓性航天器姿態滑模容錯控制[J].航空學報, 2011,32(10): 1869-1878.

XIAO Bing, HU Qinglei, HUO Xing, et al. Sliding mode fault tolerant attitude control for flexible spacecraft under actuator fault[J], Acta Aeronautica et Astronautica Sinica, 2011,32(10): 1869-1878.

[11]朱良寬, 馬廣富, 胡慶雷. 撓性航天器魯棒反步自適應姿態機動及主動振動抑制[J]. 振動與沖擊, 2009, 28(2): 132-136.

ZHU Liangkuan, MA Guangfu, HU Qinglei. Attitude maneuvering and vibration damping of flexible spacecraft via robust adaptive backstepping technique [J]. Journal of Vibration and Shock, 2009, 28(2): 132-136.

[12]HU Qinglei, MA Guangfu. Variable structure control and active vibration suppression of flexible spacecraft during attitude maneuver [J], Aerospace Science and Technology, 2005, 90: 307-317.

[13]劉瑩瑩, 周軍. 航天器軌道控制力對撓性帆板振動的影響[J]. 西北工業大學學報, 2009, 27(1): 61-65.

LIU Yingying, ZHOU Jun. Influence of spacecraft control force on its flexible solar panel during orbit maneuver[J]. Journal of Northwestern Polytechnical University, 2009, 27(1): 61-65.

[14]LIU Yingying, ZHOU Jun. Fuzzy attitude control for flexible spacecraft during orbit maneuver[C]//IEEE 6th International Conference on Mechatronics and Automation, August 9-12, 2009, Changchun, China. 2009:9-12.

[15]夏長亮,劉均華,俞衛,等. 基于擴張狀態觀測器的永磁無刷直流電機滑模變結構控制[J]. 中國電機工程學報,2006,26(20):139-143.

XIA Changliang, LIU Junhua, YU Wei, et al. Variable structure control of BLDCM based on extended state observer[J]. Proceedings of the CSEE, 2006, 26(20):139-143.

(編輯：張詩閣)

Fault tolerant attitude control of flexible spacecraft during orbit control

YANG Jing1,HOU Jian-wen2,SHI Xiao-ping1

(1.Control and Simulation Center, Harbin Institute of Technology, Harbin 150080, China;

2. Shanghai Academy of Spaceflight Technology, Shanghai 201109, China)

Abstract:The orbit control force would generate disturb torque which has impacts on the centroid and attitude motion of flexible spacecraft during spacecraft orbit maneuver. A sliding mode fault tolerant control approach was proposed based on an extended state observer (ESO) for the flexible spacecraft attitude control system with actuator faults during orbit control. In this approach, unknown actuator faults, internal and external disturbance, and parameter perturbation are considered as unknown dynamics. Based on the ESO design approach, sliding mode and unknown dynamics were effectively estimated, and sliding mode fault tolerant control approach was designed by using the estimating information. At last, the simulation results of flexible spacecraft were presented to demonstrate the effective of this approach.

Keywords:extended state observer; sliding mode fault tolerant control; flexible spacecraft; actuator faults

通訊作者:楊婧

作者簡介:楊婧(1989—)，女，博士研究生，研究方向為飛行器控制，容錯控制；

基金項目：武器裝備預研基金(9140A20040515HT01001)

收稿日期:2014-07-20

中圖分類號:TP 302.8

文獻標志碼:A

文章編號:1007-449X(2015)07-0111-06

DOI:10.15938/j.emc.2015.07.017